一种非线性因子的粘性二进制粒子群算法

摘  要：为了解决粘性二进制粒子群算法在优化过程中易陷入局部最优、全局搜索能力弱、后期收敛性能差的弊端，提出了一种非线性因子的粘性二进制粒子群算法（NFSBPSO）。NFSBPSO算法采用非线性递减策略优化粘性权重，平衡全局与局部探索能力；同时，利用混沌策略对种群进行初始化，在每个迭代过程中对最差和最优粒子进行优化，以提高种群质量，扩大种群的全局探索能力。将新算法与3个对比算法在基准函数上进行测试，实验表明新的算法能较好地跳出局部最优，提高了算法的稳定性和收敛能力。

关键词：非线性因子；混沌策略；粒子优化；粘性二进制粒子群算法

中图分类号：TP301  文献标识码：A  文章编号：2096-4706（2023）03-0061-05

A Nonlinear Factor Sticky Binary Particle Swarm Optimization

CHENG Qianqian

（Taiyuan Normal University， Jinzhong  030619， China）

Abstract： In order to solve the disadvantages of sticky binary particle swarm optimization， which is easy to fall into local optimum， weak global search ability and poor late convergence performance in the process of optimization， a nonlinear factor sticky binary particle swarm optimization （NFSBPSO） is proposed. NFSBPSO algorithm uses nonlinear decreasing strategy to optimize the sticky weight and balance the global and local exploration ability. At the same time， the chaos strategy is used to initialize the population， and the worst and best particles are optimized in each iteration process to improve the quality of the population and expand the global exploration ability of the population. The new algorithm is tested on the benchmark function with three comparison algorithms. The experimental results show that the new algorithm can jump out of the local optimum better and improve the stability and convergence ability of the algorithm.

Keywords： nonlinear factor; chaos strategy; particle optimization; sticky binary particle swarm optimization

0  引  言

Kennedy等人于1995年提出的粒子群算法（Particle Swarm Optimization， PSO）[1]作为群智能优化算法，因其具有参数少、运算简单和收敛速度快等特点受到广大学者的关注，此算法多用来处理连续函数的优化。针对离散域上存在的问题，Kennedy等人于1997年进一步提出了二进制粒子群算法（Binary Particle Swarm Optimization， BPSO）[2]。BPSO算法与PSO算法相比，尽管全局搜索能力较强，但是仍不能很好地收敛到全局最优位置，并且算法的随机性随着迭代次数的渐增而增大，局部搜索能力越来越弱[3，4]。2019年Nguyen等人所发表的粘性二进制粒子群算法（Stickiness Binary Particle Swarm Optimization， SBPSO）[5]，采用了粘性和翻转的思想，使算法更适用于离散问题，寻优的效果更佳。与粒子群算法相似，这些离散粒子群优化算法也存在早熟收敛问题[6-8]，相關学者针对这一问题提出了改进策略。李真等人[9]提出将灰狼算法与粒子群算法相结合，增加了粒子的收敛速度；李浩君等人[10]提出惯性权重和种群多样性协同调整的策略，增强了算法的动态搜索的能力和种群多样性；孙一凡等人[11]提出了一种粒度散度指标，并将模拟退火机制与粘性二进制粒子群算法相结合，平衡了算法的探索和开发能力；王皓等人[12]提出了对粒子进行邻域搜索和扰动，加快了收敛速度。邱飞岳等人[13]利用混沌策略和成长因子来均衡全局与局部搜索的能力。王越等人[14]提出对惯性权重采用一种非线性递增的方法，将变异算子加入速度公式中，增强了粒子的种群多样性和寻优范围。

虽然上述研究通过不同的策略对粒子群算法进行了优化，但在处理离散问题时，算法的性能还需要进一步的提升。本文从算法易陷入局部最优，探索和开发能力不平衡的问题出发，利用Logistic混沌策略初始化种群，采用非线性的策略改变粘性权重，并且对进化过程中对最差和最优粒子进行优化，提出了一种非线性因子的粘性二进制粒子群算法（Nonlinear Factor Stickiness Binary Particle Swarm Optimization， NFSBPSO）。

1  粘性二进制粒子群算法

1.1  二进制粒子群算法

传统的二进制粒子群算法（BPSO）与粒子群算法（PSO）所用的速度更新公式一样，而BPSO算法将映射函数应用到位置公式上，也就是说将粒子的速度映射到[0，1]区间，如果映射值小于随机数，则位置取0，反之取1。PSO算法应用在连续域的问题上，而BPSO算法应用于处理离散域的问题。式（1）为速度更新公式，式（2）为映射函数，式（3）为位置更新公式：

（1）

（2）

（3）

其中，j为维度，vij （t+1）为粒子i在t+1次迭代的速度，w为惯性权重，c1和c2分别为自我和社会学习因子，r1和r2为[0，1]中的随机变量，xij （t）为第i个粒子的当前位置；pbestij为个体历史最优解，gbestij为全局最优解；T（vij （t））為映射函数，表示速度映射的概率值。

为了使PSO算法可以解决离散问题，因此引入了映射函数，但在离散问题中直接使用PSO的速度和位置公式并不能直观的描述离散空间的速度和位置，因此有学者提出了粘性二进制粒子群算法。

1.2  粘性二进制粒子群算法

粘性二进制粒子群算法（SBPSO）可以更加精准地描述粒子的运动状态，即粒子的翻转代替为粒子运动，粒子的翻转速率则为粒子的运动速率。粘性是指在离散域中，粒子运动维持当前比特位不变的概率值。该算法在解决离散问题中效果比BPSO算法有一定的提升。速度和位置更新公式如式（4）（5）所示。

（4）

（5）

其中，xij（t）的值为0或1，is为粘性权重，stkij（t）为第i个粒子的粘性，也就是说当粒子刚发生翻转后，stkij（t）值为1，并使该粒子保持一段时间的平衡，但粘性值会随着迭代次数的增加而不断衰减，直至再次翻转或者粘性为0。SBPSO算法采用式（6）动态参数控制策略来平衡算法的探索和开发能力，相关参数如式（7）～（9）所示：

（6）

（7）

（8）

（9）

（10）

其中，is+ip+ig=1，，is_u和is_l分别为粘性权重is的上限和下限，t为当前迭代次数，T为最大迭代次数；ustk为粒子的粘性值从1衰减到0所需的迭代次数，ustk_u和ustk_l分别为ustk的上限和下限。

通过实验发现该算法在一定条件下容易陷入局部最优。当粒子处于全局最优的位置时，翻转概率仅由动量和粘性衰减决定，通过大量的迭代使得粘性衰减来获得翻转概率，这不仅耽误了算法寻优的进程，而且不利于实现算法探索与开发之间的平衡。该算法在大型和复杂的搜索空间上表现良好，但在小型的搜索空间上寻优效果并没有显著提升，因此，需要对参数进行非线性的更新机制。

2  非线性因子粘性二进制粒子群算法

2.1  非线性因子is

粘性权重is的大小影响着算法的探索和开发的能力。当is的值较大时，提高了粒子的翻转概率，有利于探索；当is的值较小时，降低了粒子的翻转概率，有利于开发，避免陷入局部最优。对于粘性权重is来说，线性递减不能有效的解决所有的寻优问题，当问题较为复杂时，局部搜索能力逐渐降低，找不到所要求的最优解。

SBPSO算法采用的典型的线性递减的策略来改变粘性权重的值。但因为其斜率保持不变，所以翻转概率的改变速率持续性降低，在迭代初期还没有很好地找到全局最优解便会进入局部搜索，从而使算法陷入局部最优解。因此，采用指数函数  对粘性权重函数进行改进。

但是在  公式中，曲线在最高点维持的时间较短且粘性权重的值在迭代结束后不能收敛到最小值，而当t/T为六次幂且系数为-20时，最高点和最低点维持的时间均衡，有利于平衡前后期探索和开发的能力。

因此，本文提出一个非线性的is因子（Nonlinear Factor， NF），如式（11）所示，以平衡算法的探索和开发能力。非线性is曲线图如图1所示。

（11）

由图1可以看出，当最大迭代次数为200次时，is在前50次迭代过程中能保持在最大值附近，可以更好地进行全局搜索，在后50次迭代过程中能保持在最小值附近，以便于迭代前期全局搜索能力与迭代后期局部搜索能力的良好平衡。

2.2  混沌初始化策略

粘性二进制粒子群算法的初始种群是通过随机策略生成的，其种群分布较差，质量不高。为了提高种群的质量，NFSBPSO算法采用Logistic映射进行混沌初始化，如式（12）所示：

（12）

其中，μ表示混沌程度，μ的值越大，混沌程度越高；实验得出，当μ=4时，系统的混沌状态最佳。在映射过程中，若xt≥0.5，xt=1；若xt＜0.5，xt=0。

2.3  粒子优化策略

SBPSO算法在迭代过程中所有粒子会向最优粒子位置运动，造成种群多样性降低，影响了粒子从局部最优跳出。本文通过借鉴最优粒子扰动策略和最差粒子更新策略来改进NFSBPSO算法，提高算法后期的搜索能力。

2.3.1  最差粒子更新策略

在粒子群算法中，一直秉承着“优胜劣汰”的生存法则，为了提高最差粒子的质量，在迭代过程中其进行更新操作。最差粒子更新策略就是改进种群中适应度最糟糕的粒子，目的是增加种群的多样性，进而提高搜索能力。最差适应度粒子改进公式如式（13）（14）（15）所示：

（13）

（14）

（15）

其中，x_worst表示适应度最糟糕的粒子；式（14）中Eworst表示更新后的粒子，也就是在每次迭代完成后，随机性地选取三个不同的粒子进行更新。式（15）表示，如果更新后粒子的适应度值小于最差粒子，则将最差粒子更新为Eworst；反之保留最差粒子。

2.3.2  最优粒子扰动策略

在SBPSO算法中，种群的全局最优解会影响所有粒子朝着最优解的方向移动，从而导致后期发生聚集现象，所以本文根据种群的聚集程度，对全局最优解的位置进行扰动，从而扩大种群的全局搜索能力。

判断种群聚集程度的公式如式（16）（17）所示：

（16）

（17）

其中，avg_x表示N个粒子的中心位置，avg_r表示种群中N个粒子到avg_x的平均距离。若avg_r值较大，表示粒子分布比较散，种群多样性较强，则对全局最优解产生的干扰较小。若avg_r值较小的话，表示粒子分布比较紧密，导致种群已经陷入局部最优或者多样性降低，则对全局最优解产生的干扰较大。

本文采用的扰动策略如式（18）（19）所示，对全局最优解产生的扰动大小由公式中的指数函数所决定，而上文說明了扰动大小与avg_r呈负相关，因此指数函数与avg_r呈负相关：

（18）

（19）

其中Nbest（t）代表被干扰后的粒子，如果Nbest（t）的适应度值低于被干扰之前的适应度值，则被干扰后的粒子为全局最优粒子；否则不进行更新。

2.4  NFSBPSO算法步骤

本文在粘性二进制粒子群算法的基础上，采取混沌策略、非线性粘性权重以及粒子优化策略，提出了NFSBPSO算法，算法步骤如下：

Step1：采用Logistic混沌策略初始化种群；

Step2：参数初始化；

Step3：计算适应度值，并对种群个体进行历史最优解及全局最优解的更新；

Step4：更新非线性因子is；

Step5：对适应度值最糟糕的粒子进行改进；

Step6：针对粒子的全局最优位置进行扰动，根据扰动后粒子的适应度判断是否需要更换全局最优解；

Step7：更新粒子的速度和位置；

Step8：对算法的终止条件进行判断，如果满足条件就输出最优解；如果不满足，则返回步骤3。

3  仿真实验

3.1  实验环境

实验采用MATLAB语言编程，Window 10操作系统，Intel（R） Core（TM） i5-6200U CPU 处理器，主频为2.40 GHz。

3.2  实验设置

本文选取了六种基准函数来对算法进行了性能测试与评价，如表1所示。F1、F2、F3是单峰函数且只具有一个最优解，可用于判断算法的收敛性能；F4、F5、F6是多峰函数且具有多个局部最优解，可以用来判断算法跳出局部最优解的能力。对比算法为BPSO算法[2]，SBPSO算法[5]，动态自均衡二进制粒子群算法（Dynamic self-equilibrium binary particle swarm optimization， DSEBPSO）[15]。种群规模N=30，最大迭代次数T=200。根据先验经验，粘性值上限 ，下限 ；自适应因子上限 ，下限 。根据文献[5]可知α=2时，寻优效果更佳。

实验采用以下两种标准来评价算法的性能：

（1）均值：4个算法运行30次后，获得最优值的均值。

（2）方差：4个算法运行30次后，获得最优值的方差。

3.3  实验结果分析

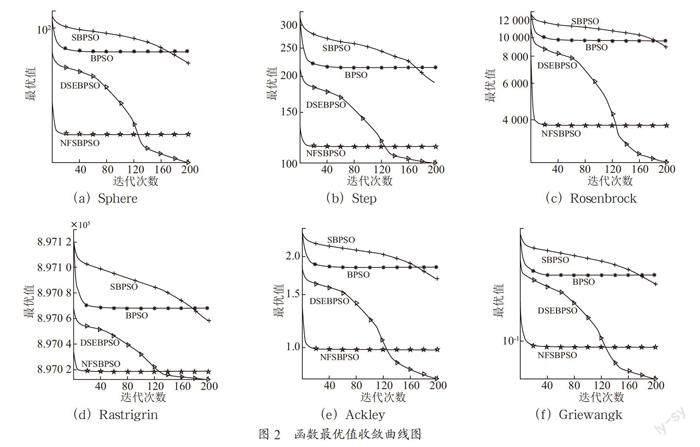
NFSBPSO算法和三个对比算法在六个基准函数上的收敛曲线如图2所示。

由图2可知，NFSBPSO算法在收敛速度、跳出局部最优解等方面都要比其他算法好。由于迭代时粘性权重的非线性调整，使得单峰函数在寻优过程中适应值变化迅速，寻优成功率与收敛精度也显著增加。对于局部最优解较多的多峰函数问题，该算法使用粒子优化策略对适应度值较差的粒子加以改进，以提高其种群的多样性，同时对全局最优粒子加以干扰，促进其跳出局部最优从而使得算法能够做出较好的局部探索。

NFSBPSO算法和三个对比算法在六个基准函数上的实验结果如表2所示。

单峰函数仅有一个局部最优解来检测其收敛精度。从表2中可以看出，在单峰函数F1、F2、F3中，NFSBPSO算法的均值比其他算法好，表明该算法比BPSO、SBPSO以及DSEBPSO算法具有更高的收敛精度。多峰函数具有多个局部最优解来评价算法是否能够跳出局部最优。从表2中可以看出，在多峰函数F4、F5、F6中，NFSBPSO算法的均值明显好于其他算法，表明其具有更强的跳出局部最优解能力。整体来看，NFSBPSO算法的方差在单峰函数和多峰函数中，均优于其余算法，说明算法的稳定性也有了进一步的提升。

4  结  论

本文提出的NFSBPSO算法在参数上采用了非线性策略，使算法在收敛性能上得到了提升。为了均衡算法的探索和开发能力，在迭代过程中使用最差粒子改进策略和最优粒子扰动策略，提高了算法的寻优能力。但在运行过程中发现不断地优化和改进使得算法的时间复杂度较高，需要在以后的工作中研究改进。

参考文献：

[1] KENNEDY J，EBERHART R. Particle swarm optimization [C]//IEEE International Conference on Neural Networks，Perth：IEEE，1995：1942-1948．

[2] KENNEDY J，EBERHART R C. A discrete binary version of the particle swarm algorithm [C]//International conference on Systems.Orlando：IEEE，1997：4104-4108.

[3] 张鹏威.采用正弦映射与扩张算子的二进制粒子群优化算法 [J].小型微型计算机系统，2019，40（6）：1160-1164.

[4] 赵远东，方正华.带有权重函数学习因子的粒子群算法 [J].计算机应用，2013，33（8）：2265-2268.

[5] NGUYEN B H，XUE B，ANDREAE P，et al. A new binary particle swarm optimization approach：momentum and dynamic balance between exploration and exploitation [J].IEEE Transations on Cyberntics，2021，51（2）：589-603.

[6] 姜磊，刘建华，张冬阳，等.一种自适应变异二进制粒子群算法 [J].福建工程学院学报，2020，18（3）：273-279.

[7] PAN A Q ，WANG L，GUO W A. A diversity enhanced multiobjective particle swarm optimization [J].Information Sciences：An International Journal，2018，436-437：441+465.

[8] 徐浩天，季伟东，孙小晴，等.基于正态分布衰减惯性权重的粒子群优化算法 [J].深圳大学学报：理工版，2020，37（2）：208-213.

[9] 李真，王帆，王冉珺.一种结合灰狼算法的粒子群优化算法 [J].计算机测量与控制，2021，29（10）：217-222.

[10] 李浩君，張广，王万良.一种惯性权重与种群多样性协同调整的二进制粒子群优化算法 [J].小型微型计算机系统，2018，39（3）：529-533.

[11] 孙一凡，张纪会.基于模拟退火机制的自适应粘性粒子群算法 [J].控制与决策，1-10[2022-09-03].https：//kns.cnki.net/kcms/detail/detail.aspx？dbcode=CAPJ&dbname=CAPJLAST&filename=KZYC20220512001&uniplatform=NZKPT&v=SFfl7Znyzm7G6kYM3mYnqTigMmGf3EFhaf0-oqT7JD8EXhm3pVm_PJiZON1c2qsz.

[12] 王皓，欧阳海滨，高立群.一种改进的全局粒子群优化算法 [J].控制与决策，2016，31（7）：1161-1168.

[13] 邱飞岳，王京京.自适应学习因子的混沌二进制粒子群优化算法 [J].浙江工业大学学报，2020，48（4）：411-417.

[14] 王越，邱飞岳，郭海东.一种带变异算子的自适应惯性权重二进制粒子群优化算法 [J].小型微型计算机系统，2019，40（4）：733-737.

[15] 李浩君，吴嘉铭，戴海容.基于多维关联本体的学习资源推荐方法 [J].浙江工业大学学报，2021，49（4）：374-383.

作者简介：程倩倩（1997—），女，汉族，山西运城人，硕士研究生在读，研究方向：教育软件开发技术。

收稿日期：2022-09-21