正弦法的压电式力传感器动态特性的研究

王 振,王 军,夏冰玉,王潇瑛,范海艇

(上海市质量监督检验技术研究院,上海 201114)

0 引言

随着激光技术和数据采集及数字信号处理系统等技术的发展,针对动态力的动态特性的研究,相继建立了基于振动台的正弦力校准装置、冲击力校准装置和阶跃力校准装置[1-3]。力传感器的动态校准方法(正弦力法和冲击力法)都需要用到质量块,利用质量块的加速度与质量的乘积来复现力值。质量块质量的测量精度很高,但是传感器端部等效质量的参数识别是影响动态力测量精度的关键因素[4]。在振动冲击情况下,质量块加速度不是均匀分布的,尤其在大力值和高频下,这种不均匀的加速度分布直接影响动态力复现的误差[5]。

因此必须考虑和研究质量块加速度分布和力传感器的端部等效质量对传感器动态特性的影响。通过非接触的激光干涉法测量质量块表面的加速度[6],保证质量块表面加速度测量精度。R.Kumme[7]通过有限元法(FEM)研究了整个质量块体加速度的修正理论。王宇等[8]在其基础上提出了并经有限元计算验证降低质量块振动响应不均匀影响的设计方案。鉴于传感器增加附加质量对传感器动态特性的重要影响[9]。通过两次配重或多次配重拟合消去法进行实验,得到端部等效质量,由试验可知端部等效质量随频率的变化,另外端部等效质量还与安装有关,在相同的频率点上每次重新安装后系统的附加质量会有轻微差异,但在系统为线性的状态下,这种差异不会影响最终校准结果[10-11]。江文松等[12]通过建立参数化数学模型对被校准力传感器的结构特征进行研究,实现了以较小的标准差辨识被校准力传感器的结构参数。

本文将对压电式力传感器建立基于正弦法的数学模型,从频域方面研究传感器端部等效质量对传感器灵敏度校准的影响,并研究压电式力传感器有效使用频率范围内的灵敏度随系统频响特性的变化。

1 压电式力传感器校准的数学模型的建立

待校准的力传感器与附加质量块通过螺纹连接固定于振动台面上,通过标准振动台对动态力传感器进行正弦激励,激光干涉仪测量附加质量块表面中心的加速度。如图1所示,假设质量块为刚体,而且刚性螺纹连接,则可认为整个质量块各处加速度都与表面中心处加速度相等。

图1 正弦力法校准结构简图

根据惯性力F=m0a,其中m0=m1+m2,m1为附加质量块质量,m2为传感器与质量块之间联接机构的质量,a为测得的质量块上表面中心的加速度。高速同步采集仪选用LAN-XI 数据采集前端和PULSE 系统。适调仪选用Kistler的5018型电荷放大器,被测传感器选用Kistler的9321型压电式力传感器,如图2。

图2 Kistler 9321型压电式力传感器

在电荷放大器上先设置出厂给出的参考灵敏度-3.666 pC/N。选用的附加质量块均为高度与直径比约为2的圆柱体。选择80 Hz作为参考频率,控制力峰值在约200 N量级范围,依次在4个质量块下测试(保证每次螺纹连接的扭矩相同),频谱分析试验图像如图3所示,数据列表见表1。

表1 压电式力传感器灵敏度校准结果(未考虑传感器端部等效质量)

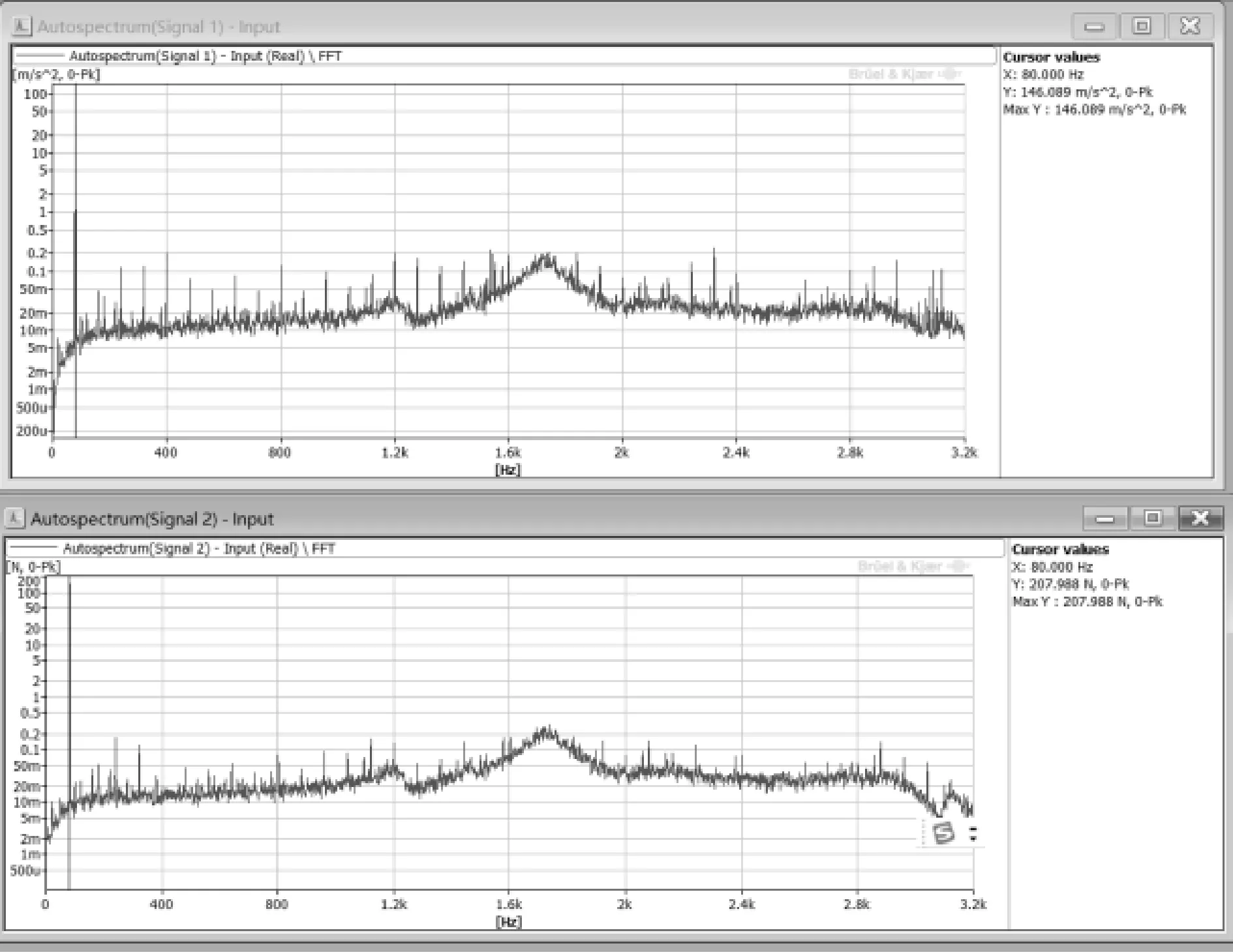
图3 力传感器输出和质量块中心加速度频谱图

分析表1可得:

(1)理论上通过4个不同质量块测得的灵敏度应该是几乎相等的,但是所得的传感器灵敏度都比出厂给定的参考灵敏度大。

(2)质量块质量越小偏差越大,随之质量增加,慢慢趋向于出厂给定的参考灵敏度。因此可以推断力传感器端部有部分质量引入的惯性力没有考虑。

(3)通过图4可知当附加质量块大约在11 kg左右时,即传感器质量的120倍时,可不考虑端部质量引入的惯性力影响。但质量块小时,必须考虑端部质量引入的惯性力对灵敏度的影响,此时惯性力修正为

图4 灵敏度随附加质量变化图

F=(m0+mb)a

(1)

式中mb为传感器端部等效质量。

一般压电式动态力传感器内部简化模型是由上下质量块组成的单自由度体系,当被测系统质量与振动台面质量相比很小时,可以将这种激振视为支撑运动式激振,当被测振动体的质量与振动台面的质量相近时,必须考虑台面质量对被测系统的影响[13],其受力分析如图5所示。其中m0可通过天平测量。mb为压电式力传感器等效顶部质量,mt为压电式力传感器等效底部质量,Fk为压电式传感器内部弹性力,Fc为阻尼力。

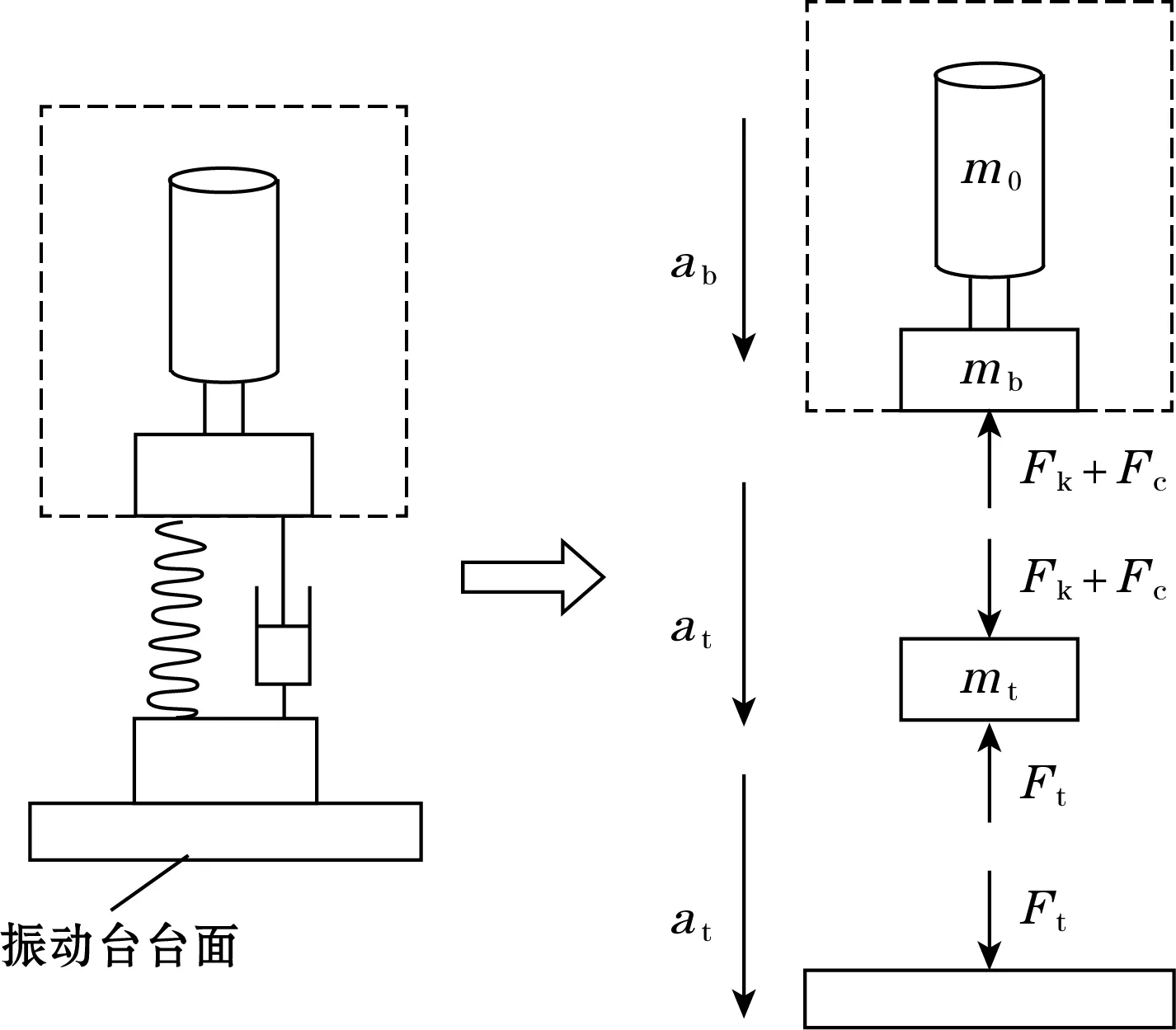
图5 正弦法力传感器受力示意图

由于正弦力的激励,各部分质量将产生惯性力。假设附加质量块、连接机构和压电式力传感器顶部等效质量作为一个刚性整体,根据达朗贝尔原理,建立动平衡方程为:

(m0+mb)ab+Fk+Fc=0

(2)

mtat-Fk-Fc+Ft=0

(3)

整理式(2)、式(3)得:

Fk=-(m0+mb)ab-Fc

(4)

Ft=Fk+Fc-mtat

(5)

通过式(4)分析由于振动系统有持续的正弦激励提供能量,振动的幅值不衰减,因此可以不考虑阻尼力Fc的影响,因此式(4)变为

Fk=-(m0+mb)ab

(6)

因为假设为整体刚性,所以附加质量块上表面的加速度a=ab,在电荷放大器上设置某一灵敏度参数S(一般为出厂给的参考灵敏度),记录压电式力传感器输出力值F,则根据灵敏度定义可知实际真实灵敏度为

(7)

其中S0和mb是未知,可通过2个不同质量块进行测量,获得2组数据,联立求S0和mb。

2 试验结果及分析

由4个不同附加质量块随意组合,设定频率和控制力峰值范围(见表1),进行测试计算所得实际传感器灵敏度S0和传感器端部等效质量mb如表2所示。分析表2可知:

表2 压电式力传感器灵敏度校准结果 (考虑传感器端部等效质量)

(1)考虑传感器端部等效质量引入惯性力后,所得的实际传感器灵敏度波动性不大而且和传感器出厂给定的灵敏度最大相差0.14%。

(2)Kistler的9321型传感器总质量约90 g,所得传感器端部等效质量约占整个传感器质量的64%,不同质量块组合所得的传感器端部等效质量虽稍有差异但与均值相差最大仅为2.45 g。

(3)附加质量块的质量较大或过小都不合适,本项目选择了传感器质量约占附加质量块1.2%～6.6%的质量块,在频率和控制力值相同情况下,不同质量块的随意组合所得传感器端部等效质量具有一致性。

虽然压电式力传感器固有频率很高,但是相比于压电式加速度计,厂商往往提供加速度计传感器的频域特性图,对于压电式力传感器仅提供灵敏度等参数,不提供频域特性图信息。原因就是压电式力传感器的动态特性很大程度上受到安装环境和安装结构的影响,其有效使用频率范围受到安装谐振频率的限制。其频域特性如图6所示。其中f为测量频率,f0为压电式力传感器安装于结构后系统的固有频率。据Kistler的技术资料,当f/f0≤0.1时,传感器精度可以达到1%;当f/f0≤0.2时,传感器精度为5%;当f/f0≤0.3时,传感器精度仅有10%。

图6 压电式力传感器频域特性图

压电式力传感器和附加质量块安装于标准振动台上,测试系统如图7所示,给予系统白噪声激励,采用动态信号分析仪测量系统频响函数进而确定系统固有频率[14]。白噪声激励系统台面功率谱密度如图8所示,进而得到4个不同的附加质量块和传感器分别安装于振动台上后整个系统固有频率如表3所示。

表3 振动系统固有频率 Hz

图7 振动系统频率响应特性测试图

图8 白噪声激励系统台面功率谱密度

以附加质量块A和B为一组,附加质量块C和D为另外一组进行试验,结果如表4所示。结合表3和表4分析可知:

表4 传感器灵敏度随频率变化图(本项目幅值比 以出厂灵敏度S作为比较对象)

(1)即使压电式力传感器的固有频率很高,9321型传感器甚至高达55 kHz,但是其有效的使用频率范围受限于系统安装谐振频率,其适用范围甚至只有几百Hz。

(2) A和B组合计算灵敏度S0时,系统固有频率可以认为f0≈1 500 Hz,分析表4可知当f/f0≤0.1时,满足1%精度等级。C和D组合计算灵敏度S0时,系统固有频率可以认为f0≈1 100 Hz,同样在f/f0≤0.1时,满足1%精度等级。

(3)通过表4可知,由于A和B组合情况相比于C和D组合情况的系统固有频率高,所以在保证精度相等下,A和B组合传感器的使用频率范围较高,甚至在200 Hz时精度等级为2.5%,而C和D组合的灵敏度误差为4.9%。

(4)分析图9可知,C和D组合比A和B组合所得灵敏度在低频阶段波动大,而且A和B组合所得灵敏度更接近于出厂灵敏度,随着频率增加,C和D组合所得灵敏度更加偏离出厂灵敏度。

图9 传感器灵敏度随频率变化图

3 结束语

首先在假设整个质量块为刚体,整个质量块加速度等于表面中心的加速度,并采取不同质量块安装扭矩相等和测量加速度位置的固定等措施,以减少其他未知因素对灵敏度测量造成影响的情况下,设定参考频率,不考虑传感器端部等效质量,研究了灵敏度随附加质量块质量的变化关系。得出质量增加,灵敏度以递减的方式趋向于真实灵敏度,推理并经试验得到当质量块约大于传感器质量的120倍时,可不考虑传感器端部质量对灵敏度标定的影响。进而建立了基于正弦法的压电式力传感器校准的数学模型,通过4个不同质量的质量块随意组合,计算传感器端部等效质量,定量具体研究了传感器端部等效质量引入的惯性力对灵敏度的影响大小,实现了不同质量块计算的灵敏度数值的相互吻合。

最后分析了传感器和附加质量块安装于结构后的系统频响特性,通过试验研究了传感器有效使用频率受系统固有频率的影响并具体研究了传感器精度等级与试验频率和安装谐振频率比值的关系,得出当比值f/f0≤0.1时,压电式传感器具有较高的1%的精度。

力传感器的动态校准及可靠量值溯源性,目前仍然是力学计量校准中动态计量研究的主要内容之一[15],还应重视质量块大小形状以及加速度分布不均匀的研究;由于传感器灵敏度受安装结构系统的固有频率影响很大,因此也很有必要开展现场校准技术和校准的力值范围及有效频率响应范围扩展的研究[16]。