高精度交流电压有效值测量技术研究

杨春玲,王金阳,温星曦,齐 超

(1.哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨 150001;2.北京东方计量测试研究所,北京 100089)

0 引言

随着电子技术水平和制造水平的不断提高,为了满足科学研究以及生产的实际需求,数字万用表的性能不断提高,功能也日益完善[1]。现在工业为保证生产的安全性及研究的准确性,对测量的要求越来越高,因此需要进一步提高数字万用表的测量精度[2]。

目前,国际上的台式数字万用表精度可以达到八位半,并且可以实现多种测量功能和计算功能[3],如美国的Agilent 3458A、Fluke 8508A和日本的Adva ntest R6581,这些产品的精度高,稳定性强。作为万用表重要功能之一的交流电压测量,通常将交流信号转换成直流信号,通过对直流量的测量从而得出交流电压有效值,转换方法有很多,如热电转换法、平均值法、数字采样法、真有效值法等[4]。美国国家标准学会(NIS)电气计量学系提出了一种利用热变换器处理交流电压的方法,通过交流分压器将被测信号调理为1 V交流电压,热电偶由于存在塞贝克效应在电压变化时会产生温升,通过测量温升测量调理后的交流电压[5-7]。Agilent 3458A使用数字采样的方法,采用专用的“多斜积分”式 A/D 转换器,利用电荷平衡原理将参考信号中的电荷用来中和输入信号中的电荷[8],从而保证低速测量的高精度要求。

基于目前国际上数字万用表研究现状,本文针对交流电压测量精度和稳定性进行研究,设计并研究了交流数字采样系统,达到有效值在0.3～3.3 V的范围,频率在45～10 kHz范围内最高不确定度40 ppm的指标(1 ppm=10-6)。

1 高精度交流电压有效值测量方案设计

交流电压有效值是表示交流信号电压指标的参量。本文基于数字采样的方法进行交流电压有效值测量,在现有高精度A/D转换器的基础上,通过改进采样方式,提高有效值计算精度以及抑制测量误差来实现高精度的交流电压有效值测量。交流电压有效值测量方案结构图如图1所示,方案主要分为5个模块,包括信号调理电路、A/D转换器、测频电路、FPGA模块和STM32微控制器模块。

图1 高精度交流电压有效值测量方案

输入待测交流信号首先进入信号调理电路,STM32通过对输入信号不同的幅值来进行信号调理电路中通道选择,对电压有效值较低的输入信号进行放大,对电压有效值较高的输入信号进行衰减,使得交流信号的动态范围变小。经过信号调理电路调理后的交流信号通过测频电路转换成方波信号,此测频电路即为过零检测电路,之后由FPGA进行测频操作,FPGA分别对转换后的方波信号和标准时钟信号进行计数,将2个计数值通过FSMC通信发送给STM32微控制器模块,STM32根据接收的计数值计算输入信号的频率,根据不同的频率值会设定不同的A/D转换器的采样率,并通过FSMC通信将采样率发送给FPGA,再由FPGA向A/D转换器发送采样时序信号。

获得采样时序的A/D转换器对经信号调理电路之后的输入信号进行数字采样,在转换完成后,将采样的数字信号返回给FPGA,再经FPGA将采样的数据发送给STM32,由单片机完成交流电压有效值的计算,并将有效值计算结果发送给PC机。

方案中的信号调理电路与测频电路的硬件电路图如图2所示。

图2 硬件电路图

目前设计信号调理电路的作用分为2部分:衰减和平坦度补偿,衰减采用阻容分压的方式,通过不同的衰减比例选择不同的电阻与电容参数。由于阻容分压可能会存在频率特性平坦度不足的情况,因此选用D/A转换器形成虚拟微调元器件,调整电路的平坦度,这里的DAC为乘法型DA,其参考电压VREF可以用来作为输入,通过改变DA的数字输入量对信号进行有效值调整输出,本文选用的DAC为AD5452。此外,硬件电路还包括测频电路,测频电路的主要作用是对信号调理电路输出的交流电压进行过零检测,将交流电压转换成方波信号提供给FPGA进行测频,本文选用LM393作为比较器。

2 交流数字采样系统工作机理

2.1 交流数字采样技术的数学模型

交流电压的有效值计算公式为

(1)

将式(1)离散化,用1个周期内的有限个采样电压的数字量来代替1个周期内连续变化的电压函数量,如图3所示。

图3 交流电压函数的离散化

则电压的有效值可表示为

(2)

式中:N为交流电压信号1个周期内的采样个数;ΔTm为数字采样的采样时间间隔;um为第m+1个时间间隔内采样的电压瞬时值。

若令采样时间间隔相等,则交流电压有效值计算公式可以改写为

(3)

式(3)是根据1个周期内各采样点的瞬时值与周期采样的个数计算电压有效值的公式。

2.2 顺序等效采样方法的原理分析

数字采样的精度与采样率的大小有直接关联,只有不断提高数据采集的采样率,才可以最大可能提高交流测量精度。顺序等效采样需要根据输入信号的频率设定采样频率,且采样频率还会根据输入信号频率发生改变,即对于重复性周期信号,每个周期采样频率一致,下一个采样周期采样点会在上一采样周期采样点基础上顺延一段时间,从而在连续采样多个点后还原输入信号的波形,即要求采样频率与信号频率同步。顺序等效采样的采样示意图如图4所示。

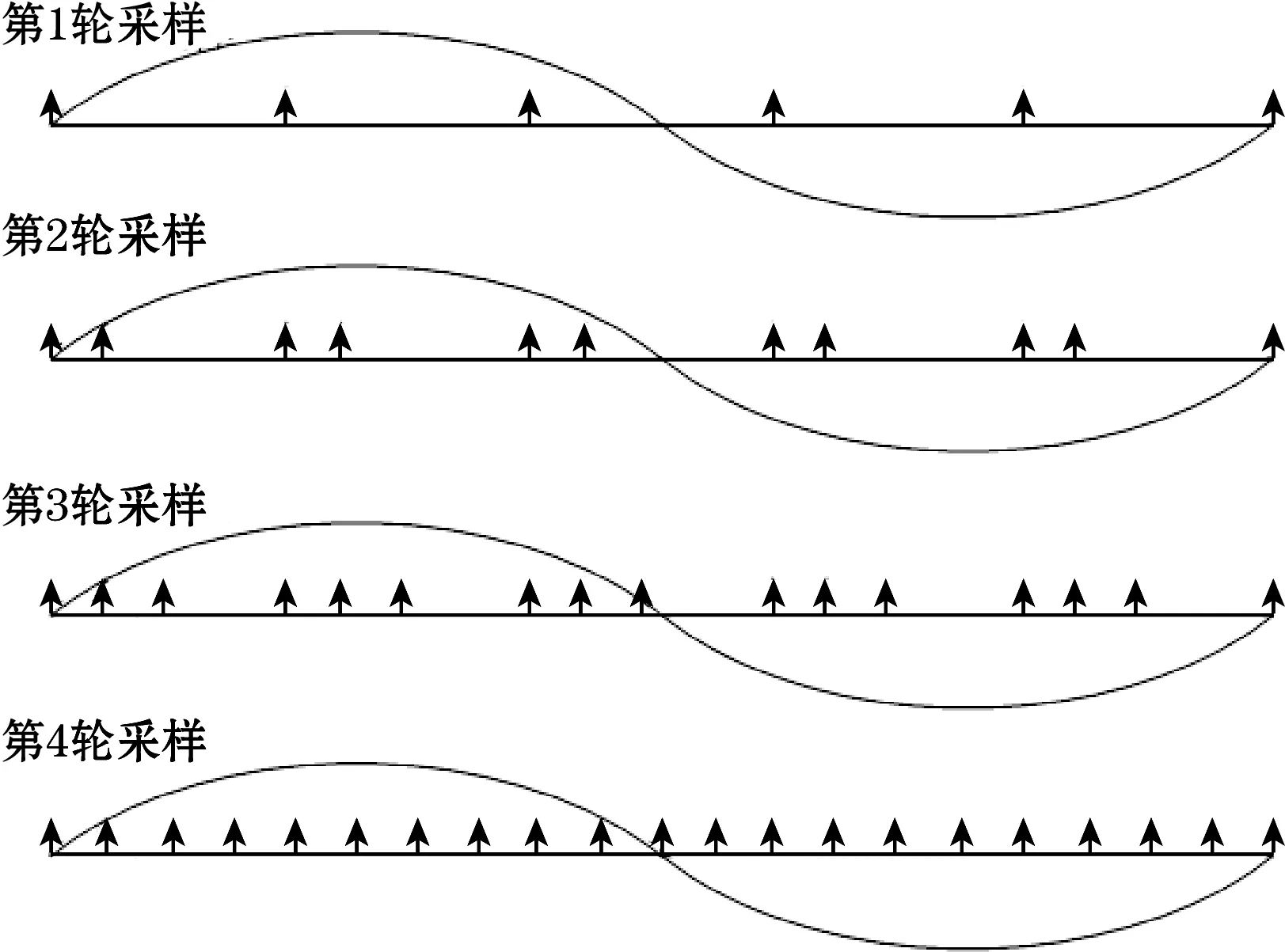
图4 顺序等效采样示意图

假设采样频率是输入信号频率的5倍,1个输入信号周期可以采样5个点,想要利用顺序等效采样的方法在每个信号周期采样20个点。首先,定时电路等待1个正的过零点,然后以最快的采样率进行5次采样,即为第1轮采样。在随后的第2个周期内,时基延迟的时间等于ADC最小采样间隔时间的1/4,并且再次读取5个读数,这显示为第2轮采样。此过程一直持续到第4遍,此时输入波形应为等周期,从而使ADC获取数据的速度等效为实际速度的4倍。

3 交流数字采样系统误差分析与抑制

3.1 系统误差分析

交流电压有效值测量技术通常采用不确定度来衡量。不确定度的含义是指由于测量误差的存在,对被测量值的不能肯定的程度,是测量结果质量的指标。不确定度又分为A类不确定度和B类不确定度。

A类不确定度评定的依据是频率分布,采用统计分析的方法评定,通常用试验标准差表示。B类不确定度的依据是先验分布,信息的来源一般是对于仪器特性的了解,此时不确定度定义为具有90%、95%、99%包含概率的一个区间。一般情况下,对于交流电压有效值测量技术不确定的评定,选取A类与B类合成评定的方法。

测量误差分为系统误差与随机误差2部分,随机误差是指测量结果减相同条件对同一变量无限多次测量结果的平均值,而系统误差为重复性条件下对被测量的无限多次测量结果的算术平均值减被测量真值。对于本文而言,整个系统内每一部分误差的大小和方向未能明确掌握,而我们需要估计出其不致超过某一极限范围的系统误差。对于未定系统,将其误差按照标准差合成,有以下公式:

(4)

式中:ui为s个未定系统的误差;σi为q个随机误差。

由于随机误差是以算术平均值为中心呈对称正态分布,而系统误差来源于影响量,只能通过校准修正来减小其影响。通过多次测量,可以将随机误差显著减小,因此系统最后不确定度是由系统误差产生的,而系统误差可以通过修正的方法解决,因此只需研究未定系统误差的分配问题。如果每个模块dxi的误差分量之间互不相关,则系统的总误差为

(5)

根据主要项分配原则与等作用分配原则,可以认为各部分对函数误差的影响相等,可以推出:

(6)

本文由信号调理电路、A/D转换器以及采样时基触发网络和数字采样算法4部分产生系统误差,因此,n=4,取置信度为99%时的包含因子k=3,并根据指标要求不确定度最好为0.03%,可以计算得到此时每一部分系统误差为

(7)

3.2 数字采样积分算法

3.2.1 积分算法误差分析

一般情况,数值积分的方法有Newton-Cotes公式、梯形公式、辛普森公式、拉格朗日插值等算法,一般情况下,对于普通正弦信号,采用梯形方法求数值积分,公式如下:

(8)

其中f(x)为区间(x0,x1)内的二阶可微分函数,根据求数值积分梯形公式的误差及积分中值定理可以求得误差,存在η∈[x0,x1],使得:

(9)

根据误差公式对式(3)进行误差估计,设输入信号为f(x)=[Asin(x)]2,可以求得U2的误差α为

(10)

电压有效值在整周期内的绝对误差为

(11)

3.2.2 基于顺序等效采样的积分算法误差抑制策略

考虑系统对积分算法误差的要求,根据式(10)可以得出数字采样系统在每个周期的采样数据需大于363,考虑到FPGA的时钟以及不同频率量程对于误差大小的要求不一致,本文采用100 M的等效采样率,这样对于高达200 kHz的输入交流信号可以满足积分误差允许范围。

结合之前顺序等效采样的原理分析,根据输入信号的频率设定采样频率,每隔1个或几个信号周期,采样点顺延一段时间,从而在连续采样多个点后还原出输入信号的波形,本文对于这种抑制策略进行仿真分析,对于100 kHz输入交流信号,每个周期采样1 000个点合成正弦波,最后计算得到的有效值相对误差为2.897 5 ppm,满足指标要求。

3.3 数字采样时基抖动

3.3.1 采样时基抖动误差分析

数字采样过程中,采样时刻的准确性会对整个采集系统的精度产生影响。假设等效采样是从基准点以ΔT为时间单位进行延时采样的,假设实际采样点与理想采样点之间的误差为±Δt,则采样点时刻为nΔT±Δt,±Δt是期望为0的平稳随机变量,在对采样的数据进行波形重建时,会将nΔT±Δt点的采样数据作为nΔT时刻的采样点加以还原,这就在等效采样过程中引入了孔径误差。图5为孔径误差对采样数据的影响。

图5 孔径误差对采样数据的影响

当A/D转换器满量程输入电压为VFS,输入交流信号频率最高为f时,孔径时间Th内最大幅度变化值为

ΔV=VFSsin(VFSTh2πf)

(12)

实际抖动误差可以计算为

(13)

3.3.2 基于过零检测的采样时基抖动误差抑制策略

在等效采样过程中,需要准确知道过零点的时刻,这样才能准确确定采样点时刻,以完成高精度的等效采样,但是由于FPGA时钟的限制,并不能准确得知过零点时刻,误差示意如图6所示。

图6 过零检测误差示意图

由图6可以看出,过零检测电路会使实际过零点与检测过零点有一定误差,这与检测时钟频率有一定关系,本文选用100 MHz的时钟,这也导致实际过零点与检测过零点之间最大误差可以达到10 ns。根据之前所述等效采样的方法会导致在过后的采样点中都会存在这样误差,导致采样时刻不确定。式(14)是1个采样时基抖动产生的相对误差。

(14)

式中n为时基抖动误差的个数。

按照上述分析,N最小值为363,则可得到n的最大值为182,本文选取n为100。

第1种采样方式如图7所示。已知输入信号周期之后,找一个合适的采样周期,这个采样周期只比信号周期的倍数多10 ns,这样多个采样周期采集到的信号就会每次错开10 ns相位。例如,信号是1 MHz频率的,周期1 μs,假设ADC最小采样周期是1 μs,取1 μs+10 ns作为采样周期,这样每次采样后把这些采样点拼出来,就是等效100 MHz采样的信号样都相当于在第一次采样的基础上错开10 ns的相位得到的采样。

图7 第一种等效采样示意图

这种采样方法对于ADC的直接采样率有较低的要求,但是会导致每个采样点都引入时基抖动误差,即每个等效采样周期如果有1 000个采样点,便会引入1 000次时基抖动误差,这不符合采样时基抖动误差抑制策略。

第2种采样方式如图8所示,根据过零检测电路与消抖电路可以得到输入正弦信号对应的方波信号,对此方波信号进行二分频后,在二分频信号的高电平时段进行数据采样,每个采样周期的初次采样信号选定在过零点后的10 ns、20 ns、30 ns…,并且在每个采样周期内都按照1 MSPS的采样率进行直接采样,按照这样的采样方法,完成100个采样周期便可实现100 M/sps的等效采样频率。

图8 第2种等效采样示意图

从分析可以看出,每个周期的采样只有第一个采样点存在采样时基抖动,之后的采样点都是在该采样点基础上准确延时1 μs,不会额外引出时基抖动误差。因此对于最高100 M的等效采样率,也只需要100个周期的采样数据结合,这样只引入了100次采样时基抖动误差,符合设定的n=100的指标要求。

对于数字采样时基抖动误差的抑制策略进行了仿真分析,对于10 kHz输入交流信号,按照100 MHz的等效采样率分别按照2种等效采样方式进行仿真,分析加入与不加时基抖动误差对于两种采样方式的有效值计算是否有影响,其中误差结果如图9所示。

(a)第1种采样方式未加抖动误差

图9(a)、图9(b)表示不考虑抖动误差与A/D转换器误差情况下,2种采样方式的有效值计算误差,图9(c)、图9(d)表示考虑抖动误差(不考虑A/D转换器误差)时2种采样方式的有效值计算误差。可以看出第2种采样方式显著减小了采样时基抖动造成的有效值测量误差,误差可以减小至10-15量级,而对于第一种采样方式,仅可以达到200 ppm量级,因此可以得到第二种等效采样方式是有效的时基抖动误差抑制策略。

4 自动测试系统与实验测试结果

4.1 自动测试系统的搭建

构建的自动测试系统如图10所示,包括上位机、研制的交流电压有效值测量系统以及交流电压标准源/校准器。

图10 自动测试系统

使用LabWindows/CVI编写上位机程序,上位机可以给交流电压标准源/校准器发送设置指令,从而输出交流电压信号,同时,上位机通过串口通讯将指令发送给交流电压有效值测量系统,系统中单片机对该指令进行解析,将解析后的命令发送给FPGA,FPGA向A/D转换器发送采样时序,采样数据由FPGA发送至单片机,再由单片机通过串口通讯返回到上位机,上位机可以对串口返回的数据进行参数设置,设置返回数值个数与返回数值时间间隔,将返回的交流有效值存入Excel表格中。

4.2 交流数字采样系统实验测试结果

选用FLUKE5500A作为自动测试系统的交流电压校准器,其90 d最低不确定度在0.33～3.299 99 V的量程、频率在45～10 kHz下可以达到0.02%±60 μV。实验室环境温度变化在2 ℃以内,在交流电压校准器和数字采样系统预热0.5 h后开始采样,采样间隔为3 s,每次测试共采集800个点,重复多次测试。

设定输入信号频率为10 kHz,有效值为1 V,测试结果如图11所示。

图11 输入信号10 kHz,1 V下系统测试结果

由图11可以看出,测试结果的电压值的极差在40 μV左右,按照99%的置信区间对不确定度进行计算,取包含因子k=3,有如下公式:

(15)

计算得到的测量不确定度为27 ppm。表1给出了在输入信号频率保持10 kHz,改变不同的输入有效值所得的测试结果。

表1 交流数字采样系统10 kHz测试结果

调节输入信号频率为20 kHz,有效值为3 V,测试结果如图12所示。

图12 输入信号20 kHz、3 V下系统测试结果

由图12可以看出,测试结果的电压值的极差在250 μV左右,计算得到的测量不确定度为34 ppm。表2给出了在输入信号有效值保持3 V,改变不同的输入信号频率所得的测试结果。

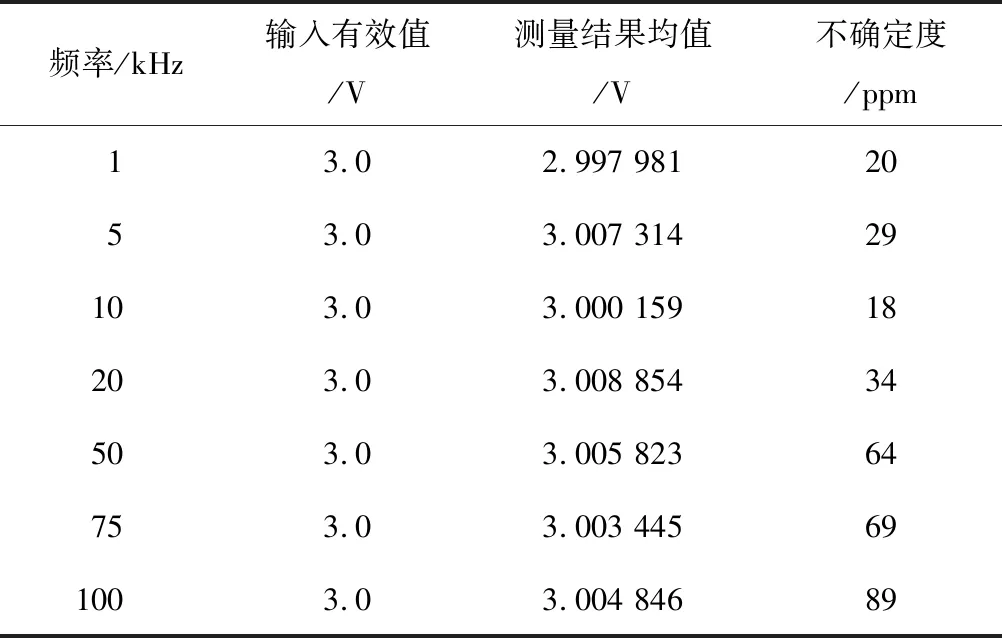
表2 交流数字采样系统3 V测试结果

5 结论

本文基于数字采样方式研究了交流电压有效值测量技术。针对有效值测量的高精度要求,对系统进行误差分析,探究误差来源,提出抑制策略。对于有效值计算中的积分算法误差,通过改变数字采样方式,以顺序等效采样为核心进行误差抑制;对于采样时基抖动引起的误差,引入过零检测与消抖电路,提高了测量的准确性。进行软件设计,搭建自动测试系统,实现直观简便的人机互动和与测量系统的数据传输。对交流数字采样系统进行总体测试验证,通过测量结果可以看出,系统在有效值测量范围为0.3～3.3 V,频率测量范围在45 Hz～10 kHz,最高不确定度在40 ppm以内,系统工作稳定可靠,符合设计指标,可以满足高精度交流电压有效值测量的需求。