粒度信息决策算法之差转计算应用研究

赵 静， 包研科

（1 黔南民族师范学院数学与统计学院， 贵州都匀 558000； 2 辽宁工程技术大学理学院， 辽宁阜新 123000）

0 引 言

因素空间理论是汪培庄先生于1982 年提出，旨在描述随机性和模糊性本质规律的数学理论，与认知科学交互，成为数据科学与智能科学的基础理论和概念与知识表达的普适性框架［1］。 2014 年，汪培庄发起并主导了因素空间在数据科学中的应用问题的讨论。 同年，包研科［2－3］在因素分析法的基础上，结合因素空间理论，提出名为“差转计算（The set subtraction and rotation calculation，S＆R）”的多因素决策算法，并深入讨论了其决策过程的深层理论背景和几何结构。

差转计算以有监督类数据为操作对象，挖掘其内部蕴含的规律，表现为“if…，then….”结构的规则模型，其决策机制是建立在人脑解决分类问题的认知原理之上，在定性因素的多因素分类问题中取得了较好的实测效果［2］。 2017 年，包研科［4］给出定量因素上的差转计算修正算法，拓展了差转计算的应用场景。 自差转计算提出以来，笔者所在团队进行了大量的算法测试与验证工作。 文献［4－5］以及非公开的算法测试结果表明，差转计算算法在定性变量的样本数据集上，在规则挖掘效率和泛化性能上优于定量变量的样本数据集。

因素空间理论认为决策问题是问题研究所在论域内概念的认知过程［5］。 决策过程实质是论域内研究对象的分类识别问题，从人工认知学角度来讲，决策问题应当在条件信息数据与决策信息数据支撑下回到论域中进行讨论样本的归属。 基于此，差转计算的决策机制是构建条件信息数据与决策信息数据到论域的凸包，并基于凸包内样本数据建立决策准则，诱导出“if…，then…” 语句的推理知识，同决策树类似。 差转计算的基本决策过程是基于统计信息构建数据空间到认知本体的划分类，对于差转计算的某一次决策过程，划分形成等价类有3 类关系如图1 所示。

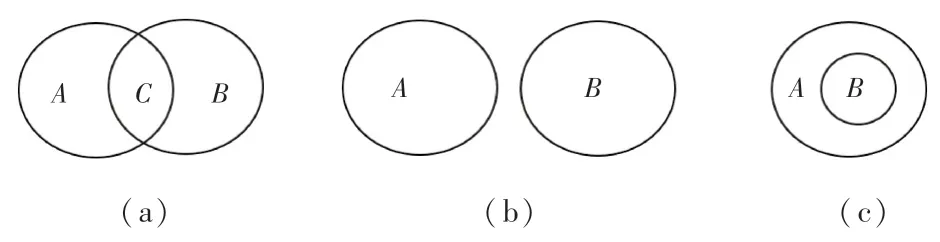
图1 等价类的3 种关系Fig. 1 Three relationships of equivalence classes

图1 中A、B、C 表示差转计算依条件信息数据与决策信息数据对论域形成的划分类。 图1（b）、（c）两类关系可归结为线性可分和完全包含关系的分类识别问题，现有算法如感知机、支持向量机等能够很好解决此类问题。 关键问题在于如何有效识别图1（a）中C区域中对象的归属。

不同分类算法在处理区域C时采用的方法不同，应用较为广泛的方式是基于样本数据采用降维技术将数据变换到区域A或B中，存在的风险是数据失真，进而可能导致分类结果不准确的情况。 在保证数据不失真的情况下，还能有效识别区域C内对象归属问题，可以考虑采用升维的方法，从因素空间理论的角度来讲，需要引入新的指标，即隐性条件因素的发现，文献［5］在这个方面做了突破性工作，但尚未进行深入研究。

本文基于因素空间和商集合理论背景下，提出一种基于信息粒度变换的数据处理方法，本质是变换数据观测视角，在不同视角下对论域进行划分，形成有效决策知识。 为验证本文所提方法的有效性，将该方法结合差转计算，并应用于样本数据为离散型的多因素分类决策问题中。

1 基本概念及差转计算算法原理

分类问题是人脑认知过程的主体，分类算法的设计过程应符合人工认知的4 个基本原理［5］。 为方便理解本文工作，就差转计算所涉及概念进行阐述。

1.1 因素及其运算

科学研究是在特定研究范围内对存在的问题进行证伪的过程，根本目的在于形成符合人类认知结构的知识，而知识由概念表达，概念的阐述由内涵和外延对合构成。 差转计算的根本目的是基于统计信息挖掘内在规律性知识。

定义1称问题研究过程中讨论的所有对象ui构成的可列集合U为论域，记为式（1）：

统计研究过程中，论域U内研究对象是有限的，即式（2）

定义2称满映射，即f：U→If为定义在U上的因素，即对∀ui∈U，在If存在一个性态特征d，使得f(ui)＝d，If是论域U中对象ui在f上表达出的性态特征构成的集合，称为f的相态空间。

实际应用过程中，性态d存在空置的风险，即统计样本存在缺失值。 因素空间理论认为缺失值亦是特殊相态值。

因素按照其发挥的功能可分为条件因素和结果因素。 本文中若无特殊指代，一般因素指的是条件因素。 以有监督数据为例，类别或标签数据对应指标即为结果因素，提供决策信息；除结果因素以外的指标称为条件因素，提供决策条件参考信息。 按照相态空间数据属性可分为连续型因素和离散型因素。

定义3设映射满足：称为因素f的回溯（Recall）。

回溯是因素的广义逆映射。 回溯概念的定义为条件信息数据与决策信息数据回到论域中进行构建划分提供了方法和工具。 因此，由因素及回溯定义，不论是条件因素，还是结果因素，均具有两个功能：

（1）因素是概念的本位属性限定工具，即式（3）和式（4）：

其中，[d]f是对象ui由因素f的回溯在论域U中构成的等价类，是概念外延在数据科学中的表达。

上述定义不仅建立了基于因素空间理论的数据挖掘算法独特的数学基础框架，亦可保证基于数据的概念表达内涵描述与外延描述的一致性。

1.2 算法原理及步骤

差转计算的算法本质就是将决策信息和条件参考信息构成的本体关系映射到条件因素上。

定义4设论域U中样本容量为n，称对各个样本ui的顺序编号构成的集合为U的秩序集。 若A是U／f中任意的含有s个对象的等价类， 记为A的秩序子集， 则称为A的f—表征，记为Rf(A) 。

定义5设f和g是同时定义在论域U上的因素，对称为等价类[l]g在f上的踪影（Representation）。定义6称为因f的相态排序而形成的第k个聚集子块（简称子块），满足式（7）和式（8）：

定义7设f和g是同时定义在论域U上的因素，其相态空间分别记为If、Ig，且If存在序关系，若∃t∈If，∃l∈Ig，满足式（9）：

则称式（10）

为因素f对g的预测系数或决定度，并称［t］f是［l］g的f决定类，其中pro(★ ) 表示对★求统计频率。 若则称f∗为优势因素。

为清楚阐述定义4 ～定义7 描述概念及其转换关系，假定对因素f的相态排序后形成如图2 所示的概念转换示意图。

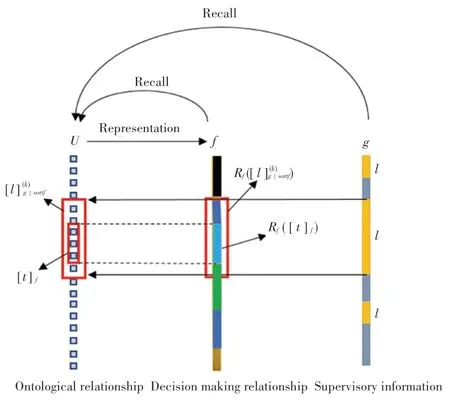
图2 概念转换示意图Fig. 2 Concept conversion schematic

图2 中，表示等价类[l]g由于因素f的相态空间排序而形成的第k个子块。 决策问题是关于论域中对象归属问题的讨论，因素g表征了决策信息，只能提供决策参考，从因素回归到论域中进行讨论是因素空间的基本思想。 因此，决策的本体关系是但决策的观察是发生在因素f上的， 算法的表述是差转计算算法原理如下：

差转计算的算法原理［2］假定f和g是论域U上的离散型因素，由f和g定义的两个概念记为

εf(ui，k)＝（k，[k]f） 和εg(ui，r)＝（r，[r]g），则复合推理句∀ui∈U，若f(ui)＝k，则g(ui)＝r，恒真的充分必要条件是[k]f⊂[r]g。

基于前述定义及原理，差转计算实现了由样本数据空间到研究论域的分类决策过程，差转计算在分类决策过程中的算法步骤：

算法差转计算

输入有限样本数据集S见表1。

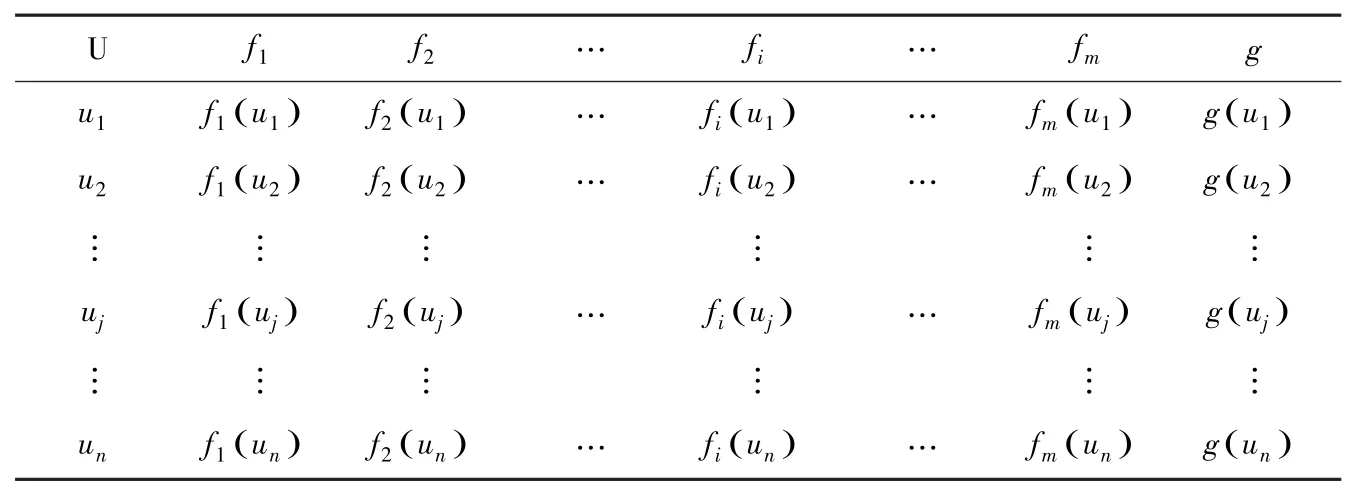
表1 有限样本数据集STab. 1 Limited sample data sets

初始化：复合推理知识集合R＝Ø；样本集内样本个数；

过程：差转计算算法

（1）判断是否大于0。 是，计算每个因素fi，i＝1，2，…，m的决定度；否，算法结束；

（2）定位优势因素f∗， 记其决定度为δf∗， 转（3）；

（3）判断δf∗是否大于0。 否，则转（5），算法结束；是，依据辨识决定类，则转（4）；

（4）形成推理语句R′： 若f∗(ui)＝t， 则g＝l，将R′加入到R中，在S中删除［t］f∗对应数据，更新S，则转（1）。

输出复合推理知识集合R，算法结束。

由上述过程可以看出，差转计算算法结束的要求有：

（1）删空操作数据集；

（2）在数据集非空情形下不能形成有效决定类，此类情形极容易造成决策信息丢失，进而影响算法泛化效果，本文核心工作在于利用粒度信息变换去解决此类情形下的决策问题。

另外，因素空间中因素分析法与差转计算法在规则知识发现的过程中区别是第（4）步骤的不同，因素分析法既要删除因素分析表中对应因素，又要删除因素分析表中决定类对应数据，而差转计算仅删除决定类对应数据。 从认知学角度来讲，差转计算更符合人脑辨识事物的过程。

2 粒度变换的思想和原理

分类决策研究最核心的问题在于辨识图1 中区域C内的对象的归属，存在不能描述不同类型的因素在概念形成过程中的作用的局限［5］。

因素空间中对于区域C的对象归属一般采用不同视角进行辨识，即利用不同因素构建等价类包含关系，但亦避免不了上述局限性。 数据科学中，大多算法对区域C的辨识，在实际应用中一般采用指标间相关性进行降维，将数据变换到区域A或B中，从而实现有效分类，但存在数据失真的问题，导致最终分类结果不准确的风险；值得一提的是决策树算法在此类问题中表现出较好的特性，其决策过程依赖指标同样本之间的统计数据构造指标分类节点，但亦存在依靠“贪心策略”得出的分类节点不可回溯，某些树枝对应的规则的支持度相对较小，从而规则的可靠性也较小，很有可能使推理出来的规则存在系统误差的问题［4］；另外一种依赖统计数据构造推理知识的算法是关联规则，其基本过程是采用水平组织逐层搜索的迭代方法形成推理知识，但其过度依赖数据样本的背景空间，推理出的知识亦仅局限于数值关系表达，不符合人脑辨识事务的基本过程［6］。

为此，本文构造基于统计数据中因素升维观测的粒度变换方法，进而结合差转计算实现多因素知识挖掘过程。

2.1 粒度变换原理

因素空间中维度变换由因素的析取与合取运算实现。

定义8（因素的析取） 设f和g均为定义在论域U上的因素，称运算h＝f∧g＝g∧f为因素f和g的析取运算。

因素的析运算旨在描述因素f和g在概念形成过程中的协同作用，进一步可理解为概念的分化功能，即析取因素越多，划分的概念越明确。

其概念外延划分功能由下述定理实现：

定理1［5］（析运算基本定理）U／f∧g⇔U／f°U／g，其中U／f°U／g为商集U／f与U／g的积。

定义9（因素的合取） 设f和g均为定义在论域U上的因素，称运算c＝f∨g＝g∨f为因素f和g的合取运算。

因素的合取描述了因素f和g在概念形成过程中的协同作用，进一步可理解为概念的同化功能，即因素析运算中因素越多，划分的概念越“粗糙”。

概念外延划分功能由合运算基本定理实现。

定理2［5］（合运算基本定理）U／f∨g⇔U／f＋U／g，其中U／f＋U／g为商集U／f与U／g的和。

上述定义及定理既实现了因素空间到数据空间的联立，又实现了概念内涵和外延之间的对合关系，图1 中区域C内对象的辨识问题实质是分化概念对其外延的对合描述问题，是分化和同化的暂时平衡。

定义8、定义9 和定理1、定理2 为新因素的引入及其相态空间的构造提供了方法，新因素的引入旨在变换观测角度，或提升观测维度。

2.2 粒度变换步骤

差转计算在知识挖掘过程中以决定度为决策准则，依据人工认知基本原理，决定度过低不利于推理知识的形成，决定度过高则影响泛化性能；决定度过低，其样本反变到图1 中区域C内，无法进行有效辨识，此时，由定义8 可联立因素进行升维观测，旨在发现能够辨识样本的知识，升维的过程既涉及新因素的引入，又涉及新因素相态空间的构造，实质是利用原始样本数据重构数据空间。

为描述简单，假设数据升维观察仅涉及两两因素联立，多因素联立过程以以下步骤外推得到。 设D是论域U上原始有限样本数据集，∀fi，fj，i≠j为定义在D上的离散型条件因素，其相态空间分别为Ifi，Ifj，g为定义在D上的结果因素。 不失一般性，记Ig＝ {1，2，…，s} ，重构样本数据空间过程中结果因素及其相态空间保持不变。 重构步骤如下：

输入有限样本数据集D

过程：数据升维算法

步骤1对因素分别求因素fi，fj在D内的等价类，即分别代表Ifi，Ifj中相态种类数；

步骤2求集族C＝｛Cp，q ｜Cp，q＝Ap∩Bq，Ap∈A，Bq∈B，p＝1，2，…，n，q＝1，2，…，l，Ap∩Bq≠φ｝；

步骤3求不相交并集族π(C) ， 即若∃Cz，Cr∈C，Cz≠Cr，Cz∩Cr≠ϕ，在C中删除Cz，Cr并将Cz∪Cr加入到π(C) 中；

步骤4记联立因素为hi，j，此步骤为构造相态空间Ihi，j。 由步骤3，记则即有

为方便理解重构过程，以实例结合进行阐述。

记待挖掘数据集D见表2。

表2 待挖掘数据集DTab. 2 The dataset D to be mined

显然，差转计算决策准则此时不适用，无法进行有效知识挖掘，需进行数据升维观测，旨在联立因素扩大解析能力，形成有效决定类。

输入有限样本数据集D，即表2

步骤1因素f1在论域中形成的等价类为；因素f2在论域中形成的等价类为

步骤2求集族， 记

则有：

步骤3求不相交并集族π(C) ， 判断C内元素是否存在交集，依秩序求交并放入π(C) 内，显然C内元素不存在交集，则

步骤4重构相态空间，记h1，2＝f1∧f2，则Ih1，2为 {1，2，3，4，5，6}。

输出变换数据集D′，见表3。

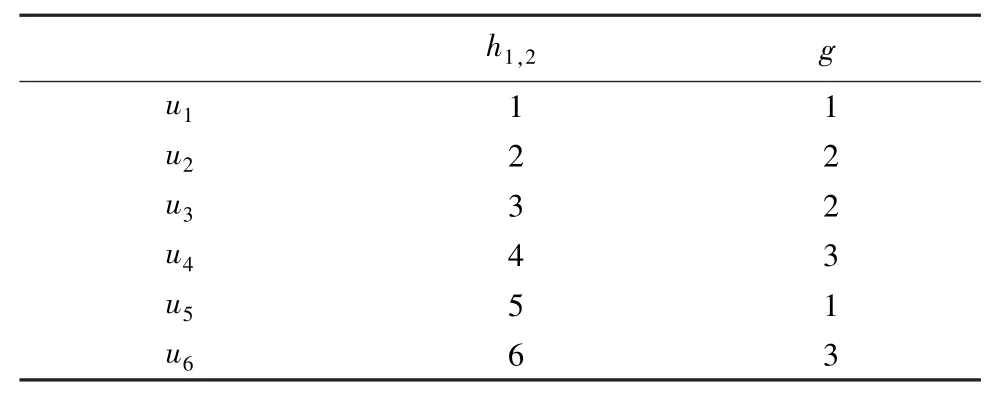
表3 变换数据集D′Tab. 3 Transformed dataset D′

显然，在数据集D′ 上可以进行差转计算，并且形成一一对应的知识类。

值得注意的是在较多因素下的因素升维变换观测很有可能存在组合爆炸的问题，特别是二因素组合带来的数据爆发式增长，极易带来模型应用复杂度的提升。 针对这个问题，本文做出如下构想：可以基于因素轮廓构造决定灵敏综合信息度量，在此基础上可以衍生到在人工认知角度下的多因素适度组合问题，能够很大程度上解决这一问题。

3 实证分析

为验证方法的有效性，将本文所提方法结合差转计算，同时以在知识挖掘过程同为推理算法的决策树作为对比算法，并以UCI 共享数据库中较为经典的Wisconsin Breast Cancer（简记为WBC）为研究对象，采用留出法按比例9：1 将WBC 数据集划分为训练集和测试集，分别利用两种算法对训练集进行知识挖掘，将挖掘出的知识应用于测试集，采用错误率、查准率、查全率、敏感度和F1 综合度量5 个指标对最终结果进行比较。

本文的知识挖掘及模型泛化过程代码均基于MATLAB 2016b 根据差转计算算法原理设计实现，对比算法决策树C5.0 的知识挖掘和泛化过程在商用软件see5 上完成。

3.1 数据说明

数据集WBC 共计699 个样本，包含9 类条件因素和两类结果因素，条件因素名称、类型及值态分布见表4。

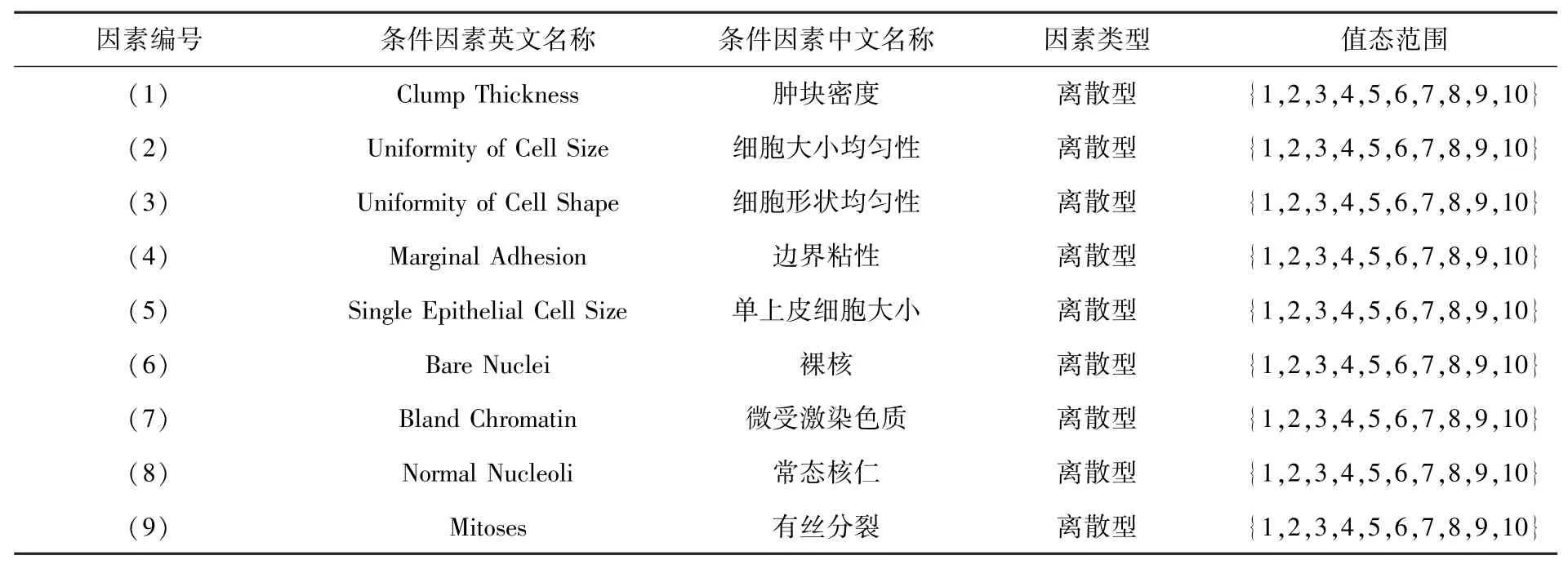
表4 数据集WBC 条件因素名称及值态分布Tab. 4 WBC’s conditional factor name and value distribution

数据集WBC 有1 个结果因素，包含2 个相态良性（benign）和恶性（malignant），各有458 和241 个样例；共有9 个条件因素，每个因素均有10 个相态，相态值按细胞学特征从1－10 分为10 个等级，值态1 最接近结果因素的相态benign，值态10 最接近结果因素的相态malignant。

699 个样本以留出法按9：1 划分为训练集和测试集，在良性（benign）和恶性（malignant）两类别上的样本数据分布见表5。

表5 样本数据分布Tab. 5 Sample data distribution

3.2 测试结果

测试分为两个阶段，分别为知识挖掘阶段和知识泛化阶段。 差转计算在训练集上知识挖掘经历两个过程，分别是单因素决策知识的提取和双因素析取运算下决策知识的挖掘，挖掘出的推理语句序列见表6。

表6 规则知识挖掘结果表Tab. 6 The result of rule－knowledge mining

差转计算在训练集上共计操作12 次，前9 次为单因素规则知识挖掘，第9 次知识挖掘后训练集非空，剩余426 组样本数据；此时单因素不能形成有效决定类，需引入双因素进行信息粒度变换，变换后样本维度为426×37，变换数据挖掘形成第10～12 组双因素规则知识，这个过程仅3 次便使差转计算收敛，收敛速度很快。 整个知识挖掘过程共计执行0.323 s，知识挖掘速度小于在see5 上决策树知识挖掘时间（0.532 s）。

表6 中知识的依次可解读为：若因素（2）取值为5 或10 时，则结果为（malignant）；若因素（2）取值不为5 或10 时，但因素（1）取值为9 或10 时，则结果为（malignant）。

从机器学习角度来讲，知识的泛化一般需要在训练集和测试集上分别进行。 对于知识在训练集上的泛化，不论是从差转计算算法原理，亦或是笔者所作的大量实验来看，差转计算均能在训练集上实现高效决策，准确率几乎达到100%，表明差转计算的学习过程不会产生冗余规则；但决策树并不能达到这一目标。

另外，差转计算及决策树经验推理系统在测试集上的泛化结果见表7 和表8。

表7 差转计算经验推理系统泛化结果Tab. 7 Generalization results of empirical reasoning systems for set subtraction and rotation calculation

表8 决策树经验推理系统泛化结果Tab. 8 Generalization results of empirical reasoning systems for decision tree

若着重关注结果malignant，则两种算法的5 个评估指标结果见表9。

表9 算法评估指标结果Tab. 9 Algorithm evaluation results

可以看出差转计算学习能力是较好的，其经验推理系统的泛化能力也与决策树相当，但整体知识的泛化速度要更快。

4 结束语

差转计算算法本质是根据单一条件信息与决策信息在论域中形成的等价类包含关系诱导出概念知识，但存在不能描述不同类型的因素在概念形成过程中的作用的局限。 为解决这一问题，本文在因素空间及商集合理论的基础上定义因素析取、合取概念，借此实现数据的粒度变换。 实证结论表明本文提出方法是有效的，能够描述不同类型的因素在概念形成过程中的作用，亦能促使差转计算快速收敛，同时挖掘出的知识在泛化过程中决策速率快、决策能力与决策树等同。 另外，本文工作仅作为一个研究基础，所涉及的概念转移、因素组合爆炸问题以及知识的修正过程还有待深入研究。