考虑紧迫度的应急物资轴辐供需网络优化研究

仲舒琳， 倪 静

（上海理工大学管理学院， 上海 200093）

0 引 言

近年来，世界各地突发性公共卫生事件频发，给人类带来了难以估量的灾难，如SARS、甲型HIN1、非洲猪瘟以及COVID－19［1］。 由于该类事件通常具有突发性，受灾地的应急物资在爆发初期往往是不够的，需要从外部进行应急物资调度，高效的应急物资调度网络设计在事件中发挥着重要的作用。

应急物资调度问题是近年来的研究热点之一，Ding［2］构建了基于灰色区间的多个需求点到多个供应点间的应急物资调度，采用NSGA－II 算法，有效减少了包括应急响应系统的时间成本损失在内的总成本；张琳［3］在考虑不确定条件下，构建调度时间最短和调度成本最低的两目标应急物资调度模型，通过LINGO 对其求解，结果表明该模型可以有效合理的进行应急物资调度；王付宇［4］考虑灾害初期道路通行和运输能力的限制，构建灾区平均等待时间最短和物资调度成本最小的双目标优化模型，并通过改进的NSGA－II 算法验证了模型的有效性。

上述研究主要聚焦在物资调度的时效性和经济性，没有考虑到需求点间存在的差异性。 胡晓伟［5］以需求满足率最大为主要目标，兼顾车辆行驶距离，构建应急医疗物资动态分配模型，并通过算例验证了模型的有效性和可行性；单子丹［6］考虑物资需求的紧迫性，构建集散－中心－需求点三级调度网络，有效的缓解资源短缺情况、提高医用物资利用率；赵建有［7］引入受灾点紧迫度量化及分级，构建多目标车辆路径优化模型，满足应急物资配送的时效性、经济性与公平性；刘艳秋［8］在考虑物资分配公平性的情况下，同时考虑道路受损情况，构建应急物流路径优化的两阶段模型，并通过一种混合人工鱼群算法求解证明了模型的可行性。

在供需网络中有些研究考虑三级供应链，供应点－中心－需求点，却忽略了中心之间的物资运输功能，轴辐式网络通过中心轴点间进行连接，形成规模运输，因此轴辐网络通过在轴点间进行资源整合，从而有效提高资源调度效率。 Zhou［9］考虑客户差异化服务需求，构建了多式联运的轴辐式网络模型，获得了总成本最小的最优枢纽位置和分配方案；黄星［10］在模糊筹集时间下构建出具有直达结构和Hub 结构的混合协同筹集的轴辐式应急物资筹集网络，有效的运用于震灾应急物资筹集决策中；Li［11］在COVID－19 背景下基于轴辐式网络考虑多类型紧急救援，建立了以运输时间消耗和运输成本最小化为目标的双目标优化模型，有效的兼顾了时间和成本。

目前，国内外对于应急物资调度的研究已有一定的基础，对公平性的实现主要集中在对物资数量公平性研究上，较少考虑物资分配和时间调度的双重公平。 因此，在突发公共卫生事件下，本文考虑需求点紧迫度，兼顾时间公平和分配公平，构建应急物资供需网络模型。 另外，在应急物资调度网络中，为了提高物资调度效率，采用轴辐式网络可以通过轴点间的铁路进行快速运输，并通过多式联运灵活高效地进行物资调度，因此本文构建考虑紧迫度的应急物资轴辐供需网络模型。

1 问题描述

本文主要研究应急物资调度网络问题，并以最小化物资缺口，最小化时间延误，最小化系统总成本为目标构建网络。 在物资调度过程中，由于突发公共卫生事件初期供应有限，无法满足所有需求点的物资需求，通过衡量需求点间存在差异性评价需求点紧迫度，将物资进行合理分配以满足物资分配的公平。 在此基础上依据轴辐式网络结构特点构建应急物资供需网络，该应急物资轴辐供需网络中有3类节点：供应点、中转枢纽、需求点，轴辐式网络拓扑结构如图1 所示。 供应点和需求点作为轴辐网络中的辐点，中转枢纽作为网络中的轴点，轴点与辐点之间通过灵活性高的公路运输，轴点间则采用速度更快经济性更高的铁路运输，并且允许辐点直接运输，构建多式联运的混合轴辐应急物资供需网络，旨在快速高效地对需求点进行大规模的物资输送。

图1 轴辐式网络拓扑结构Fig. 1 Hub－and－spoke network topology

2 物资调度模型

基于问题及分析，本文构建的考虑紧迫度的应急物资轴辐供需网络模型。

2.1 模型构建

假设突发公共卫生事件发生时， 供应点i（i∈I） 为需求点j（j∈J） 提供物资供应，运输方式为通过枢纽点k、m（k，m∈K） 中转运输或者直达运输。

首先，在考虑需求紧迫度的情况下构建公平性函数F1，式（1）：

其中，λj为需求点j的需求紧迫度；qj为需求点j需求的物资量；qij为供应点i向需求点j实际分配的物资量。

其次，在考虑需求紧迫度的情况下构建时效性函数F2，式（2）：

其中，Tijkm为供应点i经过枢纽点k，m到达需求点j的时间；Xijkm为0－1 变量，判断是否存在路径将物资通过枢纽k，m送至受灾点，存在则为1，否则为0；RTj为需求点j可接受的最晚物资到达时限；

然后，构建系统经济性函数F3，式（3）：

其中，Xik为0－1 变量，判断供应点i是否隶属于枢纽k，是则为1，否则为0；Xkj为0－1 变量，判断需求点j是否隶属于枢纽k，是则为1，否则为0；Xijkm为0－1 变量，判断是否存在路径将物资通过枢纽k，m送至受灾点，是则为1，否则为0；Yij为0－1 变量，判断供应点i是否直接向需求点j运输物资，是则为1，否则为0；dij为从供应点i到需求点j之间的距离；dik为从供应点i到枢纽点k之间的距离；dkm为从枢纽点k到枢纽点m之间的距离；dmj为枢纽点m到需求点j之间的距离；Cij为供应点i与需求点j两地之间的单位运输成本；Cik为供应点i与枢纽点k两地之间的单位运输成本；Ckm为枢纽点k、m两地之间的单位运输成本；Cmj为枢纽点m与需求点j两地之间的单位运输成本；αkm为经过枢纽点k，m运输的干线折扣率；uk为枢纽点的单位装卸费用；

最后，进行约束条件设置：

判定是否存在物资运输从供应点i经过枢纽点k、m最终到达需求点j，式（4）：

其中，Xkk为0－1 变量，判定枢纽点k是否被选作中转枢纽，是则为1，否则为0。

运输方式只有转运和直达两种运输方式，式（6）：

一个供应点i只能被分配给一个枢纽点，式（7）：

一个需求点j只能被分配给一个枢纽点，式（8）：

只有枢纽k被选作枢纽点才能为供应点i服务，式（9）：

只有枢纽k被选作枢纽点才能为需求点j服务，式（10）：

表示运输决策直达的判定方式，式（11）：

其中，v为运输工具的运输速度；v1为公路运输；v2为铁路运输。

物资从供应点i最终到达需求点j的时间，分为3 种：经过两个不同枢纽点k、m到达需求点j，经过一个枢纽点k到达需求点j，直接到达需求点j，式（12）：

其中，rk为在枢纽k的单位货物进行中转的时间。

供应点i给需求点j的物资供应量满足需求点j的最低物资满足量，e为紧迫度分级后的最低满足率，式（13）：

式中：e为需求点的最低满足率，I 类需求点的最低满足率e1＝0.7，II 类需求点的最低满足率e2＝0.6，III 类需求点的最低满足率e3＝0.5。

需求点j的物资满足量不超过其需求量，式（14）：

供应点i的供给量不超过其可供应量，式（15）：

其中，qi为供应点i可供应物资量。

2.2 需求紧迫度评价指标体系构建

由于重大传染病疫情的突发性和扩散性，需要快速进行疫区救援。 而在疫情初期，医疗应急物资、应急救援人员及运输工具等资源往往无法满足所有需求点的需求，加之需求点之间存在感染情况和医疗水平的差异性，需求点对于物资需求量和时间也有区别。 为了保障疫区的各需求点的公平性，需要考虑各需求点之间的差异，综合评价需求点的应急物资需求紧迫度，在资源供应不足的情况下最大化有限的应急物资的效用，更好地控制疫区疫情扩散。

需求紧迫度评价指标一般包括受灾人员的数量、基础设施的损坏程度及物资储备等情况，本文结合传染病疫情选取潜在扩散风险、疫情感染情况、城市自救能力这3 个关键因素作为的一级指标，并在每个一级指标下选取多个二级指标，构建需求点紧迫度评价指标体系见表1。

表1 需求点紧迫度评价指标体系Tab. 1 Evaluation index system for the urgency of demand points

2.3 基于熵值－TOPSIS 确定需求紧迫度

熵值法是一种客观评价方法，根据数据本身的信息来确定客观权重，可以避免人为主观因素导致的偏差［12］。 TOPSIS 法是对方案进行多目标决策的常用方法，通过比较目标方案与正负理想解的距离进行方案排序［13］。 本文通过熵值法确定各评价指标的权重，并通过TOPSIS 法对需求紧迫度系数进行计算，熵值－TOPSIS 法的计算步骤如下：

2.3.1 熵值法

步骤1建立指标矩阵

将m个需求点的n个影响因素指标数据处理成矩阵Xij代表第i个需求点的第j个影响因素指标数据的值（i≤12，j≤7）；

步骤2数据标准化

为了消除数据的量纲影响，需要对数据进行标准化处理，本文涉及两种类型的数据：效益型指标和成本型指标。 效益型指标代表其指标与评价结果正相关，式（16）：

成本型指标代表其指标与评价结果负相关，式（17）：

步骤3计算第j项指标下第i个需求点占该指标的比重Pij，式（18）：

步骤4计算第j个指标的熵值Ej，式（19）：

步骤5计算差异系数Gj，式（20）：

步骤6确定各项评价指标的权重Wj， 式（21）：

2.3.2 TOPSIS 法

步骤1对评价指标矩阵进行归一化处理，rij为归一化后各指标的值，式（22）：

步骤2将rij与熵值法得到的权重Wj进行加权操作得到vij，式（23）：

步骤3计算正理想解A＋， 负理想解A－， 式（24）和式（25）：

步骤4计算各需求点j到正理想解的距离，到负理想解的距离Di－，式（26）和式（27）：

步骤5计算各需求点i的相对贴近度Ci，该结果作为需求点的紧迫度值，式（28）：

3 改进NSGA－II 算法

本文考虑的需求紧迫度的应急物资供需网络模型是一个高复杂度、多约束、多目标的优化问题，属于NP－Hard 难题，对于此类问题传统的精确算法难以获得理想的结果。 NSGA－II 算法是在遗传算法（GA）的基础上通过增加快速非支配排序、拥挤度距离比较和精英保留策略，是经典的已被广泛应用于解决多目标问题的方法［14］。 但是传统的NSGA－II算法在种群分布性和多样性有所缺陷，因此本文采用改进的NSGA－II 算法（Improved Non－dominated Sorting Genetic Algorithms，INSGA－Ⅱ）求解该模型。修改拥挤度距离计算，增加种群分布性，增加外部存档对全局非支配解进行存储，保留解的多样性，并通过K－means 聚类方法对外部存档进行聚类操作，从而有效地提高了算法的性能。 INSGA－Ⅱ算法流程图如图2 所示。

图2 INSGA－Ⅱ算法流程图Fig. 2 INSGA－II algorithms flow chart

3.1 染色体编码

根据轴辐式应急物资供需网络模型的特点，对其进行编码设计。 一条染色体由3 个子串组成，每条染色体表示一个可行解。 子串1 采用实数编码，长度为i∗j，表示供需网络中供应点i向需求点j的实际物资供给情况；子串2 采用0－1 整数编码，长度为i∗j，代表供需网络各路径的转运／直达判别，1 代表转运，0 代表直达；子串3 采用实数编码，长度为i＋j，表示供应点i和需求点j被分配给枢纽点k的情况；染色体的总长度为2∗i∗j＋i＋j，示意如图3 所示。

图3 染色体编码示意图Fig. 3 Schematic diagram of chromosome coding

3.2 改进拥挤度距离

传统拥挤度距离计算方法可以使得种群呈现均匀性，但是对于目标函数差异性较大的个体不易获得遗传下去的机会，从而不利于种群的分布性。 因此，构建拥挤度距离方差公式，如式（29）所示：

其中，代表第i＋1 个个体在第m个目标函数的值，代表与第i＋1 个个体相邻的第i －1 个个体在第m个目标函数的值。

3.3 添加外部存档

在每一次迭代结束后都会产生一组新的非支配解，因此，添加外部存档将当前种群中所有标记为非支配的个体进行存储，从而将全局的非支配解进行保存，使得其更逼近真实的帕累托前沿。 对于外部存档的更新规则如下：

（1）将当前种群中所有标记为非支配的个体添加到外部存档中进行存储，这些个体是当前种群中的非支配解；

（2）对外部存档进行去重操作，确保其中不包含重复的个体；

（3）对外部存档中的所有个体进行非支配排序，将其分为不同的层次；

（4）从所有非支配层中选出最好的一层，作为新的非支配解集。 这个过程中，只有标记为非支配的个体才会被保留，其他个体都将被删除。

3.4 K－means 聚类全局非支配解集

外部存档存储了全局的非支配解，其存储的非支配解过于庞大，K－means 是经典的数据聚类算法［15］。 本文使用K－means 聚类对外部存档进行选择，该操作的步骤如下：

（1）从外部存档中提取出所有个体的目标函数值，并将其归一化到［0，1］的范围内，在保留3 个目标函数分别最大的3 个解以外，随机从剩下的解集中选择97 个解，每个解代表一个聚类中心Ci；

（2）对于剩下的每个解，根据解xj与聚类中心Ci的欧氏距离，将每个解分配到与其最相似的聚类中，该距离计算公式如式（30）所示：

其中，m为空间维度，本文每个解有3 个目标函数，因此m＝3。

（3）计算每个聚类的新中心；

（4）迭代步骤2 和步骤3，直到目标收敛；

（5）在每个聚类中找到最靠近质心的解，并使其成为该聚类的代表解，并将解集输出。

4 算例分析

4.1 案例背景与参数设置

传染病疫情爆发初期，各市应急医疗物资严重短缺，全国各地的物资在政府的统筹调度下前往湖北省各疫区。 本文以湖北省12 个市级作为需求点，选取北京南站、上海虹桥站、成都东站、西安北站、郑州火车站、南京火车站、重庆北站、杭州东站这8 个国内规模较大设施完善的火车站作为备选枢纽点，并将其编号为1～8。 根据疫区范围及地理位置，选取9 个国家应急物资储备库作为应急物资供应点。各两地之间的行驶距离通过百度地图进行查询。 评价指标体系中各数据通过湖北省统计局2020 统计年鉴（http：／ ／tjj.hubei.gov.cn／）和湖北省卫生健康委员会（http：／ ／wjw.hubei.gov.cn／）获得，评价指标体系中各级指标数据见表2；物资需求点的防疫物资口罩的需求量依据易感人群2 个／人／天，感染患者依据专家建议4 小时需更换一次口罩，设定为6 个／人／天的配比预估需求量，湖北省各市需求量见表3；依据各物资储备库规模预估现阶段应急物资库存量见表4；按照需求点应急物资紧迫度评价指标计算得出各需求点的需求紧迫度见表5，并根据紧迫度评价结果对物资最低满足量进行分级，I、II、III 级的物资最低满足量分别为0.7、0.6、0.5。 根据中国人民共和国国家发展改革委（https：／ ／www.ndrc.gov.cn／）中的国家铁路货物统一运价，将本文铁路运输成本定为0.115 元／tkm；根据公路运输价格相关规定及各公路运输公司定价数据，本文将公路运输成本设定为0.45 元／tkm。 定义公路运输速度60 km／h，铁路运输速度100 km／h，枢纽点选择数量为5 个，需求点能接受的最晚到达时间RTj为24 h，干线折扣率αkm为0.6。

表2 评价指标体系各级指标数据Tab. 2 Data of indicators at all levels of the evaluation index system

表3 需求点物资需求量Tab. 3 Material requirements of different regions

表4 供应点物资库存量Tab. 4 Material storage of different regions

表5 需求点的需求紧迫度Tab. 5 Urgency of different regions

INSGA－II 算法的参数设置：种群规模popsize＝100，最大迭代次数maxgen＝2 000，交叉概率pc＝0.8，变异概率pm＝0.1。

4.2 算法对比

通过将NSGA－II 算法与INSGA－II 算法各自独立运行10 次，结果均能得到帕累托前沿解集，为了进一步评价算法的性能，引入评价指标Spacing ，Spacing 是衡量算法解集分布性的指标，其值越小，表明算法越好， 两个算法各自独立运行10 次，算法性能Spacing 指标箱型图结果如图4 所示。 INSGAII 算法的平均值低于NSGA－II 算法，表明INSGA－II算法在求解本文模型的帕累托前沿解集在解空间内具有更好的分布性和延展性；其次INSGA－II 算法的箱体比NSGA－II 算法要窄，这表明INSGA－II 算法具有更好的稳定性。

图4 算法性能Spacing 指标箱型图Fig. 4 Box plot of Spacing metrics algorithm perform

4.3 结果分析

本模型的运算结果如图5 INSGA－II 的帕累托前沿解集所示。 其中，3 个维度的坐标分别表示物资分配公平性F1、物资运输有效性F2、系统总成本F3。 由于目标之间存在一定的冲突性，最终方案的抉择取决于决策者的偏好。 例如：在突发事件初期，更低的物资缺口是主要考虑的因素，可以选择目标函数1 在帕累托前沿上表现最好的方案；在突发事件中后期，相关单位对疫情防控有了一定的把控时，期望在经济性上有更好的体现，可以选择目标函数3 在帕累托前沿上表现最好的方案。 图5 中的点需求缺口最小、点时间延误最小、点系统总成本最小这3 个点分别为3 个目标各自最优时的方案。 决策者也可以为目标函数赋权，从而得到一个综合性的解，由于前期低缺口的重要程度较高，可以接受一定的时间延误，以及弱经济性原则，从而将权重设定为1／2、3／10、2／10，得到综合性赋权方案，并将这4 个方案标注在图5 上。 这4 个方案的3 个目标函数值见表6。

表6 4 个方案的目标函数值Tab. 6 Objective functions of the four programs

图5 INSGA－II 的帕累托前沿解集Fig. 5 INSGA－II Pareto frontier solution set

这4 种方案代表不同的决策偏好，一个目标函数的提升，会牺牲其他目标函数，因此在实际决策过程中，可以根据现实情况对这3 个目标函数的偏好从帕累托解中选择合适的方案。 赋权综合性方案的调度，需求点的物资实际分配数量见表7，运输方式见表8。 通过表7，表8 可以直观看到所有物资的运输路径，如北京供应点向武汉需求点从枢纽点1 北京南站和枢纽点5 通过公铁联运向郑州站运输物资38 t，南宁供应点向武汉需求点通过公路直达运输物资11 t。

表7 需求点的物资实际分配数量（t）Tab. 7 Actual quantity of materials allocated at the point of demand （tons）

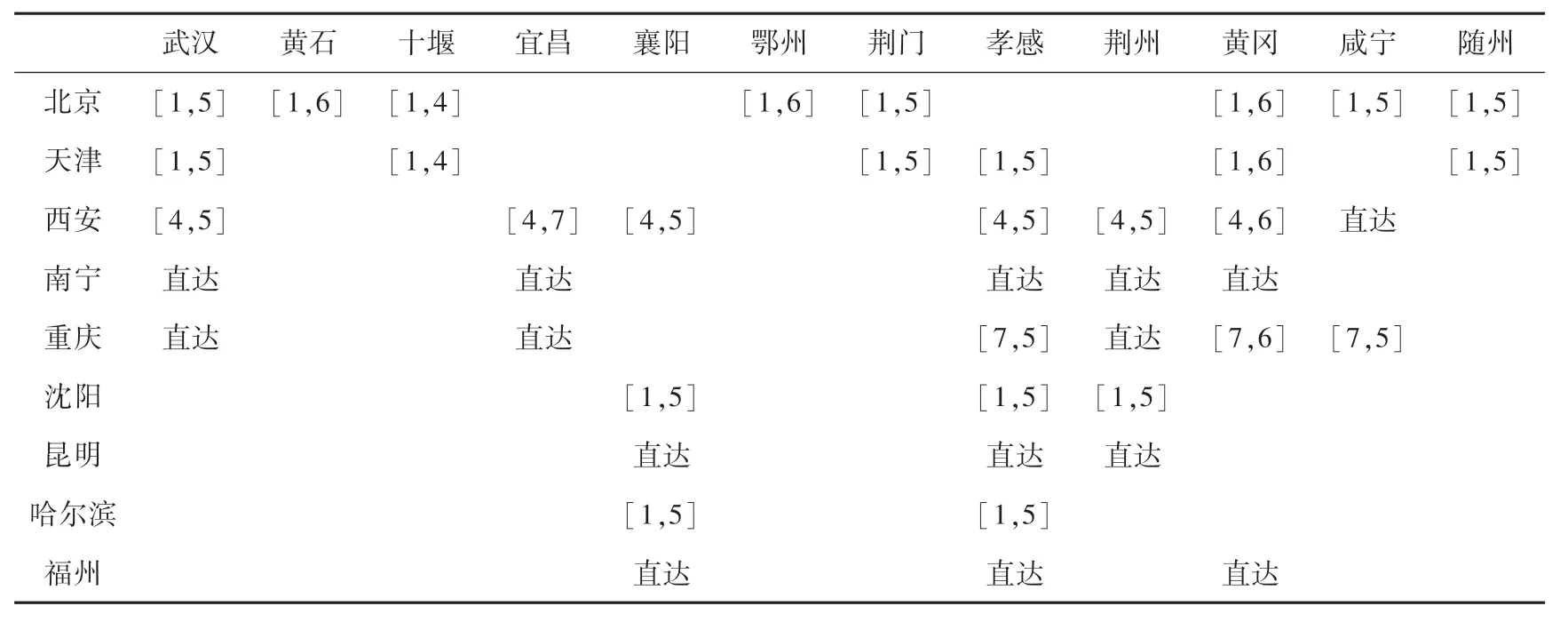
表8 应急物资调度方案的运输方式Tab. 8 Transportation mode of material dispatch program

为进一步验证模型对公平性的有效性，模拟不考虑紧迫度和不考虑轴辐网络的模型，使用INSGA－II 算法对两个模型求解，本文选取两个模型中的相同权重下的综合赋权方案进行对比，方案A 表示本文考虑紧迫度和采用轴辐网络模型的方案，方案B表示不考虑紧迫度和不考虑轴辐网络模型的方案。方案A 的物资满足率如图6 所示，方案B 的物资满足率如图7 所示，方案间的时间延误对比如图8 所示，方案间的成本对比如图9 所示。

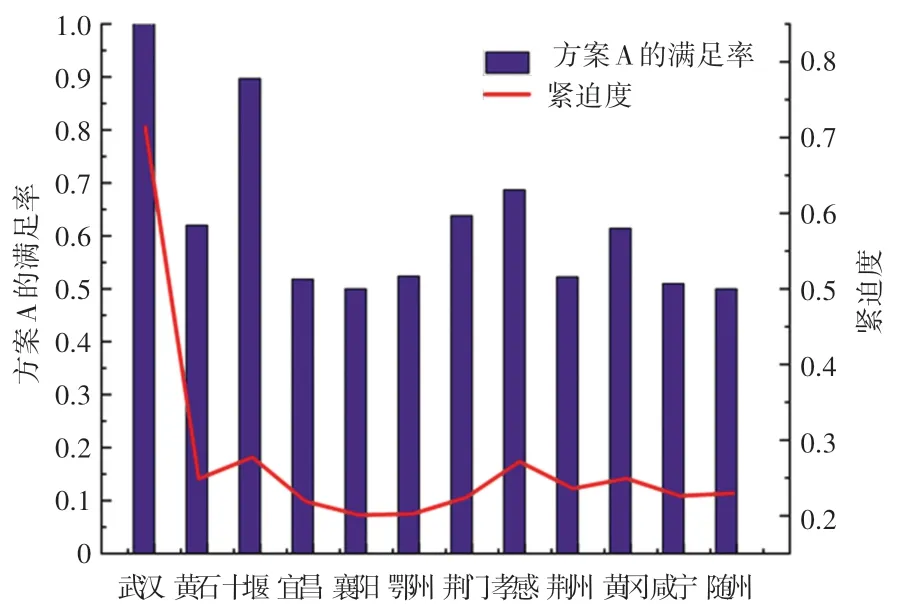
图6 方案A 的物资满足率Fig. 6 Material satisfaction rate for program A

图7 方案B 的物资满足率Fig. 7 Material satisfaction rate of program B

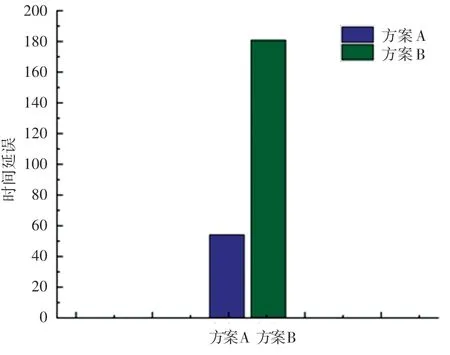
图8 方案间的时间延误对比Fig. 8 Comparison of time delays between programs

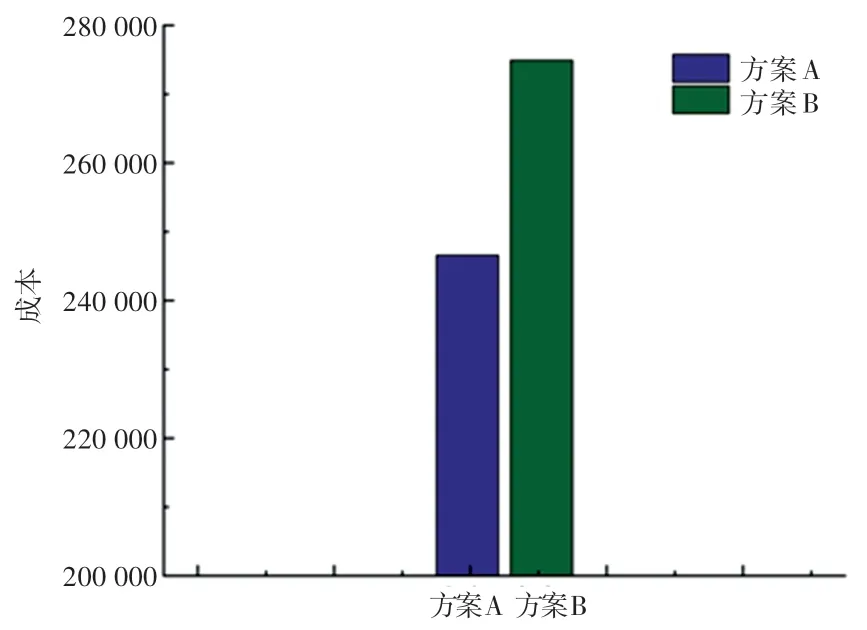
图9 方案间的成本对比Fig. 9 Comparison of time cost between programs

由图6－图9 可知：本文得出的方案（方案A）考虑紧迫度，其对物资分配的公平性大于不考虑的方案（方案B），其时间延误和成本也小于方案B，这表明本文构建的考虑紧迫度的轴辐应急物资供需网络是可行的。 在方案B 中，物资满足率最高的城市是十堰、襄阳和随州，这3 个城市的物资满足率在98%～100%，基本完全满足需求，而疫情最严重的武汉物资满足率仅有65%，对于突发公共卫生事件的应急物资分配而言是不合理的。 而在方案A 中，作为紧迫度最高的城市武汉，获得了所有需求点中最高的物资满足率100%，这是因为本模型通过衡量需求点间的差异性，使得优先对最紧迫的城市进行物资分配，从而保障了紧迫度高的城市的物资充足供给。 其次，从时间延误和成本的角度来看，方案A的表现均比方案B 好，是因为轴辐网络通过选择时间更短成本更低的轴点间铁路运输，有效地提升了调度效率。

5 结束语

本文针对突发公共卫生事件下的应急物资调度问题，构建了考虑需求紧迫度的以需求缺口最小、时间延误最少和系统总成本最小为目标的应急物资轴辐供需网络优化模型。 首先，结合应急物资调度的特点，构建需求紧迫度评价指标体系，并使用熵值－TOPSIS 法对需求点紧迫度进行求解；其次，基于轴辐结构在轴点间的规模运输能力，对传统调度供需网络进行改进，提出基于轴辐结构多式联运的应急物资供需网络模型；最后，基于模型设计改进的NSGA－II 算法，INSGA－II 算法对拥挤度进行改进，添加外部存档对全局非支配解进行存储，并对外部存档进行K－means 算法聚类。 通过对实例的结果分析，发现模型可以求解出有效的帕累托前沿解集，并相比于不考虑紧迫度和不考虑轴辐结构的模型，本模型的物资调度具有更好的公平性，并在时间延误和成本上更优。 为了更贴近实际应急物资调度情况，后续研究将进一步考虑轴点的容量限制，同时考虑多品类应急物资、多阶段的动态调度。