基于社会学习粒子群的大规模多目标优化算法

刘能现

（福州大学研究生院， 福州 350116）

0 引 言

多目标优化问题（Multi－Ojective Optimization Problems，MOPs）广泛存在于工程实践和科学研究中。 如：社区检测［1］、云工作流调度［2］和车辆路径问题［3］等。 多目标优化问题通常含有2 个及以上的目标，且这些目标之间相互冲突。 过去的几十年，关于多目标优化问题的研究取得了很大发展，研究人员提出了大量的多目标进化算法（Multi－Objective Evolutionary Algorithms， MOEAs），这些算法大致可以分为Pareto 支配多目标算法（如NSGA－II），基于分解的多目标算法（如MOEA／D），基于指标的多目标算法（如IBEA），及其它不属于前3 类的算法（如MOEA／DD）等等。 近年来，大多数关于多目标进化算法的研究主要集中在高维多目标优化问题上，而对于决策变量较多的多目标优化问题关注较少。 然而，现实世界中很多多目标优化问题可能有数百甚至数千个决策变量，这类问题被称为大规模多目标优化问题（Large－Scale MOP， LSMOP）［4］。

通常，大规模MOP 比决策变量少的MOP 更难解决，其主要原因是MOP 的搜索空间与决策变量的数量呈指数关系，即维度灾难问题，使得大多数现有多目标进化算法无法有效地探索搜索空间，并可能会过早地收敛到局部最优值或收敛到太大的区域［5］。 尽管大规模单目标优化问题多年来一直是热门研究课题，但大规模多目标优化的研究仍处于早期阶段。 一般来说，现有的求解大规模多目标问题的进化算法可以大致分为3 类［6］：

（1）基于决策变量分组算法

该类算法在求解大规模优化问题时使用分治策略，将决策变量随机或启发式地分成几组，然后交替优化每组决策变量。 该策略已广泛用于解决大规模的单目标优化问题，但大规模的多目标优化问题包含多个相互冲突的目标，决策变量之间的相互关系更加复杂，在决策变量分组与优化时，应考虑总体的收敛性和多样性。 现有MOEA 中的决策变量分组技术主要包括随机分组、差分分组和变量分析。 如：CCGDE3［7］算法使用随机分组策略，将决策变量随机划分为大小相同的分组。 虽然该算法在一些优化问题上取得了较满意的优化结果，但由于没有考虑变量之间的相互关系，在处理具有复杂变量关系的大规模多目标优化问题时效果较差。 Ma 等人［8］提出了一种基于决策变量分析的大规模多目标优化算法MOEA／DVA。 该算法根据收敛性和多样性把决策变量分成位置相关变量、距离相关变量和混合变量，在解决某些大规模多目标优化问题时具有较好的效果，但需要大量的适应度评估进行变量分析。Zhang 等人［9］进一步扩展了MOEA／DVA 算法，提出了LMEA 算法。 该算法根据角度，把决策变量分为收敛性相关决策变量和多样性相关决策变量。

（2）基于决策空间缩减算法

该类算法用降维的思想，将父代的决策向量维数缩短并用于生成后代，然后将缩短的后代向量恢复到原始决策空间进行函数评估。 因此，该类算法只需要找到一个短向量的最优值，而不是在高维决策空间中搜索。 目前降维的技术主要包括问题转换、问题重构、随机嵌入、主成分分析等。 如：Zille等人［10］提出了一种加权优化框架（WOF），该框架对原优化问题通过变量分组和加权实施转换。 其主要思想是采用分组策略将决策变量划分成几组， 每组变量关联一个权重， 即在同一组内的变量具有相同的权重， 从而将大规模决策变量的优化转化为对维度较低权重向量的优化， 实现对原搜索空间的降维，但该方法在重构解时较依赖于分组策略。 He 等人［11］提出采用问题重构优化框架LSMOF，其核心思想是通过问题重构直接跟踪Pareto 最优解。 基于LSMOF 的思想，Qin 等人［12］提出了一种大规模多目标优化方法LMOEA－DS，该方法在搜索方向上直接生成解。

（3）基于新搜索策略算法

该类算法通过设计新颖搜索策略直接在原搜索空间生成后代，来求解大规模多目标优化问题。 这类算法只需设计相对简单的操作就能在不同的大规模多目标优化问题取得较好的性能。 新的搜索策略主要包括新的生成后代的操作算子、概率模型等。 如：Tian 等人［4］提出一种基于竞争学习粒子群的大规模多目标优化算法LMOCSO。 在该算法中，作者提出一种考虑速度和加速度的新策略。 其中，失败粒子向获胜粒子学习，使失败粒子能更有效地向更好的位置移动。 Cheng 等人［13］提出了一种基于概率模型的大规模多目标优化算法IM－MOEA，该算法通过构建基于高斯过程的逆模型，将解从目标空间映射到决策空间，并使用逆模型对目标空间进行采样来生成后代。

尽管现有的大规模多目标优化算法都有良好的性能，但每一类算法也有其自身的不足。 如基于决策变量分组的方法，在求解复杂景观的多目标优化问题会遇到困难。 具体来说，基于决策变量分组的MOEA，可能会将两个相互关联的变量分到不同的组，因此在分别优化这两个变量时，算法很可能陷入局部最优。 对于基于决策变量分析的MOEA，虽然能够检测变量间的相互关系，但该操作需要大量的函数评估。 基于决策空间缩减的算法，可以快速找到大规模多目标优化问题的一些局部最优解，但即使消耗更多的函数评估，其也可能无法找到全局最优解，这是因为转换后的问题很可能会丢失原始大规模多目标优化问题的全局最优解［6］。 基于新搜索策略的算法一般需要较多函数评估次数才能获得问题解［12］，但新搜索策略一般独立于选择策略，其可以比较容易地嵌入到许多MOEA 中，以提高其在处理大规模多目标优化问题上的性能。

受基于竞争机制粒子群的大规模多目标优化算法的启发，本文基于社会学习的粒子群算法，提出了一种处理大规模多目标优化问题的算法LMOSLPSO。 通过实验对比发现，该算法比其它几个大规模多目标进化算法有更好的性能表现。

1 相关概念

1.1 多目标优化问题

不失一般性，求最小值问题的多目标优化问题可描述如下：

其中，x＝（x1，x2，…，xD） 表示决策空间的D维向量；m为目标个数；fi（x）；i＝1，2，…，m是m维目标空间中的目标函数；gp和hq分别表示k个不等式约束和l个等式约束。

给定两个可行解xa和xb，xa支配xb，当且仅当对于∀i，fi（xa） ≤fi（xb） 和∃j，fj（xa）＜fj（xb），i，j∈｛1，2，…，m｝ 。 如果没有其他解支配x∗， 那么x∗称为帕累托最优解。 所有的帕累托最优解构成帕累托最优解集（Pareto optimal Set，PS），其目标值构成帕累托前沿（Pareto Front，PF）。

带2 个最小化目标的优化问题如图1 所示。 其中，x3支配x1和x2，x1和x2之间互不支配，蓝色曲线上的点为帕累托最优解，蓝色曲线为帕累托前沿。

图1 带2 个最小化目标的优化问题Fig. 1 Optimization problems with two minimization objectives

1.2 基于社会学习的粒子群算法

为求解单目标优化问题， Kennedy 等于1995 年提出粒子群优化算法（PSO），该算法在求解决策变量规模较小的问题时有较好的效果。 但是，随着问题规模的增大，PSO 算法在搜索过程中较难平衡算法收敛性以及种群多样性，而且粒子在算法搜索的后期容易早熟收敛，陷入局部极值。 为此，Cheng 等人［14］在2015 年提出了一种改进的粒子群算法来求解大规模单目标优化问题，并将其称为基于社会学习的粒子群算法（SLPSO）。

在SLPSO 算法中，首先按适应值大小对种群中的粒子进行排序，然后种群中除最优粒子外的其它粒子以一定的概率向其它较好的粒子及种群的平均位置学习。 具体学习方式由公式（2）、（3）定义。

其中：

式中：v、x和g分别表示粒子的速度、位置和进化代数，r1，j、r2，j和r3，j均为区间［0，1］ 内的随机数，为社会影响因子，用来调节算法的多样性和收敛性，其中β＝0.01，M＝100，k表示粒子i在j维上学习粒子（示范粒子），k选择过程如图2 所示，为当前种群在第j维上的平均值，ps为种群大小。

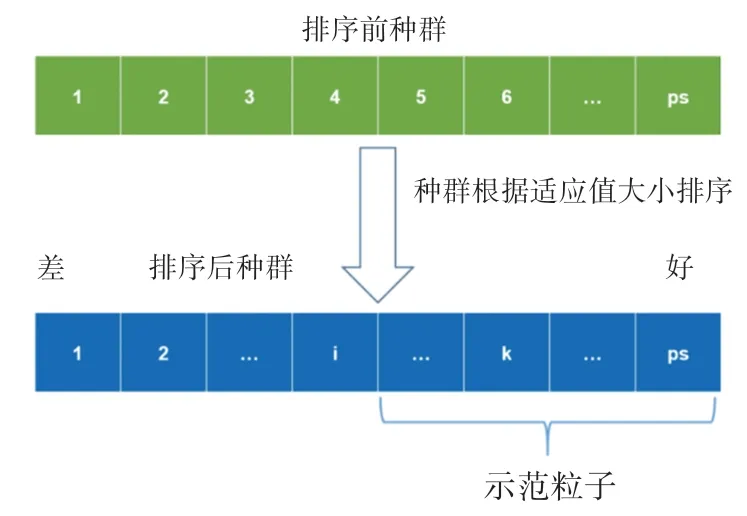
图2 种群排序和选择示范粒子kFig. 2 Population sorting and selection of demonstration particle k

2 基于社会学习粒子群的大规模多目标算法

2.1 算法框架

图3 LMOSLPSO 算法的框架图Fig. 3 The framework of LMOSLPSO algorithm

算法1LMOSLPSO 框架

初始化：种群大小ps，问题维数D，最大函数评估次数FESmax，函数评估次数FES，随机初始化种群P；

while（FES ＜FESmax） do

P′←基于社会学习的粒子群进化（P）；

P←环境选择（P，P′）；

end

输出P中的所有非支配个体

二是全面性原则。量化评审指标设置要尽可能全面完整、相互衔接，指标之间在内涵与外延上不能彼此交叉，互相重复。因此，在确定量化指标和评分标准时，要坚持从学历资历、能力水平、业绩成果等各方面对专业技术人员进行全方位评价。并要根据不同专业性质、岗位特点和技术复杂难易程度等，研究制定有针对性的、各有侧重的评价指标体系，科学合理确定各级指标分值和权重。量化评价体系既要综合评价参评人员各方面的能力，又要便于申报者之间进行比较，科学区别，保证优秀人才优先晋升。

2.2 基于社会学习的粒子群进化

基于社会学习的粒子群进化主要包括粒子的适应值计算、种群P 的排序及学习概率设置、粒子的速度和位置更新，以及所有粒子的多项式变异操作等。 基于社会学习的粒子群进化操作的伪代码如算法2 所示。算法2基于社会学习的粒子群进化（P）输入当前种群P；

利用公式（6）计算种群P中每个粒子的适应值；

对种群P按适应值从大到小（好到差）进行排序；

按公式（7）计算种群P中每个粒子学习概率；

for 除最优粒子外的每个粒子xiinPdo

if（lpi ＞rand） then ／ ／学习率大于随机数

｛k，l｝ ←从［1，i］ 中随机选择两个粒子；

使用公式（8）更新粒子速度vi；

使用公式（3）更新粒子位置xi；

end if

end for

对所有粒子执行变异操作并放入后代种群P′

输出后代种群P′首先，进行粒子的适应值计算，与单目标优化问题不同，因多目标优化问题含有多个目标且各个目标之间相互冲突，无法采用单个目标值直接进行粒子优劣的比较，为此需要一个能够评价粒子优劣的方法。 本文采用转换的密度估计策略（Shift－based Density Estimation，SDE）［16］来求解每个粒子的适应值。 SDE 策略能够从多样性和收敛性两个方面进行粒子的质量评价，并已被多个MOEAs 所采用［4］。因此，在LMOSLPSO 算法中，本文也采用了基于SDE 的策略来评估种群中每个个体的收敛性和多样性。 具体来说，用最小的基于SDE 的距离公式（6）［16］来定义粒子x的适应值。

按社会学习粒子群的思想，对种群P中的粒子按适应值从大到小进行排序，并按公式（7）计算每个粒子的学习率lpi，即为粒子排序值i除以种群数ps，表示越差的粒子越有机会向好的粒子学习。

接着对每个粒子按学习概率进行速度更新和位置更新。 具体来说，随机产生0 到1 之间随机数rand，当学习率大于随机数rand时，从种群中随机选择比粒子i具有更好适应值的两个粒子k、l，并按公式（8）更新粒子速度和按公式（3）更新粒子位置。本文的速度更新公式（8）与公式（2）不同，由于在多目标优化中，使用相同的种群平均位置引导种群会使种群失去多样性，因此本文利用了两个适应值较好的粒子来引导种群进化。

最后，为进一步提高LMOSLPSO 算法性能，避免算法陷入局部极值，对种群中的每个粒子执行多项式变异操作［17］。 在基于社会学习的粒子群进化结束后返回到算法1，执行多目标环境选择操作。

3 实验结果与分析

3.1 对比算法及测试函数

为验证LMOSLPSO 算法的效果，将其算法与多个经典的多目标算法进行对比。 其中包括：LMEA［9］、IM－MOEA［13］、MMOPSO［18］和LMOCSO［4］。

实验采用大规模多目标测试集［19］作为测试问题，即LSMOP1－LSMOP9。 LSMOP 测试集是在大规模单目标问题基础上设计的，该测试集的问题具有较好的可扩展性和普遍性。 在这9 个LSMOP 问题中，在Pareto 集上存在线性变量连接（如LSMOP1－LSMOP4） 和非线性变量连接（如 LSMOP5 －LSMOP）， 以及线性Pareto 前沿（如LSMOP1 －LSMOP4）、凹Pareto 前沿（如LSMOP5－LSMOP8），和非连续Pareto 前沿（如LSMOP9）。

3.2 评价指标

为了比较不同算法的性能， 本文采用反转世代距离（Inverted Generational Distance，IGD） 作为性能指标，来评价不同算法的实验结果。 假设目标空间中最优Pareto 前沿面上均匀分布的点集合为P∗，算法所求得的非支配解集为P，则IGD的计算公式定义为

其中，dist（x，y） 表示点x到点y之间的欧氏距离。 因此，反转世代距离IGD是从最优前沿面P∗中的每个点到支配解集P的平均最小距离，其测量的是支配解集P的收敛性和均匀性。IGD值越小，说明对应算法的综合性能越好。 同时，采用显著性水平为0.05 的威尔科克森符号秩检验对不同对比算法进行比较。

3.3 实验设置

本文实验采用Tian 等人［20］提出的PlatEMO 平台，所有算法采用Matlab 语言编程。 实验所用的电脑配置：中央处理器采用Inter（R）Core（TM）i5－4590 CPU＠3.30 GHZ，内存8.00 GB，操作系统Windows 7。

相关算法的参数参考文献［4］设置，所有对比算法种群大小设置相同；对于2 个目标的问题种群大小设置为300，3 个目标的问题种群大小设置为496。 对于LSMOP1 ～LSMOP9 问题，每个变量组的子分量数量nk设置为5，目标数M设置为2 和3，决策变量维数D的大小从100 到500 不等。 最大函数评估次数作为所有对比算法的终止条件，设置为15 000×D。

3.4 实验结果

不同算法在2 维多目标问题LSMOP1－ LSMOP9函数上IGD值的平均值和标准差详见表1，最好的IGD值用蓝色粗体字体标出。 从表1 中可见，本文提出的LMOSLPSO 算法对比其他4 种方法获得了更好的优化结果。 所提出的LMOSLPSO 算法在27 个测试问题中获得了17 个最优平均IGD值。 对比算法LMEA、IMMOEA、MMOPSO 和LMOCSO 分别在0、5、1和4 个测试问题上获得了最优平均IGD值。 具体来说，与LMEA 相比，本文提出的LMOSLPSO 算法在27个测试问题中的22（5）个测试问题上表现更好（相似）。 与IMMOEA 相比，LMOSLPSO 算法在27 个测试问题中的17（4）个测试问题上表现更好（相似）。与MMOPSO 相比，LMOSLPSO 算法在27 个测试问题中的21（1）个测试问题上表现更好（相似）。 与LMOCSO 相比，LMOSLPSO 算法在27 个测试问题中的19 （3） 个测试问题上表现更好（相似）。LMOSLPSO 算法具有更好的性能主要是因为其使用了基于社会学习的粒子群进化操作。

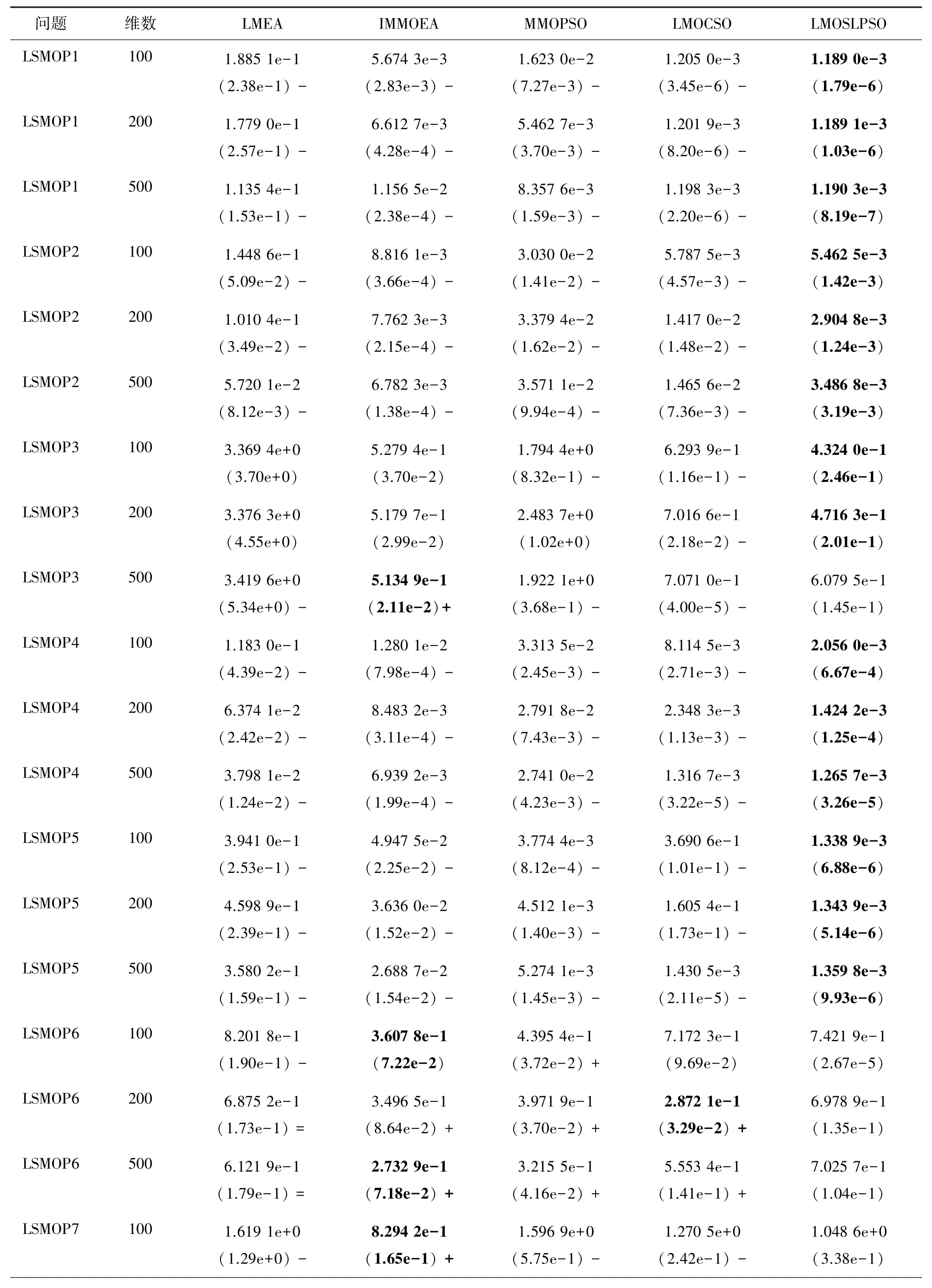
表1 不同算法在2 维LSMOP1－LSMOP9 上得到IGD 的平均值和标准差比较Tab. 1 Comparison of the mean and standard deviation of IGD obtained by different algorithms on 2－dimensional lsmop1－lsmop9

表2 给出了所有对比多目标算法在3 维多目标问题LSMOP1～LSMOP9 函数上的IGD值的平均值和标准差，最好的IGD值用蓝色字体标出。 从表2中我们同样可以清楚地看出， 本文提出的LMOSLPSO 算法比4 种对比方法获得了更好的优化结果。 所提出的LMOSLPSO 算法在27 个测试问题中的13 个上获得了最优平均IGD值，对比算法LMEA、IMMOEA、MMOPSO 和LMOCSO 分别在0、4、1 和9 个测试问题上获得了最优平均IGD值。 具体来说，与LMEA 相比，本文提出的LMOSLPSO 算法在27 个测试问题中的25（1）个测试问题上表现更好（相似）。 与IMMOEA 相比，LMOSLPSO 算法在27 个测试问题中的21（3）个测试问题上表现更好（相似）。 与MMOPSO 相比， LMOSLPSO 算法在27个测试问题中的22（5）个测试问题上表现更好（相似）。 与LMOCSO 相比， LMOSLPSO 算法在27 个测试问题中的11（10）个测试问题上表现更好（相似）。 在3 维多目标问题中，对比算法LMEA、IMMOEA 和MMOPSO 的对比性能有所下降，对比算法LMOCSO 的对比性能有所提高，但LMOCSO 的性能还是比本文提出的LMOSLPSO 算法的性能差。

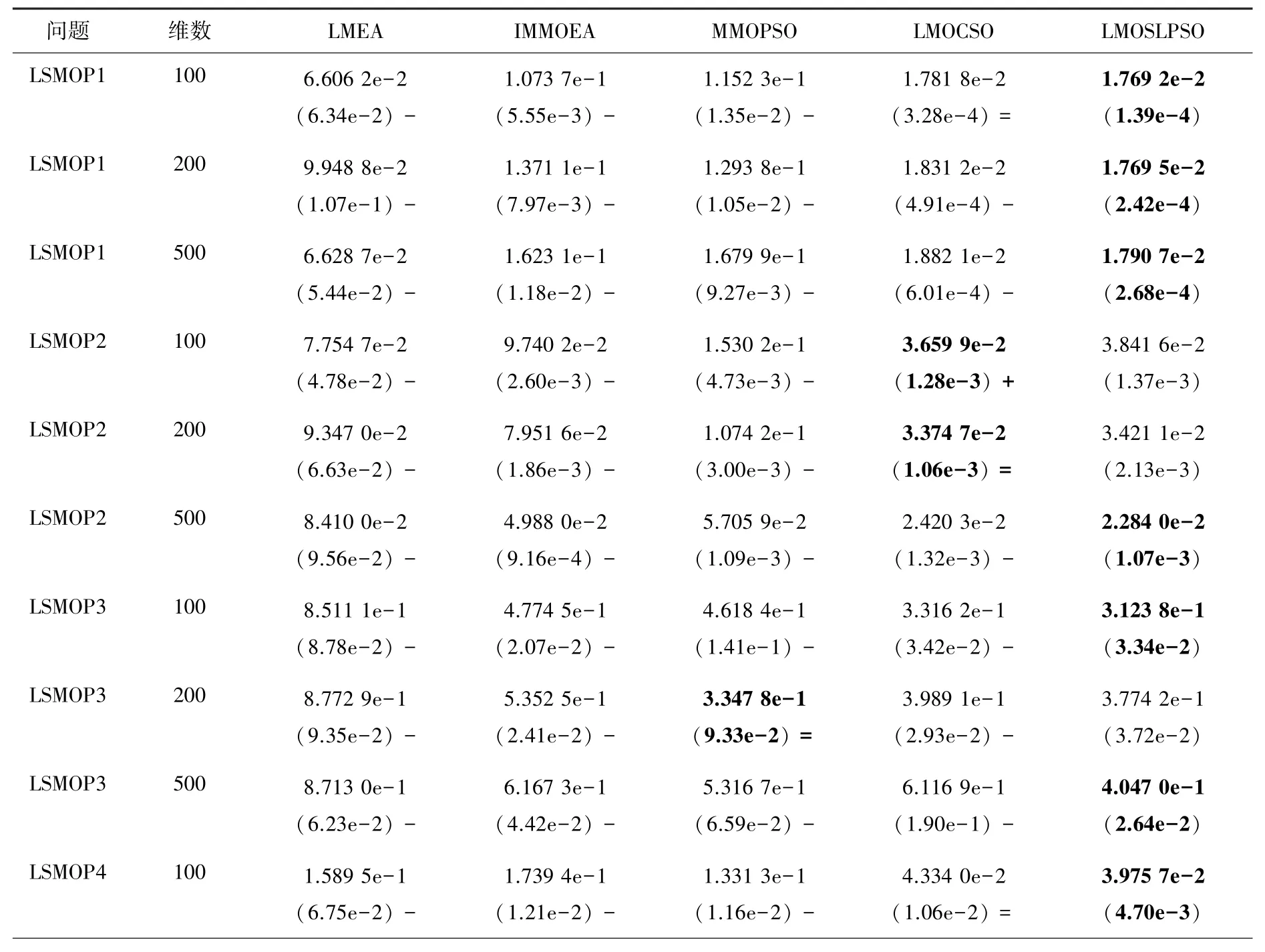
表2 不同算法在3 维LSMOP1～LSMOP9 上得到的IGD 平均值和标准差比较Tab. 2 Comparison of IGD mean and standard deviation obtained by different algorithms on 3－d lsmop1～lsmop9

图4 和图5 分别给出了所有对比多目标算法在2 维和3 维大规模多目标优化问题LSMOP4 上获得的非支配解。 由图中可以看出，对比算法LMEA、IMMOEA 和MMOPSO 获得的非支配解均匀性和收敛性较差。 从图4 可以看出，在2 维多目标优化问题LSMOP4 上，对比算法LMOCSO 和提出算法LMOSLPSO 均匀性和多样性都较好；从图5 可以看出，在3 维多目标优化问题LSMOP4 上，本文算法LMOSLPSO 在均匀性上比算法LMOCSO 更佳。

图4 不同算法在双目标LSMOP4 函数上获得的非支配解Fig. 4 The non－dominated solution obtained by different algorithms on the bi－objective LSMOP4 function

综上所述，从表1、表2 以及图4、图5 可以得出，本文提出的LMOSLPSO 算法比其它算法在求解大规模多目标优化问题上有较好的性能表现。

4 结束语

本文基于社会学习粒子群算法思想，提出了一种用于求解大规模多目标优化问题的多目标粒子群算法（LMOSLPSO）。 该算法利用转换的密度估计策略求解每个粒子的适应值，然后基于适应值排序设计了一种有效的粒子速度更新方法。 该方法能有效引导种群进化，使所提出的LMOSLPSO 算法获得了综合性能较优的优化结果。 实验结果表明，LMOSLPSO 算法比对其他算法有较好的性能表现，该算法是处理大规模优化问题的有效算法。