自编码器及其改进算法在滚动轴承故障诊断的应用
2023-06-21周建民刘露露杨晓彤王云庆
周建民,刘露露,杨晓彤,王云庆
(1.华东交通大学载运工具与装备教育部重点实验室,江西 南昌 330013;2.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室,江西 南昌 330013)
滚动轴承在各类旋转机械中被广泛应用,而且在决定设备运行状态方面起着重要作用。因此,对滚动轴承进行故障诊断和在线状态监测具有重要的现实意义[1]。在实现滚动轴承的故障诊断和在线状态监测的方法中,浅层机器学习的应用较多,但浅层机器学习的结构缺乏强大的表示能力,难以处理复杂非线性关系问题[2]。在这个情况下,深度学习作为研究领域中新的突破点,快速在各个领域中被广泛地研究与应用[3-4]。深度学习能自主学习隐藏在原始数据中的主要信息,并在数据和设备运行状态之间建立精确的映射关系[5],故而在各种诊断模型中,基于深度学习的应用与研究也日渐增多。
将深度学习方法应用在滚动轴承故障诊断领域的研究中,一般都会针对不同的问题来实行不同的学习方式,如有监督学习、无监督学习等。在有监督学习模式下,算法需要大量的有标签的训练数据,这就导致算法在一定程度上受到数据的约束,在这种情况下,无监督深度学习在滚动轴承故障诊断上的发展及应用逐渐被重视起来,自编码器(auto-encoder, AE)就是一种典型的无监督深度学习的网络模型。
自编码器的运行过程就是一个编码解码的过程,但是需要通过误差反向传播机制调整整体网络[6-7],近年来,基于AE 的研究与应用也越来越多[8-11]。Bengio等[8]提出在AE 的隐含层中引入稀疏性限制项的稀疏自编码器(sparse auto-encoder,SAE)这一改进网络,其目的旨在获得高维且稀疏的特征。Vincent 等[9]在AE 中引入添加噪声,提出了降噪自编码器(denoising auto-encoder,DAE)这一改进网络,从而减弱噪声影响,此外堆栈降噪自编码(stacked denoising auto-encoder,SDAE)网络是深度自编码网络的另一种形式,它只是用DAE 代替AE。因此,目前基于自编码器的滚动轴承故障诊断方面的应用主要有数据降维和数据降噪两个方面[12],可以通过Matlab、TensorFlow、Pytorch、Keras 等不同框架或平台实现。
本文将介绍AE、SAE、DAE、SDAE 等算法的网络结构及其理论理解,梳理自编码器改进算法的创新点与实现方式。同时,结合相关文献来总结上述几类自编码器在针对滚动轴承故障诊断的研究进展。最后,分析当前自编码器及其改进算法仍存在的问题,探讨解决这些问题的思路。
1 自编码器及其改进
在深度学习中,自编码器是一种典型的无监督网络模型,它在学习输入数据隐含特征的同时,还可以利用学习到的特征来重构原始输入数据,从而形成一种无监督模型的特征提取方法。
1.1 自编码器
AE 是一种典型的单隐层神经网络,它以无监督的方式学习参数并提取特征,使输入和输出保持一致性,从输入到隐含层和从隐含层到输出层的过程分别称为编码和解码,AE 的网络结构如图1 所示。
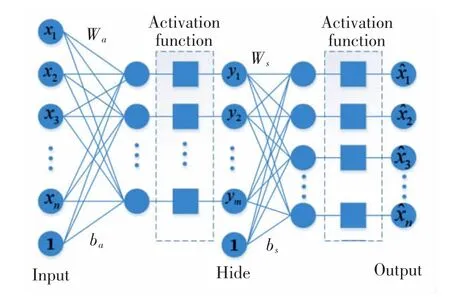
图1 AE 网络结构图Fig.1 AE network
如图1 所示,自编码器通过全连接的方式将输入信号进行加权求和,经过偏置矩阵与激活函数计算后输入到隐含层,而隐含层也以同样的相同方式输入到输出层中,最后通过设置目标函数来得到最优的权值和偏置。自编码器的计算公式如下
常规自编码器一般采用反向传播算法来优化调整网络的权值和偏置,从而使更新后的网络输出样本更加接近输入样本,同时还能提取出更具样本表征的抽象特征。
与一些无监督学习算法相比,AE 不仅能降低提取的特征维度,还保存了更多的信息表示度,它可以综合地利用各种特征信息来进行数据降维和特征提取,因此可以更有效地实现滚动轴承的故障分类任务。
目前,自编码器已成为故障诊断领域的一个热点[13-14]。Mao 等[15]结合自编码器和极限学习机的方法提出一种新的算法,实现了自适应挖掘识别滚动轴承故障特征并且提高了诊断速度。张西宁等[16]将标准化的自编码网络运用到滚动轴承故障诊断,通过实验证明该网络不仅可以提高网络在噪声环境下的识别能力, 而且能够有效地减少网络的训练时间。Pei 等[17]针对数据不平衡问题提出了一种增强少镜头瓦瑟斯坦自编码器的数据增强方法,结果表明该模型在不平衡程度的恢复能力方面非常优异,且具有较好的精度。
1.2 降噪自编码器
DAE 在自编码器的基础上进行了改进,在编码过程中以随机置零神经元的方式来添加噪声,然后再进行后续的解码过程。DAE 通过这样的方式来增强网络泛化能力,并降低噪声影响,其网络结构如图2 所示。
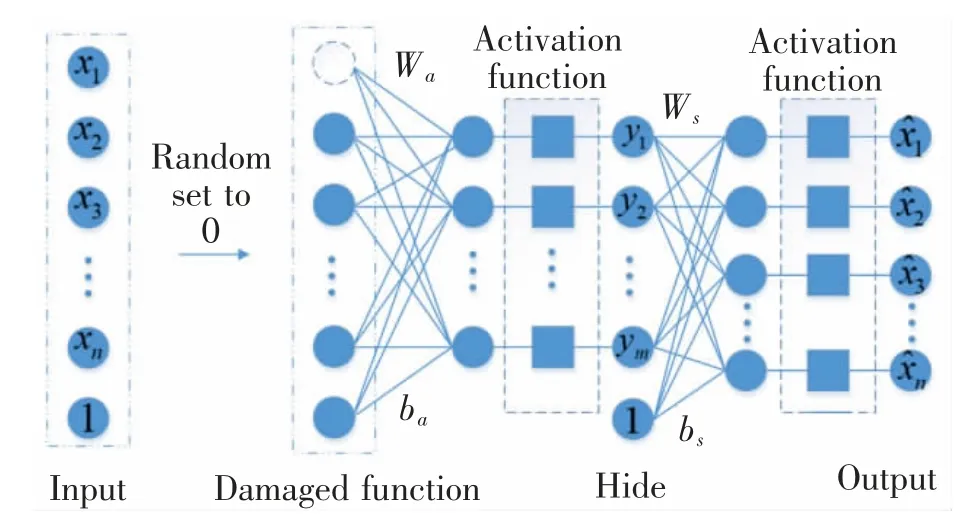
图2 DAE 网络结构图Fig.2 DAE network
降噪自编码器的计算公式为
式中:hW,b(·)为输入数据的重构函数。
对于含有多个样本的样本集,为了使输出逼近原始数据,DAE 的目标函数一般表示为
此外,为避免网络训练过拟合,提高网络的泛化性,还可对DAE 的学习参数设置正则化约束项[18],如使用L2正则化约束,则目标函数可改写为
式中:θ={W,b};W 为两连接层间的权重;b 为各层的偏置;λ 则用于度量数据重构程度和正则化约束之间的权重。
通过上述改进后,DAE 在AE 的基础上,不仅可以对数据进行有效的降维,还能在一定程度上解决原始数据存在噪声的问题,从而对数据进行降噪和降维的双重处理。
针对降噪自编器在滚动轴承故障诊断上的改进与应用中,Meng 等[19]将权重衰减中的L2范数惩罚改为弹性惩罚,以改善参数的稀疏性,通过进行滚动轴承的故障诊断试验发现,该方法相较传统的自编码器更具优越性。Tong 等[20]采用多尺度分析方法从滚动轴承的原始振动信号中提取多尺度特征,再使用稀疏惩罚项和压缩惩罚项对自编码器的损失函数进行正则化,在具体实验中可以有效地区分不同工况下滚动轴承的故障类型和严重程度,提高了DAE 在复杂工况下的性能。Liu 等[21]提出了一种基于非线性预测降噪自编码器进行滚动轴承故障诊断,实验证明该方法鲁棒性强,准确度高,但由于存在监督学习过程,该方法不能很好地识别新的故障类型,也不能很好地识别具有更严重裂纹的同一故障类型。宋威等[22]首先对一维振动信号进行图像灰度化处理,对降噪自编码器的特征提取网络进行改进,即自编码器网络由4 层卷积神经网络和两层全连接神经网络构成,在每个卷积层后均添置归一化层,提升神经网络的训练速度。
1.3 稀疏自编码器
SAE 在自编码器的基础上,通过在隐含层中加入稀疏限制项进行了改进,这种限制会使得隐含层中的节点被抑制激活,而被抑制的节点数量则会因所选取的激活函数发生改变,从而达到增强所提取特征的稀疏性效果,SAE 网络结构图如图3 所示。
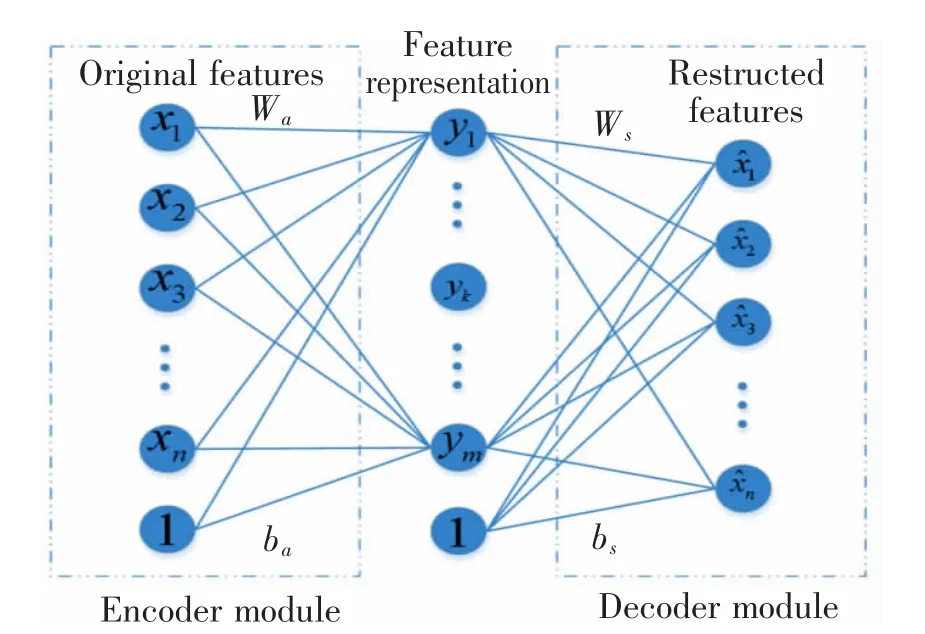
图3 SAE 网络结构图Fig.3 SAE network
在SAE 的各类应用中,常用的稀疏性限制采用L1范数或KL 散度等正则化项。以这两种稀疏性限制为例,当采用L1范数作为正则化项时,SAE 的损失函数可表示为
式中:aj(xi)表示隐含层节点j 对输入xi的激活值;λ表示控制惩罚程度的L1正则化系数。
当采用KL 散度正则化项时,SAE 的损失函数可表示为
相较于基础的自编码器,SAE 能够更有效地学习主要特征,通过降低对次要特征的需求来使提取的特征更具稀疏性。然而,SAE 需要通过参数影响实验来判断该节点是否被抑制,无法直接对某个特定节点进行抑制行为。所以,合理利用SAE 中的稀疏准则、DAE 的降噪机理以及AE 的信号重构能力,将各类自编码器的功能进行点对点的设计有助于挖掘输入的基本信息,提高故障模式分类的鲁棒性。
Dai 等[23]为了挖掘滚动轴承的代表性故障特征,提出了一种结合SAE 和DAE 的叠层稀疏降噪自编码器诊断模型,实验证明该方法诊断准确率、重构误差和迭代时间方面都具有优势,不过该方法非常依赖于数据的驱动。Sun 等[24]建立了一种基于堆叠稀疏自编码器的深层神经网络来挖掘数据间的连接关系,结果显示该方法能够自适应地学习到滚动轴承振动信号的复杂关系,所重构的数据适用于各种故障类别。Jia 等[25]提出了一种基于归一化稀疏自编码器的本地连接网络,来实现自编码器的自动化特征提取功能,结果表明该方法所提取的特征在齿轮箱和滚动轴承的故障诊断上都具有优越性。汤芳等[26]提出了一种基于稀疏自编码的深度神经网络来实现无监督学习自动提取特征的功能,结果表明使用该网络所提取的特征进行故障诊断后能更准确地识别滚动轴承故障类型。袁宪锋等[27]利用堆栈稀疏自编码器实现了滚轴轴承故障信号频域深层特征的自适应学习,通过将降维后的特征可视化可以观察到不同故障类型特征向量之间的重叠程度被降低,分类模型对不同滚动轴承故障类型的判断更准确。
1.4 堆栈降噪自编码器
SDAE 网络是由多个DAE 堆栈组成的深度神经网络,因此其结构也与DAE 有很多相似,其主要目的也是将数据进行压缩重构,然后将重构特征输入到后续的分类模型或回归模型中,SDAE 也存在一定的降噪特性,从而提高预测模型的准确度和鲁棒性[28-29]。SDAE 的网络结构如图4 所示。
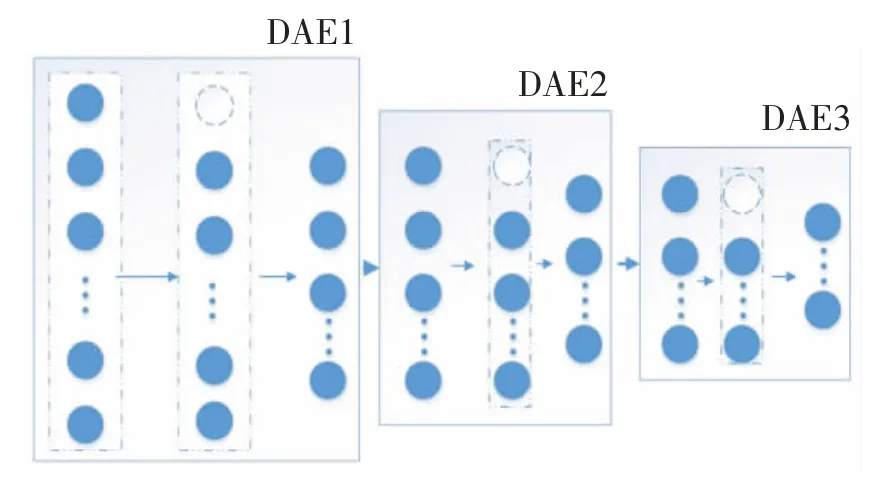
图4 SDAE 网络结构图Fig.4 SDAE network
如图4 所示,SDAE 网络需进行逐层训练和微调才能被训练成更加符合目标函数的网络,即遵循“逐层训练”的原则才能训练得到一个完整的符合目标期待值的SDAE 网络。需要注意的是,在训练某一层超参数时,其他各层超参数需为固定值,并且逐层训练后的网络也需利用样本数据和标签对整个网络进行有监督的微调,该过程可表示为
式中:α 为学习速率,Wij为连接层间权重;bi为第i 层的偏置;l 表示层数;L(W,b;x)为上节所述目标函数。当目标函数达到一定阈值时则表示整体网络已训练完成,训练后的SDAE 网络模型不仅学习了数据之间分布关系,还保留了数据之间的时间相关性特征,从而可以提高数据的优越性,增加分类模型的准确识别率。
Yang 等[30]融合了多变量多尺度样本熵和SDAE,通过引入具有不同分布中心的高斯噪声,实验证明该模型具备良好的去噪能力,此外,对于轴承的故障诊断还具备较高的识别率和较强的鲁棒性。余萍等[31]利用新设计的人工变性天牛算法对SDAE 网络的超参数进行自适应选取从而训练出最优的网络模型,提取滚动轴承更深层次的故障特征,与传统方法相比,该方法具有更好的网络泛化能力、更高的诊断精度和更好的分类性能。杜先君等[32]利用学生心理优化算法对SDAE 网络的超参数进行优化,结果表明优化后的网络模型有效的提升了对滚动轴承进行故障诊断的诊断正确率与诊断速度,但无法有效解决数据缺失、数据类别不均衡、数据分布不均匀等问题。
1.5 其他改进的编码器
除上述几种常用于滚动轴承故障诊断中的自编码器类型外,还有许多关于其他基于自编码器的改进模型在实际故障诊断中的应用。
Shi 等[33]提出了一种基于滑动窗口叠加降噪自编码器的模型来描述具有时间相关特征的数据分布,通过对滚动轴承进行故障诊断实验,验证了所提模型在诊断初始故障类型中具有显著的优越性。Shao 等[34]提出了一种基于集成深度自编码器的网络来解决对于自动特征提取的有效性低的问题,实验证明该网络用于滚动轴承故障诊断方面可以有效地提高准确率,然而,这些新函数的输出有时会不稳定。Li 等[35]将SAE、DAE 和线性解码器分别构造多个深度自编码器来进行滚动轴承故障特征的自适应提取,该方法比单个深度模型和其他集成学习方法更有效,但训练过程耗时久,对实验训练环境要求高。石怀涛等[36]提出了一种基于滑动窗堆栈降噪自编码器和长短时记忆网络的贝叶斯优化的早期故障预测模型来优化针对于滚动轴承的特征提取,从而实现对滚动轴承的早期故障诊断。Yan 等[37]将变分自编码器(variational auto-encoder,VAE)和DAE 相结合来提取具有鲁棒性和判别性的潜在故障特征,实验表明所提模型能对不同的滚动轴承健康状态实现较高的识别精度。张西宁等[38]提出了一种深度卷积自编码网络,通过将卷积网络与自编码器相结合来实现滚动轴承故障复杂特征提取,实验证明该方法能取得更好的故障识别效果,还解决了卷积神经网络权值只能随机初始化的问题。陈志刚等[39]提出了一种改进的深层自编码器集成方法,实现了滚动轴承振动信号的特征自动提取和故障类型自动识别的功能。Shen 等[40]提出了一种基于收缩自编码器的滚动轴承故障诊断方法来获得信号的隐藏的鲁棒特征,从而使诊断模型可以得到更高的准确率。Zhang 等[41]在噪声环境下使用集成深度收缩自编码器进行机械故障诊断,利用集成深度收缩自编码器能自动从输入信号中提取更具代表性和鉴别能力的高层特征的特点来获得更好的故障诊断结果。此外,关于自编码器改进算法及其应用近年来还有很多研究[42-51],表1 归纳了一些自编码器改进算法的优点及改进方式。表1 中相关缩写如下:regularized auto-encoder(RAE),deep convolutional auto-encoder(DCAE),adaptive sparse contractive auto-encoder(ASCAE),hybrid ensemble auto-encoder(HEAE),wasserstein autoencoder(WAE),convolutional auto-encoder(CAE),full convolutional denoising auto-encoder(FCDAE),multi-scale convolutional auto-encoder(MSCAE)。
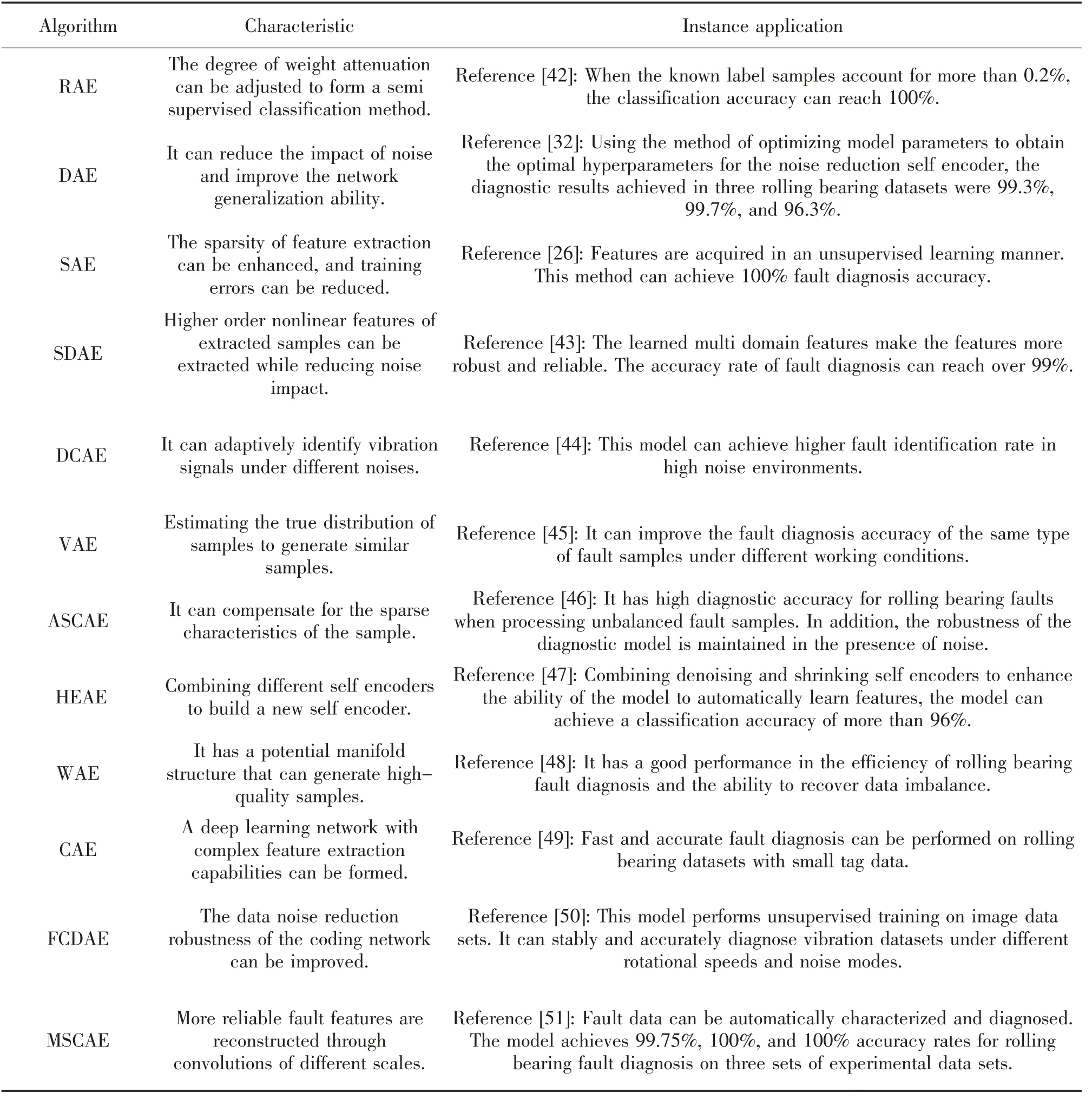
表1 自编码器各改进算法的分析与比较Tab.1 Analysis and comparison of improved self encoder algorithms
2 存在的问题及解决思路
随着现代技术信息化和自动化的发展,对故障诊断算法的需求和要求也愈加高,而基于自编码器的故障诊断技术具有很强的表示学习能力,所以在大数据环境下变得更加自动化和高效。但是,数据样本存在的特征维数高有效信息却有限、传感器的观测值有缺失、数据类别不均衡、数据分布不均匀等问题,造成了特征提取和故障诊断的不确定特性,也限制了自编码器的表示学习能力。因此,基于自编码器的改进及应用仍有很大的研究空间,其理论依据有待完善[52]。
1)故障特征提取的限制。目前,利用自编码器对滚动轴承进行故障诊断应用在已知故障类型下判断故障种类。因此,在半监督或有监督条件下如何使自编码器更具适应性的进行特征提取仍是一个问题,例如稀疏自编码由于在隐藏层中增加了稀疏性限制,其对于随机数据的压缩学习较为困难,而一些堆栈式自编码器虽然具有强大的非线性拟合能力,但处理数据的时间却很长。因此,可考虑重构输入样本及其标签,使自编码器在训练过程中考虑标签损失,或在损失函数中添加带有隐藏标签的正则化项,从而提升特征提取能力。
2)难以适应小样本条件以及数据不充分、不平衡问题。自编码器及其深度结构由于模型结构复杂,在样本数据不充分不平衡和小样本情况下,会产生过拟合现象,例如稀疏降噪自编码器在对数据进行降噪处理时就没有考虑输入与输出间的局部相似性,而卷积稀疏自编码虽然可在短时间内获得最有效特征,但却需要大量的样本进行训练与测试,如何克服样本问题仍是自编码器的一个研究热点。在小样本条件下,可考虑以数据增强为一个解决方法,利用流信息、迁移学习、生成式对抗网络等方法解决该条件下模型的整体设计问题。在数据不充分、不平衡条件下,可考虑以对数据进行预处理为思路,采用欠采样和过采样的方法,或利用代价敏感学习、不平衡学习等模型来解决数据问题。此外,随着宽度学习的发展与应用,还可以考虑将自编码器与宽度学习相结合,使自编码器的结构由深度发展改为宽度发展,达到速度与准确度的双重提高。
3)缺乏有效超参数设置方法。由于基于自编码器的学习模型具有隐含层层数、节点数、权值、偏置等超参数,因此模型的特征提取能力、训练速度、诊断精确度等具有不稳定性[53]。如边缘降噪自编码的噪声强度参数就严重影响其降噪能力与实验成本,特别是一些堆栈形式的改进自编码器和其他深度学习模型相结合的自编码器,由于具有更多的层数与超参数,其模型效果更容易受到影响。超参数数量较少且范围小时,可通过调试实验人工选出最优的超参数设置,但在其他复杂情况时,就应当使用一些优化算法来优化模型中的超参数(如遗传算法、模拟退火算法、学生心理优化算法、灰狼算法等),从而寻找出能够满足最优目标函数的自编码器模型。如何寻找出一个准确率高、适应性强的优化后的自编码器模型仍是一个值得研究的问题。
4)噪声对于网络初始化的影响。信号的有效特性往往淹没在工业背景噪声中,这会导致自编码器对信号的重构能力、降噪能力等性能下降。在自编码器的网络初始化中,噪声的产生是一个不可忽略的问题,绝大多数自编码器及其改进算法对网络参数均采用随机初始化,而诊断模型的训练速度、诊断精确度等也受其影响[54]。L21范数自编码器通过在损失函数中增添正则化项来降低这个影响,又存在处理时间较长这一问题。因此,可考虑在损失函数上引入正则化项来降低网络初始化产生的噪声影响,还可以从网络初始化的角度出发来优化网络降低噪声影响,提高自编码器训练的稳定性,从而提升诊断模型的准确性。
3 结束语
深度学习作为机器学习领域的突破,受到了各个领域的广泛关注,且在滚动轴承故障诊断中的应用也日益增多,自编码器作为一种无监督的深度学习的网络模型,在数据降噪和数据可视化降维方面具有明显的优势。本文介绍了AE 及其一些改进算法的网络结构及其理论理解,梳理了相关算法的创新点与实现方式,最后,通过分析当前仍存在的问题,提供了一些解决问题的思路。
