基于烈度分布的震后城市路网结构韧性分析
2023-06-21谢菲,赵星,申珂
谢 菲,赵 星,申 珂
(河海大学土木与交通学院,江苏 南京 210098)
通过对城市路网韧性的评估分析,有助于识别网络结构中的薄弱环节,在地震发生前采取预防加强措施,提高网络应对灾害的能力,同时在灾后也能提供恢复方向。
地震韧性研究开始于Bruneau 等,总结出韧性的“4R”特性,即鲁棒性、冗余性、资源策略性以及快速恢复性[1]。鲁棒性与冗余性在路网应对灾害发生时的阶段里分别体现出路网抵抗灾害的能力以及部分道路中断后其他路径资源的可替代程度,而资源策略性与快速恢复性则是在灾后恢复阶段中体现出路网迅速恢复至正常状态的能力[2]。由于韧性本身的复杂性,国内外研究中评估方法多样化。Zhang 等[3]基于对网络连通性的分析,构建了一个综合韧性指标WIPW,该评估框架系统性地集成了网络拓扑属性、冗余性、交通救援需求、桥梁结构可靠性等因素,并通过对假想桥梁网络的研究,在灾前阶段采取加固关键桥梁与新建桥梁两项措施降低地震灾害损失,提高网络韧性。王明振等[4]同样将独立路径作为路网抗震韧性的关键,引入节点和路径重要度为权重对可靠独立路径的计算作了改进,研究重庆市渝北区主干路网在不同地震烈度下的网络韧性,地震烈度越大,网络韧性下降幅度越明显。不同于将多个评估标准整合到一个综合度量指标中,部分学者在韧性评估体系中采用一组不同方面的度量指标。Aydin 等[5]构建了随机失效、基于网络密度失效、基于社区结构失效3 种场景来模拟地震事件造成的道路中断情况,并选择介数中心性、最大连通子图、网络效率3 个指标评估韧性,得到影响韧性空间分布最大的关键节点。Wei 等[6]以汶川地震灾区公路网为典型案例,分别从网络密度、最大连通子图、网络效率来讨论全周期路网韧性。除了从网络拓扑层面的视角开展分析,Bocchini 等[7]还基于交通流评价网络韧性,通过判断桥梁震后破坏程度,借助交通分配原理,由通行时间和距离来量化韧性指标。Sanderson 等[8]以太平洋沿岸地区路网为研究对象,综合地震与海啸多重灾害背景,借助道路桥梁易损性曲线分析路网破坏状态,并基于行程时间构建评估指标,分析不同空间尺度下的路网韧性。
目前针对城市内部交通网络抗震韧性评估的研究有限,现有研究中多单一考虑桥梁结构震后破坏的影响,但交通网络中其他组件之间的相互影响同样不能忽视。在对地震灾害造成的道路中断场景进行模拟时,还应考虑地震空间分布特性。鉴于此,本文利用现有的震害预测模型,综合分析道路、桥梁、隧道、沿街建筑产生的震害影响,结合地震烈度衰减分布模型分析震后路段连通性,识别脆弱路段,并以此为基础提出抗震韧性多指标评估方法,研究可为城市路网韧性提升提供参考。
1 基于烈度分布的道路设施震害连通概率模型
1.1 地震下道路连通性影响因素分析
1.1.1 道路单元
道路是交通网络里的主体部分,其破坏程度不仅受所处地震烈度大小的影响,也与自身结构特点有关。根据在道路震害预测基础上确定的7 种震害因子,采用平均震害指数方法[9]来评估道路本身的破坏情况。首先,根据道路震害因子量化值计算平均震害指数,计算公式为
式中:ri为第i 条路段的平均震害指数;Xij为第i 条路段的第j 个震害因子所对应的量化值,各震害因子分类及其量化值如表1 所示。
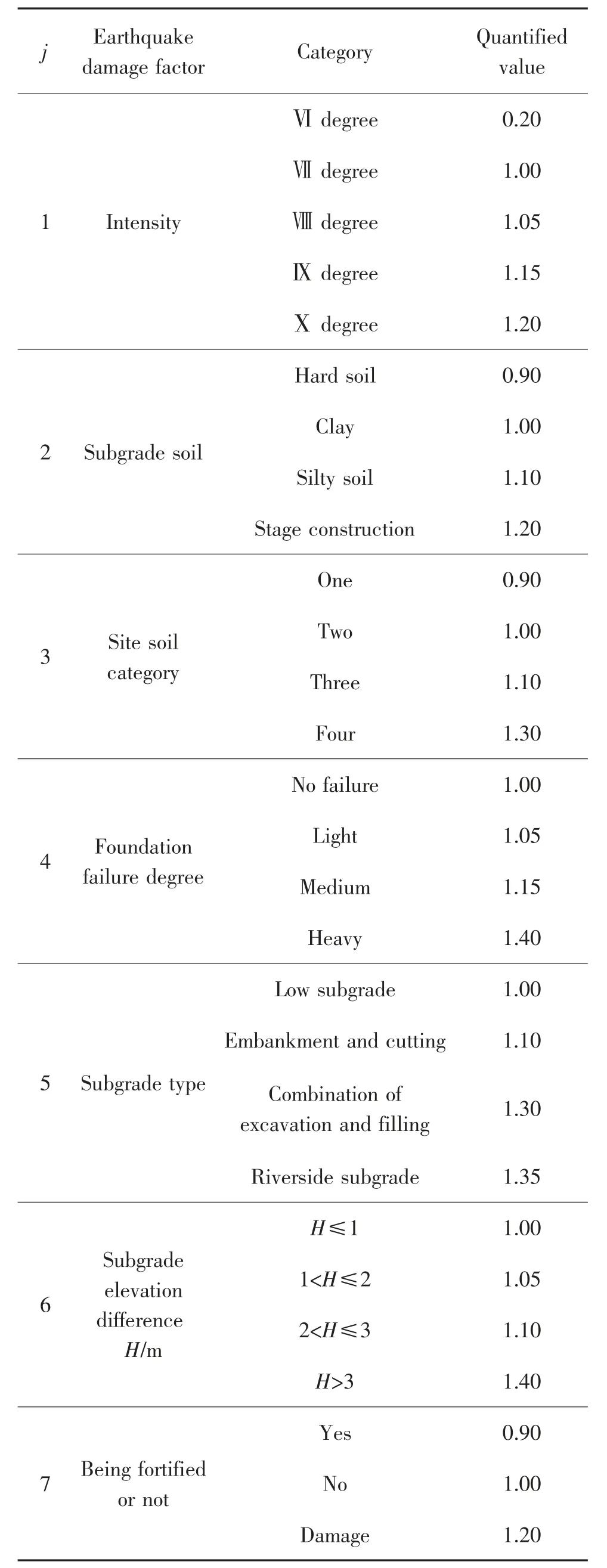
表1 道路震害因子量化值Tab.1 Quantified value of road earthquake damage factor
进而分析道路完好程度,两者之间存在指数关系,道路完好程度系数计算式[10]为
式中:Pr为道路完好程度系数;ri为第i 条路的平均震害指数;r0为路段最小平均震害指数,通常取0.1;σ 为震害离散系数,与地震烈度有关,其推荐值如表2 所示。
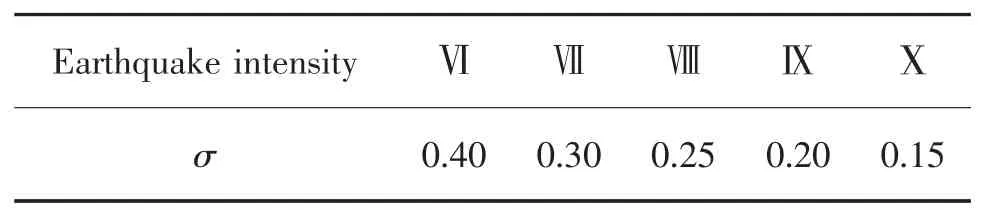
表2 各地震烈度下σ 推荐值Tab.2 Recommended value of σ for each seismic intensity
不同破坏等级下对路段连通性影响不同,通过道路完好程度系数表征路段连通概率,对应关系见表3。
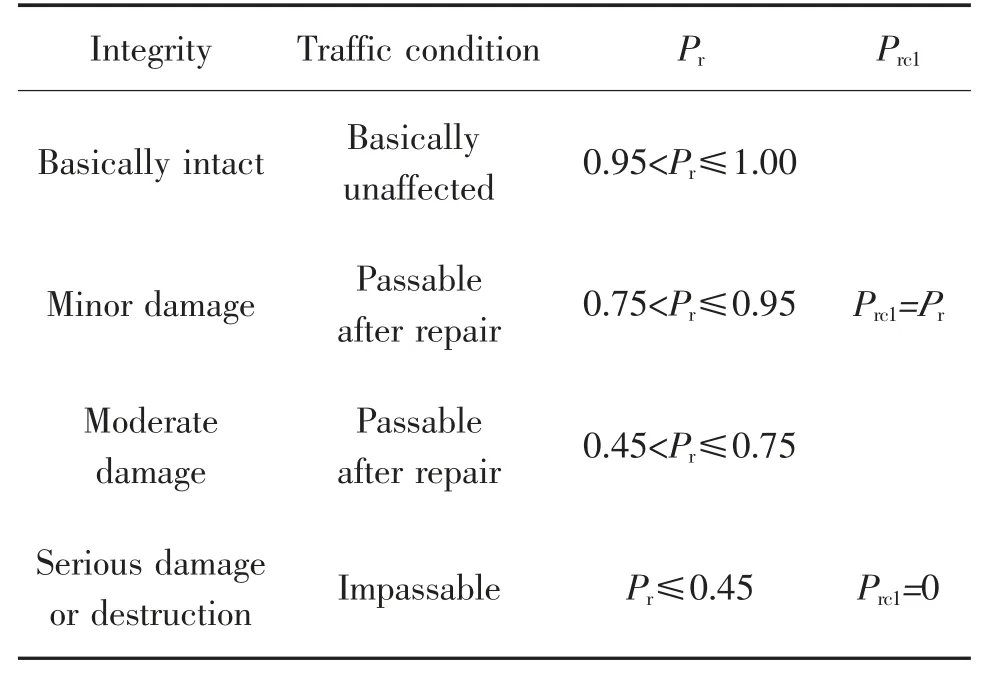
表3 道路完好程度与路段连通概率Tab.3 Road integrity degree and probability of sectionconnectivity
大量经验表明,对于城市内部道路网络来说,道路结构条件相比于城市外部连接道路的情况要更好,所以道路自身结构破坏通常非首要因素,还应考虑沿街建筑物倒塌所造成的瓦砾阻塞。为了分析沿街建筑倒塌产生的瓦砾堆积问题对路段连通性的影响,首先预测其倒塌概率,第j 栋建筑物的倒塌概率计算公式[11]为
式中:IPGV取值由地震烈度决定,其对应关系如表4所示;λ 和ξ 分别是lnX 的平均值和标准方差,其取值见表5。
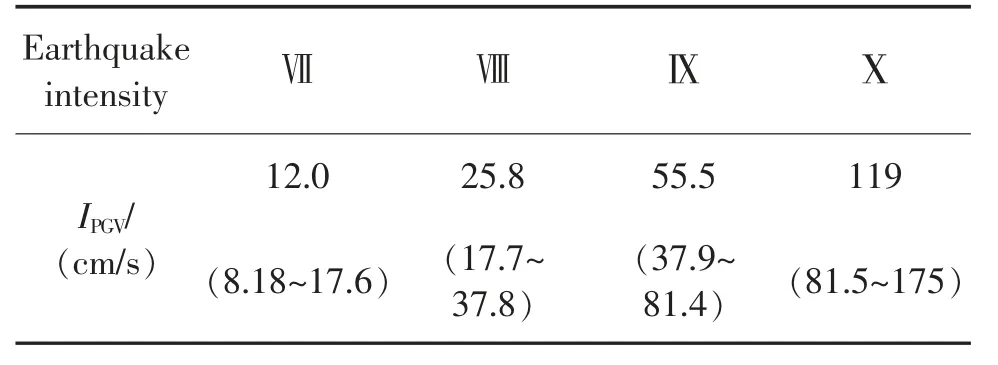
表4 地震烈度与IPGV 的对应关系Tab.4 Correspondence between seismic intensity and IPGV
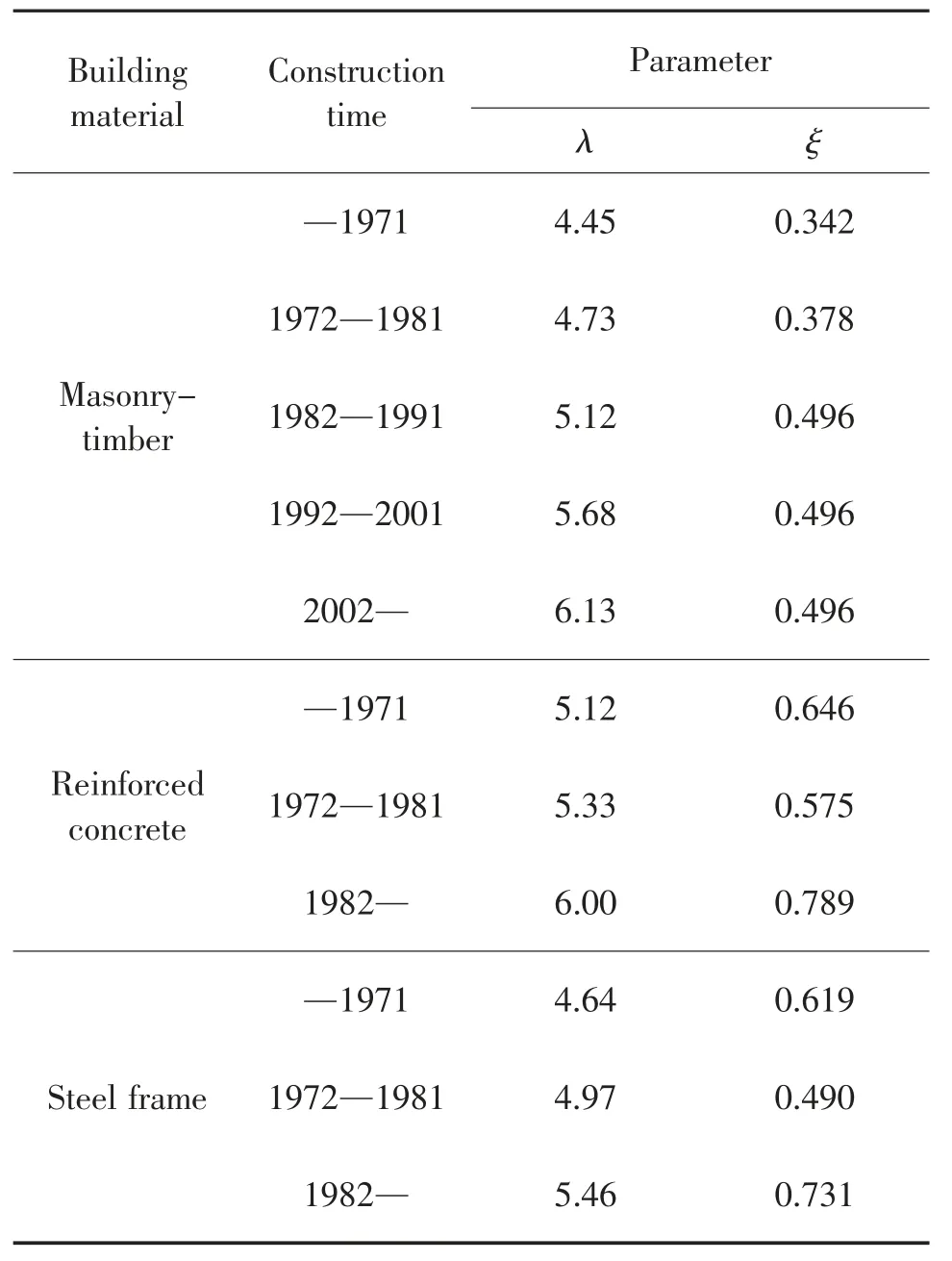
表5 建筑物倒塌概率估算参数Tab.5 Estimating parameters of building collapse probability
建筑物因所处断层位置而表现出倾倒优势方向性,即在地震中,同一断层范围内的建筑倒塌方向有一定的规律性[12]。因此,在传统建筑物倒塌瓦砾阻塞量模型中作出改进
式中:wjr为第j 栋建筑物前道路富裕宽度;wd为建筑物退后距离;ws为人行道宽度;Bj为第j 栋建筑物产生的瓦砾阻塞量;δj为第j 栋建筑物倒塌影响宽度系数,文献[13]中对地震作用下建筑结构竖向倒塌影响开展研究,给出其取值见表6;Hj为建筑物高度;αj表示建筑物j 倾倒的方向角度;Aj为层面积;Pj,PGV为第j 栋建筑物的倒塌概率;n 为该路段沿街的建筑总栋数。
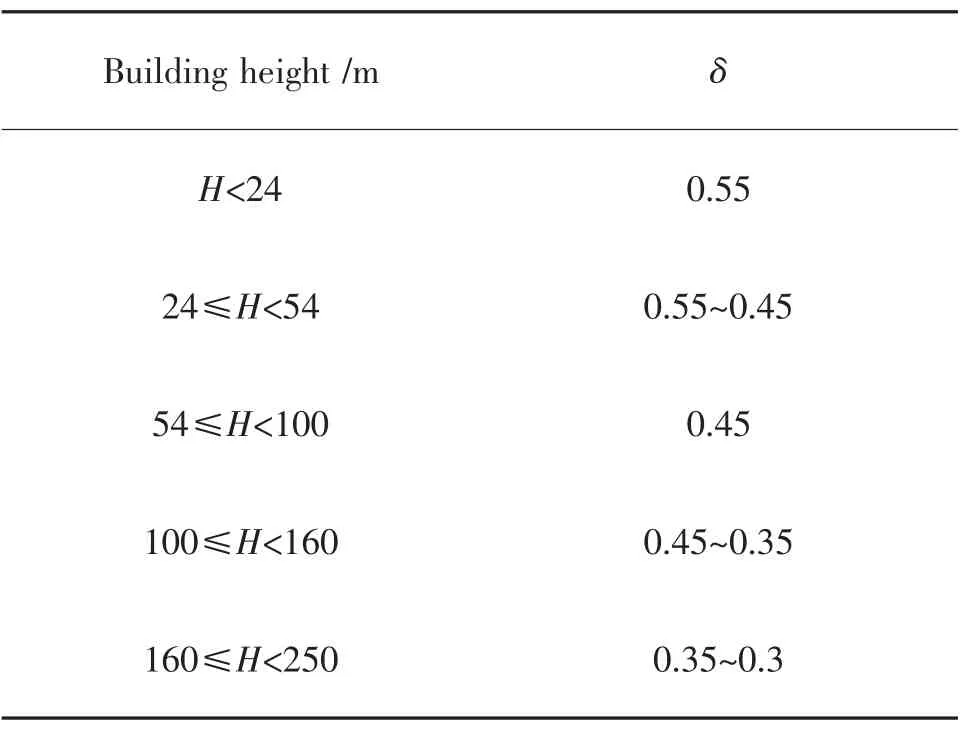
表6 建筑倒塌破坏影响范围系数Tab.6 Coefficient of influence area of building collapse
最后,通过对路段瓦砾阻塞量密度与其临界值的计算比较,可得到在建筑物倒塌影响之下的道路单元连通概率,相关公式如下
式中:Q 为瓦砾阻塞量密度,m2/m2;T 为沿街瓦砾总阻塞量,m2;L 为路段长度,m;W 为路段有效宽度,m,其值为2(wd+ws)+w0,w0为行车道宽度;Qc为临界瓦砾阻塞量密度;Bc为临界沿街瓦砾阻塞量;Lc为标准路长;Wc为路段标准有效宽度。
1.1.2 桥梁单元
桥梁由于其在网络中所处位置的特殊性,一旦遭受地震的破坏,对路网整体的连通性会产生不利影响,若损坏严重会导致短时间内修复较为困难。对桥梁的震害分析首先应研究桥梁的震害度A[10],预测式为
式中:c0为调整系数,一般可以取0.98;a 为影响桥梁的9 类震害因子;b 为震害因子的类别;cab为第a类震害因子中所对应的第b 个类别因素的系数,各因素的系数值如表7 所示。然后引入桥梁震害指数K,结合震害度研究桥梁的震后连通概率,对应关系见表8。
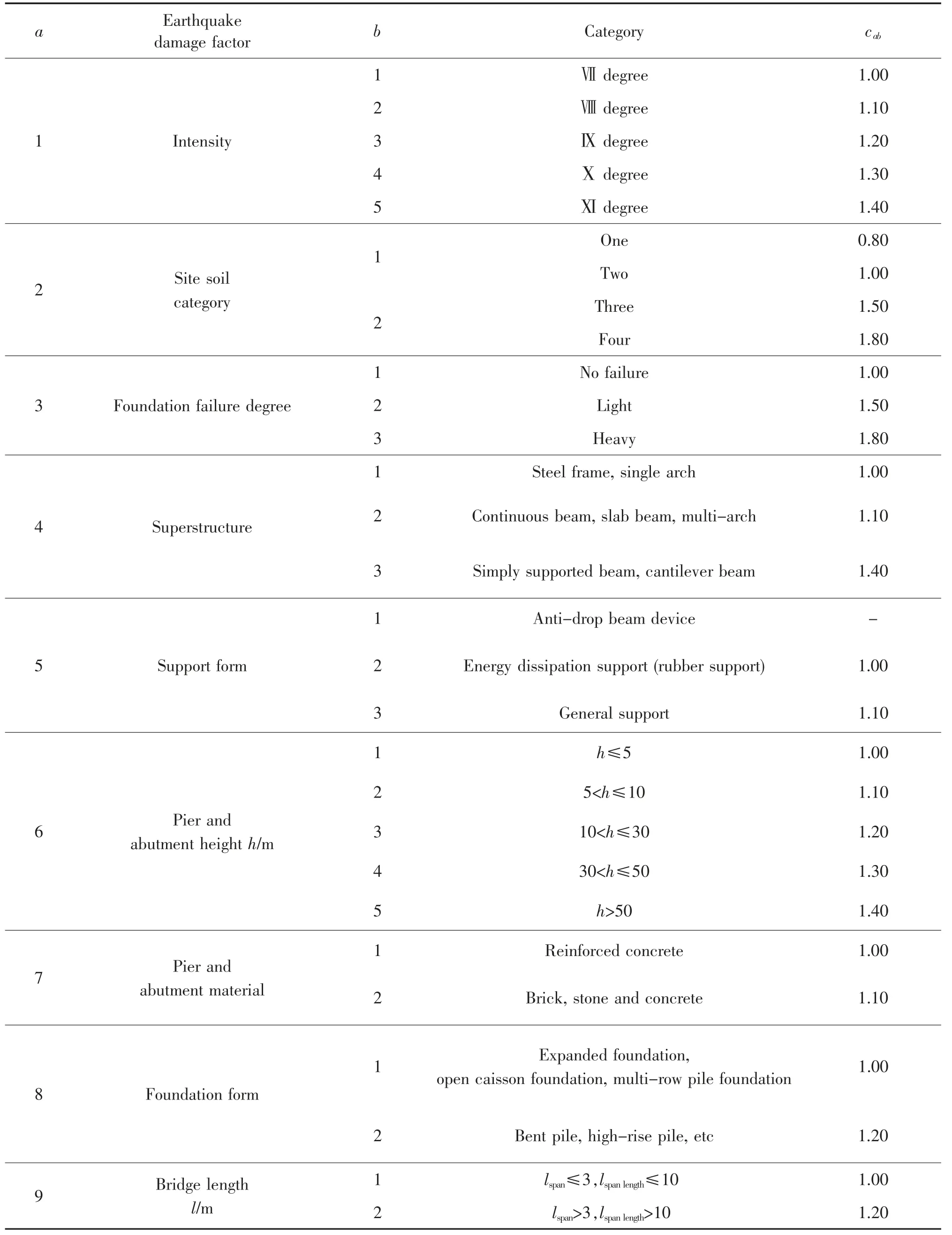
表7 桥梁震害度影响系数Tab.7 Influence coefficient of bridge earthquake damage

表8 桥梁震害程度与连通概率Tab.8 Earthquake damage degree and probability of bridge connectivity
1.1.3 隧道单元
隧道通常具有良好的抗震性能,但当隧道的结构不足以抵抗强地震作用时,可能会出现裂缝、垮塌等现象,导致交通网络异常。评估隧道的震害指数计算式[14]为
式中:B 为隧道震害指数;j 为影响隧道的7 类震害因子;k 为震害因子的类别;bjk为第j 类震害因子中所对应的第k 个类别因素的系数,系数如表9所示。
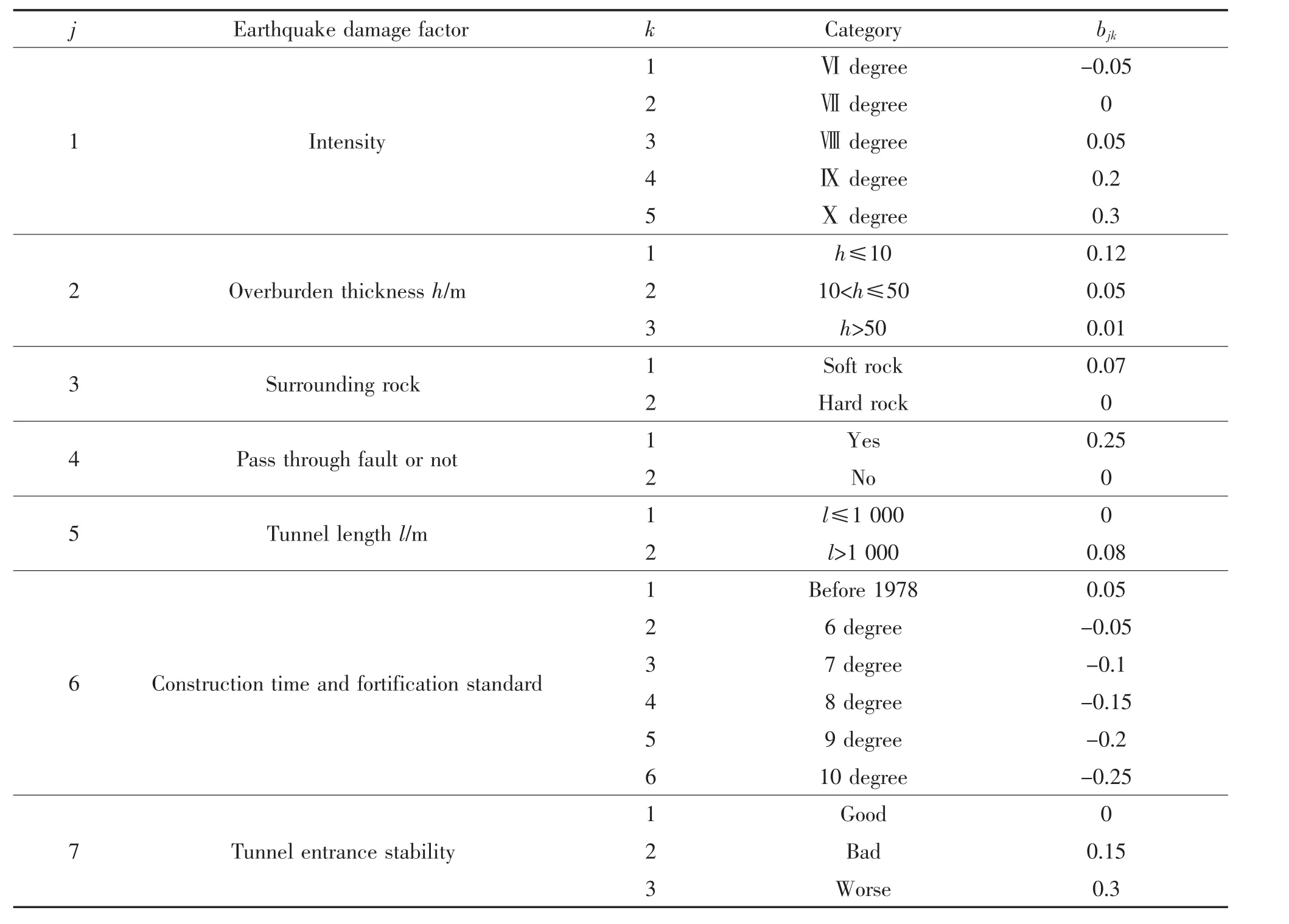
表9 隧道震害因子系数Tab.9 Coefficient of tunnel earthquake damage factor
根据计算所得的隧道震害指数,进一步确定隧道连通概率,对应关系见表10。
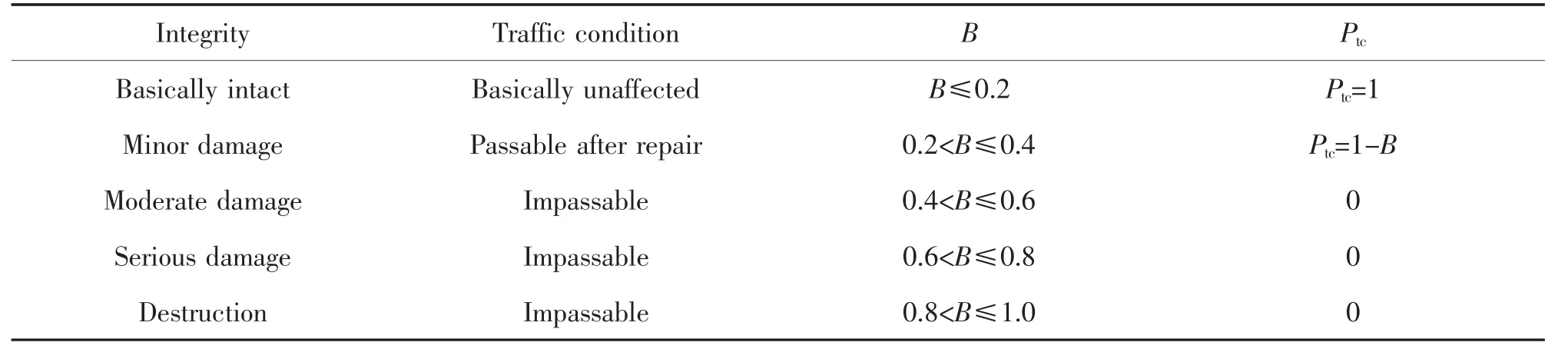
表10 隧道连通概率Tab.10 Probability of tunnel connectivity
1.2 地震烈度衰减分布
地震的产生往往具有不确定性,其主要的三大特征参数分别是震源位置、地震震级、地震烈度。震源位置是指发生地震的中心,地震震级是表示地震的强弱程度,地震烈度用以表征地震所带来的破坏程度。在上述对各道路设施的震害分析中离不开对地震烈度的判断。
根据《中国地震动参数区划图》中提出的潜在震源区三级划分方法[15]:第一步,划分地震统计区;第二步,在地震统计区内划分背景源,主要依据地震区内不同区域在构造背景上的差异及对地震活动性的影响;第三步,在背景源内根据局部区域的构造条件来划分构造源,示意图见图1。在潜在震源区的内部,地震发生的概率是相同的。
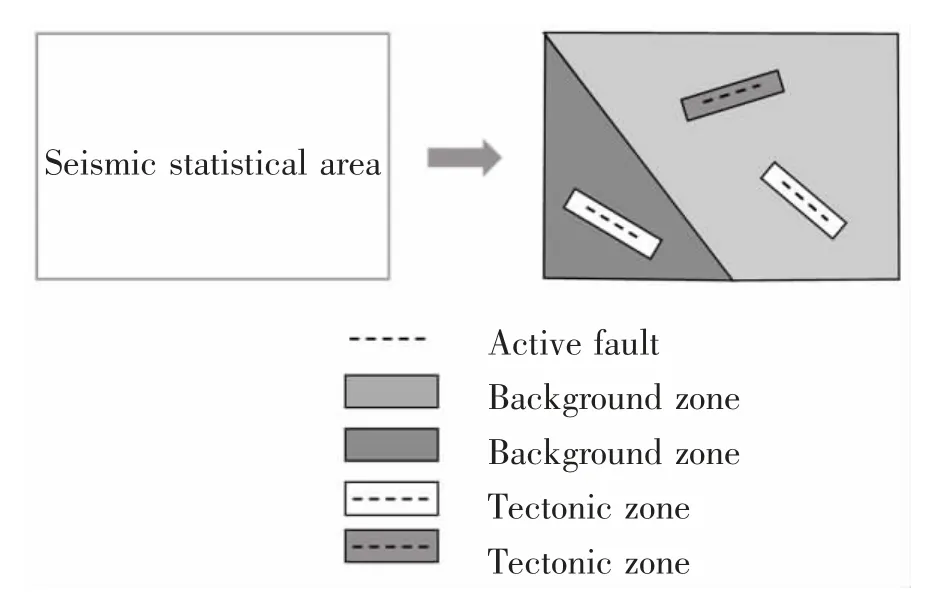
图1 潜在震源区三级划分示意图Fig.1 Schematic diagram of the three-level division of potential epicenter area
当地震烈度不超过Ⅵ度时一般不会对道路基础设施产生较大损坏,本文重点考虑地震烈度为Ⅶ、Ⅷ、Ⅸ度的分布情况。为了表征地震烈度随着震源中心沿各个方向衰减的特性,研究中常采用椭圆衰减模型[16],椭圆两轴上各点的地震烈度由下列公式所得
式中:I 为地震烈度;M 为地震震级;r 为距震中的距离;a、b、c、r0均为回归参数。
根据式(12)计算结果可得到椭圆等震线,每组等震线以震源为中心,具有相同的长轴方向。其中,构造源内长轴方向与此构造源的活动断层走向相同,而背景源内的长轴方向则为距离震中最近的构造源内长轴方向[17]。地震烈度分布示意图如图2 所示。
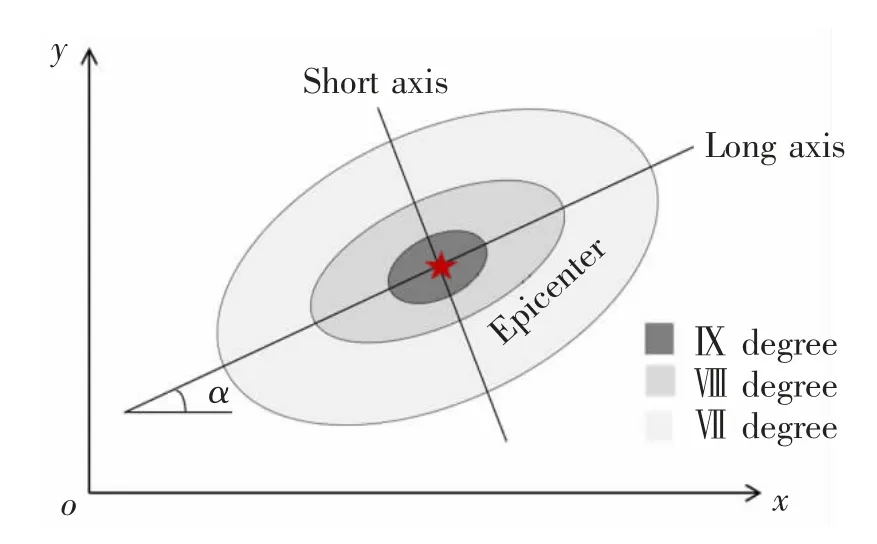
图2 地震烈度分布Fig.2 Distribution of seismic intensity
1.3 路段连通概率
假设道路单元、桥梁单元和隧道单元各自独立,其中某一部分受到地震损害便会对路段通行产生影响,故路段连通概率为
式中:Pc为路段的连通概率;Prc为道路单元连通概率,包括道路本身连通概率Prc1和建筑物倒塌下道路连通概率Prc2;Pbc为桥梁单元连通概率;Ptc为隧道单元连通概率。当路段中不包含某一单元时,则在路段中的连通概率取1 计算。
结合地震烈度衰减分布模型中对路段单元所处烈度区进行判定,若路段整体位于单一烈度区内则直接计算连通概率,但当路段跨越了多个烈度区时,路段不同地方的震害程度可能存在差异。根据烈度分区结果将路段分成N 个元路段,则位于第i个烈度区的元路段占比为
式中:L 为路段总长度;ΔLi为位于第i 个烈度区的元路段长度。
整条路段连通概率近似为
式中:Pc,i为第i 个烈度区路段连通概率。
2 城市道路网络结构抗震韧性多指标评估
尽管在不同研究领域里对韧性内涵的定义存在差异,但达成的主要共识有网络受到扰动后抵抗干扰的能力以及恢复至正常状态的能力。目前对于交通网络结构韧性的研究未形成统一的评估指标,大多通过网络拓扑层面的属性来表征。本文在剖析城市路网遭受地震时受损机理的基础上,重点关注网络结构应对攻击时不同属性的变化情况,分析网络韧性表现。网络拓扑建模是进行韧性评估的基础,实际的城市交通系统可以抽象成由节点和边构成的网络拓扑图,将道路交叉口简化为节点,路段简化为边。
2.1 韧性评估指标
2.1.1 网络效率
网络效率反映交通网络整体的通行效率,网络效率越大,意味着节点对之间运输服务能够快速实现,具有较强的抵抗能力,表示如下
式中:n 为网络节点的总数;dij为节点i 到节点j的最短路径长度,可用Dijkstra 算法实现最短路径搜索。
2.1.2 区域可达性
可达性衡量交通网络通行的便捷程度,通常与行驶时间有关。基于对潜在可达性的研究基础上,引入节点人口权重得出区域可达性用以评估韧性[18],计算公式如下
式中:IPAi为潜在可达性;Pi和Pj分别为节点i 和j的人口数;Tij为节点i 到节点j 间最短路径中各路段通行时间之和;wi为节点人口权重。
2.1.3 平均独立路径数量
不同于上述指标中的最短路径,独立路径是指两节点之间不共用任何一条路段的连通路径集合。独立路径集合的选取方法为:首先找到两节点之间的全部路径与最短路径;然后在全部路径中剔除与最短路径有共用路段的路径,得到路径集合a;最后在路径集合a 中同样由路径最短原则逐个排除相互之间有共用路段的路径,得到两节点间包括最短路径在内的独立路径集合。
当节点对的某条路径受到攻击破坏后,网络中存在其他不受影响的路径保障正常运行,表现出一定的冗余性。对于震后应急期,在恢复资源无法立即就位时,独立路径的存在也尤为重要。表示如下
式中:Nij为节点i 与节点j 之间的独立路径数量;为网络受损后的独立路径数量。
2.2 地震场景下路网韧性评估框架
城市路网抗震韧性评估方法如图3 所示,具体描述如下:
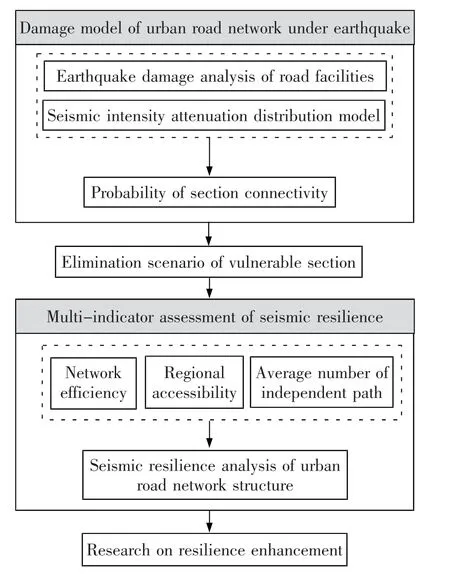
图3 抗震韧性评估框架Fig.3 Seismic resilience assessment framework
步骤1 根据震源位置与地震震级,由地震烈度衰减模型得到地震场景下的烈度分布情况,确定路网各路段所处烈度区;
步骤2 对道路、桥梁、隧道、沿街建筑进行震害分析,计算出基于烈度的路段连通概率,识别脆弱路段;
步骤3 构建震后路段累积失效场景,分别从网络效率、区域可达性、平均独立路径3 种角度的度量指标对网络结构韧性进行分析;
步骤4 基于韧性评估结果,若网络韧性较差则需要进一步提升韧性。
3 算例分析
3.1 算例介绍
本文选取南京市鼓楼区东南角区域主要道路网络作为研究对象,通过对道路网络的统计,将路网划分为21 个节点和31 条路段,其中包括3 条隧道,无桥梁。根据中国地震局地质研究所统计的全国活动断层,将位于该区域的南京-湖熟断层作为构造源,该断层倾角65°。路网拓扑结构与断层位置分布见图4。
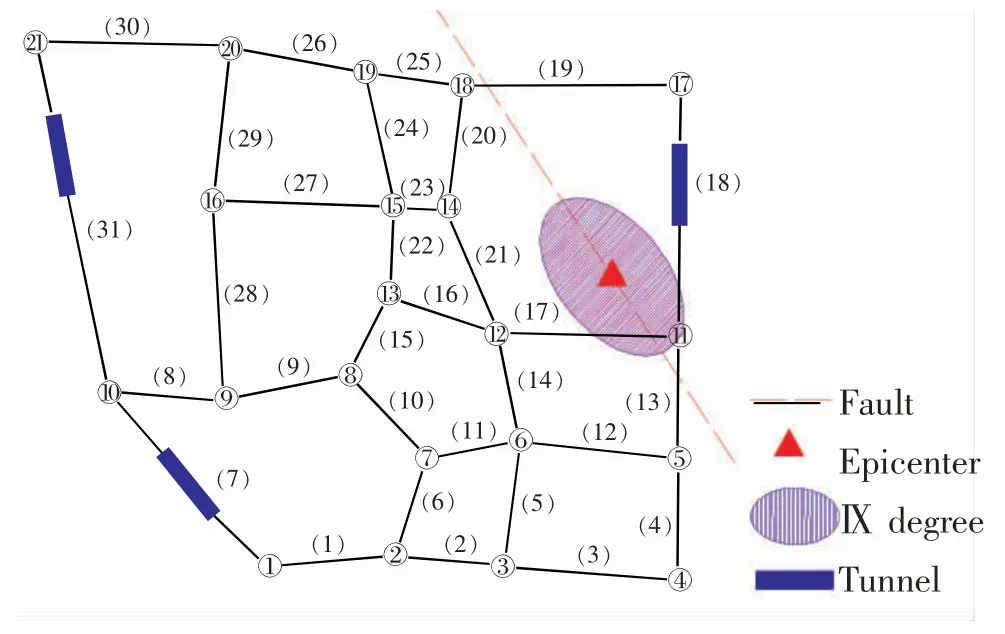
图4 地震烈度分布下的道路网络拓扑简图Fig.4 Road network topology diagram under seismic intensity distribution
在此背景下,假定在图4 中所处位置发生了7级地震,根据烈度衰减分布模型得到烈度分区结果:阴影区域为烈度Ⅸ区,等震线以外区域处于烈度Ⅷ区。根据建筑物倾倒方向与断层的关系,假设在此次地震中,断层西南侧建筑物由北向南倾倒,断层东北侧建筑物由西向东倾倒。
3.2 韧性分析
3.2.1 失效场景
求出各路段在地震下的连通概率。以路段17为例介绍计算过程。路段17 跨越不同烈度区,长度为760 m,根据烈度分区结果可知有2 段元路段,位于烈度Ⅸ区和Ⅷ区的元路段长度分别为387 m 和373 m,得到n1,Ⅸ和n2,Ⅷ分别为0.509 和0.491,则路段17 的连通概率为
式中:Pc17,1,Pc17,2分别为处于烈度Ⅸ区和Ⅷ区的连通概率。
位于单一烈度区的路段连通概率由式(13)直接计算可得。
结合表11 中有关道路可靠性的分析判断,研究路网中有3 条非可靠状态道路,其连通概率与所处位置分别如表12 和图5 所示。
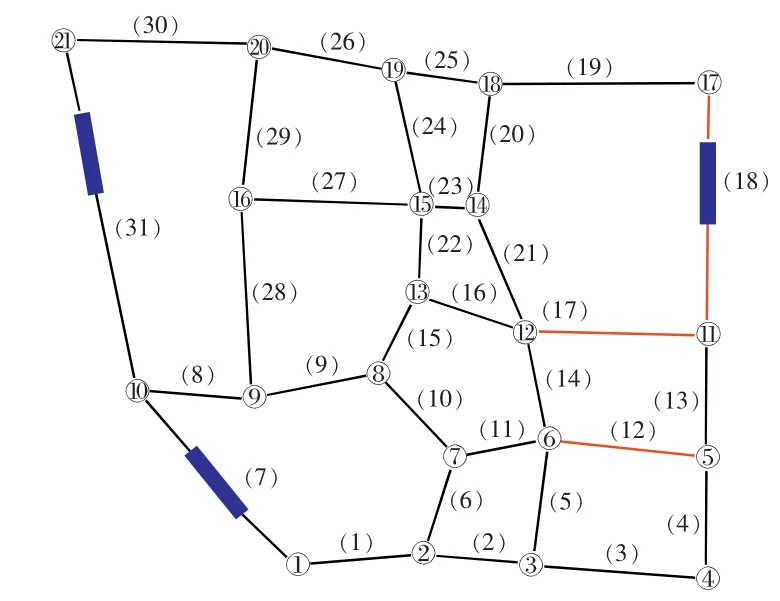
图5 脆弱路段位置示意图Fig.5 Location diagram of vulnerable sections

表11 道路可靠性状态Tab.11 Road reliability state

表12 脆弱路段连通概率Tab.12 Probability of vulnerable section connectivity
研究中选取上述3 条路段来构建累积失效场景,模拟此次地震背景中路网的受影响程度,进而对道路网络结构韧性进行分析。失效场景模拟情况见表13。
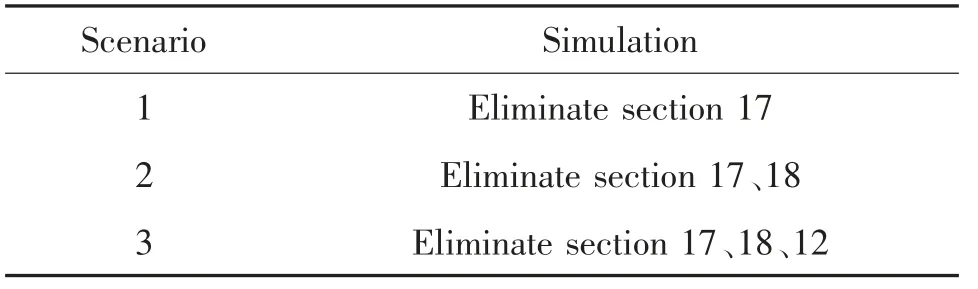
表13 失效场景模拟Tab.13 Elimination scenario simulation
3.2.2 韧性指标分析
从图6 结果可以看出,正常状态下的道路网络韧性随着失效路段的增加而逐渐降低,在路段18和路段12 接连中断后,韧性指标下降程度更为明显。在路段17 失效时,网络韧性稍有下降,此时网络具有一定的鲁棒性。当路段18 参与失效后,平均独立路径数量从正常状态下的1 降为0.898,即使网络中节点对之间仍存在有一定数量的独立路径,但可能会对某些节点的应急救援产生影响,例如节点11 和节点17,可供选择的通行路径较少。当路段12 参与失效后,网络效率下降幅度高于其他路段,研究路网的运输效率受到影响,使得节点间传输信息难度增加、消耗的时间资源更多,同时意味着网络结构的抗干扰能力也因此降低。对于区域可达性,通过比较灾害模拟前后可达性下降变化比率,网络韧性明显下降出现于路段18 和路段12 的失效,两种场景下的下降比率分别是-7.017%和-11.024%,可见节点间可替代的便捷路径也有所减少。
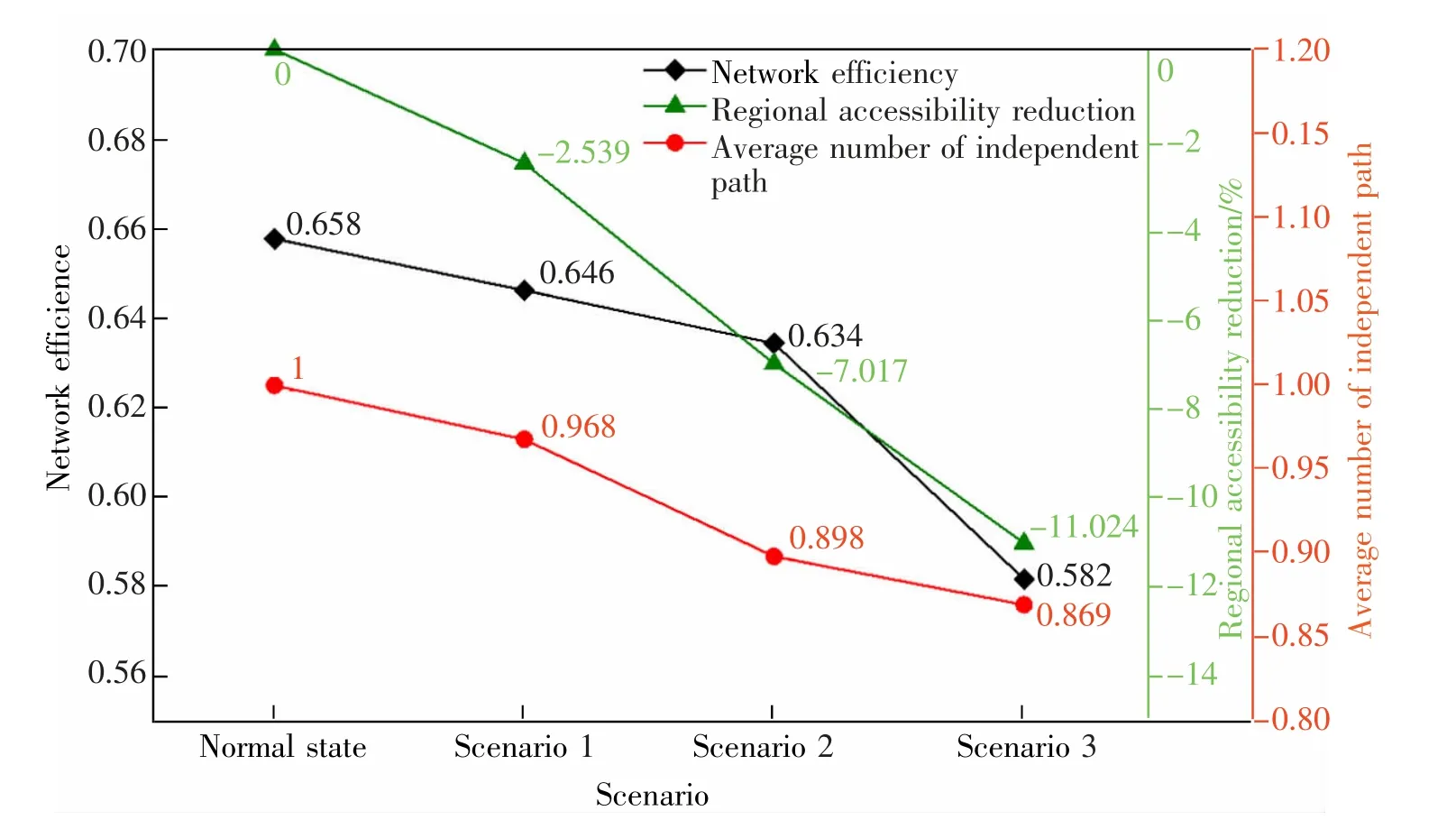
图6 不同场景下的网络韧性Fig.6 Network resilience in different scenarios
通过韧性结果分析,各路段在网络韧性中表现出不同的重要性。路段18 是连接节点11 和节点17的关键路段,中断后不仅直接影响了两个节点间的连通性,也会削弱两个节点与其他节点之间的连接关系。路段12 中断还会增加多个节点的绕行距离。
3.3 韧性提升方向
为了有效提高网络的韧性,通常可以通过改变网络拓扑结构得以实现,例如在关键位置增加路段,然而在现实情况中,已建成的城市内部道路网络由于空间限制而无法达到目的,此时重点应提高道路可靠度,尤其是靠近活动断层区域,定期检查和加固,增强道路网络的鲁棒性去抵抗地震灾害攻击,特别是当关键路段包含桥梁、隧道等设施单元时,通常是路网的薄弱环节,例如路段18,一旦失效会使得多方面韧性下降明显,日常维护便显得非常重要。除了对道路层面的考量,应急资源中心的合理选址,有利于在路网遭受灾害和受损之后,加快路网韧性的恢复。
4 结论
1)针对不同路段累积失效场景下的韧性对比分析,可以得出薄弱且重要的关键路段失效会对多方面网络韧性下降造成明显影响。
2)在韧性提升中若因现实条件限制而无法从网络拓扑结构作出改变,则应重点提高活动断层范围的道路可靠度,以及科学合理地规划应急资源中心。
3)研究不同于随机攻击或完全失效,一定程度上完善了受灾情景模拟真实性的问题,但仅针对路段分析网络韧性变化,未来还可考虑节点联合受攻击的情况。
