数学家的“数学”墓碑（下）

林革

麦克劳林的墓碑

科林·麦克劳林是苏格兰数学家（图13），成就非凡，被誉为18世纪英国最有影响力的数学家之一。

1698年2月，麦克劳林出生于苏格兰的基尔莫登，自幼父母双亡，由叔父抚养成人。他从小便展现出过人的数学天赋。11岁时，麦克劳林考入格拉斯哥大学，研修神学。入校不久，他就对数学产生了浓厚兴趣；于是，在一年后，便转攻数学。17岁时，麦克劳林取得硕士学位，并为自己关于重力做功的论文进行了精彩的公开答辩。

19岁时，他被聘为阿伯丁大学的数学教授，并主持该校马里歇尔学院有关数学学科的工作。两年后，麦克劳林被选为英国皇家学会会员。1722—1726年，他在巴黎从事研究工作。1724年，麦克劳林因物体碰撞的杰出论文而荣获法国科学院资金奖励。回国后，麦克劳林任爱丁堡大学教授。

1719年，年仅21岁的麦克劳林在访问伦敦时见到了牛顿，从此成为牛顿晚年的得意门生。1724年，由于牛顿的全力推荐，麦克劳林继续获得教授席位。

麦克劳林在21岁时发表了第一本重要著作《构造几何》，书中描述了作圆锥曲线的一些新的巧妙方法，精辟地讨论了圆锥曲线及高次平面曲线的种种性质。麦克劳林于1742年撰写的《流数论》以泰勒级数作为基本工具，是第一本对牛顿的流数术给出符合逻辑的、系统解释的著作。他得到數学分析中著名的麦克劳林级数展开式：若函数f（x）在包含0的某个闭区间[a，b]中具有n阶导数，且在开区间（a，b）中具有n+1阶导数，则对闭区间[a，b]中的任意一点，下式成立：

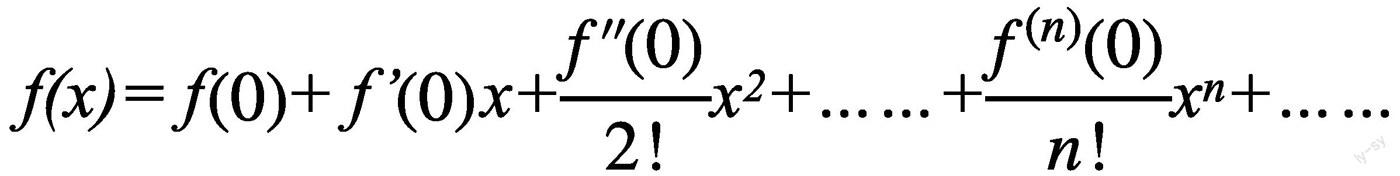
他同时用待定系数法给予证明，这成为高等数学中无论如何也绕不过去的一个公式。由此可见，这位英国数学家非同凡响的创造力和影响力。

此外，麦克劳林在代数学领域也有杰出贡献。在于1748出版的遗著《代数论》中，他创立了用行列式方法求解多个未知数联立线性方程组，后来，由数学家克莱默重新完善，成为现今的克莱默法则。

麦克劳林的成长经历堪称“神童—奇才”般水到渠成。也正是由于牛顿对其研究工作的无私支持和帮助，麦克劳林得以在几何学和应用数学上取得重大成就。因此，他终生感激牛顿对自己的栽培和提携，并致力于继承、捍卫、发展牛顿的学说。他曾打算写一本名为《关于伊萨克·牛顿爵士的发现说明》的书，但未能完成便去世了。麦克劳林的墓碑上刻有“曾蒙牛顿推荐”（图14），以表达对牛顿的感激之情。

高斯的墓碑

高斯是历史上最伟大的数学家之一（图15），被世人称为“数学王子”，其贡献遍及基础数学和应用数学的各个领域，对现代数学的发展产生了深刻影响，其成就足以与阿基米德、牛顿比肩。

有关高斯天纵之才的神奇传说，可以说在全球范围内广为流传。除了妇孺皆知的10岁小高斯巧算1+2+3+4+5+…+99+100的故事，最为数学爱好者耳熟能详的，当数1795年进入哥廷根大学的19岁高斯，一夜之间完成两千年来连阿基米德和牛顿也没能解决的世界级难题：用圆规和一把没有刻度的直尺画出一个正十七边形。尽管高斯日后取得了更大的成就，但他本人对此念念不忘，并在临终前留下遗言：“我死后，什么东西都不想要，只希望在我的墓碑上做一个正十七边形。”

正三角形和正五边形早已为人熟知，而正257边形、正65537边形由于过于复杂，迄今为止尚无人能有所进展。因此，正十七边形自然成为高斯传说中的最佳数学背景。

高斯去世后，哥廷根大学为之建造的墓碑上（图16）并没有什么正十七边形的图案，不过，这并不影响高斯的伟大和非凡。有德国慕尼黑博物馆中的纪念文字为证：“他的思想深入数学、空间、大自然的奥秘，他测量了星星的路径、地球的形状和自然力，他推动了数学的进展，直到下个世纪。”

笛卡尔的墓碑

笛卡尔是著名的法国数学家、物理学家、哲学家（图17），“我思故我在”便是他的名言。他对现代数学的发展做出过重要贡献，因将几何坐标体系公式化，而被认为是“解析几何之父”。

在笛卡尔之前，几何与代数是数学中两个不同的研究领域。笛卡尔站在方法论的高度，认为希腊人的几何学过于依赖于图形，束缚了人的想象力。他觉得当时流行的代数学完全从属于法则和公式，不能成为一门改进智力的科学。因此，他提出，必须把几何与代数的优点结合起来，建立一种“真正的数学”。

1637年，笛卡尔发表了在数学史上具有划时代意义的光辉巨著—《几何学》，标志着解析几何学的诞生。在这本著作中，笛卡尔首先建立了直角坐标系，为利用代数的、解析的方法解决几何问题提供了必要条件；并且，他使数学的两大基本要素“数”与“形”统一起来，用代数方法研究、解决几何问题，也可以运用几何方法解决代数问题，进而从根本上改变了从古希腊开始的代数与几何分离的趋向，推动了数学的发展进程。

笛卡尔的天才创见也为微积分的创立奠定了基础，从而开拓了变量数学的广阔领域。最为可贵的是，笛卡尔用运动的观点，把曲线看成点的运动的轨迹，建立了曲线和方程的对应关系。这种对应关系的建立，不仅标志着函数概念的萌芽，而且表明变数进入了数学，使数学在思想方法上产生了巨大转折—由常量数学进入变量数学，从而引发数学的深刻革命，有效地解决了现实中的许多重大问题，大大促进了生产力和科学技术的发展。

《几何学》中还包括方程理论，其中最著名的是“待定系数法”。后来，待定系数法不仅成为初等数学里解决多项式因式分解、分式的分项分解的有力工具，也是高等数学中计算积分、级数以及求解微分方程的重要方法。此外，人们在笛卡尔的手稿中还发现，他于1639年就已掌握了欧拉在1750年才发表的凸多面体的棱数、面数、顶点数三者之间的数量关系：顶点数-棱数+面数=2，这是图论中的定理。

笛卡尔去世后，他的著作被罗马教廷列为禁书，直到1740年，禁令才被解除。1819年，笛卡尔的骨灰被移入巴黎最古老的教堂—圣日耳曼德佩教堂中，在他的墓碑（图18）上，刻着这样一句话：“笛卡尔，欧洲文艺复兴以来，第一个为人类争取并保证理性权利的人。”

希尔伯特的墓碑

德国数学家希尔伯特是19世纪和20世纪初最伟大、最具影响力的数学家之一（图19）。他领导了著名的哥廷根学派，使哥廷根大学成为当时全球数学研究的重要中心，并培养了一批对现代数学发展做出重大贡献的杰出数学家，因而享有“数学世界的亚历山大”和“数学无冕之王”的美誉。

1880年秋，18岁的希尔伯特进入著名的柯尼斯堡大学专修数学，在此期间，他结识了闵可夫斯基和阿道夫·赫维茨两位德国青年数学家。他们每天下午5点准时到校园的苹果树下会面，日复一日地进行着自由交流、探讨的“数学散步”，这为希尔伯特的未来发展奠定了坚实基础。

1884年，希尔伯特获得博士学位，并留校任教；1893年，他被任命为数学教授。1895年，应数学家克莱因邀请，希尔伯特赴哥廷根大学任教，此后一直在“数学之乡”哥廷根生活和工作。

希尔伯特的数学研究涉及代数不变式、代数数域、几何基础、变分法、积分方程、无穷维空间、物理学和数学基础等，在这些领域中，他都做出了重大的或开创性的贡献。1897年，他的《代数数域的理论》正式发表，立即在數学界引起巨大反响，数学家们称之为19世纪代数数论的顶峰。1899年初，希尔伯特的《几何基础》出版，成为公理化思想的代表作，并由此推动形成了“数学公理化学派”，可以说，希尔伯特是近代形式公理学派的创始人。在横跨两个世纪的60年数学研究生涯中，希尔伯特的研究足迹几乎遍及现代数学的前沿阵地，他的数学思想深深渗透在整个现代数学领域。

值得大书特书的是，1900年，在巴黎召开的第二届国际数学家大会（ICM）上，年仅38岁的希尔伯特发表名为《未来的数学问题》的演讲，提出当时世界上还没有解决但对未来数学发展有重大影响的23个数学问题，史称“希尔伯特问题”，其中涉及现代数学的大部分重要领域，为20世纪的数学研究指明了方向。也正因为此，在希尔伯特的墓碑（图20）上，便镌刻着他在国际数学家大会上的演讲金句：“我们必须知道，我们必将知道！”（Wir mussen wissen. Wir werden wissen）

陈景润的墓碑

陈景润是我国数学界的一位传奇式人物（图21）。他虽不善言辞，可在数学研究方面，特别是对哥德巴赫猜想的研究出类拔萃，一直处于世界领先地位。-

哥德巴赫猜想源于德国一位中学数学教师哥德巴赫，他依靠试验、观察发现：任何一个偶数（除了2，它本身就是一个质数）都能表示成两个质数（也称素数）之和。如4=2+2，6=3+3，8 = 5 + 3，1 0 = 5 + 5，1 2 = 5 + 7，14=7+7，16=13+3，18=13+5，20=13+7，……100=97+3，等等。不过，作为数学教师，他也知道试验并不是证明，这个命题是否正确必须经过严格的论证。于是，他在1742年6月7日写信给当时的数学大师欧拉，说他相信“任何一个大于2的偶数，都可以分成两个素数的和”，希望欧拉能帮他证明。欧拉于同年6月30日回信，说他相信这个猜想，但他还不能证明。

图21