基于重叠边界的有限元与离散元耦合异步长并行计算方法
2023-06-20金先龙王小卫潘浚铭杨培中
李 佟 金先龙 王小卫 潘浚铭 杨培中
(1.上海交通大学机械与动力工程学院, 上海 200240;2.上海交通大学机械系统与振动国家重点实验室, 上海 200240;3.上海航天精密机械研究所, 上海 201600)
0 引言
计算机硬件技术的发展使大规模复杂力学问题的数值计算更加高效[1]。有限元法(FEM)[2]和离散元法(DEM)[3]分别是能够获得结构宏观响应和细观演化两种不同尺度的重要数值方法。面对复杂的力学问题,结合两种算法的优势实现多尺度耦合计算对提升计算效率意义重大[4-6]。充分发挥计算机硬件资源优势,结合高效的数值算法,将计算模型进行区域分解[7]开展异步长计算,针对不同区域采用各异的计算方法[8]解决大规模力学问题也是进一步提升数值模拟计算效率的一个突破点。
很多学者研究了有限元与离散元耦合多尺度计算,取得了重要进展[9-14]。在上述研究中,采用区域分解的方式在一定程度上缩短了计算时间,然而这些工作往往由于算法稳定性限制[15-16]而使整个模型须采用单一的最小积分时间步长。异步长计算方法可有效改善单一积分时间步长造成的效率低下问题,早期的研究者主要有SMOLINSKI[17]和BELYSCHKO等18],研究对象多针对两分区结构动力学求解。MAHJOUBI等[19]引入拉格朗日乘子约束位移连续研究结构动力学问题的多分区多时间步长算法。LINDSAY等[20]采用域分解和多时间步长方法,在断裂区域采用细化网格研究了断裂力学问题。陈丽华等[21]研究了混合时间步长显式积分并行算法解决冲击动力学问题。马志强等[8,22-23]基于节点划分和重叠边界研究了结构动力学的显式多时间步长并行算法和显隐混合异步长交错计算方法。
目前异步长方法的研究多应用在求解有限元问题,对离散元及其耦合格式相关的异步长计算方法报道较少。MARSHALL等[24-25]在对气溶胶的力学行为研究中,提出了离散元多时间步长计算方法,其在流体计算、颗粒粘接计算和颗粒碰撞计算中分别采用3种不同的积分时间步长。CHAUDRY等[26]研究了颗粒材料的破碎问题,通过在全部-局部框架中采用不同积分时间步长解决了由于粒子运动不稳定导致的临界时间步长减小的问题。文献[24,26]均利用异步长算法缩短了整体计算时间,但是对于不同步长比下方法效率并没有做深入的研究。张锐等[27-28]基于元/网格动量传递的动力学过渡算法建立了有限元与离散元耦合的时间与空间多尺度计算模型,该方法在边界耦合过渡区含有多层离散单元,耦合区自由度较多且离散单元尺寸与有限元网格尺寸有关。而且上述研究中采用的都是串行的求解格式,事实上,多核并行计算对于提升多尺度问题计算效率同样具有重要作用[29]。
本文基于重叠边界提出一种改进的FEM-DEM耦合异步长并行计算方法,分析不同步长比的串行和并行求解格式的计算效率。将系统模型进行区域分解,针对分区计算类型采用合适的积分时间步长[30]。将重叠边界数据连续性传递引入到并行计算中,利用动态重叠边界方法和进程间通信来传输相邻子域之间的边界信息。边界数据传输过程中不涉及插值、截断过程,在保证计算精度的同时有效提升数值计算效率。
1 FEM-DEM耦合模型建立
1.1 显式有限元求解格式
在有限元计算中,含阻尼的线弹性结构动力学方程可以写为[31]
(1)
式中M、C、K——质量矩阵、阻尼矩阵和刚度矩阵
F——外载荷向量
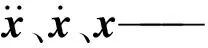
有限元求解中采用预测校正格式的Newmark积分格式,预测校正格式求解过程分为预测步、加速度求解以及校正步3个求解过程[32]。预测步中,第n+1时间步节点位移以及速度预测值可以由第n时间步节点的位移、速度以及加速度表示为
(2)

β、γ——Newmark时间积分控制参数,取β=0.25,γ=0.5
Δt——积分时间步长
此时方法具有二阶精度,是无条件稳定的[33]。将式(2)代入到式(1)求出第n+1时间步节点加速度,表示为
(3)
式中Fn+1——第n+1时间步外载荷向量
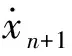
(4)
1.2 颗粒离散元求解格式
离散元算法[34]中离散单元遵从牛顿第二定律,即
(5)

Fij——作用在单元i的相邻单元j对它的作用力
Fi——作用在单元i的外载荷力
Ni——与单元i相邻发生作用的所有单元数量
N——系统中参与计算的所有单元数量
为了使离散元法准确描述材料的连续介质力学特性,采用连接键[35]形式的离散元法来处理连续介质力学问题。将连续介质离散成若干个携带质量、位移、速度和加速度的离散单元(本文称为颗粒),每个颗粒视为连续介质中的一个等效质点,通过相邻颗粒之间设定的连接键来表示两个颗粒之间的相互作用关系,实现连续介质的力学特性表达。
本文设定颗粒之间是弹性相互作用,通过连接两个颗粒之间连接键的变形来表示颗粒的相对运动,所有颗粒的运动即为连续介质宏观的特性。为了计算便捷,假设在整个计算过程中弹性系数等都保持不变,忽略加载历史和颗粒变形等。
为了统一耦合模型的求解格式,采用velocity-Verlet[36]显式积分算法来求解颗粒的运动方程,即
(6)
式中xi(n+1)——单元i第n+1个时间步位移
vi(n+1)——单元i第n+1个时间步速度
ai(n+1)——单元i第n+1个时间步加速度
fi(n+1)——单元i第n+1个时间步合力
xi(n)——单元i第n个时间步位移
vi(n)——单元i第n个时间步速度
ai(n)——单元i第n个时间步加速度
1.3 有限元离散元耦合求解格式
在有限元求解格式中,将式(1)写成如下形式
(7)
其中
在离散元求解格式中,将式(5)转换为
(8)
其中
比较式(7)和式(8),可以看出在两种不同的计算方法中,运动方程在求解形式上保持一致,可以将两种不同的方法耦合到一个计算程序中[5]。
2 交替格式的耦合异步长并行计算方法
耦合求解格式也适用于多个计算分区多核的求解过程[23],为了方便描述,以有限元和离散元两个计算分区为例进行异步长并行计算,采用边界重叠计算单元的形式实现一个系统时间步内有限元和离散元区域边界数据信息交换。
2.1 基于重叠边界的区域分割
将整个计算系统划分为有限元和离散元两个计算子分区,在有限元分区中,将参与计算的节点分为外部节点、边界节点和内部节点[8]。在离散元分区中,将参与计算的颗粒分为外部颗粒、边界颗粒和内部颗粒3类。其中有限元的边界节点和外部节点与离散元的外部颗粒和边界颗粒分别对应,构成重叠边界区域,用于边界数据传递,如图1所示。在有限元异步长计算中,需要多重的外部节点来保证在同系统时间步时边界节点数据可以完整求出[8]。相比于单纯的有限元多重节点的划分,本文提出的方法在传递边界数据时只有各自的一层外部节点(颗粒)和边界节点(颗粒),这是因为在离散元计算中,通常假定颗粒只与和它相邻的颗粒发生接触,即只有最近邻颗粒会发生接触,不考虑次近邻和其他近邻的颗粒。在有限元计算中,节点只与和它相邻的节点才会对总体刚度矩阵起作用。与多重节点方法相比,算法更加简洁高效,可操作性更强。
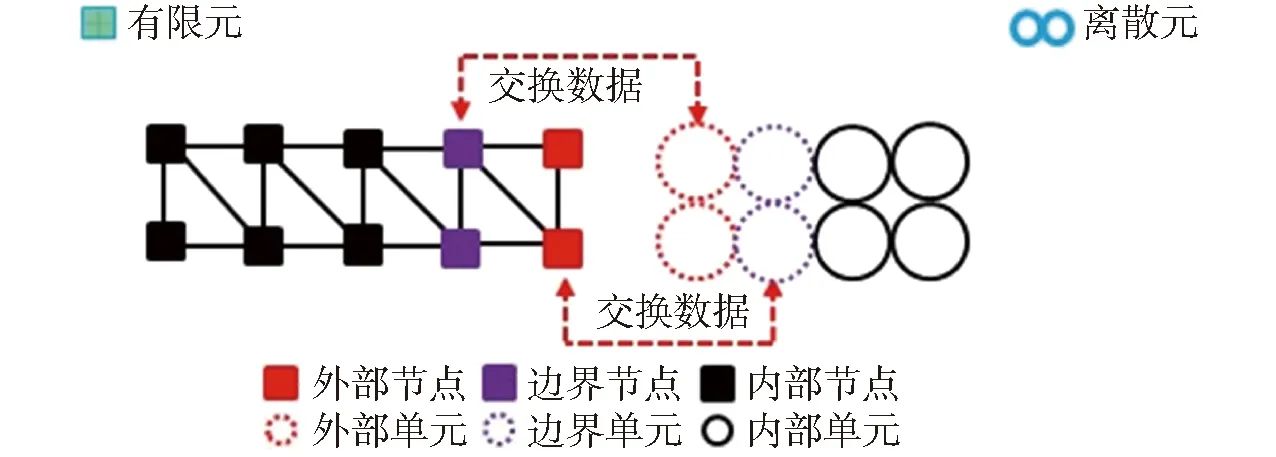
图1 重叠边界有限元-离散元分区示意图Fig.1 FEM-DEM partitioned schematic with overlapping boundary
2.2 并行计算方法
目前并行计算已经成为模拟当中重要的手段,尤其是大规模多自由度计算,采用并行计算可以发挥多核计算机优势提高计算效率[37-38]。由于有限元和离散元均采用显式计算格式,显式算法具有解耦特性(求解下一时刻的相关信息只需用到相邻节点上一时步的相关信息),这种求解格式的解耦特性使得程序具有天然并行性,为并行化计算提供了便利[22]。通过MPI[39]进行并行计算,单个计算进程负责一个计算分区的任务处理,在单个计算区域内部同时包含该区域内部和区域边界的计算信息,通过相邻计算区域的信息传递来保障系统数据的准确性和连续性。
并行算法性能常用加速比[40]来进行衡量。考虑不同步长比时的加速比,计算式为
(9)
式中t1——同步长时(即步长比为1时)计算时间
tη——步长比为η时的计算时间
2.3 交错格式异步长并行计算流程
一般有限元的积分时间步长条件比离散元条件宽松,因此本文离散元采用小步长,有限元采用大步长。一个完整的系统时间步包含一个有限元分区时间步和多个离散元分区时间步。计算时间步长分别为Δt和Δtr,满足Δt=ηΔtr(本文η均为整数)。为了描述异步长并行算法的计算流程,以步长比η=2进行说明,有限元分区(分区1)和离散元分区(分区2)各自采用CPU的一个进程去进行计算。分区2完成一个时间步的计算时,分区1并没有任何动作,当分区2又进行了一个时间步的计算后,此时分区1根据分区内部设定的计算时间步长完成一次计算,整个计算时间步也达到了一个系统时间步。图2为步长比η=2时,分区1和分区2中子循环时间步和系统时间步的并行计算流程。非重叠形式的异步长方法,边界位移、速度和加速度均假定为时间的线性插值函数,根据位移、速度、加速度与时间的关系,假定加速度成线性变化,通过积分速度为时间的二次函数,而位移则为更高的三次函数,在处理边界信息时会引起数据的不一致性[32]。因此在处理边界信息时通过MPI通信协议将两个进程内分区1和分区2重叠边界处的位移和速度信息进行传递和互换。

图2 耦合形式的异步长并行求解流程Fig.2 Parallel computing process of coupled multi-time step
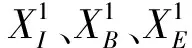
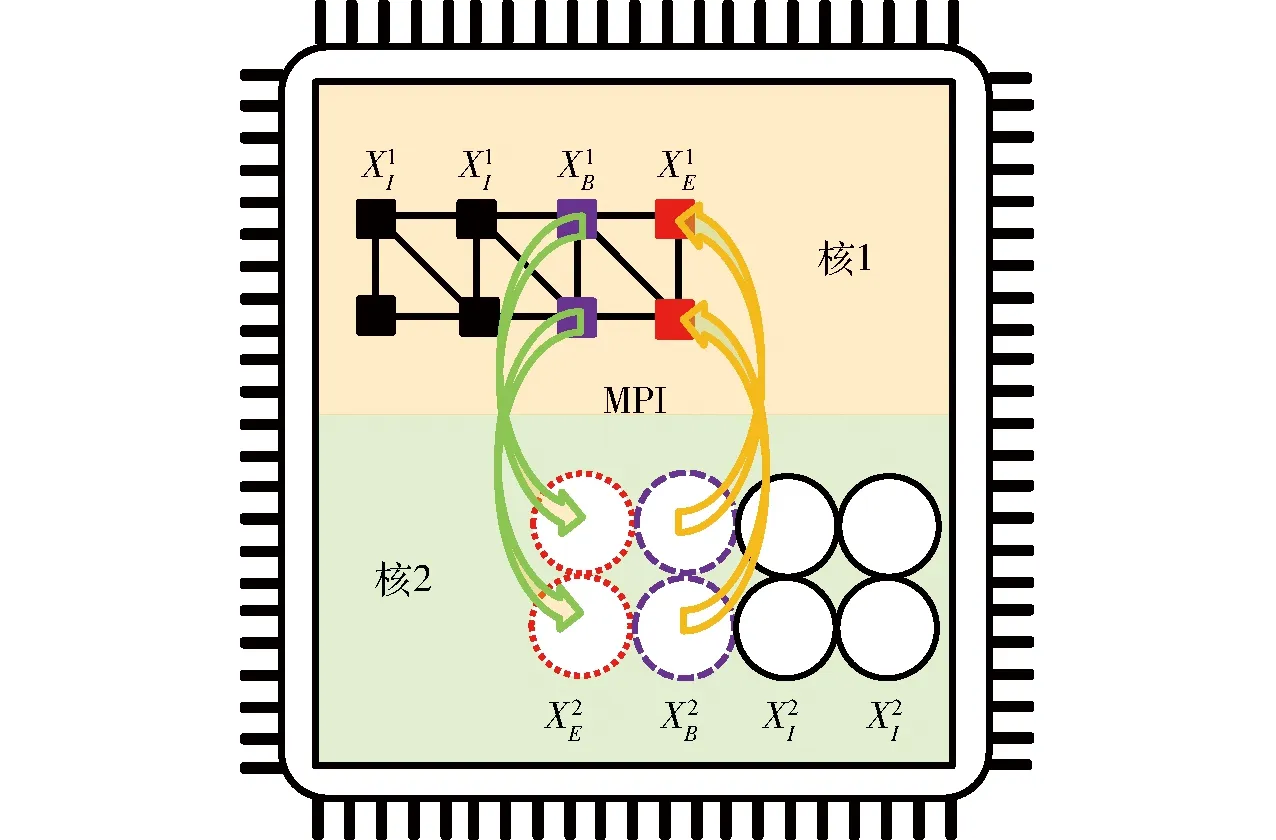
图3 不同分区边界信息传递示意图Fig.3 Schematic of boundary information transmission in different subdomains
在有限元计算中,刚度矩阵往往是具有一定带宽的稀疏对称矩阵,求解加速度过程中涉及矩阵求逆。采用稀疏矩阵的行压缩CSR存储格式[41]有较好的存储和求解效率。因此本文处理有限元分区计算过程采取稀疏矩阵求解的格式。而离散元求解直接根据节点自由度编号形成方程,采用坐标存储对应节点的信息即可。
3 精度验证
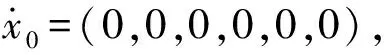
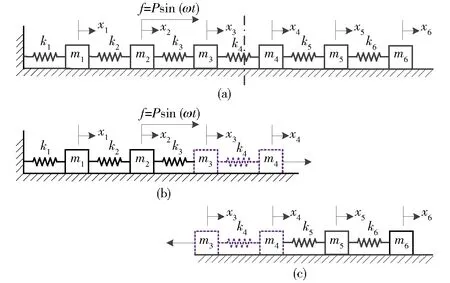
图4 6自由度弹簧-质量系统Fig.4 Six-DOF spring-mass system
离散元分区采用的时间步长为1×10-4s,有限元分区采用的时间步长为1×10-4η。取质量块3的位移作为参考。图5为采用不同步长比时与解析解的对比结果。从图5可以看出,节点位移曲线基本重叠,几种不同的方法都可以准确地计算出质量块3位移,表明本文开发的有限元-离散元耦合异步长算法能够满足计算精度。

图5 不同方法计算出的质量块3位移曲线Fig.5 Mass-3 displacement calculated by different methods
采用相同步长比(η=5)下串行和并行求解进行对比。质量块3的位移误差(不同方法减去理论值结果)如图6所示。从图6可以看出,有限元-离散元耦合形式的异步长算法在相同计算时间步长、步长比的条件下并行计算误差和串行计算误差相比没有发生变化,反映本文提出的分区并行数据传递策略的有效性。
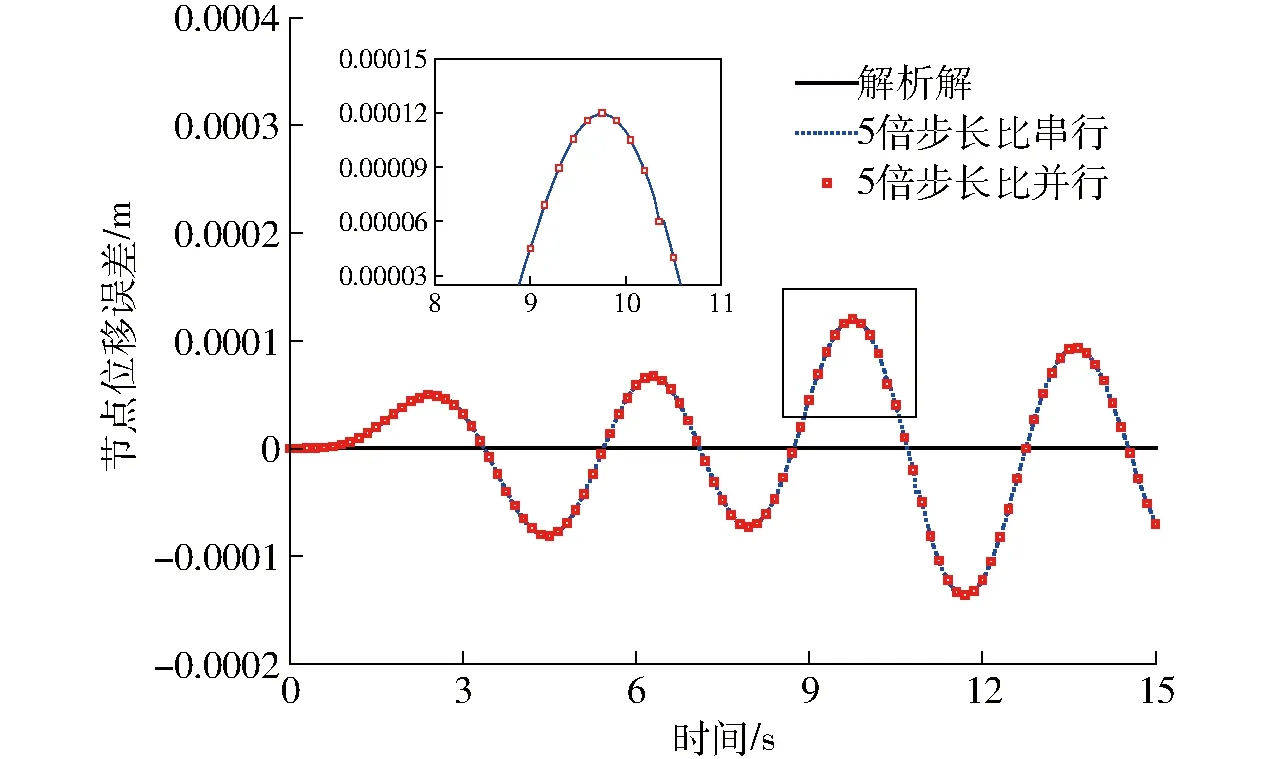
图6 质量块3位移误差曲线Fig.6 Displacement error curves of mass-3
4 数值算例和有效性评价
为了进一步验证算法在精度和并行效率方面的特性,采用超材料抵抗冲击载荷作为数值算例。基于质量-弹簧微结构超材料模型[42],研究超材料对于冲击载荷起到的衰减作用。超材料系统区域分解及施加的脉冲载荷如图7所示。超材料微结构由外壳和内部的谐振子构成,质量分别为ms和mv;谐振子与外壳之间的谐振子弹簧、外壳之间弹簧刚度分别为ks和kn。谐振子、外壳及谐振子弹簧共同组成一个超材料微结构,当满足一定条件时,等效成为负质量实体[43],可以对冲击载荷起到衰减作用。
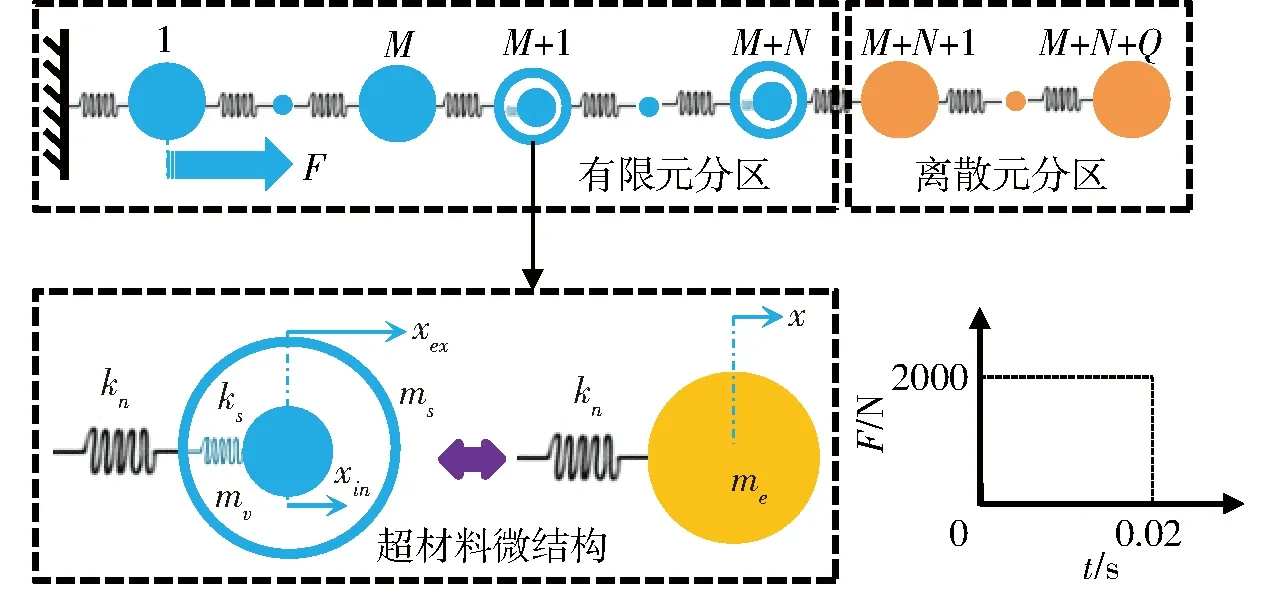
图7 超材料系统区域分割及载荷历程Fig.7 Metamaterial system domain partition and load history
超材料微结构的动力学方程为
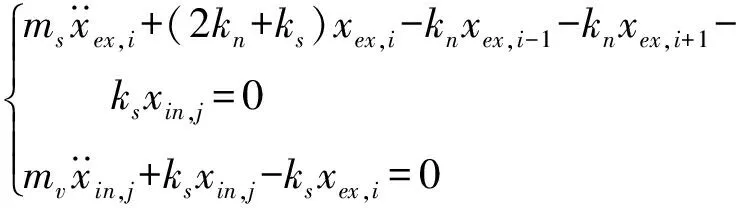
(1≤j≤N,i=j+M)
(10)
将整个计算模型划分为有限元(分区1)和离散元(分区2)两个计算分区,系统仿真计算时间设定为75 ms。一个超材料微结构自由度为2个,为了使各分区参与计算的自由度数量相等,因此M=100,N=200,Q=500,计算参数设定为:ms=0.05 kg,mv=0.05 kg,kn=7.8×106N/m,ks=2.49×106N/m。离散元分区计算中的积分时间步长设定为1×10-4s。当系统中没有超材料结构时,系统由M+N+Q个实心颗粒组成。图8为采用不同方法获得的离散元分区中第250号颗粒的时域波形(位移与最大位移之比)。从图8可以看出,超材料显著降低了结构位移响应幅值。当步长比η=5时,所提出的有限元-离散元耦合异步长并行计算方法与Newmark[44]方法获得的位移响应一致,验证了本文所提出方法的有效性和精度。
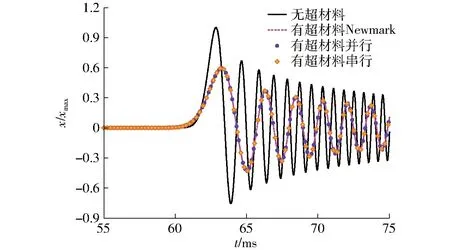
图8 离散元分区中第250号颗粒的时域波形图Fig.8 Time domain waveform of 250th particle in DEM domain
对于异步长算法而言,分区步长比、串行及并行格式都会影响计算效率。为了研究算法在不同步长比条件下的计算效率,统计采用多组步长比时消耗的时间,结果见表1。从表1可以看出,随着步长比的增加,计算总时间逐渐减少,算法的加速比增加,步长比达到20时的计算时间缩短为步长比为1(同步长)时的65.6%。由于在计算过程中,采用异步计算模式,在未达到一个系统时间步内,分区2进行多次计算;当达到一个系统时间步内,分区1进行一次迭代计算,提高步长比意味着在分区2步长不变的情况下,分区1采用更大的计算时间步长,从而降低了分区1的迭代次数,因此分区1计算时间有所缩减,进而提高了整体计算效率。

表1 不同步长比下串行计算时间Tab.1 Computing time with different time-step ratios
图9为相同步长比条件下采用串行格式与并行格式所消耗的求解时间。可以看出,随着步长比的增加,采用并行格式的求解时间逐渐降低,这与串行求解格式下得到的结论一致。在相同步长比时,采用并行求解格式的计算时间低于串行求解格式的计算时间,也就是说采用异步长并行求解格式,在串行异步长算法基础上,使得计算效率又得到了进一步的提升。从图9也可看出,当步长比达到5以上时,继续增加步长比,并行计算消耗的时间并没有明显降低,而是维持在一个稳定状态。
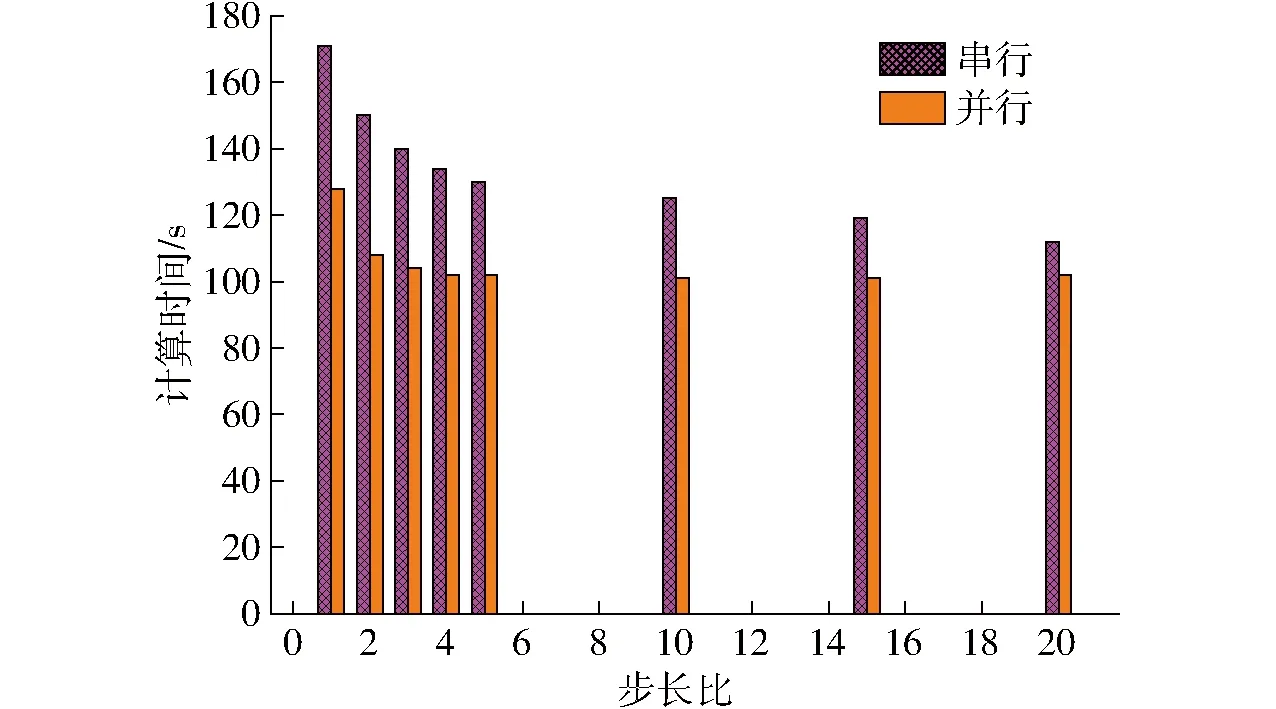
图9 不同格式下的计算时间Fig.9 Calculation time in different formats
从计算结果来看,随着步长比的增加,无论是串行格式还是并行格式的计算时间与时间比率的下降幅度都在逐渐减小,计算时间并不会随着步长比增加而一直保持相同的速率下降,而是趋于一个稳定值。这是因为在一个异步通信周期内,进程之间等待时间过长,出现了明显的分区负载不均衡现象。分区计算负载不平衡在一定程度上阻碍了计算效率的提升,因此研究适用于有限元和离散元耦合的负载均衡算法,采用更多核数的并行计算可以进一步提升多时空多尺度异步长算法性能。
5 结论
(1)所有分区均采用相类似的显式积分算法求解格式,通过数据切分和MPI通信协议充分发挥多核计算机性能优势,边界信息传递只与相邻的分区有关,提高了并行计算过程信息传递效率。
(2)传递过程中不涉及位移和速度插值、截断等,有效地提高了计算精度。相比于单纯的有限元多重节点的耦合策略,重叠区域范围小,数据传递量小,传递效率高。
(3)重叠区域只有两层节点(颗粒),各分区根据自己的单元特征选择适合的时间步长,突破了以往有限元-离散元耦合计算采用多层过渡区域的限制。
