基于目标导向采样的机器人改进概率路图法研究
2023-06-20陈志勇吴精华
陈志勇 吴精华
(福州大学机械工程及自动化学院, 福州 350108)
0 引言
为提高工作效率、保证任务质量,机器人路径规划问题研究一直深受人们的重视。目前,路径规划方法主要包括Dijkstra 算法[1-3]、A*算法[4-6]、人工势场法[7-10]、快速扩展随机树(Rapidly exploring random tree, RRT)[11-13]、概率路图法(Probabilistic roadmap method, PRM)[14-16]等。
Dijkstra算法[17]虽然在地图中可以找到一条全局最优路径,但会扩展出大量冗余的节点,导致搜索时间大量增加。而A*算法、人工势场法等算法虽在二维路径规划中有着不错的效果,但随着维度增加、空间复杂度提升,算法整体计算量骤增,并可能陷入局部最优值。RRT算法是一种基于随机采样且可用于高维空间下的路径搜索法,但RRT算法存在偏离最优解、局部扩展缓慢等问题,如文献[18]提出了基于双向搜索树的RRT-Connect算法,该算法虽可有效提高搜索效率,但在复杂环境中仍然存在随机性强、难以找到路径等问题。与RRT算法类似,PRM算法亦是一种基于随机采样的路径规划算法,该方法同样有助于机器人在高维空间中寻找到一条可行路径,且具有计算量小、实时性好等优点,已被广泛应用于各类机器人的路径规划。不过值得注意的是,传统PRM算法采用的是完全随机的采样策略,为保证算法搜索效率,当采样点数量一定时,若其中的多数随机采样点刚好落在障碍物空间中,则会使自由空间中的采样点数变少,地图连通性降低,可能会导致搜索路径失败;尤其当遇到狭窄通道或者大量障碍物时,传统PRM算法将更难在工作空间中规划出一条可行路径。为了解决这一问题,最直接的方法就是重新采样并增加更多的采样点,使之在自由空间的采样点数量增多;但该方法难以确定有效增加在狭窄区域的采样点,反而会使路径规划整体时间呈指数性增长,并大大降低其实时性。为此,近年来许多学者针对PRM算法又提出了各种改进方法。如文献[19]提出了高斯采样方法,高斯采样是基于障碍物的密度使得狭窄区域中的采样点有效增加,但高斯采样法会在障碍物附近增加许多不必要的节点,造成了节点浪费。文献[20]提出了一种桥梁测试方法,该方法从障碍物中提取两个采样点,如果两个采样点的中点位于自由空间中,则将该点加入到自由点集;该方法虽可有效增加狭窄区域的采样点密度,但会有较多的路标分布在障碍物凹陷处和拐角处,导致路径规划效率变低。
为实现机器人在具有狭窄通道工作环境下的有效路径规划,本文提出一种融合全局目标导向采样、局部节点增强的Improved PRM算法。该算法采用基于全局目标导向采样及随机采样的混合采样方式来提高全局采样点落在狭窄通道内的概率,以实现启发式地图增强;利用节点权重思想提取位于狭窄区域的节点,并在提取的节点周围通过高斯分布来扩展其附近的节点,以增强地图连通性,提高算法路径规划成功率;通过冗余节点剔除策略,有效减少路径节点数及路径代价,实现算法的路径优化。通过仿真对比实验,对Improved PRM算法在机器人路径规划上的可行性及有效性进行验证。
1 PRM基本原理及六自由度机器人模型
1.1 PRM基本原理
作为解决高维空间下机器人路径规划问题的主要方法之一,基于全局随机采样及图搜索的PRM算法的实现主要分为离线学习阶段和查询阶段。
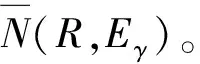
查询阶段是指在给定的起始位置和目标位置的条件下,根据离线学习阶段得到的无向路径图上,采用A*算法在起始点和目标点之间搜索到一条可行的无碰撞路线。
1.2 六自由度机器人运动学模型
本文以一种六自由度机器人作为 Improved PRM算法的应用对象。该机器人具有6个旋转自由度θj(j=1,2,…,6),且θj表示机械臂连杆j相对于前一个连杆j-1的关节角。据文献[22],机器人末端操作器连体坐标系相对于基座连体坐标系的齐次变换矩阵为
(1)
其中
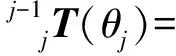
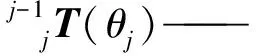
αj-1——连杆j-1与连杆j间的连杆扭角
aj-1——连杆j-1的长度
dj——连杆j-1与连杆j公法线间的距离
n、o、a——机器人末端操作器的姿态
p——机器人末端操作器的空间位置
利用式(1)对机器人进行逆运动学求解,可容易将其末端操作器位姿映射到系统各关节转角θj(j=1,2,…,6)上(即反解出机器人各关节转角)。显然,机器人末端操作器的路径规划问题可以转换成关节空间层面上的路径规划问题。
2 融合全局目标导向采样、局部节点增强的Improved PRM算法
受采样随机性的限制,传统PRM算法在狭窄通道的通过性往往较差。考虑到机器人在特殊情况下又需要经过指定的狭窄通道进行操作,若直接采用传统PRM算法对此类机器人进行规划,则算法的成功率将难以得到保证。为此,本文将在传统PRM算法框架的基础上,着重对其学习阶段的无向图构建方式进行改进,提出一种基于全局目标导向采样、局部节点增强、冗余节点剔除的机器人Improved PRM算法,并将该算法应用于平面栅格地图场景及六自由度机器人路径规划。
2.1 基于全局目标导向采样的启发式地图增强方法
为构建一幅无向图,传统PRM算法采用全局随机采样,由于此种采样方式过于随机、单一,在机器人工作空间的狭窄通道中很难获取足够的采样点,因此所得的无向图连通性较差,难以保证后续路径搜索成功率。为此,本文引入了一种目标区域导向采样规则,并将其与随机采样方式相结合,作为Improved PRM算法的全局采样方式。首先,以机器人在给定工作空间中的始末位置分别作为算法采样的起始节点及目标节点;接着,从起始节点往目标节点方向确定采样目标区域,并在该区域进行合理的导向采样预处理,以获得一定数量的全局导向采样点,提高采样点落在狭窄通道中的概率;最后,再在工作空间中进行惯常的随机采样,来获得剩下的全局采样点。
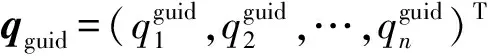
qguid=qstart+D0Frf
(2)
其中
Frf=(r1f1,r2f2,…,rnfn)T
式中D0——从起始节点往目标节点方向辐射采样的算法调控系数
Frf——导向性采样函数列向量
ri——第i(i=1,2,…,n)维方向上变量的采样步长
fi——第i(i=1,2,…,n)维方向上变量的采样函数
通过设计不同形式的采样步长ri及采样函数fi来获得各种满足特定采样规则的导向性采样节点。在获得导向采样点后,对采样点进行是否处于自由空间的判定。若该采样点刚好落在障碍物空间中,则舍去该节点;反之,则将其加入到自由节点集R中。
剩下的全局采样点,采用随机采样方式,即
qrand=qmin+(qmax-qmin)rand[0,1]
(3)
其中
式中qrand——通过随机采样得到的n维采样节点
qmin——由节点各维变量在工作空间中所能取到的最小值组成的列向量
qmax——由节点各维变量在工作空间中所能取到的最大值组成的列向量
rand[0,1]——在[0,1]内选取的随机数
类似地,在获得全局随机采样点后,对采样点进行是否处于自由空间的判定。若该采样点刚好落在障碍物空间中,则舍去该节点;反之,则将其继续加入到自由节点集R中。
2.1.1方法在平面栅格地图场景中的实现
文献[23]提出了一种目标导向采样方法,该方法可实现无人机在特定起始点和特定目标点连线方向上的目标区域外扩辐射圆导向采样;不过由于受采样规则限制,该算法采样时引导方向单一,应用灵活性受到限制。为此,拟通过式(2)中调控系数D0来对原采样规则进行修正,使修正后算法的导向性更加灵活、实用。
为实现平面栅格地图场景下目标区域的导向采样,定义地图左上角位置为原点,地图水平方向为x轴方向(水平朝右为正向),垂直方向为y轴方向(垂直朝下为正向),起始节点、目标节点及导向采样节点分别为qstart=(xstart,ystart)T、qgoal=(xgoal,ygoal)T及qguid=(xguid,yguid)T。于是,始末两节点连线方向与x轴正向的偏角α可表示为
(4)
其中,α∈(-π/2,π/2),以顺时针转向为正,且当xstart=xgoal时,α取π/2。
为实现在栅格地图下的均匀外扩辐射圆采样,设计采样函数列向量Frf为
(5)
其中r1=r2=R0m=-i0+1,-i0+2,…,i0-1
式中R0——辐射圆的外扩步长
m——辐射圆心角控制系数(i0≤k,且i0选取越大,圆心角就越大;反之亦然)
i0——m取值范围的调节参数
k——辐射圆上的采样点数(k取值越大,则在起始点和目标点连线附近的采样点越密集,在自由空间中的采样占比越大;反之亦然),取k>0
n0——外扩的辐射同心圆序号,n0=1,2,…,N
其中辐射圆总数N计算式为
(6)
式中 Int[ ]——对计算结果的取整函数
为使采样算法可以自动根据始末节点在平面栅格地图中的具体位置进行方向调控,选取调控系数D0为
(7)
其中A=(xgoal-xstart,ygoal-ystart)TB=(1,0)T
式中A——从起始节点qstart到目标节点qgoal的方向矢量
B——x轴基矢量
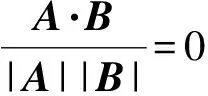
在随机采样方面,平面栅格地图的随机采样点可表示为qrand=(xrand,yrand)T,取式(3)中的qmin=(0,0)T,qmax=(V1,V2)T。其中,V1、V2分别为栅格地图水平及垂直方向上的维度。
2.1.2方法在六自由度机器人中的实现
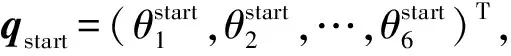
(8)
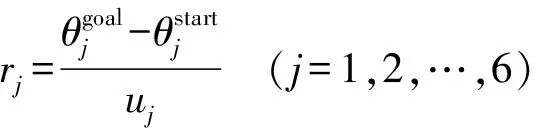
式中rj——机械臂第j个关节的采样步长
uj——用于第j个关节始末角度等分的正整数
rand[0,uj]——随机在0~uj中选取的整数,主要用于控制第j个关节在始末范围内的定向采样位置
2.2 基于高斯分布的局部节点增强策略
传统PRM算法利用局部规划器对自由节点集R中各节点与其邻域半径ρ0范围内的其他节点作碰撞检测,以获得各节点的邻域点集,进而得到无向图。前述基于全局目标导向采样的地图增强方法虽可在工作空间狭窄通道内增加一定的采样点,但数量仍有限且各节点间的连通性依然较差。为进一步提高算法连通性,有必要利用狭窄通道内已有节点来扩展出更多的狭窄通道局部新节点。为此,本文结合节点权重思想[24]对位于狭窄区域的节点进行提取,并给出一种基于高斯分布的局部节点增强策略。
设全局采样得到的自由节点集R包含有N1个节点,qγ表示第γ(γ=1,2,…,N1)个节点。首先,利用局部规划器在自由节点集R中所有采样点邻域内作碰撞检测;其次,根据碰撞检测结果,计算qγ位于狭窄区域的权重w(qγ)为
(9)
其中
式中P(qγ)——节点qγ的局部规划失败率
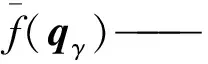
s(qγ)——局部规划器尝试连接节点qγ到其他节点的总次数
设狭窄区域权重判定阈值为w0,当w(qγ)>w0时,则可认为节点qγ位于狭窄区域内;反之亦然。最后,将所有位于狭窄区域的点放入狭窄区域节点集W中。
若狭窄区域节点集W共有N2个节点,则在点集W的各节点qζ(ζ=1,2,…,N2)周围通过高斯分布规律来扩展一定数量的新节点,即
qnew=qζ+gGaussian[0,1]
(10)
式中 Gaussian[0,1]——标准正态分布的随机数
g——n维高斯分布采样的范围幅值列向量
以此来增加狭窄通道中的节点数,增强狭窄通道的连通性。
对于新扩展出来的局部节点,去除位于障碍物空间的节点,保留位于自由空间中的节点,并将这些节点再次加入自由节点集R中。利用局部规划器再次对更新后的自由节点集R进行碰撞检测,得到各采样点的邻域点集Eγ,并最终得到更新后的无向图。
2.3 基于冗余节点剔除的路径优化策略
鉴于前述无向图中的多数节点仍是通过随机方式产生的,所以改进PRM算法若直接利用A*算法进行路径搜索,得到的初始路径将存在有较多的冗余节点。为了减少路径节点、缩短路径长度,Improved PRM算法通过剔除冗余节点、提取关键节点来优化A*算法得到的初始路径。
以图1为例进行简单说明。设图中黑色表示障碍物,A*算法得到的初始路径点集为Q={qstart,q1,q2,q3,q4,q5,q6,qgoal}(图中的黑色实线路径)。首先,以起始节点qstart为基础建立关键节点集Q′={qstart};之后,将关键节点qstart与初始点集Q中的后续节点进行连接,如果两个路径节点连线没有与障碍物干涉,则继续连接下一个节点;如果碰撞到障碍物,则把前一个节点放入到关键节点集Q′中,并把该节点作为新的关键节点与Q中剩余节点逐个进行尝试连接并进行相应的碰撞检测;重复以上步骤,直至遍历到目标节点qgoal;最后将得到的关键节点集Q′={qstart,q2,q5,qgoal}中的各节点依次连接起来,即可得到最终的优化路径(图中的虚线路径)。
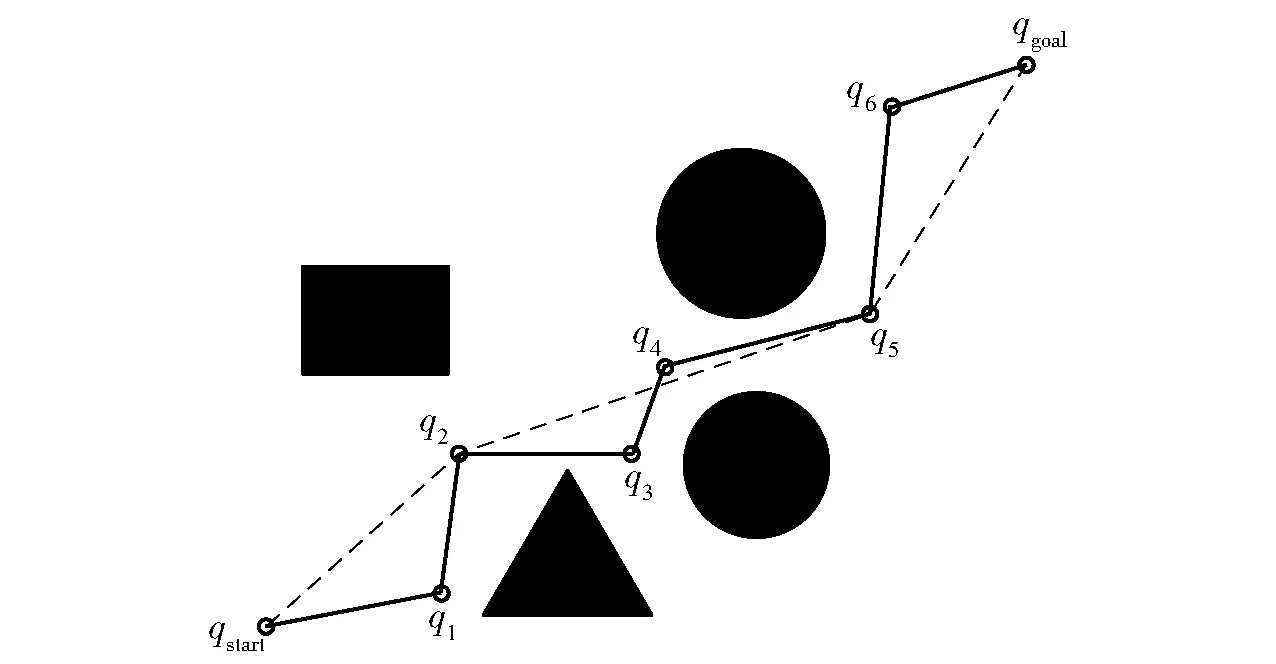
图1 冗余节点剔除示意图Fig.1 Redundant node removal diagram
2.4 路径规划实现步骤
Improved PRM算法的路径规划步骤如下:
(1)在工作空间中,设qstart为起始点,qgoal为目标点,算法邻域半径为ρ0。
(2)根据目标导向采样规则qguid=qstart+D0Frf,在工作空间中获得一定数量的目标区域采样点,并将其中位于自由空间的采样点加入到自由节点集R中。
(3)根据随机采样规则qrand=qmin+(qmax-qmin)rand[0,1],在工作空间中进行一定数量的随机采样,并将位于自由空间的采样点也加入到自由节点集R中。
(4)利用局部规划器对自由节点集R中每个采样点qγ和其邻域半径ρ0范围内的其他采样点的连线与障碍物作碰撞检测;若连线与障碍物干涉,则舍弃qγ与其邻域ρ0范围内采样点的连线;反之,则保留;遍历完qγ邻域范围内的所有采样点后,得到采样点qγ的邻域点集Eγ。
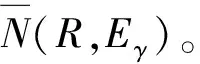
(6)计算自由节点集R中每个采样点qγ位于狭窄区域的权重w(qγ),若w(qγ)>w0,则将该点加入到狭窄区域节点集W;反之亦然。
(7)不断重复步骤(6),待遍历完R中所有节点后,得到最终更新后的狭窄区域节点集W。
(8)利用节点增强策略qnew=qζ+gGaussian[0,1]对点集W中的节点qζ进行周围新节点扩展,并将位于自由空间的新节点也加入到自由节点集R中。
(9)不断重复步骤(8),待遍历完狭窄区域节点集W中每个节点后,得到更新后的自由节点集R。
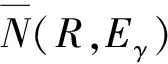
(12)使用冗余节点删除策略,删除初始路径中冗余的节点,得到最终路径。
3 仿真实验
首先对传统PRM算法、Gaussian PRM算法、RRT-Connect算法、Improved PRM算法在平面栅格地图场景中进行仿真实验,通过不同算法在路径规划成功率、时间、路径质量的分析来检验Improved PRM算法的有效性。其次,在ROS仿真平台上建立六自由度机器人仿真模型及具有狭窄通道的仿真环境,并将Improved PRM算法应用于机器人路径规划仿真实验。通过Improved PRM算法与传统PRM算法的仿真结果对比,证实所提算法的可行性。
3.1 平面栅格地图仿真实验
如图2所示,给定的平面栅格地图尺寸为500 mm×500 mm,图中符号“×”表示机器人起始点qstart=(1 mm,1 mm)T,符号“△”代表目标点qgoal=(450 mm,400 mm)T,狭窄通道用椭圆形框框出。实验中,RRT-Connect算法的采样步长设为50 mm,传统PRM、Gaussian PRM、Improved PRM算法在地图中的总采样点数均设为300个,邻域半径ρ0设为70 mm。同时,Gaussian PRM 算法中的高斯分布采样的范围幅值列向量设为g=(25.0 mm,25.0 mm)T;Improved PRM算法的其他参数设为R0=50 mm,g=(25.0 mm,25.0 mm)T,w0=0.015。在相同环境下,每种算法各进行150次仿真实验,仿真结果见表1。图2分别给出了传统PRM、Gaussian PRM、RRT-Connect、Improved PRM算法仿真中某次成功规划的路径图;需要指出的是,图2中绿色点均表示各算法通过随机采样得到的采样点,图2d中蓝色点表示全局目标导向采样得到辐射圆采样点,红色点为狭窄通道内通过局部高斯扩展出的采样点。在前述Improved PRM算法仿真中,利用狭窄区域节点集W中节点扩展出来的满足高斯分布的部分增强节点参数见表2。
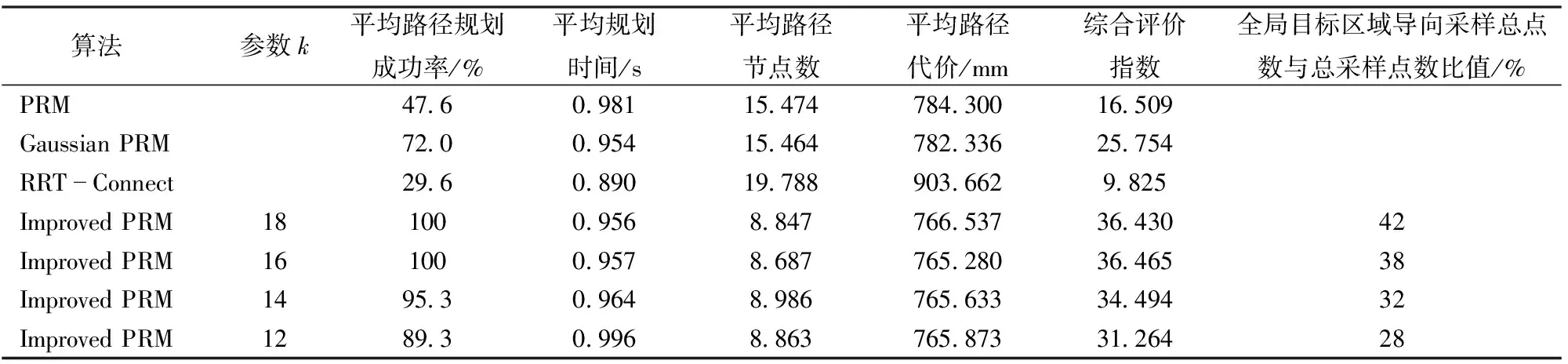
表1 4种算法仿真结果数据对比Tab.1 Comparison of simulation results of four algorithms
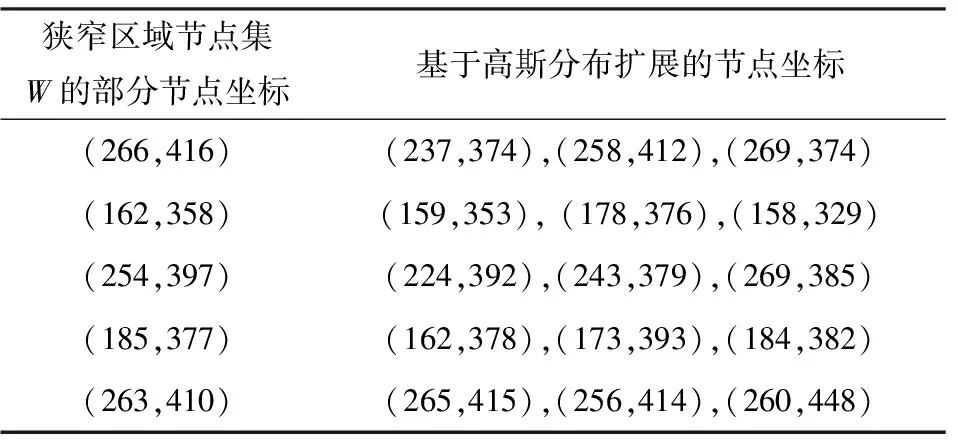
表2 基于高斯分布扩展的部分节点参数Tab.2 Parameters of some nodes extended by Gaussian distribution mm

图2 4种算法得到的路径图Fig.2 Path graphs obtained by four algorithms
为了判断算法规划路径的性能,定义综合评价指数E1为
(11)
式中S——算法路径规划成功率
Lmin——起始点到目标点连线的始末长度
Lnow——路径代价

由表1可知,RRT-Connect算法的路径规划成功率最低,只有29.6%,这说明RRT-Connect算法在这种存在狭窄通道的工作环境中较难规划出一条可行的路径。Gaussian PRM算法的成功率较传统PRM算法高24.4个百分点,说明Gaussian PRM算法可在一定程度上提高路径规划的成功率。由于采样密度不一样(即参数k选取),Improved PRM算法的成功率最高值为100%,最低值为89.3%,均高于其他算法,这说明Improved PRM算法可以大幅提高路径规划成功率。
在算法平均规划时间上,4种算法的平均规划用时差距不明显,传统PRM算法用时最多,RRT-Connect算法用时最少。所以在相同的环境下,Improved PRM算法在不多耗费时间的基础上,可以有效地提高机器人路径规划的成功率,保证算法路径规划的稳定性。
从综合评价指数来看,Improved PRM的综合评价指数均比其他算法高。Improved PRM综合评价指数最高值36.465比其他算法最高值25.754高41.59%,则说明Improved PRM较其他算法能够更有效地在具有狭窄通道的复杂环境中找到一条无碰撞的较优路径。从表1可知,当全局目标区域导向采样占比为32%~42%时,路径规划的成功率较高,综合评价指数也较高。
传统PRM、Gaussian PRM、RRT-Connect、Improved PRM算法均涉及随机采样,寻找的路径随机性较强,所以规划出来的路径会存在较多的冗余节点,导致机器人的运行时间会随之增加,因此优化路径质量显然很有必要。本文路径质量评价指数E2计算式为
(12)
式中Nsum——路径节点数
表3为4种算法得到的路径质量对比情况。由表3可以看出,RRT-Connect的平均路径代价最大,路径节点数最多,路径质量评价指数最低,仅有25.0%。Gaussian PRM的路径质量评价指数比传统PRM的路径质量评价指数高0.2个百分点,Improved PRM的路径质量评价指数最高值83.6%比Gaussian PRM高38.5个百分点,这说明Improved PRM找到的路径质量更优。
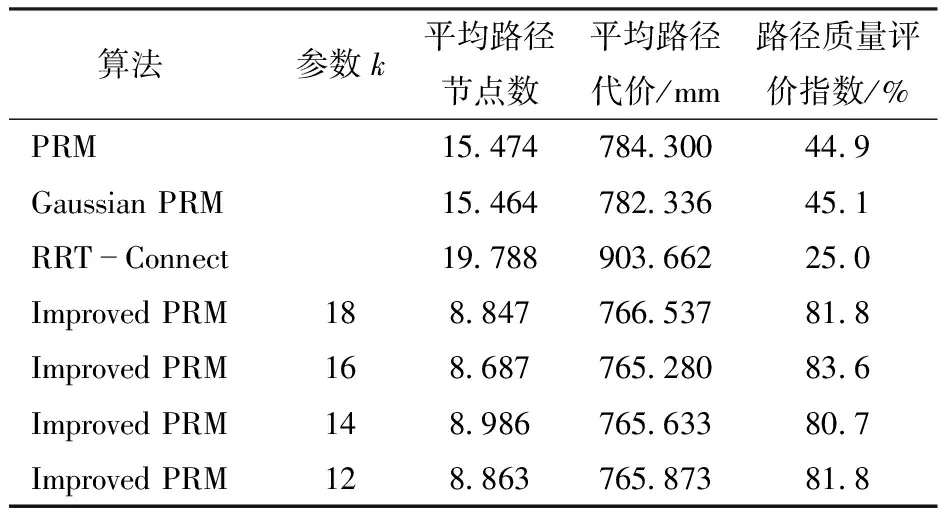
表3 路径质量对比Tab.3 Path quality comparison
上述分析可知,本文所提Improved PRM算法可以大幅地提高路径规划的成功率,有效减少路径节点数,降低路径代价,比传统的PRM、Gaussian PRM及RRT-Connect算法能够更容易地找到一条无碰撞的可行路径。
3.2 基于ROS平台的六自由度机器人仿真实验
为进一步验证Improved PRM算法的可行性,本文在ROS仿真平台中选用MOTOMAN-GP7型六自由度机器人作为仿真对象,该机器人的D-H参数见表4,同时构造具有狭窄通道的复杂仿真环境,见图3a;并继续利用Improved PRM及传统PRM算法对机器人做路径规划仿真对比实验。在图3a中,参考坐标系建立在机器人基座中心处,各障碍物形状、尺寸及位置信息见表5。

表4 MOTOMAN-GP7的D-H参数Tab.4 D-H parameters of MOTOMAN-GP7
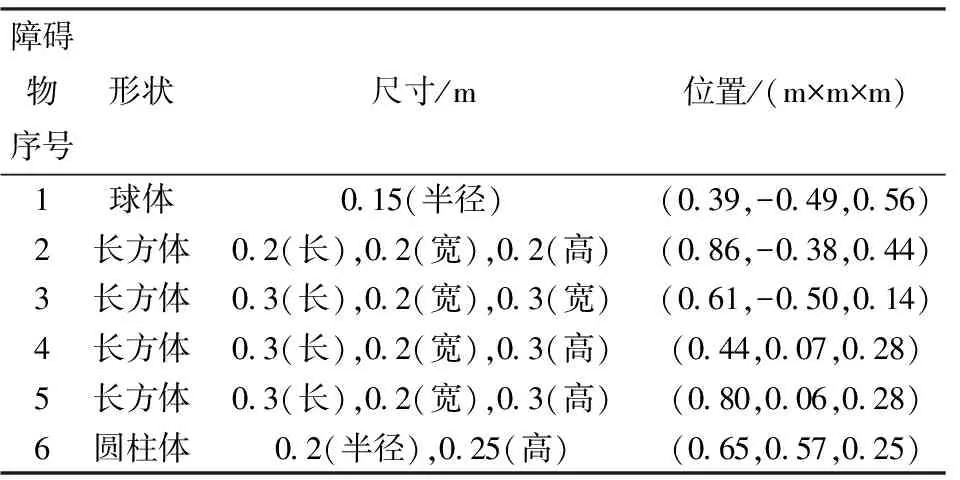
表5 障碍物信息Tab.5 Obstacles’ information
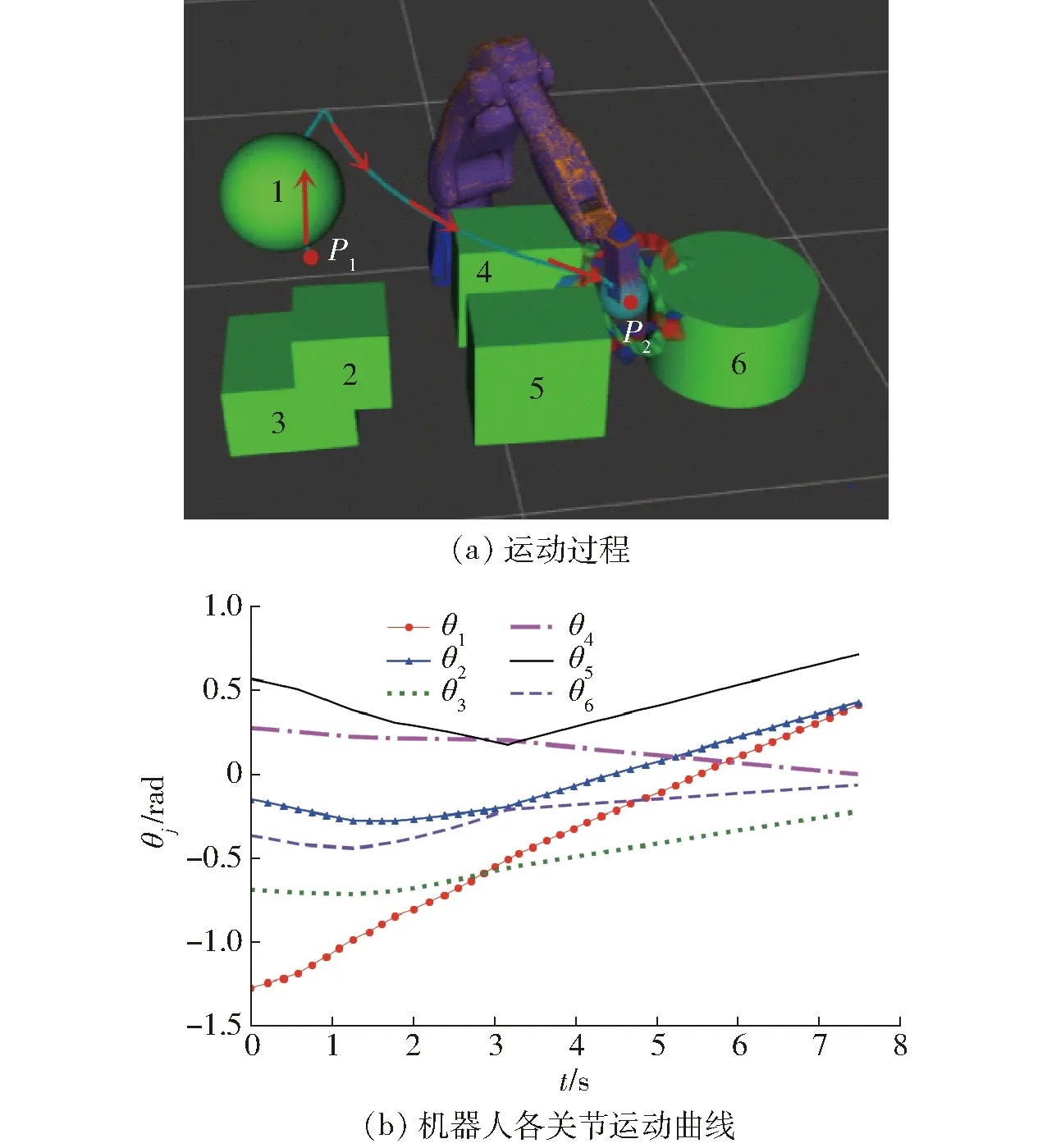
图3 传统PRM算法仿真结果Fig.3 Simulation results of traditional PRM algorithm
仿真时,要求机器人末端操作器从起始点P1(位置坐标为(0.17 m,-0.45 m,0.43 m)、RPY角为(0.13 rad,-3.13 rad,2.02 rad))尽可能经由障碍物2、4、5所形成的狭窄通道抵达目标点P2(位置坐标为(0.65 m,0.29 m,0.35 m)、RPY角为(-3.08 rad,-0.06 rad,0.41 rad))。为此,利用ROS平台的KDL逆运动学求解器将机器人末端始末位姿转换为关节空间下各关节的始末位置,进而得到算法的起始节点qstart=(-1.27 rad,-0.15 rad, -0.69 rad,0.28 rad,0.57 rad,-0.37 rad)T和目标节点qgoal=(0.41 rad,0.43 rad,-0.22 rad,0 rad,0.72 rad,-0.06 rad)T。
仿真时,传统PRM、Improved PRM算法的邻域半径ρ0均设为2 rad,此外,Improved PRM算法进行全局导向性采样概率设为37%,uj=6(j=1,2,…,6),w0=0.002,g=(0.8 rad,0.8 rad,0.8 rad,0.8 rad,0.8 rad,0.8 rad)T。
利用传统PRM算法及Improved PRM算法分别对ROS平台中的机器人进行50次成功的路径规划仿真实验,并记录下2种算法每次路径规划所得到的路径代价、规划时间及狭窄通道的通过频次。此外,为保证机器人能够平稳地从初始位置运动到目标位置,采用三次样条插值法来生成机器人各个关节的运动曲线[25]。图3为利用传统PRM进行某次路径规划得到的机器人运动过程图及各关节转角变化曲线,图4为利用Improved PRM进行某次路径规划得到的机器人运动路径图及各关节转角变化曲线。
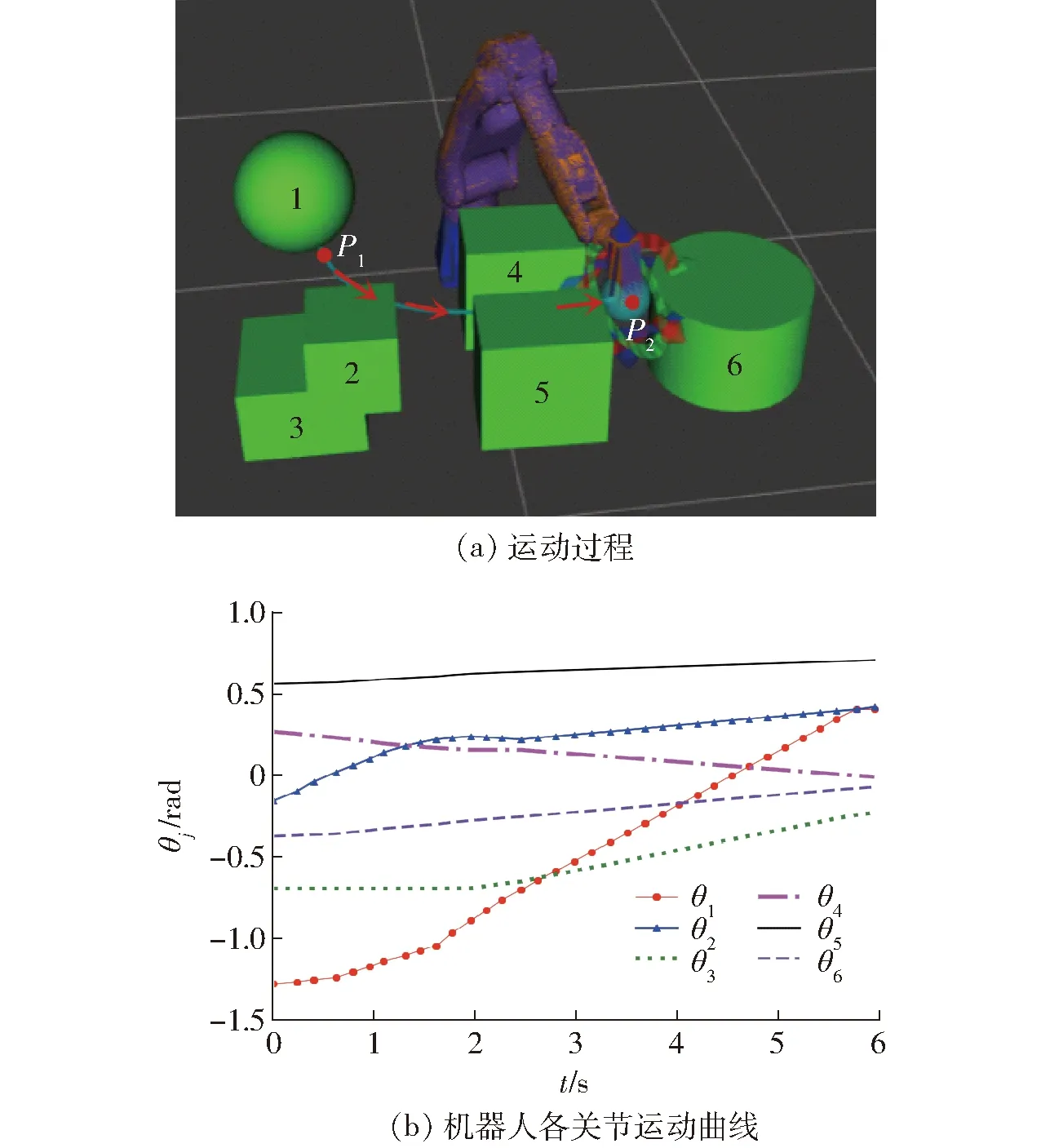
图4 Improved PRM算法仿真结果Fig.4 Simulation results of Improved PRM algorithm
利用曼哈顿距离定义机器人总路径代价为
(13)
式中Nz——每次路径规划得到的总节点数计算两种算法50次仿真实验的平均路径代价、平均耗时及通过狭窄通道次数,见表6。
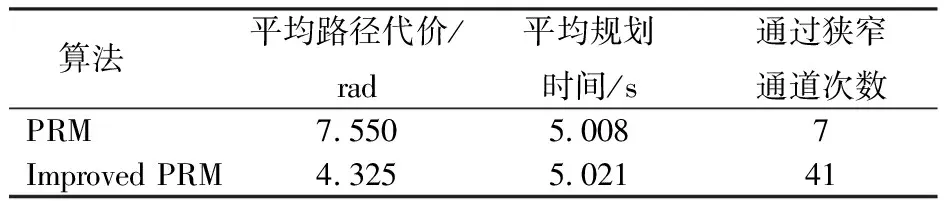
表6 两种算法仿真结果对比Tab.6 Comparison of simulation results of two algorithms
由表6可知,在50次仿真实验中,两种算法在平均路径规划时间上并无太大差别,但ImprovedPRM算法得到的平均路径代价比传统PRM算法降低42.7%,成功通过狭窄通道的概率也比传统PRM提高68个百分点。显然,融合目标导向采样及局部节点增强的Improved PRM比传统PRM算法更适于机器人在具有狭窄通道的复杂环境中进行有效地路径规划。
4 结束语
针对具有狭窄通道的工作环境,本文提出了一种融合全局目标导向、局部节点增强的机器人Improved PRM算法。该算法中基于全局目标导向采样及随机采样的混合采样方式,可提高全局采样点落在狭窄通道内自由空间的概率,实现启发式地图增强;基于高斯分布的局部节点增强策略,可有效增强算法在狭窄空间下连通性,提高路径规划的成功率;冗余节点删除策略又可在一定程度上减少路径节点及路径代价,对算法规划的路径起到优化作用。仿真结果表明,文中所提算法在平面栅格场景下的路径规划成功率可达89.3%以上,且综合评价指数及路径质量评价指数亦高于其他算法;在六自由度机器人路径规划仿真场景下,Improved PRM算法得到的平均路径代价比传统PRM算法降低42.7%,成功通过狭窄通道概率也比传统PRM提高68个百分点。
