融合无人机光谱信息与纹理特征的棉花叶面积指数估测
2023-06-20邵亚杰汤秋香崔建平李晓娟
邵亚杰 汤秋香 崔建平 李晓娟 王 亮 林 涛
(1.新疆农业大学农学院, 乌鲁木齐 830052; 2.新疆农业科学院经济作物研究所, 乌鲁木齐 830091;3.农业农村部荒漠绿洲作物生理生态与耕作重点实验室, 乌鲁木齐 830091; 4.新疆大学机械工程学院, 乌鲁木齐 830046)
0 引言
及时准确获取作物的长势信息对提高农业生产的信息化、智能化水平具有重要的意义[1]。叶面积指数(Leaf area index,LAI)指单位土地面积上植物叶片占土地面积的倍数[2],是反映植被密度、冠层结构与功能、生物学特性与生态环境因子的重要生理指标,可作为塑造合理冠层调控措施,提高光能利用效率的重要判断依据[3]。传统的LAI测量主要包括比重法、扫描法、光电或图像法(冠层仪),只能进行小面积的人工测量[4-5],测量结果相对精准,但存在费时费力、破坏性强、监测尺度小等问题[4],难以帮助政策部门和生产部门形成有效的长势评估和农事干预。因此,在区域尺度上开发快速、无损、精确的LAI高效监测方法,对解决这一问题至关重要。
利用无人机遥感反演作物的LAI,可以避免效率低、成本高、田间操作困难等问题。该方法在农田LAI的大范围监测中被证明是有效的[5-7]。在LAI的遥感反演方法中,来自植物冠层的光谱吸收和反射特征起着关键性作用[8]。植被指数(Vegetation indexs, VIs)通过根据两个或多个波段的冠层反射率组合来突出植被的特定属性,通常在可见光和近红外范围内[9]。如:王军等[10]在大豆的LAI遥感监测中提出,与其他4个VIs相比,NDVI对大豆的反演精度较好(R2=0.74);张敏等[11]在对4个植被指数选择时发现增强型植被指数(Enhanced vegetation index, EVI),EVI得到了较高的估算结果(R2=0.64)。然而仅利用VIs进行密植作物的LAI估算时,常常存在一定的局限性。主要问题是高覆盖度的冠层结构容易限制对LAI的估算[12]。此外,VIs在作物不同生长阶段、病虫害等条件的影响下会发生变化[13-14]。而遥感影像中丰富的纹理信息(Texture features, TFs),不仅可以表征作物的冠层结构,还能够减小“同谱异物”和“同物异谱”的影响,成为有效减少作物生长后期冠层密闭以及受病虫害等因素干扰等的重要途径。因此,近年来关于融合遥感影像中的光谱和纹理特征估算作物长势的研究逐渐增多。研究表明,VIs结合TFs可显著提高生物量[15]、叶绿素含量[16]、植被覆盖度[17]等作物长势信息的估算精度。周聪等[18]、LI等[19]的研究均证实,无论是基于图像的小波能量纹理和光谱特征相结合或者是灰度共生矩阵纹理特征结合颜色指数的模型输入参数,均较单一参数类型的水稻LAI估算模型具有更高的准确性。这些研究为估算作物LAI提供了一种新的方法。然而此方法在棉花LAI的遥感监测中的应用效果还鲜有报道。
棉花是中国重要的经济作物之一,在经济发展中占据重要地位[20]。虽然前人使用无人机遥感影像在水稻、玉米和小麦等作物的LAI估算方面已有大量研究,但目前结合VIs和TFs在估算密植作物棉花LAI的应用仍较少。因此针对精准、高效获取棉花长势信息的重要性,发挥无人机灵活机动的优势,通过“点-面”结合的方式对棉花长势进行实时、宏观、快速地监测和估算,可以因地制宜制定棉花精准生产管理措施。本研究以新疆阿克苏地区棉花为研究对象,拟采用机器学习和深度学习算法,分别构建基于VIs、TFs和二者融合参数作为特征输入变量的棉花LAI估测模型,对比分析3种参数选择条件下,LAI估算精度的差异;为新疆棉田实现LAI的快速、无损、定量监测提供一种可靠的方法,为农田变量施肥、精准灌溉等精细化管理提供技术支撑。
1 材料与方法
1.1 研究区域概况
试验地点位于新疆农业科学院阿瓦提棉花科研示范基地(40°27′N,80°21′E),如图1所示,该区域属暖温带大陆性干旱气候,年平均气温10.40℃,年平均降水量46.70 mm,年平均蒸发量1 890.70 mm,无霜期211.00 d,年均日照2 679.00 h。农业生产完全依赖于灌溉。试验区土壤质地为砂壤土,田间持水率为28.92%,土壤肥力属于中等,土壤pH值为7.33。当地主要高产栽培技术为膜下滴灌技术。
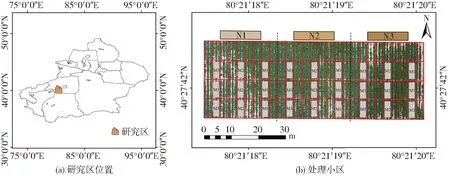
图1 研究区位置及处理小区Fig.1 Location and processing area of study area
1.2 试验设计
采用双因素裂区试验设计,以对LAI有显著影响的密度和施氮量为调节因子,以施氮量(纯氮)为主区,设置N1(0 kg/hm2)、N2(300 kg/hm2)和N3(600 kg/hm2)3个水平,密度为副区,设置M1(1.35×105株/hm2)、M2(1.80×105株/hm2)和M3(2.25×105株/hm2)3个水平;即共有9个处理,每个处理重复3次,每3幅膜划定一个小区,小区面积49 m2(长7 m,宽7 m)。
供试棉花品种为新陆中88号。采用“一膜三行三管”76 cm等行距机采棉种植模式,株距11 cm,磷肥(P2O5,150 kg/hm2)和钾肥(K2O,150 kg/hm2)全部作为基肥,在播种时一次性施入,氮肥30%作为基肥,70%作为追肥,等量分10次随水滴入。其他管理措施参照当地标准。
1.3 测定项目与方法
1.3.1地面数据获取
于蕾期(6月27日)、花期(7月23日)、铃期(8月17日)、吐絮期(9月7日)选取长势均匀的4个不同测量位点,于18:00—20:00,阳光稳定、无云时,进行LAI测量。测量采用CI-110型植物冠层数字图像分析仪(Li-Cor Inc.,美国),分别选取A、B、C、D 4个位点(图2),每个位点测量3次,取其平均值即得到各位点的平均LAI。其中位点A在中行主茎下方,位点B在中行与边行中点处,位点C在边行主茎下方处,位点D在露地中间位点处。
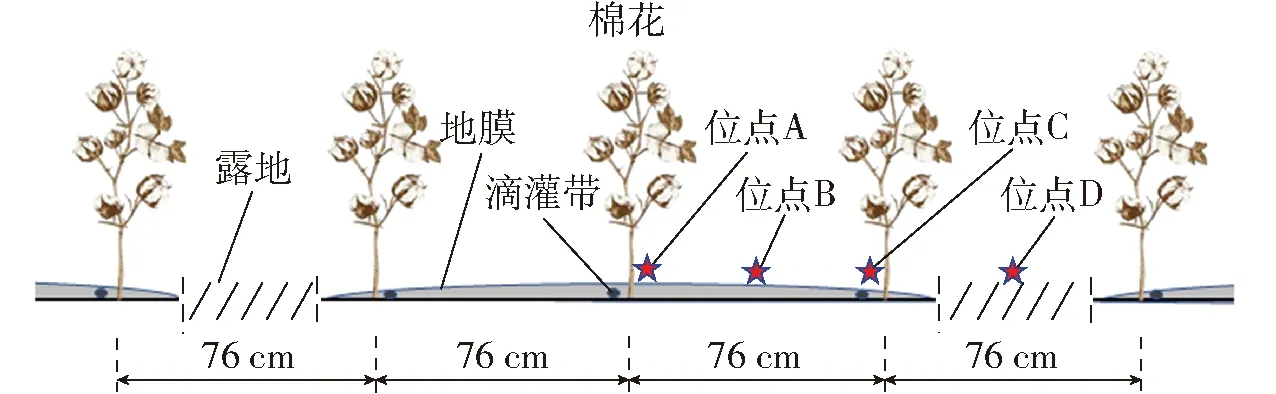
图2 棉花种植方式及LAI测量位点Fig.2 Cotton planting pattern and LAI measurement site
1.3.2无人机影像获取
获取田间LAI的当天,利用Matrice M210 RTK V2型无人机搭载多光谱相机(MicaSence RedEdge,美国)进行棉田冠层图像提取。拍摄于13:00—15:00,太阳高度角与地面近乎垂直时进行,航线设计任务高度30 m,航向重叠率75%,旁向重叠率75%,航速2 m/s,采用等间隔拍照,拍照间隔为2 m。飞行前使用多光谱传感器拍摄辐射定标版,以便后期进行影像辐射标定。
多光谱相机共有5个通道,分别为蓝、绿、红、近红外、红边波段,对应波长分别为475、560、668、840、717 nm,半高宽(FWHM)分别为20、20、10、40、10 nm,无人机影像划分示意图如图3所示。

图3 无人机影像测量位点划分示意图Fig.3 Schematic of image measurement point division by drone
1.3.3无人机数据预处理
1.3.3.1图像拼接
利用Pix4D Mapper软件对影像数据进行拼接与辐射校正。首先将原始图像数据导入软件,读取影像POS数据,设置影像相机配置信息,选择农业多光谱拼接模式,然后设定拼接过程中的匹配特征点数量和输出影像类型,生成点云和纹理信息,最后输出数字正射影像。
1.3.3.2小区裁剪
采用ArcGIS map 软件裁剪影像,先根据地面信息确定待测试验区域,建立区域shape文件在影像中勾画出试验区边界;使用裁剪工具对试验区shape进行裁剪,生成试验区域栅格数据并通过数据转换输出试验区影像数据。
1.3.3.3光谱反射率提取
使用ENVI软件对裁剪后影像提取光谱反射率。本文中选取小区反射率均值作为该小区的光谱反射率。
1.3.4植被指数与纹理特征选取
植被指数是由两个或多个波段反射率经一定方式组合而成的参数。本研究根据已有的研究成果,选取LAI监测方面效果较好的9种植被指数,计算公式如表1所示。

表1 植被指数计算公式Tab.1 Vegetation index
纹理是一种反映图像中同质现象的视觉特征,体现物体表面的具有缓慢变换或周期性变化的表面组织结构排列属性。本文使用ENVI 5.3软件进行基于二阶概率统计滤波(Co-occurrence measures)的方式来实现图像TFs的提取,对近红外波段进行提取共获取8类TFs:均值(MEA)、方差(VAR)、协同性(HOM)、对比度(CON)、相异性(DIS)、信息熵(ENT)、二阶矩(SEM)和相关性(COR)。纹理分析时选取窗口尺寸为7×7,空间相关矩阵偏移X和Y默认为1。
1.4 数据分析评价
1.4.1模型构建及反演
使用每个位点的LAI参与构建估算模型。不同VIs与地面LAI数据相关性分析后,选取相关性较高的VIs和TFs,用于棉花LAI的估算模型构建。全生育时期共获得432个LAI数据样本,由于本文的LAI实测数据需要耗费大量人工,虽然尽可能多地进行实测以保证模型训练精度,但数据集仍属于小规模样本集,因此本文按比例6∶4划分训练集和验证集。随机选取其中60%(259个样本)作为建模集,40%作为训练集(173个样本),反演LAI时选择最优估算模型对试验小区均值进行反演。
1.4.2支持向量机回归
支持向量机(Support vector regression,SVR)是在分类模型的框架下发展起来的一种被广泛使用的机器学习方法。其主要思想是将输入样本映射到高维空间,在此空间内建立了一个超平面,对所有落入此平面内的样本不计算损失,只有平面外的数据才计入损失函数,通过引入距离修正损失函数使训练样本与超平面的距离最小化,此时的超平面是拟合的函数[29]。SVR因其通用性、稳健性和有效性显示出良好的估算潜力,能够处理高维数据和非线性问题,并且具有较好的泛化能力[30-31]。本研究采用Scikit-Learn(0.21.3)包中的支持向量回归函数在Python 3.7环境中实现支持向量机算法。由于损失函数(Gamma)、误差惩罚因子C和核函数影响支持向量机的性能,参数设置中Kernel选择常用的径向基核函数(Rbf),惩罚因子C为1.0,损失函数Gamma为1/n_Features。
1.4.3偏最小二乘回归法
偏最小二乘回归法(Partial least squares regression, PLSR)是集合多元线性回归、主成分分析及相关性分析3种方法优点于一身的统计分析方法[32]。当数据集中变量较多且因变量与自变量具有多重相关性时,传统的线性回归无法精确地对因变量进行分析,从而导致构建的模型精确度较低,此时使用PLSR方法可以提高模型精度。PLSR通过依次选择正交因子来增大因变量与自变量之间的协方差,并以交叉检验的方式来确定模型中的因子数等,该方法减少了数据冗余,有利于提高计算效率。PLSR适用于多个高度共线性的变量来建立预测模型,可以有效地解决自变量之间的多重共线性问题以及数据维度较高的情况[33]。本研究采用Scikit-Learn(0.21.3)包中的偏最小二乘回归函数在Python 3.7环境中实现支持PLSR算法。本文设置主成分个数为2,其余参数按照默认使用。
1.4.4深度神经网络
神经网络是基于感知机的扩展,而深度神经网络(Deep neural network,DNN)可以理解为有很多个隐藏层的神经网络。DNN内部的神经网络层可以分为3类:输入层、隐藏层和输出层,通过堆叠多个隐藏层来达到提取更高阶的特征信息,这些信息在回归预测中有助于提高性能[34]。DNN模型现已成为解决各种分类和回归问题的方法[34-36]。本文设计的网络结构包含输入层、隐藏层和输出层,结构中层与层直接全连接,同层之间的神经元不连接。DNN共分为4层:1个输入层、2个隐藏层和1个输出层。将图像中提取的植被指数、纹理特征和纹理指数转换为与每个测量点LAI相对应的一维向量,以此作为输入层,输入层设置为3个神经元,隐藏层的每层神经元个数依次是6、4,输出层设置为1个神经元,并以最终输出结果来估算LAI。在DNN模型中选取ReLU作为激活函数,使用均方根误差作为优化函数,选择均方误差作为损失函数,迭代100次。本研究采用Python 3.7基于Keras 2.3.0框架搭建了此网络结构。
1.4.5模型验证
选取决定系数(Coefficient of determination,R2)、均方根误差(Root mean square error,RMSE)和相对均方根误差(Relative root mean square error, RRMSE)作为评价估算模型的指标[36]。估算模型和验证模型的R2越大,RMSE和RRMSE越小,表明模型稳定性越好,预测精度越高。
2 结果分析
2.1 叶面积指数与光谱数据分析
棉花各生育时期实测棉花LAI结果如表2所示,随着棉花生长,不同密度与施氮量处理下棉花LAI总体呈现先增大后缓慢降低的趋势。每个时期获得108 个样本,生育期累计获得432 个样本。LAI平均值由蕾期(1.82)增加至花期(2.81)后,在铃期、吐絮期逐渐下降,吐絮期平均值为1.85。各生育时期标准差为0.21~0.27,方差在0.04~0.07之间,变异系数在0.08~0.12之间。结果表明,标准差、方差、变异系数较小,说明LAI的离散程度小,即LAI分布均匀。
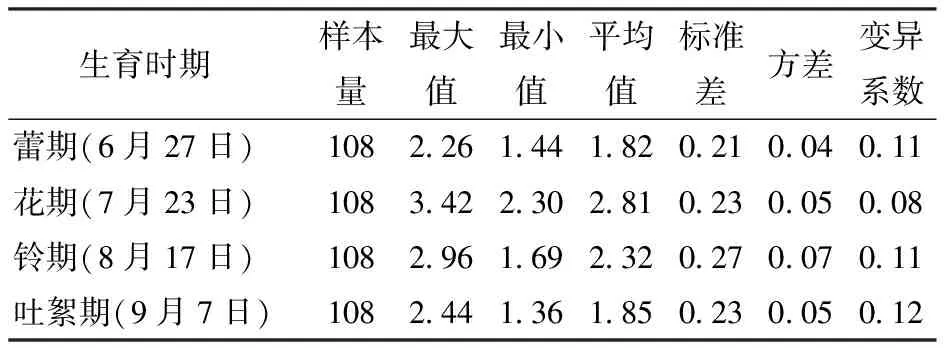
表2 棉花叶面积指数数据统计Tab.2 Cotton leaf area index data statistics
2.2 基于植被指数的棉花LAI估算模型
VIs与LAI相关性分析结果如图4所示。结果表明,VIs与LAI均呈现显著正相关,且相关系数为0.747~0.830。在所选的VIs中VI(nir/red)与VI(nir/green)相关性较高,分别为0.822、0.830。图4表明随着LAI的增加,VIs增加,但在LAI大于2.0时,NDVI、GNDVI、SAVI、OSAVI和MSAVI的增长幅度减小。
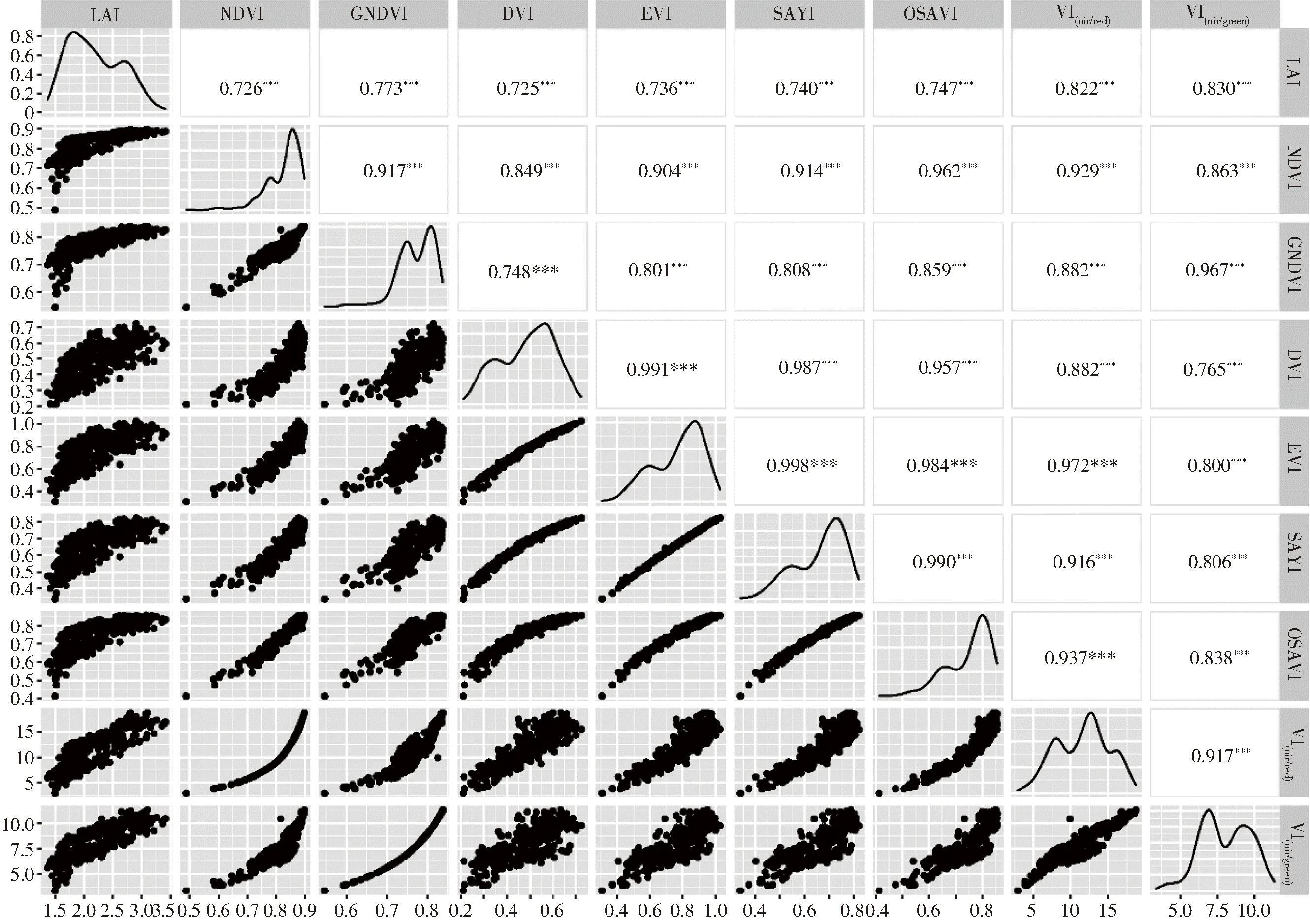
图4 LAI与植被指数相关性分析Fig.4 Correlation analysis between LAI and spectral parameters
由于VIs与LAI之间均存在显著相关性,为避免数据产生大量冗余,因此引入相关系数绝对值|r|最高的4个植被指数(VI(nir/green)、VI(nir/red)、GNDVI、OSAVI)作为自变量,以LAI为因变量,构建了SVR、PLSR和DNN的LAI估算模型。同时,通过比较模型估计值与实测值来验证模型的估算精度(R2、RMSE、RRMSE),如表3所示,3种建模算法的估算精度为0.72~0.78,PLSR模型具有最低的估算精度(建模集R2=0.72,验证集R2=0.68),而DNN模型具有最高的估算精度(建模集R2=0.78,验证集R2=0.71),表明DNN模型的估算精度最好。
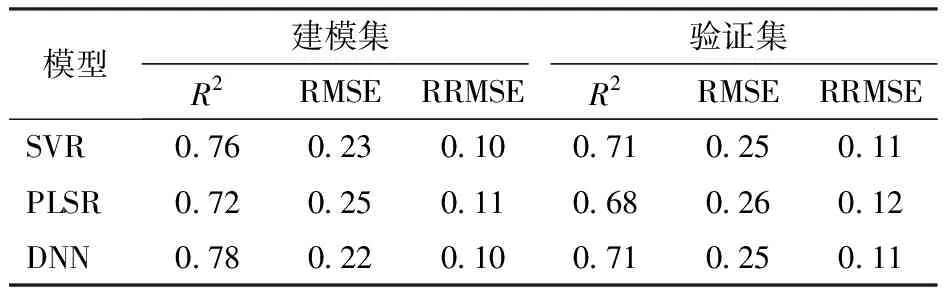
表3 基于植被指数的棉花LAI估算结果评价Tab.3 Evaluation of LAI estimation results of cotton based on vegetation index
2.3 基于纹理特征的棉花LAI估算模型
图5表明LAI与近红外波段反射率相关性最佳,因此本文选择该波段提取TFs,并筛选出与LAI相关系数绝对值|r|最高的MEA、HOM、ENT和SEM作为自变量,构建了基于SVR、PLSR和DNN算法的LAI估算模型。在模型变量的选择方面,使用TFs变量构建的LAI估算模型精度低于VIs,在模型算法方面,3种建模算法的精度为0.51~0.62(表4),其中PLSR的精度最低(建模集R2=0.51,验证集R2=0.49),SVR精度最高(建模集和验证集的R2分别为0.62、0.58)。
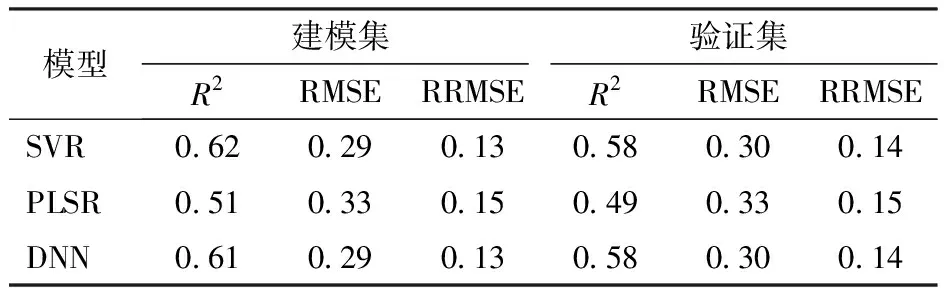
表4 基于纹理特征的棉花LAI估算结果评价Tab.4 Evaluation of LAI estimation results for cotton based on texture features
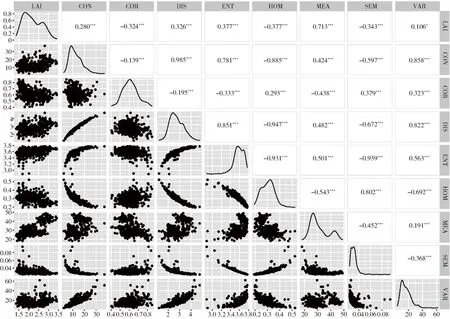
图5 LAI与纹理特征相关性分析Fig.5 Correlation analysis between LAI and textural characteristics
2.4 基于结合植被指数和纹理特征的LAI估算模型
本文依据相关系数绝对值|r|来筛选VIs和TFs的最佳组合为VI(nir/red)、VI(nir/green)、HOM和MEA,表5反映了基于SVR、PLSR和DNN算法构建LAI估算模型的结果。相比之下,SVR算法具有最高的估算精度(建模集:R2=0.82,RMSE为0.20,RRMSE为0.09;验证集:R2=0.78,RMSE为0.22,RRMSE为0.10)。VIs和TFs组合构建LAI的SVR估算模型比VIs、TFs估算的模型精度分别提高7.89%、32.26%。
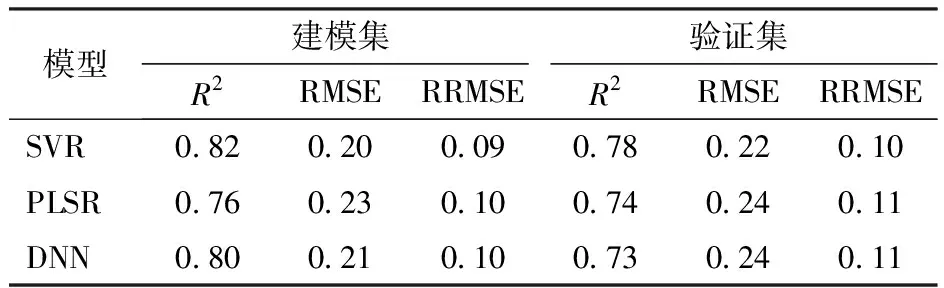
表5 基于植被指数和纹理特征结合的棉花 LAI估算结果评价Tab.5 Evaluation of cotton LAI estimation results based on combination of vegetation index and texture features
本研究中LAI最优估算模型为SVR模型,基于此模型对棉花4个生育时期LAI进行反演,最终得到棉花各生育期的LAI空间分布图(图6)。结果表明,棉花LAI随着生育期的推进呈现先增加后减小的趋势,在花期达到最大值。蕾期反演的LAI在1.54~1.97之间,N2M3处理下的LAI达到最大值;花期反演的LAI在2.15~2.86之间,同样为N2M3处理的LAI达到最大值;铃期反演的LAI在2.11~2.34之间,N3M2处理下的LAI达到最大值;吐絮期反演的LAI在1.60~2.03之间,在N1M3处理下LAI达到最大值。在空间分布上,棉花叶面积指数因不同的施氮量和密度处理具有明显差异,LAI较好的处理为N2M3处理。
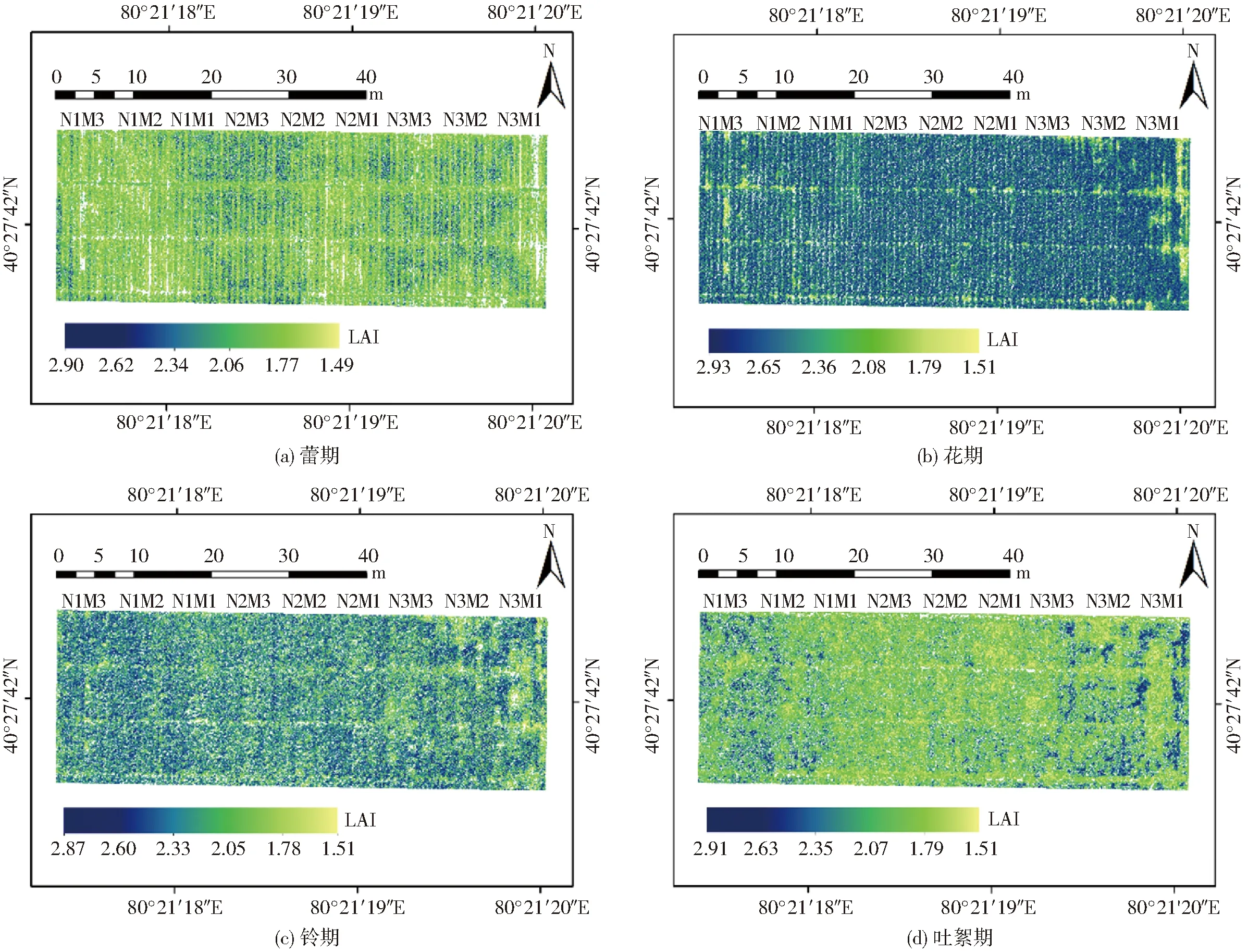
图6 棉花不同生育期LAI时空分布图Fig.6 Spatial and temporal distributions of LAI in different growth stages of cotton
3 讨论
无人机是一种新型遥感数据获取平台,具有分辨率高、作业效率高的优点,在农业领域监测作物长势信息等方面具有重要作用。多光谱传感器可以获取遥感所需的红、绿、蓝、红边和近红外5个重要波段的数据,相较于RGB三通道数码相机和高光谱传感器,无人机搭载多光谱传感器具有成本低、数据处理简单等特点,应用于农业遥感领域具有一定的优势。有学者研究利用无人机搭载多光谱传感器组成的低空遥感平台,对冬小麦LAI[37]、大豆LAI[38]的反演研究结果表明,利用无人机多光谱影像对作物LAI进行估算是可行的。本研究通过无人机搭载多光谱传感器采集棉田遥感影像对棉花LAI进行估算。本研究基于VIs和TFs构建不同算法的棉花LAI反演模型,结果证明了基于无人机多光谱影像估算棉花LAI的可行性。
3.1 估算模型变量的选择影响因素
在模型变量的选择方面,根据VIs与TFs对棉花LAI的敏感程度,选择相关性较高的变量,可以有效提高反演模型精度。本研究基于LAI与VIs和TFs的相关性来选择模型变量,综合利用棉花生长季内多生育时期光谱信息对棉花LAI进行估算。此方法相较于单一生育时期进行估算LAI更加科学合理,能够有效提高LAI的估算精度。王修信等[39]对林地LAI的估算方法研究表明,利用多光谱植被指数NDVI、RSR、SAVI构建的估算模型精度最高,R2达到0.83,RMSE为0.19。王亚杰[40]以EVI、OSAVI、SAVI、NDVI、RDVI构建了玉米LAI反演模型,R2为0.91。本文选取相关性较高的VI(nir/green)、VI(nir/red)、GNDVI和OSAVI构建估算模型,基于VIs的DNN估算模型的估算精度R2为0.78,RMSE为0.22,RRMSE为0.10。对于不同研究区、使用不同的建模方法、不同的VIs得到的模型,虽然基本具有较好的估算结果,但在精度上会有一定的差异。在传统的统计分析中通常选用单一VIs进行构建LAI估算模型,但单一VIs所包含的信息比较片面且存在不同程度的饱和性[41]。纹理能表征物体表面的内在特性,同时TFs提供了更多的植被冠层结构信息,可以提高LAI的估算精度。因此,将更多的光谱信息作为变量以构建估算模型十分重要。本文研究发现在仅使用TFs对棉花LAI估算时,估算精度小于VIs估算模型。而在估算LAI时加入TFs有利于提升模型的准确性,结合VIs和TFs构建的SVR估算模型的验证集R2分别提高9.86%、34.48%。为以后估算作物的LAI研究提供了新的思路。本研究已经证明了采用加入TFs来估算棉花LAI的方式能够有效提高估算精度,但是否存在更好的估算方式还有待研究。其次,本研究使用的是皮尔逊相关系数的方法来确定模型构建时的输入参数,而且在选择VIs和TFs中仅选择了相关系数绝对值|r|最高的4个进行建模与评价,而对于其他的特征参数筛选方法还需要进一步研究。
3.2 不同估算模型对LAI估算精度的影响
建模算法的选择对于估算作物长势信息的估测精度影响较大。目前利用无人机多光谱影像进行植物生长参数的估算研究,主要通过光谱参数与实测值建立经验统计或机器学习模型进行估测。牛庆林等[42]基于无人机影像数据监测玉米LAI,使用逐步回归分析方法建立估算模型,R2为0.63,RMSE为0.40。而传统的线性回归方法对模型的估算精度往往不高,而机器学习以独特的优势逐渐替代了传统逐步回归,在作物长势监测中得到了广泛应用[43]。王瑛等[44]基于六旋翼无人机获取小麦冠层多光谱影像,结果发现SVR构建小麦LAI估算模型效果最佳,R2达到0.83,RMSE为0.29。而本研究则是构建了1种深度学习估算模型和2种机器学习模型,DNN模型通过加入多个隐藏层,使用Sigmoid和ReLU等非线性激活函数,使得DNN模型能够挖掘出数据之间的复杂关系,从而实现模型估算性能的提高。本文通过选取不同的参数组合方式进行建模,有助于发挥DNN模型的特征融合优势。SVR模型能够将数据映射至高维特征空间,在高维特征空间上建立一个超优平面决策边界,从而进行样本分类,SVR克服了传统线性回归方法的不足,在解决本研究中小样本和非线性问题时具有独特优势[45]。PLSR是结合了PCA、MLR和CCA 3种分析方法的优势,在单因变量和多个自变量的回归分析中,该方法简单稳定且精度较高[46]。因此本文选择这3种方法建立棉花LAI的估算模型。3种算法在不同参数组合建模的方式中,估算精度由大到小均呈现为VIs和TFs融合模型、VIs模型、TFs模型。在仅使用VIs构建估算模型时,深度学习DNN模型的估算精度最高,而基于VIs和TFs融合构建时使用SVR估算模型效果最佳,R2为0.82,RMSE为0.20,证明将SVR算法用于构建VIs和TFs结合的棉花LAI估算模型具有较好的应用前景。本研究得出SVR模型优于DNN模型和PSLR模型,SVR模型和DNN模型差距较小,原因可能是PLSR模型主要用于处理多元线性回归问题,而SVR和DNN则能够处理非线性问题。DNN模型的特点是能够捕捉复杂的数据特征,SVR模型的特点则是可以处理高维数据,本研究使用全生育期的数据进行构建估算模型,包含了多个特征和多个时刻的测量值,这个多维数据集可能提高了SVR模型的估算能力。虽然使用SVR和DNN模型估算棉花LAI具有较好的结果,但后续研究中也可以尝试更多的模型构建算法。
4 结束语
本研究利用无人机搭载多光谱传感器获取多生育时期棉花冠层光谱影像,通过分析光谱指数和纹理信息与LAI的定量关系,选择VIs、TFs和二者融合的方式,运用SVR、PLSR和DNN构建棉花LAI估算模型,VI(nir/green)、VI(nir/red)、GNDVI、OSAVI、MEA与LAI具有较高的相关性;采用SVR建立的LAI估测精度最高(R2=0.78,RMSE为0.22,RRMSE为0.10);在3种估算模型中,植被指数与纹理特征相结合的SVR模型较VIs、TFs模型精度分别提高7.89%和32.26%。
