基于预瞄PID的自动泊车路径跟踪分析
2023-06-20熊胜健隋立洋鲁若宇
骆 嫚,熊胜健,隋立洋,鲁若宇,江 辉*
基于预瞄PID的自动泊车路径跟踪分析
骆 嫚1,熊胜健1,隋立洋2,鲁若宇1,江 辉*1
(1.东风悦享科技有限公司,湖北 武汉 430058;2.武汉理工大学汽车工程学院,湖北 武汉 430070)
为减少路径跟踪的误差,文章设计了基于预瞄误差的比例-积分-微分(PID)控制器。首先,采用直线-圆弧-回旋曲线拼接的方法生成了垂直泊车场景下曲率连续的全局路径。其次,设计了预瞄点、参考点及预瞄误差的计算方法,并将预瞄误差作为PID的输入以设计路径跟踪控制器。最后,通过Simulink/CarSim联合仿真对预瞄PID算法进行了验证,仿真及试验的结果表明,文章所提出的基于预瞄PID的路径跟踪算法虽然原理简单,但是跟踪精度较高,可以满足自动泊车的需求。
自动泊车;垂直泊车;路径跟踪;预瞄误差;PID;Simulink/CarSim
自动泊车系统(Automated Parking System, APS)作为高级辅助驾驶系统(Advanced Driving Assistance System, ADAS)的重要组成部分,成了目前研究的热点。当驾驶员将车辆开到车位附近并开启APS功能后,系统通过环视相机及超声波雷达对车位进行检测及定位,根据自车位置相对车位的位姿规划出一条入库的全局路径,路径跟踪模块根据规划下发的全局路径及自车实时位置实时计算方向盘转角,控制车辆精准泊车入库。路径跟踪模块是自动泊车的关键技术,提高跟踪的精度可避免车辆在泊车入库过程中与周边车位剐蹭。
国内外针对泊车路径跟踪技术的研究有很多,主要使用的算法有比例-积分-微分(Proporti- onal Integral Derivative, PID)控制、滑膜控制、模糊控制、线性二次型调节器(Linear Quadratic Regulator, LQR)和模型预测控制(Model Predictive Control, MPC)等[1-8]。文献[1]提出基于前馈+PID反馈的横向控制模型,相比纯PID控制提高了路径跟踪精度。文献[2-4]基于终端滑模理论推导了非时间参考的泊车路径跟踪滑膜控制律,提高了泊车路径跟踪控制的鲁棒性。文献[5]采用模糊控制的方法对车辆路径进行跟踪控制。基于模糊控制的路径跟踪控制方法是根据驾驶员及专家知识经验,选取合适的隶属度函数和模糊逻辑以及变量值作为模糊控制器的输入量和输出量。文献[6]设计了LQR反馈控制器来解决泊车路径跟踪问题,选择改进的遗传算法对LQR控制器的加权矩阵对角参数进行优化,文献[7]和文献[8]分别采用线性和非线性的模型预测控制模型进行自动泊车的路径跟踪,非线性的方法相比线性的方法跟踪精度更高,但是算法的实时性有所下降。
城市中的垂直车位较为常见,以直线-圆弧-回旋曲线生成垂直车位的全局路径,作为路径跟踪算法的输入对路径跟踪算法进行验证。本文提出以预瞄点的误差作为PID控制器的输入,实时纠正车辆在入库过程中的误差,在保证实时性的前提下提高了路径跟踪的精度。
1 垂直泊车路径规划方法
基于直线-圆弧规划的几何法是自动泊车常用的路径规划算法,其原理简单、算法复杂度低、实时性好。但是在直线和圆弧连接处存在曲率不连续的情况,提高了路径跟踪算法的跟踪难度,为减少因路径规划带来的不利影响,本文采取回旋曲线对曲率进行优化,以生成曲率连续的泊车全局路径。
1.1 基于直线-圆弧法的垂直泊车路径规划
基于直线-圆弧法的垂直泊车路径规划方法有一段式、两段式和三段式等。一段式方法较为简单,可一次性倒车入库,但其对行车通道的宽度有一定要求,若行车通道宽度较窄或车辆起始位置距离车位上边沿的横向距离较近,则无法通过一段式的方法入库。本文假设行车通道宽度满足要求,以一段式的方法进行垂直泊车的路径规划。
首先,对泊车的局部地图进行建模。如图1所示,以车位左下角1为坐标原点建立坐标系111。图1中,为道路宽度;为车位长度;为车位宽度;1、2、3分别为安全距离要求,人为设置但需大于等于0;为车辆在泊车转向起始点距离车位上边界的距离。结合车辆自身参数和以上参数可计算得出一段式泊车入库的三个关键点:倒车转向起始点1、泊车入库时车身与库位平行的点2和泊车过程的终点3。
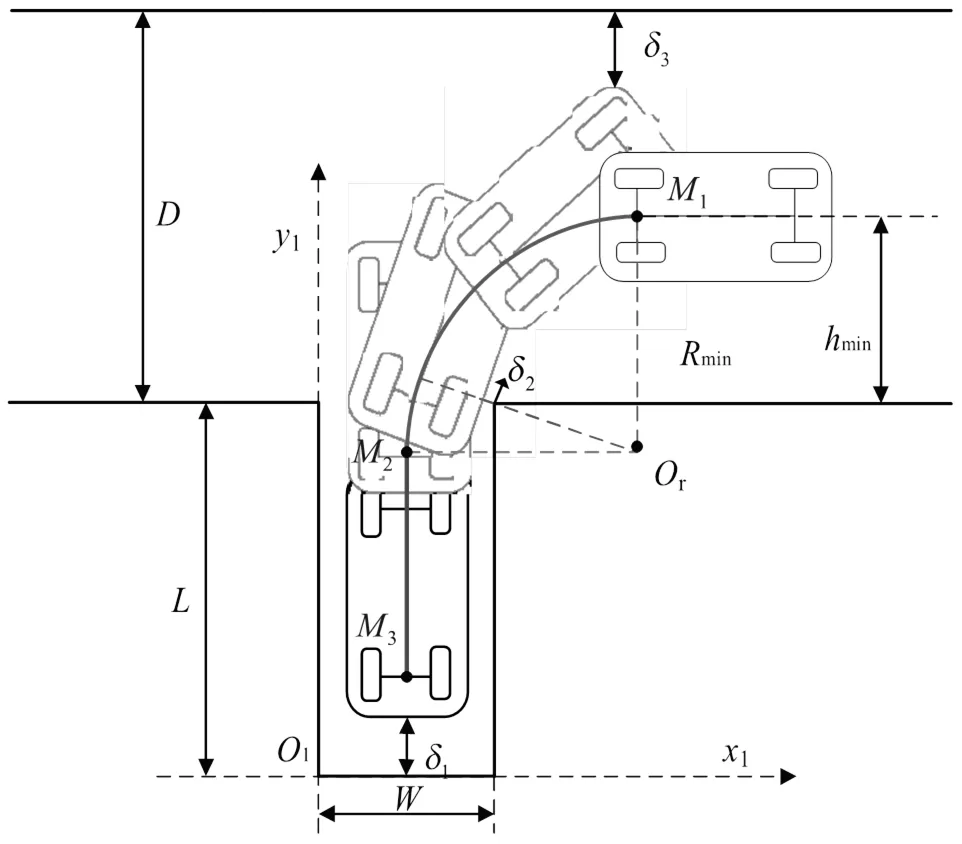
图1 泊车过程建模示意图
泊车过程中存在碰撞风险的点主要有三个,分别为车辆下边界与车位下边界、车位右上角与车身右轮廓、车辆左前角与行车通道上边界,这三个碰撞点分别与1、2、3有关。停车场的宽度通常在6 m左右,车辆左前角与行车通道上边界发生碰撞的概率比较低,而通过设置1可有效地控制车辆不与车位下边界发生碰撞,故需要重点分析车位右上角的碰撞风险,该点的碰撞风险与和2有关,越小则该点的碰撞风险越大。设该点不发生碰撞的最小值为min,参考文献[9],可计算出以一段式入库min的表达式:
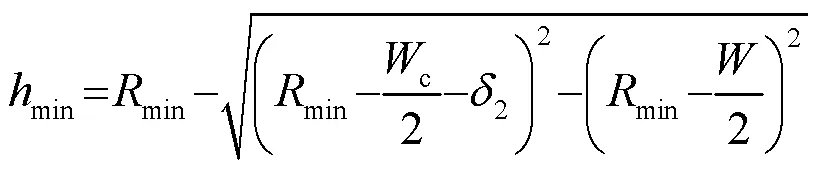
当

设1、2、3的坐标分别为(x1,y1)、(x2,y2)、(x3,y3),则三点的具体坐标表达式如下:
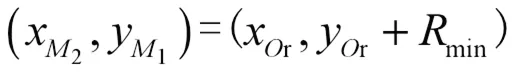


1.2 基于回旋曲线的优化
基于直线-圆弧的泊车路径规划方法较为简单,但是实际中若想要跟踪这条路径,车辆需要在1处停车,将方向盘右打满后开始倒车,在2点处停车,回正方向盘后再倒车。这不符合驾驶员的倒车习惯,会增加泊车的时间,且原地转向会加剧轮胎的磨损,故需要优化。该问题的根本在于直线的曲率为0,圆弧的曲率为1/min,路径在直线和圆弧拼接处的曲率不连续。因此,本文提出基于回旋线拼接圆弧的方法,在图1的1点附近加入一段回旋曲线使曲率由0缓慢增加至1/min,在2点附近加入一段回旋曲线使曲率由1/min缓慢下降至0,以解决泊车路径曲率不连续的问题。
回旋曲线是曲率随着曲线长度线性增加的一类曲线。设曲率变化率为,其表达式如下:
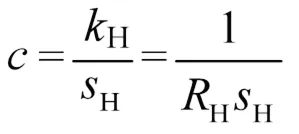

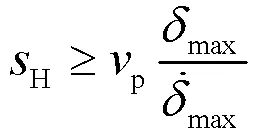
式中,p为泊车过程的最高车速,一般≤1 m/s;max为前轮最大转角,根据实车数据,max=30°;max为前轮转角最大变化率,经实测,取max=30 °/s;H的值越大,回旋曲线曲率变化越缓慢,根据以上分析,取H=1.5 m。
根据下式可计算回旋曲线的散点位姿,其中、分别为横纵坐标,为航向角。

参考文献[3]使用回旋曲线对直线-圆弧的连接处M1点和M2点进行拼接,以生成曲率连续的全局参考路径。经回旋曲线优化后车辆的路径如图2所示,可以看出,泊车全局路径缓慢连续变化。
2 基于预瞄PID的泊车横向控制算法
规划模块下发车辆在泊车坐标系的全局参考路径后,定位模块可给出车辆在泊车坐标系的实际位置,根据全局路径和实时位姿可计算出车辆的横向误差,横向跟踪模块需实时调整方向盘转角的输出来纠正横向误差,使智能车精准地沿全局参考路径行驶。以车辆的后轴中心点处的横向误差作为PID的输入进行反馈控制具有一定的滞后性,本文采用一定的预瞄距离计算预瞄点,以预瞄点向全局路径做投影,找到相应的参考点并计算预瞄点的横向误差,以预瞄点的横向误差作为预瞄误差,并采用PID控制器对预瞄误差进行实时反馈修正。
2.1 预瞄点选取
图3中111为泊车坐标系,为车辆后轴中心坐标系,车辆后轴中心点的位置为(,),为汽车朝向与轴的夹角,可由定位模块直接给出。(prepre)为预瞄点的坐标,(rr)为参考点的坐标,pre为从后轴中心出发沿汽车行驶方向的预瞄距离,倒车时pre取负值,pre为预瞄误差,因泊车速度较低,故预瞄距离采用固定值,通过仿真试验调整而得。
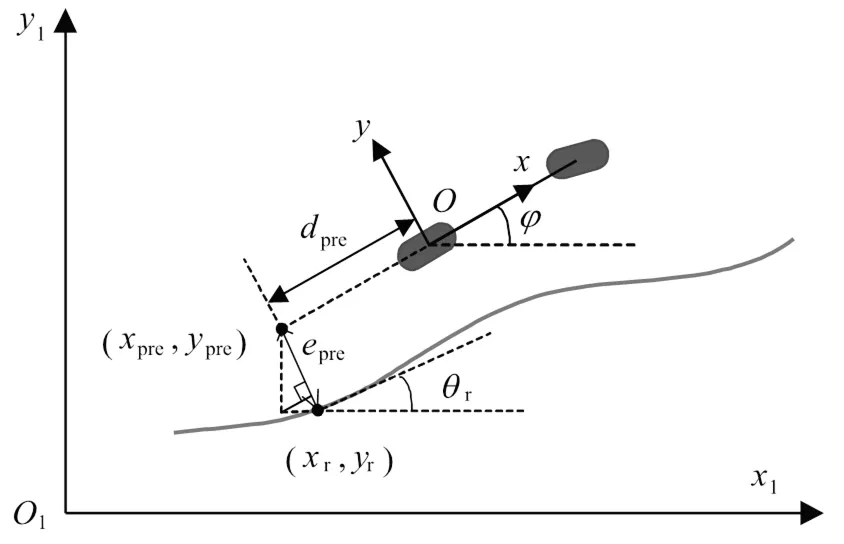
图3 预瞄点选择示意图
预瞄点可由下式计算:
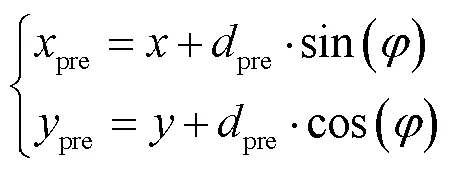
2.2 参考点选择
全局参考路径是如图4所示的离散点,已知汽车当前位置的预瞄点0,需在离散点中找到当前位置的参考点ref。遍历离散点可找到最近匹配点m当离散点很稠密时,m可等效为ref,但是当离散点稀疏时,m0与m点的切线方向不垂直,导致计算出的横向误差存在偏差。为解决该问题,取m前后两个离散点1、2,设过1、2的直线斜率为l,1、2点的坐标分别为(x1,y1)、(x2,y2),则l的表达如下:
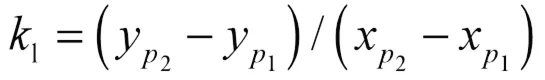
设参考点r的坐标为(rr),则r和r的表达如下:

除此之外,预瞄误差的计算还需要参考点的航向角r。分别用12表示点2、r距离点1的距离。
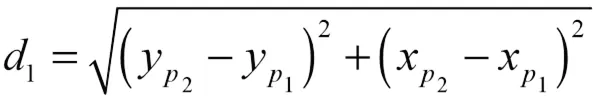
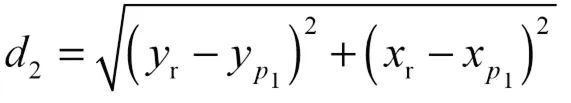
令221,以1和2分别表示点1、2的航向角,则r的表达如下:
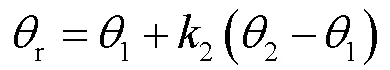
2.3 基于预瞄误差的PID横向控制模型
得到预瞄点和参考点后,计算两点之间的距离可得到预瞄点的横向误差,但这样无法区分正负,故采用如下式来求预瞄误差:
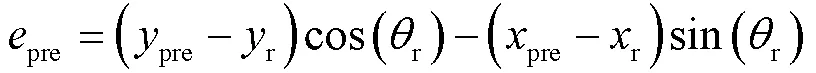
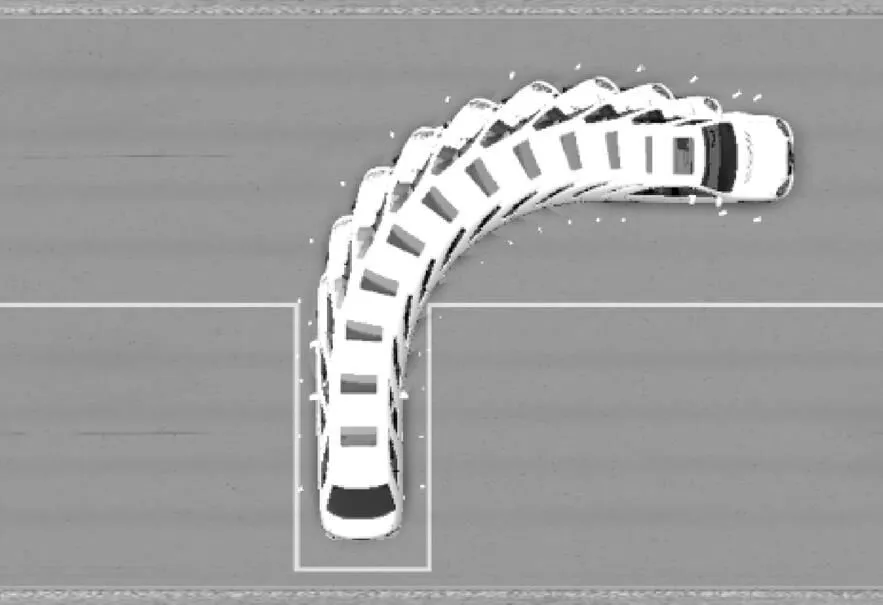
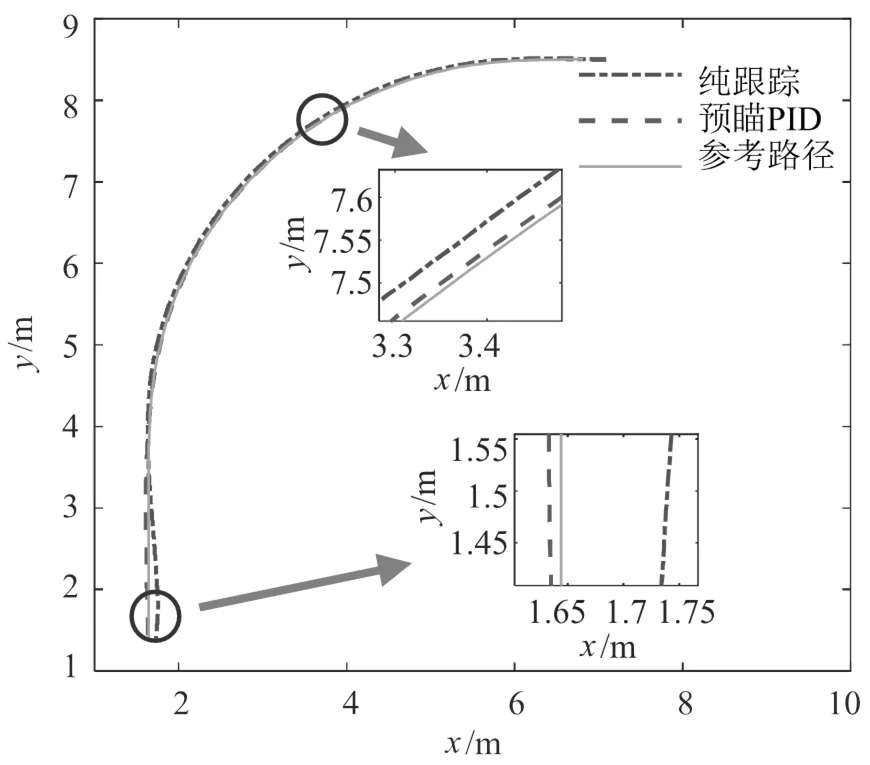
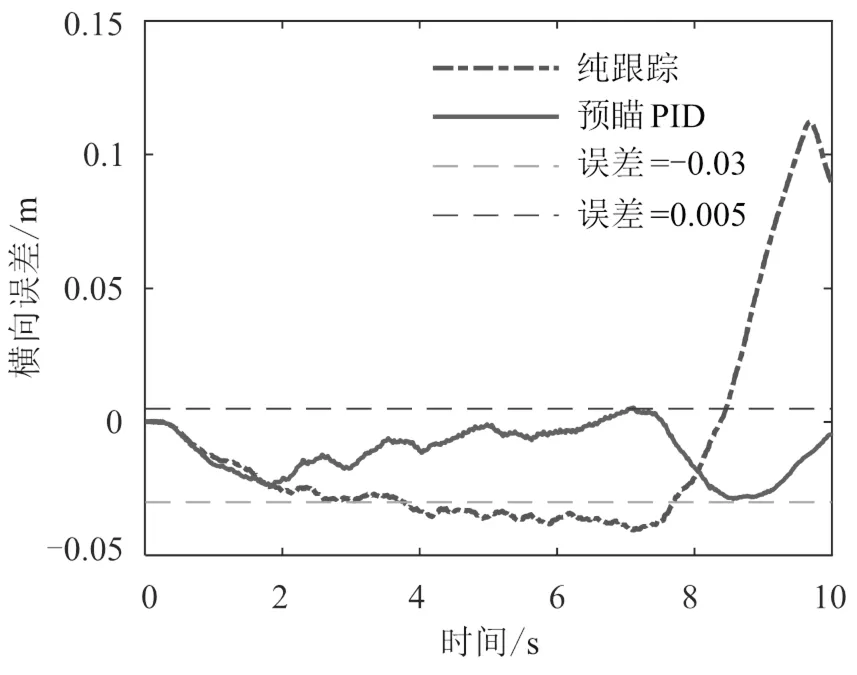
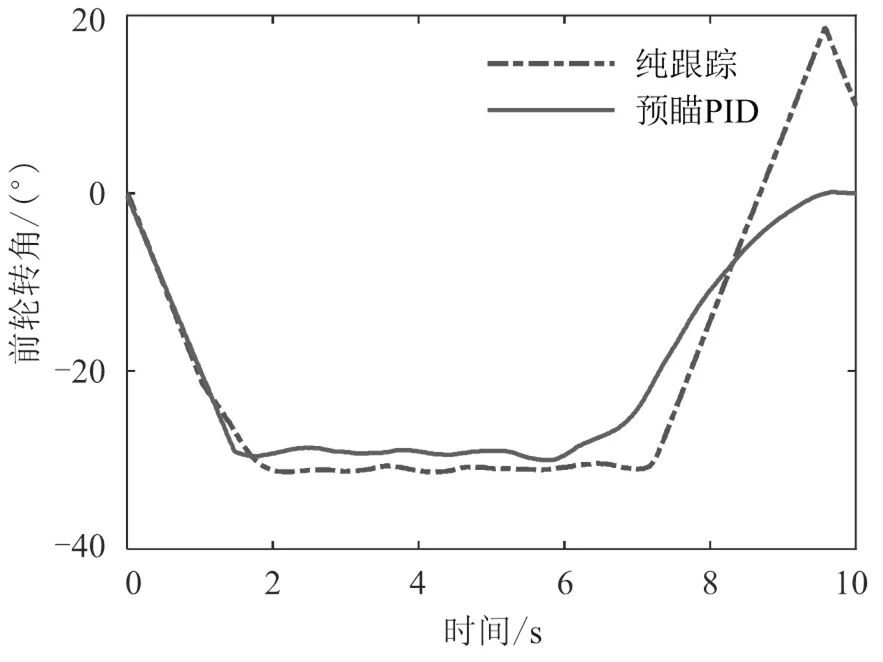
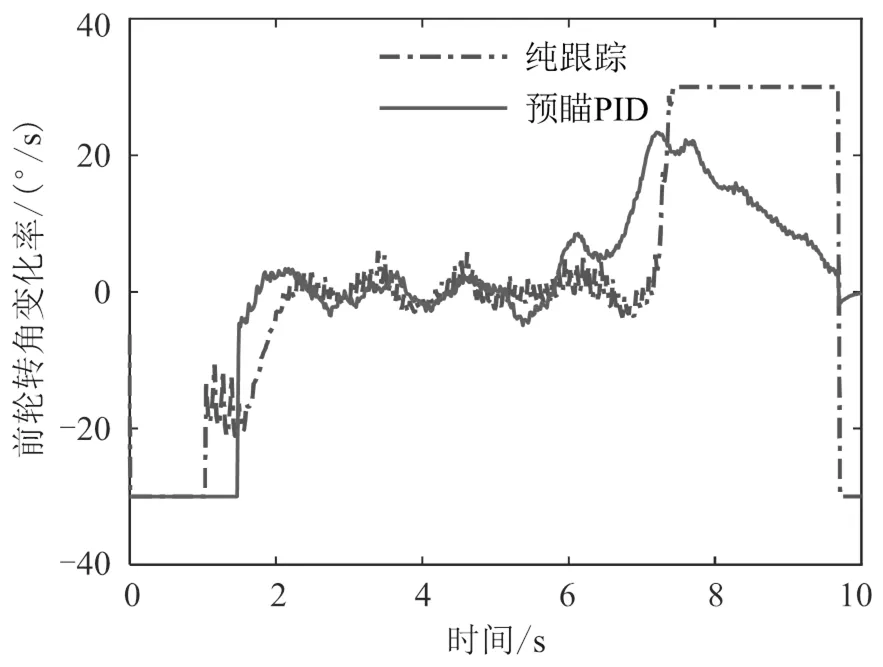
以预瞄误差作为PID控制的输入,前轮转角作为输出,参考PID模型表达式,可建立基于预瞄PID的泊车横向控制模型。前轮转角输出值需满足 使用CarSim和Simulink进行仿真时可直接控制车辆的左右前轮转角,前辆等效前轮转角与左右前轮转角需满足阿克曼转向关系,如式(17)、式(18)所示,以保证车辆在转弯时内外轮的轨迹接近同心圆,避免轮胎过度磨损。 式中,l、f分别为左、右前轮的转角;a为车辆前轮的轮距;为车辆的轴距。 进行实车控制时,控制量为方向盘转角,方向盘转角与前轮转角之间可参考下式进行换算。 式中,为转向系的传动比,可通过车辆出厂时的试验标定得到;s为方向盘转角。 基于CarSim和Simulink进行泊车横向控制的联合仿真,车辆及车位的参数如表1所示。在CarSim中搭建泊车的场景及车辆动力学模型,在Simulink中搭建横向控制模型,泊车路径由MATLAB的工作空间导入。泊车横向控制器的输出为车辆的左、右前轮转角,输入后轴中心点实时位置、航向角及参考路径。CarSim车辆模型输出的位置为车辆前轴中心点的坐标,故需结合轴距、实时航向角计算车辆后轴中心点的位置。车辆及车位的参数如表1所示。 表1 车辆参数表 参数符号定义取值 Wc车辆宽度/mm1 600 Wa前轮距离/mm1 415 lf前轴与车辆前端的距离/mm1 200 lr后轴与车辆后端的距离/mm1 200 l前后轴之间的距离/mm2 600 LcWWcWcδmaxi车辆长度/mm车位宽度/mm车位长度mm/行车通道宽度/mm最大前轮转角/(°)转向系传动比/mm5 0002 6005 5006 0003016.8 CarSim可以回放车辆仿真过程的实时动画及车辆运动的拖影图,泊车过程的车辆轮廓图如图5所示,可以看出车辆可以平稳且无碰撞地泊车入库。 图5 泊车过程车辆拖影图 本文与同样基于预瞄距离进行控制的纯跟踪算法进行了对比,从横向误差和航向误差两个角度分析两个算法的跟踪精度。纯跟踪算法的原始输出存在抖动,本文对其控制量采用一阶滤波算法进行平滑处理,控制量的平滑度及路径跟踪的精度都有较大的提升。预瞄PID和纯跟踪算法的实际路径与参考路径地对比如图6所示。可以看出两个算法在圆弧倒车阶段的路径跟踪效果比较好,但在车辆与库位接近平行的直线倒车阶段,纯跟踪算法误差较大,实际路径表现为轻微的曲线。在泊车的终点位置,预瞄PID的跟踪误差更小,预瞄PID和纯跟踪算法的横向误差分别为-0.01 m和0.08 m。 图6 实际行驶路径与参考路径对比图 图7 横向误差对比图 图8 航向误差对比图 图7和图8展示了两种算法在泊车过程中的横向误差和航向误差,在横向误差方面,预瞄PID的横向误差在−0.03~0.005 m,纯跟踪算法的横向误差在−0.05~0.1 m,预瞄PID在横向误差上的表现要优于纯跟踪算法。在航向误差方面,预瞄PID的航向误差在−0.8~4.5°,终点位置的航向误差为0.9°;纯跟踪算法的航向误差在−1.1~4°,终点位置的航向误差为−1.1°,两者相差不大。 图9和图10分别展示了两种算法前轮转角的输出及前轮转角的变化率。在刚开倒车阶段,预瞄PID算法几乎以最大的前轮转角变化率增大前轮转角,前轮转角以很快的速度收敛到接近最大值,在方向盘回正阶段,预瞄PID算法比纯跟踪在更早的时刻便开始回正,且回正后前轮转角没有出现振荡。而纯跟踪算法回正的时间较为滞后,以此造成回正过程的横向误差较大,需要以较大的前轮转角变化率来回正,故回正后的直线阶段控制量超调,实际路径出现曲线。 图9 前轮转角输出对比图 图10 前轮转角变化率对比图 采用回旋曲线-直线-圆弧拼接的方法生成了垂直车位下曲率连续变化的泊车路径,针对自动泊车场景车速低、路径曲率大等特点设计了基于预瞄误差的PID路径跟踪控制器,最后通过CarSim和Simulink联合仿真,验证了路径跟踪控制器的有效性。 通过对仿真结果的分析,可得出结论:以预瞄PID算法进行自动泊车的路径跟踪控制,可得到较好的跟踪效果。该算法相比其他路径跟踪控制算法具有一定优越性,其相比于纯跟踪等其他不基于动力学模型的算法,跟踪精度更高,相比于MPC等基于动力学模型的算法,其算法简单、实时性好、对控制器算力要求更低。 [1] 杜文豪.自动平行泊车的路径规划及其跟踪控制研究[D].重庆:重庆大学,2019. [2] 张家旭,王晨,赵健,等.面向狭小平行泊车位的路径规划与跟踪控制[J].吉林大学学报(工学版),2021,51 (5):1879-1886. [3] 张家旭,赵健,施正堂,等.基于回旋曲线的垂直泊车轨迹规划与跟踪控制[J].东南大学学报(自然科学版),2020,50(1):182-191. [4] 张家旭,赵健,施正堂,等.基于回旋曲线的平行泊车路径规划和跟踪控制[J].吉林大学学报(工学版), 2020,50(6):2247-2257. [5] 尤田田.自动泊车路径规划及跟踪控制方法研究[D].合肥:合肥工业大学,2021. [6] 卢庆志.基于遗传算法的自动泊车路径规划及跟踪控制研究[D].西安:长安大学,2020. [7] 胡远志,何朋声,刘西.基于模型预测控制的平行泊车控制方法[J].重庆理工大学学报(自然科学),2020,34 (10):1-8. [8] 顾青,白国星,孟宇,等.基于非线性模型预测控制的自动泊车路径跟踪[J].工程科学学报,2019,41(7): 947-954. [9] 孙思.自动垂直泊车系统转向控制策略的研究[D].北京:清华大学,2015. Analysis of Automatic Parking Path Tracking Based on Preview PID LUO Man1, XIONG Shengjian1, SUI Liyang2, LU Ruoyu1, JIANG Hui*1 ( 1.Dongfeng Yuexiang Technology Company Limited, Wuhan 430058, China;2.College of Automotive Engineering, Wuhan University of Technology, Wuhan 430070, China ) In order to reduce the error of path tracking, a proportional integral derivative (PID) controller based on preview error is designed. Firstly, a global path with continuous curvature in vertical parking scenarios is generated by splicing line-arc-cyclotron curves. Secondly, the calculation method of preview point, reference point and preview error is designed, and the preview error is used as the input of PID to design the path tracking controller. Finally, the preview PID algorithm is verified by Simulink/CarSim co-simulation. The simulation and test results show that the path tracking algorithm based on preview PID proposed in this paper is simple in principle, but has high tracking accuracy, which can meet the requirements of automatic parking. Automatic parking; Vertical parking; Path tracking; Preview error; PID;Simulink/CarSim U495 A 1671-7988(2023)11-66-06 骆嫚(1986-),女,博士研究生,工程师,研究方向为自动驾驶规划、控制、感知,E-mail:tc-luoman @dfmc.com.cn。 江辉(1998-),男,研究方向为自动驾驶规划、控制,E-mail:jianghui_ecu@163.com。 10.16638/j.cnki.1671-7988.2023.011.011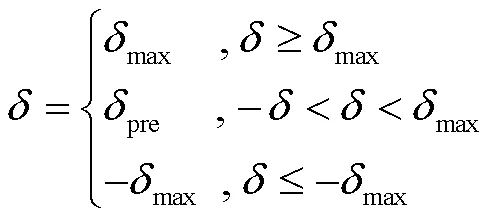
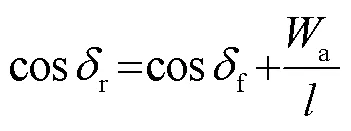
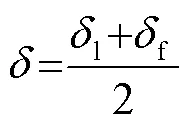
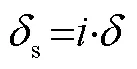
3 仿真及验证

4 结论
