无人驾驶汽车的轨迹优化研究

于 洋，徐长钊，王 钊，韩 达，张 坤

无人驾驶汽车的轨迹优化研究

于 洋，徐长钊，王 钊，韩 达，张 坤

（山东华宇工学院，山东 德州 253000）

文章重点研究无人驾驶车辆的轨迹跟踪问题，选取模型预测控制理论作为此次研究的理论基础。首先设定汽车的前轮转角作为相应的控制量，将汽车的横向位置和横摆角设置为状态量，建立起汽车的三自由度动力学模型，然后结合魔术轮胎公式，为保证模型的精度有效性，对现有模型进行线性化和离散化处理，完成预测模型的初步构想，在此基础上增加松弛因子和软约束，从而完成增量线性时变模型轨迹的建立。模型优化完成后，通过Simulink/ CarSim 联合仿真平台进行验证，设定不同仿真工况，尽可能模拟无人驾驶车辆遇到的复杂工况，经多次仿真实验，文章设计的轨迹跟踪控制器在良好路面条件下，最高安全纵向行驶速度为68 km/h，为后续无人驾驶深入研究提供数据基础。

无人驾驶车辆；模型预测控制；轨迹跟踪优化；Simulink/CarSim联合仿真

汽车技术虽然已发展多年，但在某些路面附着系数小的极端路况下，仍无法保证车辆行驶安全。随着信息通讯处理技术、传感器技术和车辆控制技术的不断发展，各汽车厂商开始研发无人驾驶技术，由于在提升汽车主动安全性、改善交通效率以及降低能耗等方面的巨大潜能，无人驾驶技术已经成为当前汽车行业的研发热点之一[1]。

1 国内外无人驾驶技术研究现状

国际方面，除了欧美传统车企，Google 和苹果等互联网公司的介入，使得无人驾驶汽车这一领域空前火爆。近十年来，谷歌科技公司进行了100多公里路程的无人实车试验，还设计了没有方向盘和踏板的样车，这是无人车研究和发展的重大突破[2]。

国内方面，多家汽车制造主机厂，诸如长安、一汽、东风、吉利等汽车公司也相继成立智能车事业部，自主或合作研制无人车项目。百度无人驾驶研究开始于2013年，其采用线性二次调节器进行轨迹跟踪控制，可完成多种工况下的轨迹跟踪任务[3]。

2 无人驾驶技术控制方法

对于无人驾驶，车辆自动转向系统在其中有非常重要的地位[4]。无人驾驶汽车能够实现的最基本要求即轨迹跟踪，但由于很难建立一个精确的非线性且高度耦合的模型，导致精确且稳定的轨迹跟踪控制成为无人驾驶技术研究中的重难点[5]。

日前众多学者对这一问题提出了多种控制方案。其中模型预测控制是带约束优化滚动求解问题的控制方法，该方法通过建立控制系统的动力学模型进而预测未来一段时间内系统的输出，通过求解带约束的最优控制问题使得系统的跟踪误差最小[6-7]。

3 增量线性时变模型预测设计

对于模型预测，其重要的要素包括三部分，即预测模型、滚动优化、反馈校正，本文将在这三个基本要素的基础上建立需要的增量线性时变模型预测轨迹跟踪器[8-9]。

3.1 预测模型

3.1.1车辆动力学单轨模型

为了提高无人驾驶汽车状态描述的准确性，选用动力学模型对车辆进行建模。将车辆底盘视为一个刚体，分别沿轴、轴和绕轴应用线性动量原理。

在轴方向上：

在轴方向上：

在轴方向上：

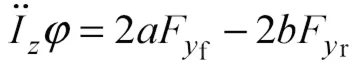
式中，、分别为质心到前、后轴的距离；为车辆整备质量；I为车辆绕轴的转动惯量；为质心横摆角。

轮胎的纵向力、侧向力可以表示为轮胎侧偏角、滑移率、路面摩擦系数和垂直载荷等参数的复杂函数为

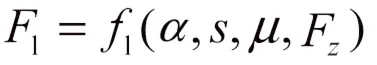
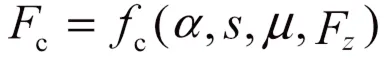
式中，为轮胎侧偏角；为滑移率；为路面摩擦系数；F为轮胎所受到的垂直载荷。

系统的状态空间表达式为

3.1.2基于魔术公式的轮胎模型

在进行汽车仿真时，轮胎所受的力和I对车辆行驶的平顺性和操纵稳定性有着重要的作用。本文研究对象为以魔术公式为基础的经验轮胎模型。

魔术公式的一般表达式为

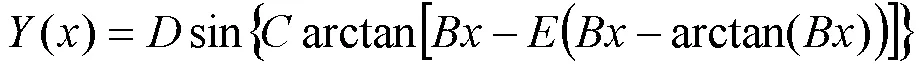
式中，为输出变量；为输入变量；为刚度因子；为形状因子；为峰值因子；为曲率因子。

利用魔术公式计算轮胎的纵向力和侧向力的关系式如下：

轮胎纵向力为

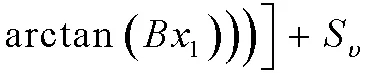
式中，

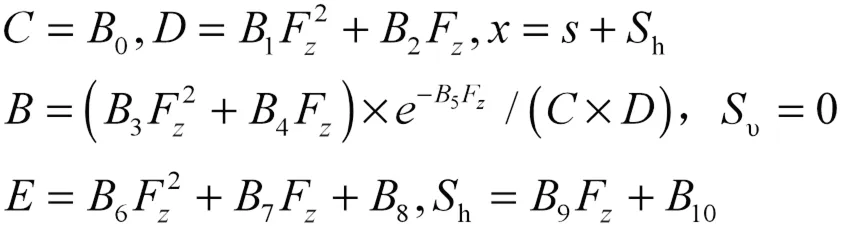
式中，为纵向滑移率；h为曲线的水平方向漂移；S为曲线的垂直方向漂移。

轮胎侧向力为

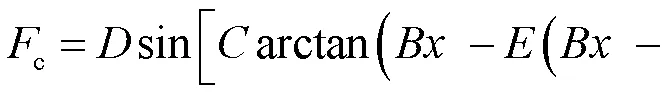
式中，

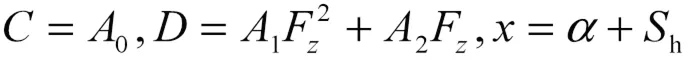
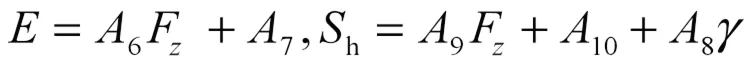
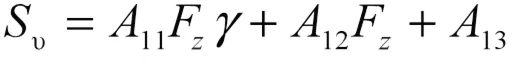
式中，为轮胎侧偏角。

在轮胎纵向力和侧向力的计算中，选择轮胎型号为 255/75 R16，相关参数如表1和表2所示。

表1 魔术公式轮胎参数1

参数CA1A2A3A4A5A6 取值1.65-341 2503 03612.80.005-0.02 参数A7A8A9A10A11A12A13 取值0.7740.0020.0130.00319.161.216.26

表2 魔术公式轮胎参数2

参数CB1B2B3B4B5 取值2.37-9.471 4911292760.088 参数B6B7B8B9B10 取值0.0040.061.210.03-0.17

轮胎侧向力计算结果如图1所示。

图1 轮胎侧向力与侧偏角关系曲线

轮胎纵向力计算结果如图2所示。

图2 轮胎纵向力与纵向滑移率关系曲线

当侧偏角在-2°与+2°之间，纵向滑移率在-5.5到5.5之间时，侧偏力和纵向力近似线性关系。

3.1.3线性、离散化

车辆在高速行驶过程中对运动控制器实时性要求很高，非线性模型预测控制难以满足，线性时变模型预测控制相对于非线性模型预测控制，有着计算量小，方便求解的特点，因此对模型进行线性化处理。

该系统在任意时刻状态量和控制量满足：

对其泰勒公式展开，进行线性优化然后整理可得

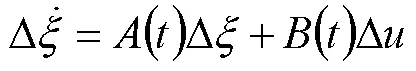
但得到的这个新的状态方程是连续性的，需要对其进行离散化处理才可以作为预测模型进行使用：

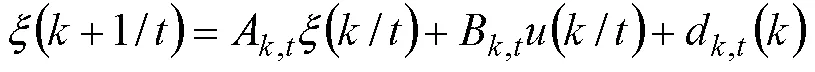
最后系统未来时刻的输出可以表示为

3.2 滚动优化

3.2.1目标函数设计

若以控制量作为目标函数中的状态量，虽然结构比较简单，较易于实现，但无法对控制增量进行精确约束，因此，本文把控制增量作为目标函数的状态量，建立增量线性时变控制器。

优化目标函数可设为以下形式：

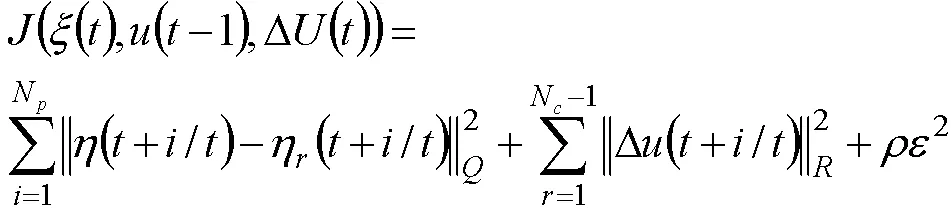
式中，为权重系数；为松弛因子；为输出偏差的权值矩阵；为控制增量的权重系数。

在实际的轨迹跟踪过程中，还需要满足系统状态量、控制量及控制增量的一些约束条件。

3.2.2约束条件设计

1.控制量约束

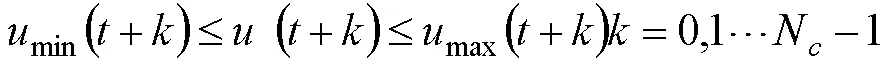
2.控制增量约束

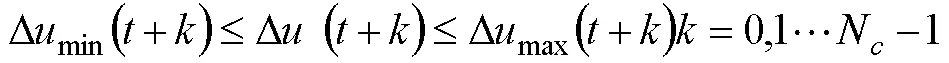
3.车辆附着条件约束

轮胎与地面附着条件制约着汽车的动力性能，因此，需要对车辆的附着条件进行约束。纵向加速度和横向加速度受到地面附着力的限制，存在如下关系：

式中，a，a分别为汽车的纵向和横向加速度。

考虑到汽车行驶过程中路况的复杂性，为避免求解失败，需要将车辆附着条件约束设为软约束。

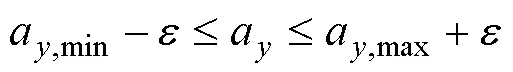
式中，a,min和a,max为加速度极限约束。

结合上述得到的预测模型及设计的优化目标函数及其约束条件，就构成了完整的增量线性时变模型预测控制器。

3.3 反馈校正

成每个控制周期内的求解后，可以得到控制时域内一系列控制增量：

将所得的控制序列的第一个元素作为实际控制输入增量加入上一节所述的未来输出量的计算中，可得到：

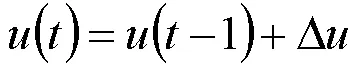
控制增量作用于系统的当前时刻，系统执行这一控制量直到下一时刻，在新的时刻，系统根据状态信息重新预测下一段时域的输出，循环往复，直到系统完成控制过程，实现最优滚动控制。

4 增量线性时变模型仿真验证

本文搭建了Simulink和CarSim联合仿真平台对模型进行验证。在车辆行驶稳定性测试方法中，双移线工况是使用频率较高的一种测试路段，本文采用双移线轨迹，通过模拟换道或紧急避障的无人驾驶车辆，对不同行驶速度下的轨迹跟踪控制器进行性能验证。

双移线轨迹方程可由期望横向位置ref和期望横摆角ref构成。横向位置和横摆角都可表示为关于纵向位置的非线性函数：

式中，

为尽可能减小轨迹跟踪误差，同时保证轨迹跟踪过程中无人驾驶车辆的稳定性。在增量线性时变模型使用的参数如表3所示。

表3 增量线性时变模型使用的参数

参数数值参数数值 NP20a1.18 NC5b1.77 m1 590Cl63 600 IZ2 385Cc60 500

4.1 CarSim汽车模型的建立

本文通过 CarSim 仿真平台建立了无人驾驶车辆的全车模型。仿真测试选用车型为通用性更强的家用轿车F-Class，具体 CarSim 整车及零部件性能参数如图 3—图5所示。

图3 CarSim整车主界面

图4 CarSim整车模型参数

图5 CarSim整车轮胎模型参数

4.2 Simulink/CarSim联合仿真

联合仿真的搭建过程会经历三个阶段。首先在 CarSim软件中根据所研究的车辆方向建立车辆模型并进行相关参数设置。

接着利用MATLAB软件的S-Function模块，结合文中第3章部分的模型算法，建立线性时变模型控制器模块。

最后，将CarSim设置的参数模型导入MATLAB软件，同时将建立的算法模型在S-Function模块中更新，之后在MATLAB/Simulink中搭建仿真框图，运行程序观测仿真结果。

4.3 仿真结果分析

在无人驾驶车辆行驶过程中，正常行驶路面的附着系数一般为0.7～1，湿滑路面附着系数一般为0.4左右。为保证仿真模拟的有效性，通过三种不同车速和路面附着系数的仿真工况进行验证，分别观测车辆行驶稳定性和控制精度与纵向行驶车速、路面附着系数之间的关系：工况一：=35 km/h，=0.7；工况二：=55 km/h，=0.7；工况三：=55 km/h，=0.4。

4.3.1工况一结果分析

由图6和图8仿真结果可知，横向位置的跟踪轨迹和期望轨迹在开始和结束阶段贴合良好，但在车辆转弯部分45～60 m、70～85 m范围内，出现较小误差，最大误差为0.13 m；由图7和图8仿真结果可知，横摆角跟踪轨迹和期望轨迹在20～100 m范围内出现轻微波动，最大误差为4°，处于可控范围内，车辆行驶稳定。

图6 横向位置轨迹跟踪对比图

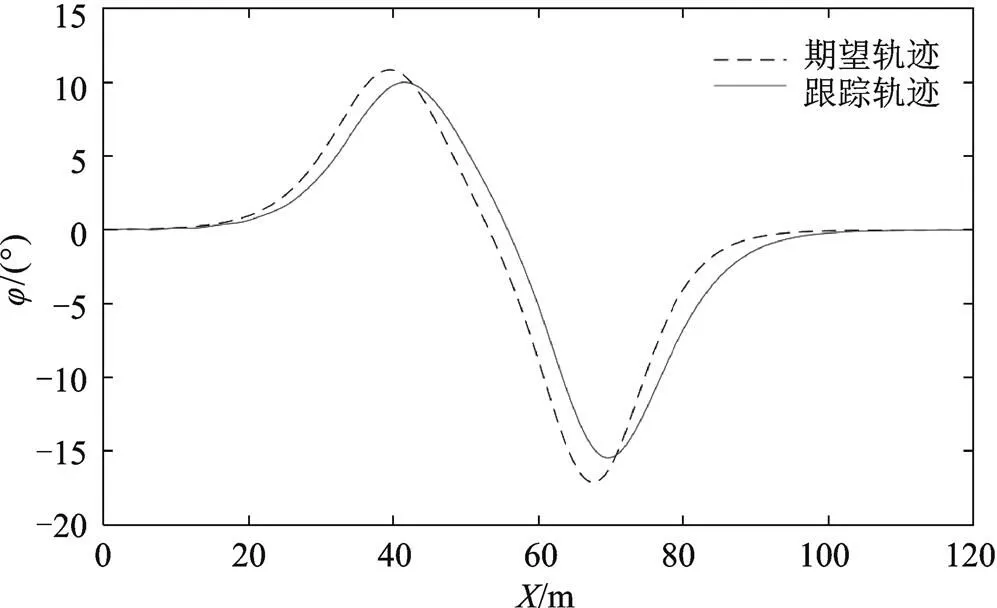
图7 横摆角轨迹跟踪对比图

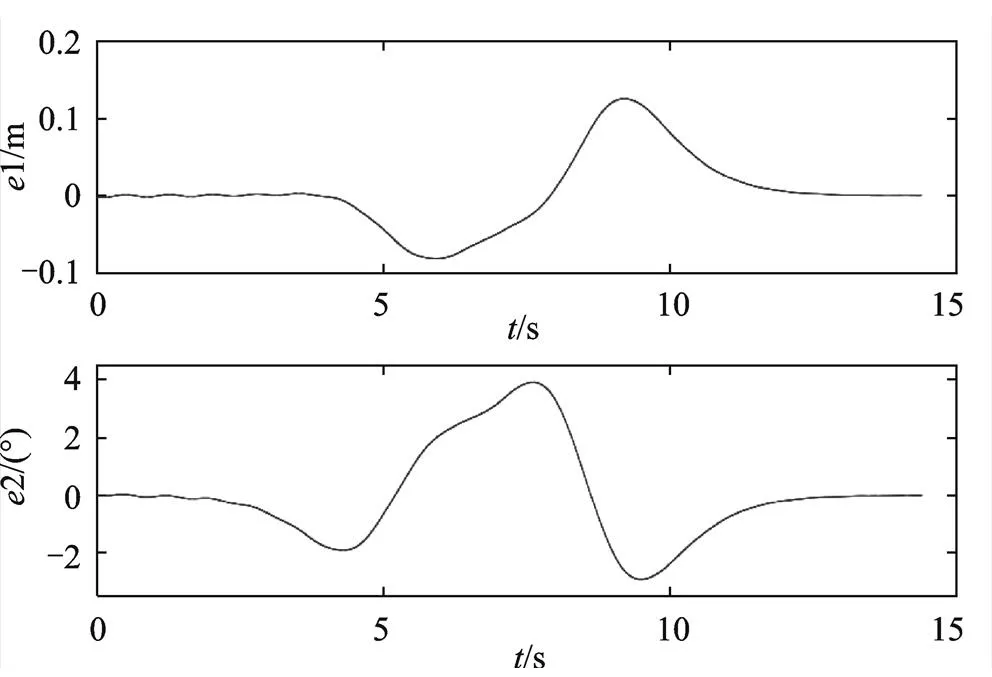
图8 横向位置和横摆角误差随时间变化关系图

4.3.2工况二结果分析

由结果可知，横向位置的跟踪轨迹和期望轨迹在开始和结束阶段表现良好，在车辆转弯部分45～60 m、65～90 m 范围内出现较小误差，最大误差为0.14 m，如图9所示；由图10和图11仿真结果可知，横摆角跟踪轨迹和期望轨迹在15～ 95 m范围内出现微小波动，最大误差为2.8°，横向位置轨迹较工况一误差增大0.01 m，横摆角轨迹较工况一误差降低1.2°，仍在可控范围内，车辆行驶稳定。

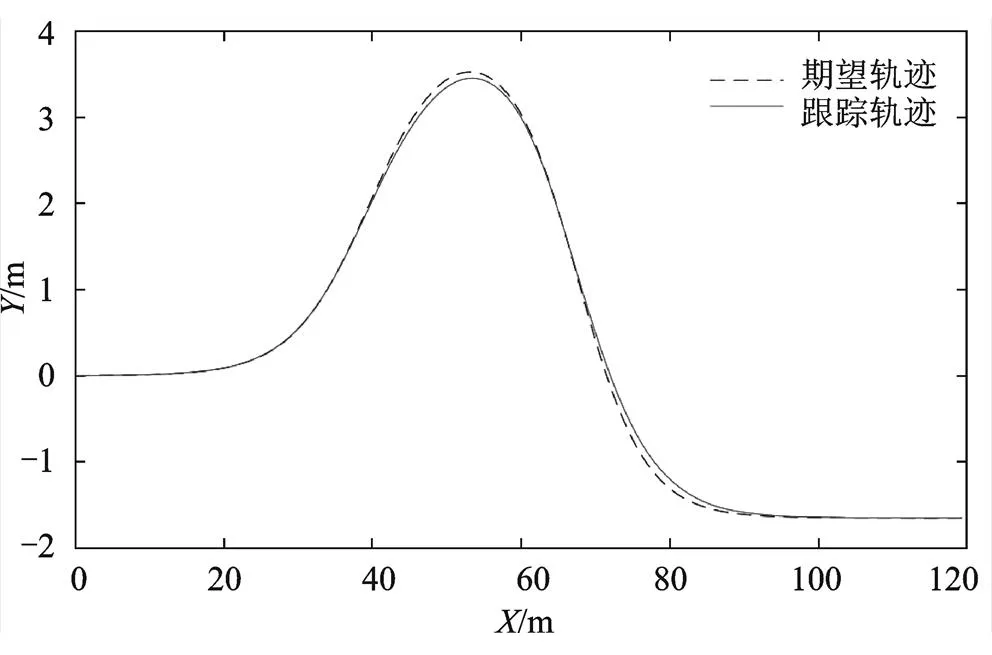
图9 横向位置轨迹跟踪对比图

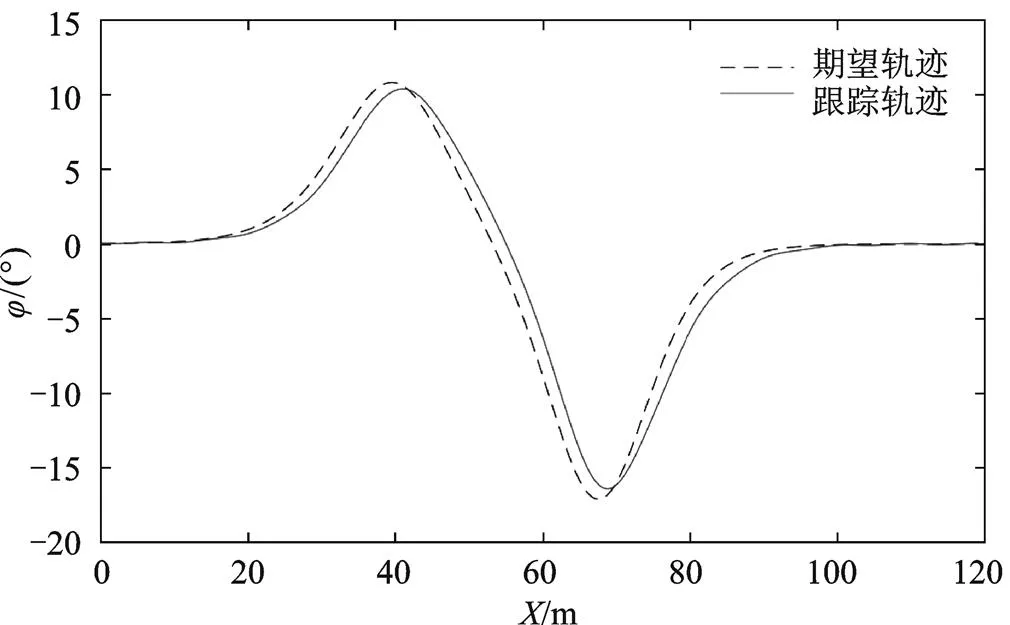
图10 横摆角轨迹跟踪对比图

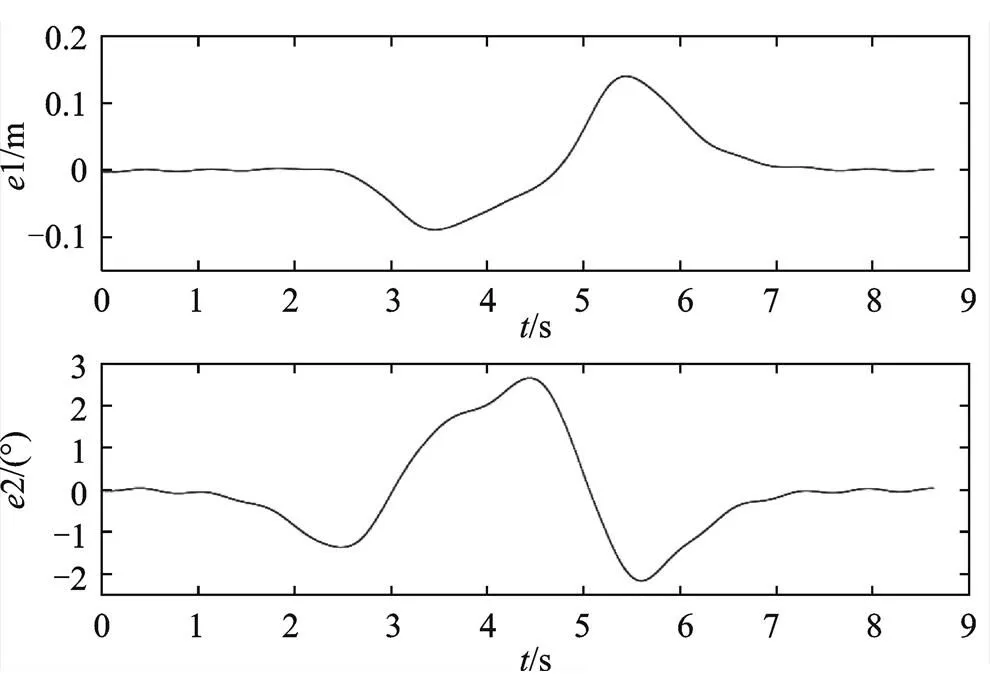
图11 横向位置和横摆角误差随时间变化关系图

4.3.3工况三结果分析

由图12—图14仿真结果可知，横向位置的跟踪轨迹和期望轨迹在开始阶段表现良好，在车辆转弯部分40～75 m范围内出现较小误差，75～120 m出现较大误差，最大误差为1.02 m；由图10和图11仿真结果可知，横摆角跟踪轨迹和期望轨迹在15～60 m范围内出现微小波动，在60～120 m范围内出现较大波动，最大误差为10.1°，横向位置轨迹较工况二误差增大0.88 m，横摆角轨迹较工况二误差增加8.9°，车辆行驶不稳定，易发生侧滑等危险工况。

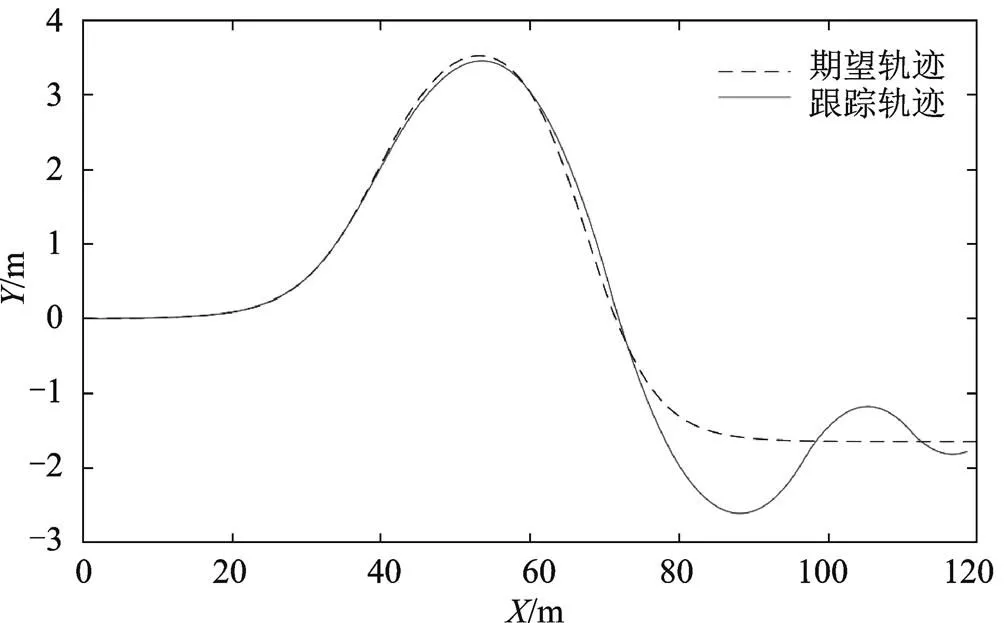
图12 横向位置轨迹跟踪对比图

图13 横摆角轨迹跟踪对比图

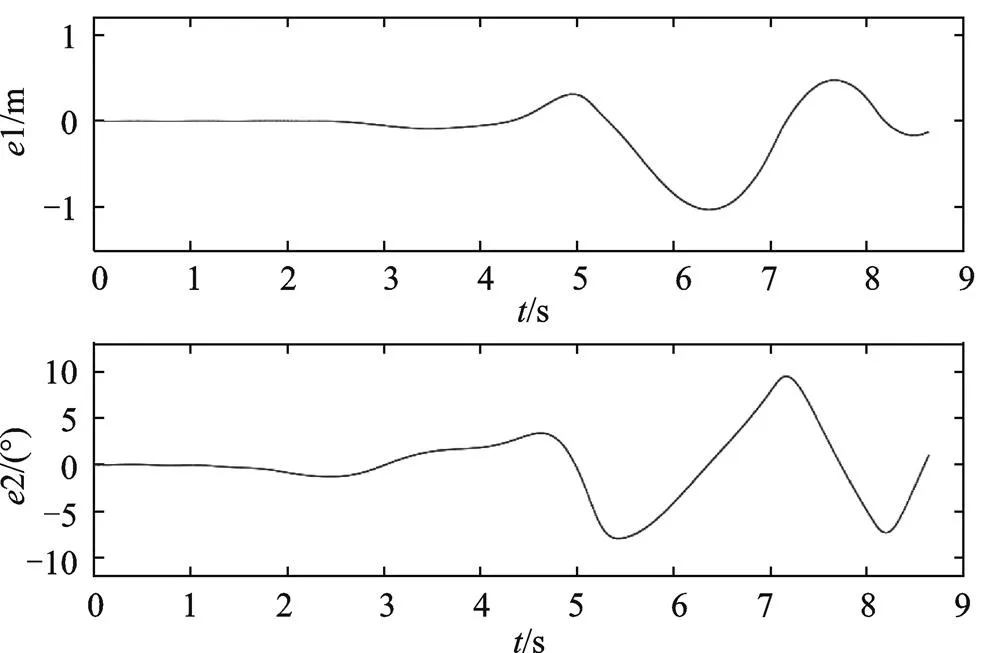
图14 横向位置和横摆角误差随时间变化关系图

5 总结

结合上述三种工况的仿真模拟，可以发现在车辆行驶过程中，随着车辆纵向行驶速度的增大或路面附着系数的降低，构建的轨迹跟踪控制器的跟踪误差也在不断增大，此时车辆就会不可避免发生行驶不稳定，易发生方向失控、侧滑等危险工况。

此外，经多次Simulink仿真实验结果可知，轨迹跟踪控制器的最高安全纵向行驶速度为 68 km/h，当车辆行驶速度超过该值时，跟踪轨迹明显偏离期望轨迹，误差急剧增大，车辆处于极不稳定行驶工况。

[1] 姜岩,陈慧岩,熊光明,等.无人驾驶汽车概论[M].北京:北京理工大学出版社,2014.

[2] 赵禹程,张永伟,俞乔.无人驾驶汽车发展史､技术现状与创新管理模式研究[J].新疆师范大学学报(哲学社会科学版),2021,42(4):103-112.

[3] 余世全.无人驾驶汽车的发展现状和相关建议[J].专用汽车,2023(1):11-14.

[4] 姜岩,赵熙俊,龚建伟,等.简单城市环境下地面无人驾驶系统的设计研究[J].机械工程学报,2012,48(20): 103-112.

[5] 李培新,姜小燕,魏燕定,等.基于跟踪误差模型的自动驾驶车辆预测控制方法[J].农业机械学报,2017 (10):351-357.

[6] 龚建伟,姜岩,徐威.无人驾驶车辆模型预测控制[M].北京:北京理工大学,2014.

[7] 邹凯,蔡英凤,陈龙,等.基于增量线性模型预测控制的无人车轨迹跟踪方法[J].汽车技术,2019(10):1-7.

[8] 孙银健.基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究[D].北京:北京理工大学,2015.

[9] 明廷友.智能汽车的轨迹跟随控制研究[D].长春:吉林大学,2016.

Research on Trajectory Optimization of Driverless Vehicles

YU Yang, XU Changzhao, WANG Zhao, HAN Da, ZHANG Kun

( Shandong Huayu University of Technology, Dezhou 253000, China )

This paper focuses on the trajectory tracking problem of unmanned vehicles. On the basis of selecting model predictive control theory as the theoretical basis of this study, firstly set the front wheel angle of the vehicle as the corresponding control quantity, and set the lateral position and yaw angle of the vehicle as the state quantity to establish the three-degree-of-freedom dynamic model of the vehicle. Then, combined with the magic tire formula, in order to ensure the accuracy and effectiveness of the model, the existing model is linearized and discretized to complete the preliminary conception of the prediction model. On this basis, the relaxation factor and soft constraint are added to complete the establishment of the incremental linear time-varying model trajectory. After the model optimization is completed,it is verified through the Simulink/CarSim joint simulation platform.By setting different simulation conditions, simulated the complex working conditions encountered by the driverless vehicle as much as possible. After several simulation experiments, the trajectory tracking controller designed in this paper is under good road conditions. The maximum safe longitudinal driving speed is 68 km/h, which provides a data basis for subsequent in-depth research on driverless vehicles.

Driverless vehicles;Model predictive control;Trajectory tracking optimization;Simulink/CarSim co-simulation

U495

A

1671-7988(2023)11-49-08

于洋（1989－），男，在职硕士研究生，工程师，研究方向为新能源汽车动力电池，E-mail:jsanjian@sina.com。

依托山东华宇工学院德州市电动汽车动力控制与调试重点实验室（6）。

10.16638/j.cnki.1671-7988.2023.011.009