基于风洞试验数据和仿真融合修正的气动特性预示技术

刘汉宇，张耘隆，张津泽，胡彦辰，袁 赫

基于风洞试验数据和仿真融合修正的气动特性预示技术

刘汉宇，张耘隆，张津泽，胡彦辰，袁 赫

（北京宇航系统工程研究所，北京，100076）

为提升运载火箭气动特性数值仿真预示精度，降低型号研制成本、缩短研制周期，提出了一种基于风洞试验数据和CFD数值仿真结果融合修正的火箭气动特性精确预示方法。以多组光杆构型火箭仿真计算结果和单个类似构型风洞试验数据为基础，建立了风洞试验与数值仿真计算结果融合修正模型，以获取未开展风洞试验构型的气动特性数据。经数据融合修正后的火箭气动特性数据已成功用于型号设计，并取得了较好的效果。

数据融合；气动特性修正；数值仿真；风洞试验

0 引 言

气动特性预示是运载火箭总体设计工作中的重要环节，预示精度直接影响火箭的弹道设计精度、姿态控制品质及运载能力，气动特性偏差较大情况下甚至会影响型号任务的成败[1-4]。近年来，随着中国航天事业快速发展，型号研制任务和发射量逐年攀升，诸多运载型号需要在原构型基础上局部调整气动外形（包括但不限于更换整流罩，部段局部增长、缩短等），若重新开展风洞试验将导致型号研制经费和任务周期难以得到保障，亟需发展一种在开展少量风洞试验情况下即可获得运载火箭高精度气动数据库的方法，以降低运载火箭风洞试验成本，加快型号研制进度。

随着计算机技术和人工智能技术的发展，基于近似模型的设计方法广泛应用于飞行器气动特性预示及优化设计等领域，通过建立数学模型获得输入数据和输出参数的关系，完成设计空间内未知设计点响应值的快速评估[5]。工程上常用的近似模型主要包括Kriging代理模型[6]、径向基函数（Radial Basis Function，RBF）[7]、响应面模型（Response Surface Methed，RSM）[8]、支持向量回归模型（Support Vector Regression，SVR）等。上述近似模型为固定置信度近似模型，模型精度对输入数据的精度较敏感，为保证模型的精度可以满足工程需要，一般需要大规模的试验数据和高精度仿真数据作为模型输入样本，构建模型所需仿真时间和成本较高。

针对上述问题，变置信度数据融合模型得到发展。变置信度数据融合模型是一种先应用样本量较多的低精度数据构建数据沿自变量变化趋势，再通过样本量较少的高精度数据对模型进行修正，明确高低精度数据间的函数关系，实现融合后的数据收敛于高精度数据的方法[9-10]，极大程度上降低了近似模型对高精度数据样本的需求。

常用的变置信度模型包括标度函数修正模型、空间映射模型、Co-Kriging类模型、神经网络模型等[7]。Chang[11]和Haftka[12]最早提出了比例缩放标度函数修正模型，建立高低精度数据比例缩放函数使低精度数据局部收敛于高精度数据；Dudley[13]在NASA民用运输技术中将标度函数修正模型应用于气动特性数据处理中；Alexandrov[14-15]基于增量标度和比例缩放标度函数修正模型提出了一种混合标度函数修正模型，并将其成功应用于三维机翼优化设计中；杜涛[9]提出了一种针对混合标度函数修正模型自适应预处理技术，提升了原始数据绝对值较小状态下近似模型的鲁棒性；Wang[16]基于最小二乘法提出了一种增量修正标度函数修正模型构建方式，提升了模型的精度；Bandler[17]提出了空间映射模型，在设计空间内建立了高低精度数据的映射关系，提升了模型的泛化能力；Kennedy[18]最早将Co-Kriging类模型应用于工程，并提出了KOH模型；Meng[19]在多可信度神经网络模型基础上提出了基于多可信度的贝叶斯神经网络模型。

为解决运载火箭研制高效率、低成本需求和型号气动特性数据精确性之间的矛盾，本文基于标度函数修正数据融合模型，提出一种基于相似构型火箭标度函数修正气动特性预示方法，以光杆构型火箭仿真计算结果和单个类似构型风洞试验数据为基础，在未重新开展风洞试验情况下获取相似构型火箭气动特性，该方法已成功应用于型号设计，验证了方法的适用性。

1 标度函数修正模型

标度函数修正模型是一种以低精度输入数据为基础，通过在设计空间内构建标度函数进而建立低精度数据和高精度数据间函数关系的数据融合模型，最常用的3种标度函数修正模型如下。

1.1 增量标度函数修正模型

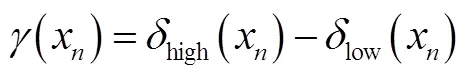
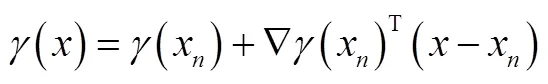
1.2 比例缩放标度函数修正模型

1.3 混合标度函数修正模型

2 标度函数修正模型适应性验证

为验证标度函数修正模型对于运载火箭气动特性预示的适应性，本文基于少量的风洞试验数据（高精度数据）和CFD数值仿真计算结果（低精度数据），建立了典型运载火箭构型气动特性数据库，对3种标度函数修正模型的精度进行考核。

2.1 气动特性高低精度数据

构建运载火箭气动特性近似模型所需的高精度气动数据来源于风洞试验结果，数据精度满足型号设计需求。低精度数据来源于CFD数值仿真计算，数值仿真计算控制方程求解、边界条件设置、数值方法及计算网格如下。

2.1.1 控制方程

本文计算求解的流体控制方程为雷诺平均的N-S方程：

2.1.2 边界条件

火箭壁面采用无滑移绝热壁面边界条件：

外部远场采用压力远场边界条件，给定来流马赫数、温度和压强条件，流场出口采用压力出口边界条件，给定环境压强。

2.1.3 数值方法

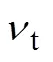
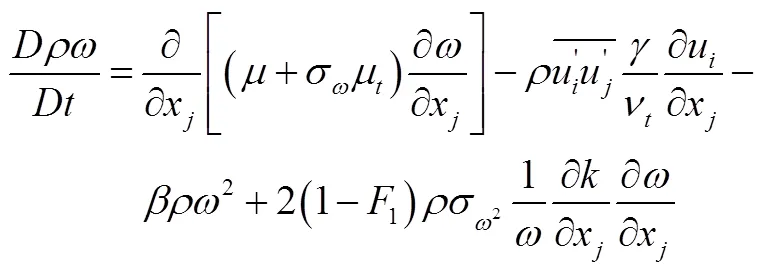
2.1.4 计算网格

计算网格采用结构化网格，在箭体近壁面进行了局部加密，流场典型截面网格分布情况见图1。

图1 流场典型截面计算网格分布

2.2 标度函数修正模型精度校核

图2给出了火箭法向力系数n随马赫数变化无量纲化曲线。图2中CFD数值计算结果与风洞试验结果差异较大，直接应用CFD仿真结果将导致设计存在风险。为了考核标度函数修正模型的精度，选择=0.4、0.8、1.0、1.5、3.0、5.0工况风洞试验高精度数据对模型进行修正，以其他状态风洞试验结果对模型进行校核。模型响应结果表明，在亚声速和超声速状态，3种标度函数修正模型法向力系数响应值均和风洞试验数据吻合较好。在跨声速状态下增量标度函数修正模型及混合标度函数修正模型均出现了不同程度的振荡失真。比例缩放函数修正模型得到的结果更趋近于试验结果。

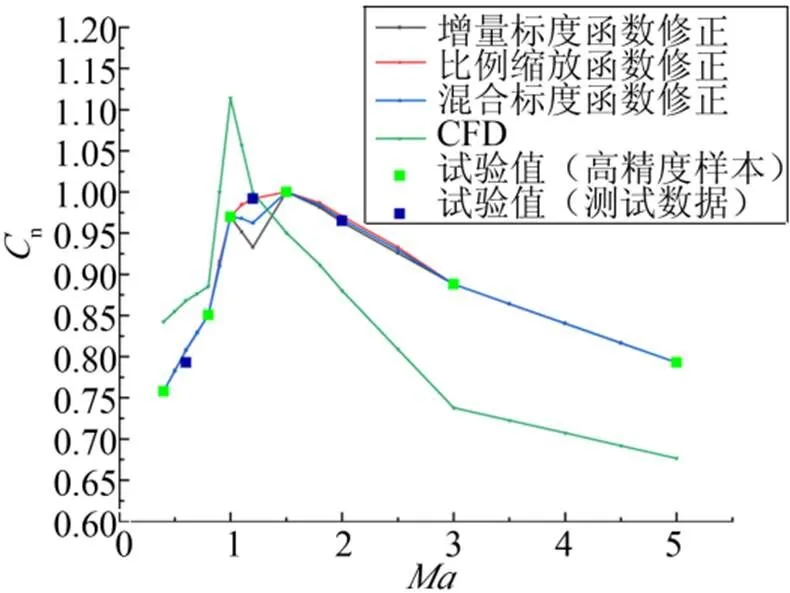
图2 经标度函数修正模型修正后法向力系数

混合模型在获得增量修正模型和比例缩放模型优势的同时，也相应继承了二者的缺点，故在=1.2时法向力系数响应值也出现了失真情况，对于增量修正模型和比例缩放模型适用区间存在差异问题，可以应用混合模型提升模型预示精度。

图3为火箭压心系数cp随变化无量纲化曲线。

图3 经标度函数修正模型修正后压心系数

由图3可知，CFD数值计算结果与风洞试验结果随变化趋势较为吻合，在量级上具有一定差异。同样选择=0.4、0.8、1.0、1.5、3.0、5.0工况风洞试验高精度数据对模型进行修正，以其他状态风洞试验结果对模型进行校核。模型响应结果表明，3种标度函数修正模型压心系数响应值和风洞试验数据吻合较好。在=2.0时，3种模型响应值均略大于试验结果，主要原因为模型输入数据较稀疏，增大高精度数据覆盖范围可有效解决该问题。在=1.2左右时，比例缩放标度修正模型的效果仍优于其他2种模型。

3 相似构型火箭气动特性数据融合模型

使用前文所述标度函数修正模型可以基于少量风洞试验数据和CFD数值仿真数据建立单一火箭构型气动特性数据库。但对于未开展风洞试验、缺少高精度数据输入的火箭构型，常规近似模型无法进行高精度气动特性数据建模。

根据运载型号气动特性规律，构型不产生显著布局差异情况下，CFD数值仿真计算可近似描述火箭气动特性变化规律，指导型号研制，相似构型火箭气动外形如图4所示。

图4 相似构型火箭气动外形

本文基于对运载火箭重要气动特性参数近似能力更优的比例缩放标度函数修正模型，建立相似构型火箭比例缩放标度函数修正模型，基于基础构型火箭风洞试验数据、基础构型CFD数值仿真数据及相似构型CFD数值仿真数据，在不重新开展风洞试验情况下完成相似构型火箭气动特性建模。

模型的数学描述为

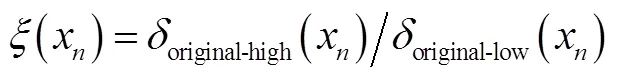
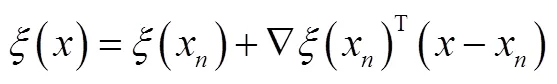
对基于相似构型火箭比例缩放标度函数修正模型建立了相似构型火箭气动特性数据库。为尽可能提升模型精度，以基础构型全飞行剖面Ma状态下风洞试验高精度气动特性数据作为模型输入，辅以CFD数值仿真结果，完成了相似构型火箭气动特性预示。箭体法向力系数及压心系数预测值如图5、图6所示，数据均经过归一化无量纲处理，基于修正模型预示的火箭气动特性与试验数据吻合较好，验证了相似构型火箭气动特性数据融合模型的预示精度满足工程研制需求。目前相似构型火箭气动特性数据融合模型已成功应用于运载火箭型号设计，并取得了预期的效果。

图6 相似构型火箭压心系数预示

4 结束语

本文将变置信度数据融合技术应用于现役火箭气动特性数据库构建中。研究发现对于近似模型输入数据的差量相对于数据绝对值整体比例较小情况下，比例缩放标度函数修正模型鲁棒性较优。在此基础上提出了相似构型火箭气动特性数据融合模型，基于基础构型火箭气动特性风洞试验数据和CFD数值仿真结果，在不重新开展风洞试验情况下构建相似构型运载火箭气动特性数据库，相似构型火箭气动特性数据融合模型已成功应用于运载火箭型号设计，并取得了预期的效果。

[1] 李金晟, 庄凌, 宋加洪, 等. 适用于工程数据的飞行器气动特性修正框架[J]. 航空学报, 2022, 43(5): 201-214.

LI Jinsheng, ZHUANG Ling, SONG Jiahong, et al. Aircraft aerodynamic characteristic correction framework for engineering data[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(5): 201-214.

[2] 邓晨, 陈功, 王文正, 等. 基于飞行试验和风洞试验数据的融合算法研究[J]. 空气动力学学报, 2022, 40(6): 45-50.

DENG Chen, CHEN Gong, WANG Wenzheng, et al. Research on the data fusion algorithm based on flight test data and wind tunnel test data[J]. Acta Aerodynamica Sinica, 2022, 40(6): 45-50.

[3] 董超, 甄华萍, 陈刚, 等. 非圆截面弹体高超声速气动特性研究[J]. 导弹与航天运载技术, 2015(4): 11-15.

DONG Chao, ZHEN Huaping, CHEN Gang, et al. Investigation on hypersonic aerodynamic characteristics ofnoncircular cross sectionmissile body[J]. Missiles and Space Vehicles, 2015(4): 11-15.

[4] 钟震, 朱广生, 李强. 固体运载器主动段气动参数辨识方法[J]. 导弹与航天运载技术, 2018(6): 1-6.

ZHONG Zhen, ZHU Guangsheng, LI Qiang. Parameter identification method of aerodynamic data for solid launch vehicle in boost phase[J]. Missiles and Space Vehicles, 2018(6): 1-6.

[5] 周奇, 杨扬, 宋学官, 等. 变可信度近似模型及其在复杂装备优化设计中的应用研究进展[J]. 机械工程学报, 2020, 56(24): 219-245.

ZHOU Qi, YANG Yang, SONG Xueguan, et al. Survey of multi-fidelity surrogate models and their applications in the design and optimization of engineering equipment[J]. Journal of Mechanical Engineering, 2020, 56(24): 219-245.

[6] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225.

HAN Zhonghua. Kriging surrogate model and its application to design optimization[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225.

[7] 徐家宽, 白俊强, 黄江涛, 等. 考虑螺旋桨滑流影响的机翼气动优化设计[J]. 航空学报, 2014, 35(11): 2910-2920.

XU Jiakuan, BAI Junqiang, HUANG Jiangtao, et al. Aerodynamic optimization design of wing under the interaction of propeller slipstream[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2910-2920.

[8] 李国帅, 魏志, 李巍, 等. 现代试验设计方法在高速风洞试验中的应用[J]. 航空学报, 2015, 36(3): 782-788.

LI Guoshuai, WEI Zhi, LI Wei, et al. Using modern design of experiments methodologies for high speed wind tunnel tests[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 782-788.

[9] 许晨舟, 杜涛, 韩忠华, 等. 机器学习数据融合方法在火箭子级栅格舵气动特性建模应用中的比较研究[J]. 实验流体力学, 2022, 36(3): 79-92.

XU Chenzhou, DU Tao, HAN Zhonghua, et al. Comparison of machine learning data fusion methods applied to aerodynamic modeling of rocket first stage with grid fins[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(3): 79-92.

[10] 杜涛, 陈闽慷, 李凰立, 等. 变精度模型(VCM)的自适应预处理方法研究[J]. 空气动力学学报, 2018, 36(2): 315-319.

DU Tao, CHEN Minkang, LI Huangli, et al. Research on adaptive preconditioning method for variable complexity model[J]. Acta Aerodynamica Sinica, 2018, 36(2): 315-319.

[11] CHANG K J, HAFTKA R T, GILES G L, et al. Sensitivity based scaling for approximating structural response[J]. Journal of Aircraft, 1993, 30(2): 283-288.

[12] HAFTKA R T. Combining global and local approxima tions[J]. AIAA Journal, 1991, 29(9): 1523-1525.

[13] DUDLEY J, HUANG X, MACMILLIN E, et al. Multidisciplinary optimization of the high-speed civil transport[R]. AIAA-95-0125, 1995.

[14] ALEXANDROV N M, DENNIS J E, LEWIS R M, et al. Atrustregion framework for managing the use of approximation models in optimization[J]. Structural Optimization, 1998, 15(1): 16-23.

[15] ALEXANDROV N, NIELSEN E, LEWIS R, et al. First-order model management with variable-fidelity physicsapplied to multi-element airfoil optimization[C]. Long Beach: Proc of the 8th Symposium on Multidisciplinary Analysis and Optimization, 2000.

[16] WANG S, LIU Y, ZHOU Q, et al. A multi-fidelity surrogate model based on moving least squares: fusing different fidelity data for engineering design[J]. Structural and Multidisciplinary Optimization, 2021, 64(6): 3637-3652.

[17] BANDLER J W, BIERNACKI R M, CHEN S H, et al. Space mapping technique for electromagnetic optimization[J]. IEEE Transactions on Microwave Theory and Techniques, 1994, 42(12): 2536-2544.

[18] KENNEDY M, O'HAGAN A. Predicting the output from a complex computer code when fast approximations are available[J]. Biometrika, 2000, 87(1): 1-13.

[19] MENG X H, KARNIADAKIS G E. A composite neuralnetwork that learns from multi-fidelity data: application tofunction approximation and inverse PDE problems[J]. Journal of Computational Physics, 2020, 401. DOI: 10.1016/j.jcp.2019.109020.

Aerodynamic Characteristics Prediction based on Wind Tunnel Test Data and Simulation Fusion Correction Technology

LIU Hanyu, ZHANG Yunlong, ZHANG Jinze, HU Yanchen, YUAN He

(Beijing Institute of Autronautical Systems Engineering, Beijing, 100076)

In order to improve the accuracy of numerical simulation prediction of aerodynamic characteristics of carrier rocket, reduce the cost of development and shorten the development period, an accurate prediction method of aerodynamic characteristics of rocket is proposed based on the fusion correction of wind tunnel test data and CFD numerical simulation results. Based on the simulation results of the rod configuration rocket and the wind tunnel test data of similar configuration, a modified model of fusion of wind tunnel test and numerical simulation results is established to obtain the aerodynamic characteristics data of the configuration without wind tunnel test. The aerodynamic characteristics of rocket modified by data fusion have been successfully used in carrier rocket design and achieved results expected.

data fusion; aerodynamic characteristic correction; numerical simulation; wind tunnel test

2097-1974(2023)02-0097-06

10.7654/j.issn.2097-1974.20230219

V475.1

A

2022-11-29；

2023-03-15

军委科技委基础加强计划技术领域基金（2022-JCJQ-JJ-0640）

刘汉宇（1995-），男，助理工程师，主要研究方向为运载火箭气动力热设计。

张耘隆（1986-），男，高级工程师，主要研究方向为运载火箭气动力热设计。

张津泽（1991-），男，工程师，主要研究方向为运载火箭气动力热设计。

胡彦辰（1993-），男，工程师，主要研究方向为运载火箭气动力热设计。

袁 赫（1993-），男，工程师，主要研究方向为运载火箭载荷与力学环境设计。