VICKF-IMM算法在机动目标跟踪中的应用

王帅祥

VICKF-IMM算法在机动目标跟踪中的应用

王帅祥

（中北大学机电工程学院，太原，030051）

针对智能体移动方式复杂，对其进行观测的传感器测量的信息存在噪声以及目标运动轨迹发生突然的改变会导致目标观测失真甚至错误的问题，提出了一种变积容积卡尔曼滤波交互多模型算法（VICKF-IMM）。该算法将容积卡尔曼滤波与交互多模型算法相结合，并对容积卡尔曼滤波（CKF）中球面积分进行变积分转换处理。优化了其积分求解的方式，提高了整体的稳定性。Monte-Carlo仿真分析，与CKF-IMM和UKF-IMM算法相比，该算法的跟踪精度有明显的提高，并在目标运动发生突变时有更高的稳定性。

SCKF-IMM；机动目标跟踪；容积卡尔曼滤波；交互多模型算法

0 引 言

信息化时代针对智能体的跟踪定位是当前研究的新目标，但智能体的移动往往不是单一模式下的运动，其运动模式复杂多变，且其运动模式随时间变化而改变。并且在对目标的观测过程中往往会受到量测相关的噪声影响，造成定位精度的下降。

为了使算法能准确描述目标的状态，1988年，Blom等[1]提出交互多模型算法。但交互多模型算法一般会配合滤波算法进行使用，传统的卡尔曼滤波针对非线性系统的解决能力不足，所以Arasaratnam将贝叶斯估计和容积变换有机结合提出了一种非线性滤波算法[2]，即容积卡尔曼滤波算法（Cubature Kalman Filter，CKF），它能计算出一些具有相同权重的点，并可直接通过非线性系统方程对系统中的状态和误差进行迭代的估计，其精度一般可达到3阶展开的程度[3]。

但容积卡尔曼滤波算法必须将非线性函数分解成球面积分和径向积分的形式，求解其积分的过程比较复杂，传统方式精度不高。

针对这种类型情况，本文提出变积容积卡尔曼滤波交互多模型算法（Variable Cubature Kalman Filter Interactive Multiple Model Algorithm，VICKF-IMM）。该算法以CKF为基础，改变了其中径向积分的求解方式，再融合自适应交互多模型算法，使其更加适应复杂多变的智能体目标跟踪领域。

1 系统模型

当目标个体在观测区域进行运动时，一般的观测器如雷达、红外等可以将其在图像中投影位置获得的偏置角度作为其相关变量。其观测目标如图1所示。

图1 观测器观测目标

由图1中角度相关关系可以推导出观测器观测出来的估计夹角。其推导公式如下：

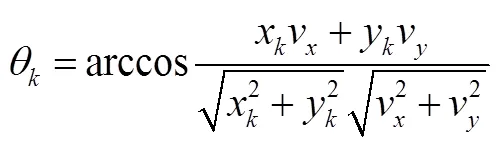
笛卡尔坐标系下对目标运动进行建模。在对移动智能体目标进行运动学分析时，可以假设目标以某种运动模型进行运动，对目标建模一般会达到更好的跟踪效果，在考虑到观测器观测时，要考虑到其噪声的存在，故建立的状态方程和观测方程如下：

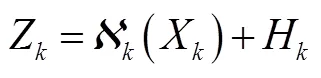
2 变积容积卡尔曼滤波算法

2.1 容积卡尔曼滤波算法

CKF算法的核心思想是采用球面-径向容积规则，近似处理非线性传递的后验估计值和相应的协方差。

CKF存在计算容积点，而后利用2个容积位置计算出来的点进行加权求和来近似高斯积分。其数学表示为

2.2 传统求解方式

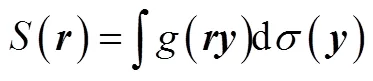
其球面积分可以用容积准则来表示：

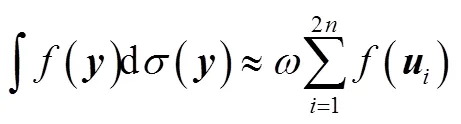
2.3 改进积分求解方式

由于传统的径向基求解方式，较为复杂，这里对径向积分进行变积分求解。引用定理1——相径积分可通过r个点的高斯形式的求积准则，进行求解工作，其求解公式为

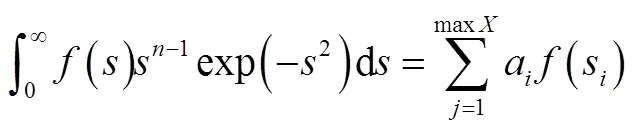
径向积分可以通过高斯-拉尔盖积分进行表示：

并且因为球面容积准则的对称性，可以将式（12）的结论部分进行简化：

使用这种方式，可简化径向积分的求解方式，且与交互多模型算法相结合，就构成VICKF-IMM算法的全部过程。

3 数字实验仿真与分析

3.1 仿真条件

假设目标运动模式的模型集中含有匀速直线运动（CV）、匀加速直线运动（CA）和协同的圆周转弯运动（CT）等运动模式集合，并且目标在运动过程中其运动模式，会随时发生改变。

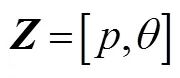
假定当前选定的目标的起始位置为（30 000， 20 000），目标的初始速度在轴分量V=80，在轴分量V=50，且目标将在上一节介绍的3种运动形式中随机产生运动变化，预设目标运行的总时间为350 s。

模型状态转移矩阵的初始化设置为针对CA，CV，CT模型的概率状态初始值设置为[0.6；0.2；0.2]。相应的交互多模型中的马尔科夫概率转移矩阵的初始为

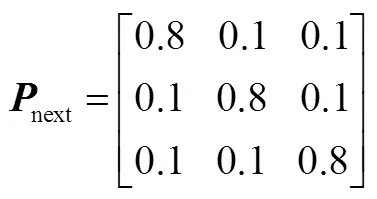
本文将仿真中的噪声简化为高斯白噪声，其均值为0，方差为Q=0.13I，采用蒙特卡洛方法进行120次仿真实验。本次仿真中将CKF-IMM、UKF-IMM和VICKF-IMM算法进行对比。实际仿真过程目标运动的位置如图2所示。

从图2可分析出，3种算法都能对包含CV、CA和CT模型集的目标机动进行跟踪。下面将详细分析其算法的优劣。

算法性能评价指标在大多数标准中为均方根误差：

目标运动实际参数轨迹中加速度预设情况见表1。

表1 探测中的目标运动加速度变化情况

Tab.1 Changes in target motion acceleration during detection

目标机动时刻sX方向加速度m·s-2Y方向加速度m·s-2Z方向加速度m·s-2 13613160 150-680 2639-90 289430 302-580

3.2 仿真分析

仿真结果中，本文算法VICKF-IMM、CKF-IMM和UKF-IMM都可以对目标运动进行有效的跟踪，其位置均方根误差对比如图3所示。由图3分析可知，VICKF-IMM算法的定位精度比UKF-IMM算法高61.1%，VICKF-IMM算法的定位精度比CKF-IMM算法提高51.6%，其位置均方根误差平均下降60.1%。

图3 不同算法位置均方根误差对比

CKF-IMM和UKF-IMM算法中，其定位位置在40 s发生突变，而本文算法的定位精度改变较小，所以VICKF-IMM算法的稳定性比传统的CKF-IMM算法和UKF-IMM算法的高，鲁棒性表现更好。

图4为VICKF-IMM、CKF-IMM和UKF-IMM算法的速度均方根误差。图4表明其速度均方根误差下降32%。

图4 不同算法速度均方根误差对比

4 结 论

综上所述，本文提出的方法优点可总结为以下几方面：

a）通过改变并简化求其球面积分方式，简化了计算难度，并提高了相关跟踪精度，在CA、CV、CT传统的模型级突变算例中，其跟踪精度在位置属性上提高约60%，速度属性的精度提高了32%；

b）优化了传统算法的处理步骤，避免了传统CKF算法中计算数值时误差累计造成的过程误差分解的错误，VICKF-IMM算法稳定性（鲁棒性）相比传统型算法有所提高。

[1] 张冉, 杜清, 万岳, 等. 一种基于交互多模型卡尔曼滤波的被动协同定位滤波算法研究[J]. 雷达与对抗, 2023, 43(1): 9-12.

ZHANG Ran, DU Qing, WAN Yue, et al. Research on passive collaborative positioning filtering algorithm based on interactive multi-model Kalman filter[J]. Radar and Countermeasures, 2023, 43(1): 9-12.

[2] 封普文, 黄长强, 曹林平, 等. 基于自适应马尔可夫参数交互多模型算法的弹道导弹跟踪研究[J]. 兵工学报, 2014, 35(12): 2041-2049.

FENG Puwen, HUANG Changqiang, CAO Linping, et al. Research on ballistic missile tracking based on adaptive markov parameter interactive multi-model algorithm[J]. Acta Armamentarii, 2014, 35(12): 2041-2049.

[3] 兰义华, 任浩征, 张勇, 等. 一种基于“当前”模型的改进卡尔曼滤波算法[J]. 山东大学学报（工学版）, 2012, 42(5): 12-17.

LAN Yihua, REN Haozheng, ZHANG Yong, et al. An improved Kalman filter algorithm based on "current" model[J]. Journal of Shandong University (Engineering Science), 2012, 42(5): 12-17.

[4] Aryal A, Ghahramani A, Becerik Gerber B. Monitoring fatigue in construction workers using physiological measurements[J]. Automation in Construction, 2020, 82(10): 2999-3007.

Application of VICKF-IMM Algorithm in Maneuvering Target Tracking

WANG Shuaixiang

(College of Mechanical and Electrical Engineering, North University of China, Taiyuan, 030051)

In the process of tracking targets with complex and variable motion patterns during movement, there is noise in the information measured by the sensors that observe them, and sudden changes in the target's motion trajectory can lead to distortion or even errors in the target observation. A variable cubature Kalman filter interacting multiple model algorithm (VICKF-IMM) is proposed. This algorithm combines volumetric Kalman filtering with interactive multiple model algorithm, and performs variable integral transformation on the spherical surface integral in cubature Kalman filtering. The optimization of its integral solution method has improved overall stability. Monte Carlo simulation analysis shows that compared with CKF-IMM and UKF-IMM algorithms, the tracking accuracy of this algorithm is significantly improved, and it has higher stability in case of sudden changes in target motion.

SCKF-IMM; maneuvering target tracking; cubature Kalman filter; interactive multiple model algorithm

2097-1974(2023)02-0016-04

10.7654/j.issn.2097-1974.20230204

TN953

A

2023-04-01；

2023-04-03

王帅祥（1996-），男，硕士研究生，主要研究方向为探测与预测。