基于不确定性的输气管道水合物生成概率分析与研究
2023-06-18吴振宙赵恺锋徐佳蒋起祯倪凯马庆然
吴振宙 赵恺锋 徐佳 蒋起祯 倪凯 马庆然
国家管网集团广东省管网有限公司
水合物生成引发的流动保障问题是制约油气开采、水合物开发和天然气长距离输送的重要因素[1]。目前,对水合物的抑制方法主要有传统控制法和风险控制法[2-3],传统控制法包括降压法、加热法和添加热力学抑制剂法,虽然可以一定程度上避免或延缓水合物的生成,但均存在一定局限性且成本耗费巨大;风险控制法通过在管道中加入少量的动力学抑制剂和阻聚剂,来延长水合物的生成和聚并过程,以此实现对输气管道的风险控制,是今后水合物抑制的发展趋势。以上措施的顺利实施均离不开对水合物相平衡即生成过程的研究,因此,研究水合物的生成机理及流动特性,对输气管道内水合物的生成概率进行分析显得尤为重要。
水合物的生成受成核驱动力、水相特性、外部扰动、气相组成和多孔介质等因素影响,且各因素具有显著的随机性,故水合物的生成也应具有不确定性[4-5]。从1950 年开始,有学者提出了采用可靠性设计的方法解决随机变量的不确定性,即以概率形式描述参数不确定性。Q/SY 06303.3—2019《油气储运工程线路设计规范第3部分:输气管道基于可靠性的设计和评价指南》中就对腐蚀管道剩余强度的可靠性进行了描述和验算,并已在管道强度设计和应力校核方面广泛应用[6-7]。借鉴以上标准的研究方法,基于水合物生成条件和过冷度的要求,建立水合物生成的极限状态方程,通过拉丁超立方抽样法对随机变量进行抽样,并采用蒙特卡洛方法对不同条件下的生成概率进行模拟,以期为提高输气管道流动保障安全提供实际参考。
1 水合物生成概率模型
基于随机性的水合物生成概率计算步骤如下:确定研究对象,建立极限状态方程;通过现场工况,统计各项参数,确定其服从的概率分布类型;采用超立方拉丁抽样对参数进行分组提取,代入极限状态方程中,计算水合物生成概率。
1.1 极限状态方程
水合物的生成受诸多因素影响,为实现计算的便捷性,在此只考虑对其影响最大的成核驱动力因素(包括温度、压力、过冷度、过饱和度等)。对于某一特定管道,天然气在输送过程中形成水合物的温度、压力是一一对应的,通过比较相同压力下管道天然气的流动温度与水合物的生成温度即可判定水合物是否生成。邓道明等[8]根据水合物的热力学特性建立了极限状态方程。但在水合物结晶成核之前,会有相当长的一段时间内,系统的宏观特性不会发生大的改变,即水合物在全面快速生长之前会有诱导期存在。延长水合物生成诱导期,可以避免水合物生成造成管道堵塞;缩短水合物生成诱导期,对于水合物浆液流动、制冷分离及天然气储存等方面具有重要意义[9]。在此,采用相同条件下水合物的实际生成温度与热力学预测得到的生成温度的差值即过冷度,作为衡量水合物生成诱导期的参数,建立极限状态方程,即式中:xi为管道沿线第i点;Ti为第i点的温度,℃;TH,Ti为在第i点的压力下水合物形成温度,℃;Ts为过冷度,℃。
Z0(xi)为评价基准函数:当Z0(xi)>0,表示第i点不会生成水合物;当Z0(xi)<0,表示第i点会生成水合物;当Z0(xi)=0,表示第i点在水合物的生成曲线上。
气体中只有存在饱和水或有游离水析出,水分子才能通过氢键形成笼形结构,进而生成水合物。目前,确定天然气饱和水的方法有图解法、实验法和状态方程法,其中状态方程法最为准确,故采用PR状态方程进行多组分的相平衡计算,进而求解天然气饱和水含量[10],并对公式(1)进行修正,即
式中:Z1(xi)为第i点的水合物状态;w(xi)为在第i点是否存在饱和水,存在取1,不存在取0。
1.2 拉丁超立方抽样
为了保证每个参数的随机抽样样本在空间内均匀分布,采用分层抽样中的拉丁超立方抽样法[11-12]。以m个不确定因素的组成集{x1,x2,…,xm} 为例进行分析,首先将单因素xi的取值空间按照等概率密度划分为n个连续区间;随后在每个区间中按照规则抽取一个样本,形成xi的样本空间为;随机排列xi的样本空间,对于因素集{ }x1,x2,…,xm,每次选择n列中的一行构成全因素样本集,将以上全因素样本集抽取n次后,得到n×m的样本矩阵,完成抽样过程。
1.3 蒙特卡洛模拟
蒙特卡洛模拟是基于大数定理和中心极限定理的概率求解方法,将经拉丁超立方抽样得到的数据代入公式(1),在公式(2)的约束条件下,考察Z0(xi)<0的出现概率,将其作为输气管道水合物的生成概率。
2 实例验证
以某输气管道为例进行分析,该管道全长60 km,管径711 mm×10 mm,管壁粗糙度0.015 mm,埋深1.5 m,地温5 ℃,总传热系数2 W/(m2·K),入口压力6 MPa,入口温度30 ℃,管输流量为80 kg/s。气质组分见表1,管道高程见图1,水合物生成的相平衡曲线和沿线温度、压力变化见图2,水合物生成的体积分数见图3。可见,随着管输距离的增加,沿线温度、压力不断下降,在55.8 km 处开始生成水合物,并在58.8 km 处达到峰值,为0.4%。
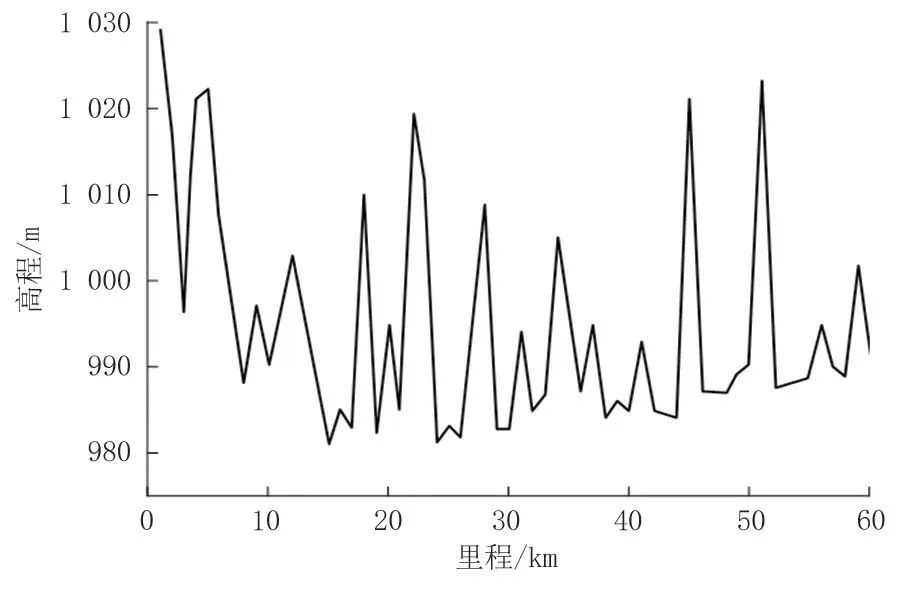
图1 沿线高程Fig.1 Elevation along the line
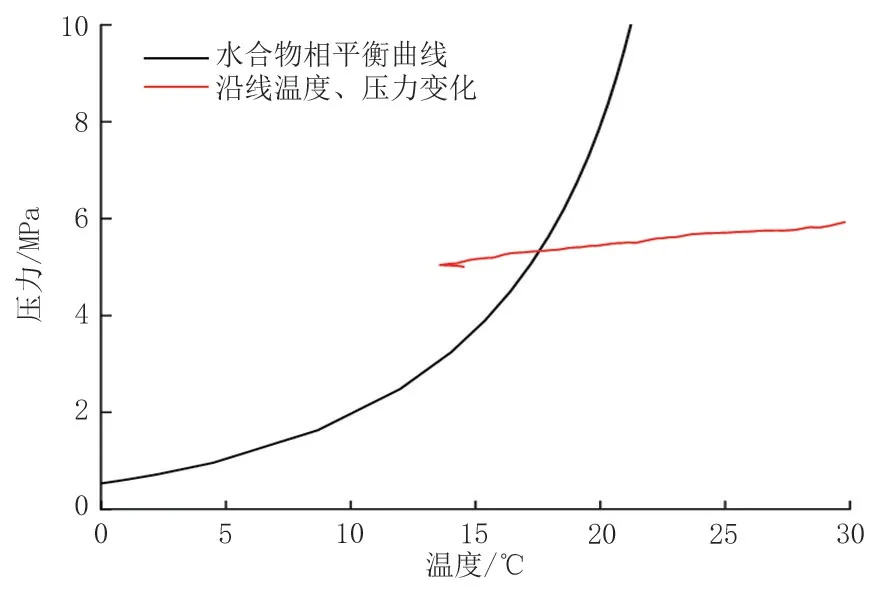
图2 沿线温度、压力变化Fig.2 Temperature and pressure changes along the line
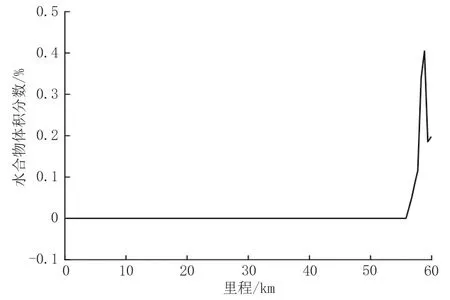
图3 水合物生成的体积分数Fig.3 Volume fraction of hydrate formation
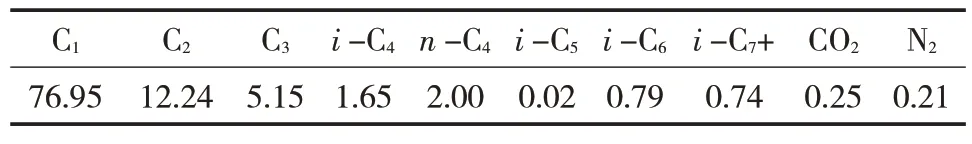
表1 气质组分Tab.1 Gas composition 摩尔分数/%
2.1 随机参数的不确定性分析
利用SCADA 系统,收集整理该输气管道运行过程中的实测数据,对其进行统计分析,得到温度、压力和流量的最佳分布模型,候选分布模型有正态、对数正态、Weibull、Gamma、指数等,采用样本分布函数与经验分布函数的AD(Anclerson-Darling)距离检验数据的符合程度,AD 统计量越小,表示分布模型越优,结果见表2。由表2 可知,温度、压力和流量分别在正态、正态和Beta分布时的拟合效果较好,分布模型分别为N(30,1)、N(6,1)、G(80,1.65,5.21)。其中,N 表示正态分布,两个参数依次为均值和标准差,G 表示Gamma分布,三个参数依次为位置、标度和形状。
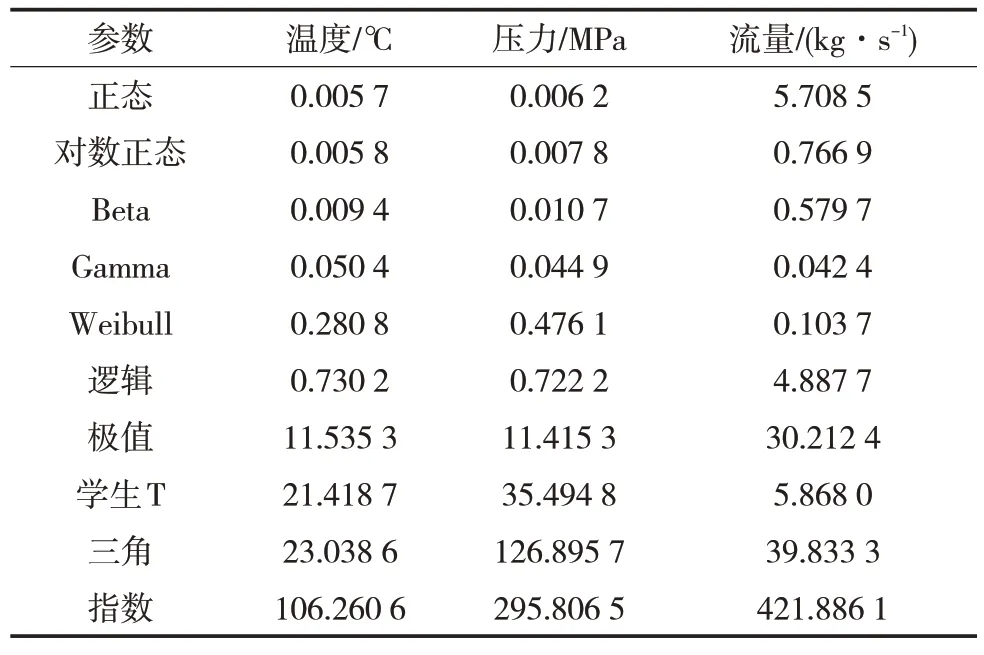
表2 随机参数的AD检验结果Tab.1 AD test results of random parameters
2.2 单参数对水合物生成概率的影响
在固定温度、压力和流量中任意两个参数后,计算单参数的不确定性对水合物生成概率的影响(图4)。当随机参数为温度时,管道在42 km 开始生成水合物,当拉丁超立方抽样的次数达到50 个以上时,生成概率趋于平滑,基本不再变化,没有凸起或凹陷的平台区产生,这与热力学预测方法中的水合物在连续管段中持续生成的结论相符。当随机参数为压力时,管道在35 km 开始生成水合物,当样本数量在100 个以上时,生成概率趋于平缓。当随机参数为流量时,管道在48 km开始生成水合物,除样本数量10 以外,其余样本数量对流量的敏感性不强。综上所述,当样本数量大于100 时,抽样次数对水合物形成概率的影响趋于稳定,从生成水合物的区域敏感性分析,入口压力的影响最大,其次为入口温度和入口流量。
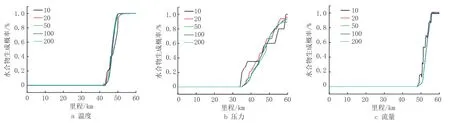
图4 单参数对水合物生成概率的影响Fig.4 Influence of single parameter on probability of hydrate formation
2.3 多参数对水合物生成概率的影响
在样本数量足够的前提下,分别考虑双参数和三参数的不确定性对水合物生成概率的影响(图5)。可见多参数与单参数对水合物的生成概率影响截然不同,考虑压力与同时考虑压力和流量的生成曲线类似,考虑温度与同时考虑温度和流量的生成曲线类似,同时考虑温度和压力的水合物生成区域较其余双参数均靠前。此外,三参数的水合物生成区域最靠前,但生成概率有所下降,说明随机变量越多,全线水合物形成的可能性越大。
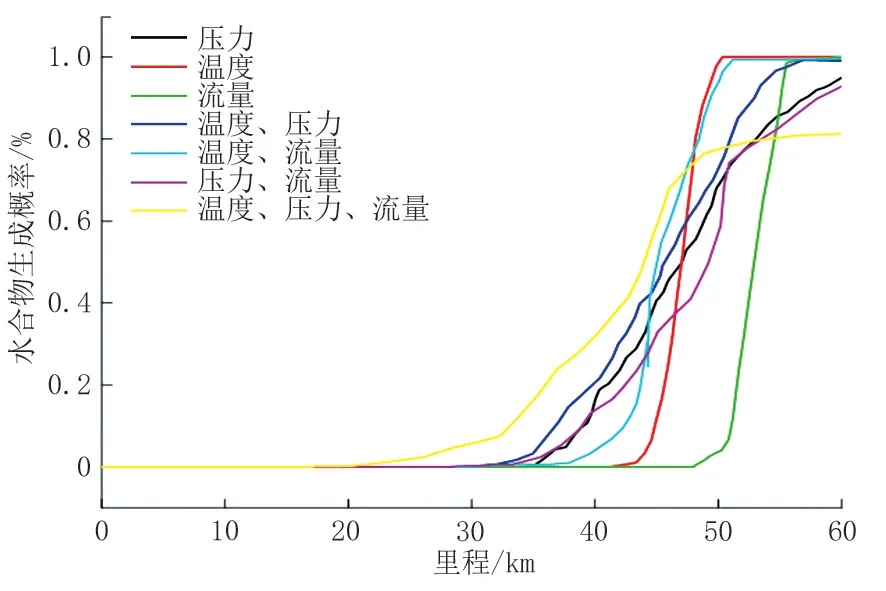
图5 多参数对水合物生成概率的影响Fig.5 Influence of multiple parameters on the probability of hydrate formation
2.4 参数统计量对水合物生成概率的影响
针对2.1 中给出的参数分布类型,考虑不同统计量对水合物生成概率的影响(图6)。随着温度的均值下降、压力的均值上升,水合物的生成概率迅速上升,生成区域不断靠前,且这种趋势逐渐增大,鉴于这两个参数属于正态分布,故应合理控制两者的均值,避免温度、压力的上下波动,降低波动的标准差,将正态分布收窄,对于降低水合物生成风险具有重要意义。随着流量的位置参数增大,水合物的生成区域向后移动,但这种趋势逐渐减小,说明达到满管流量后,流速基本保持不变,此时对水合物生成起驱动作用的压力保持平衡状态,对水合物的生成不构成影响。
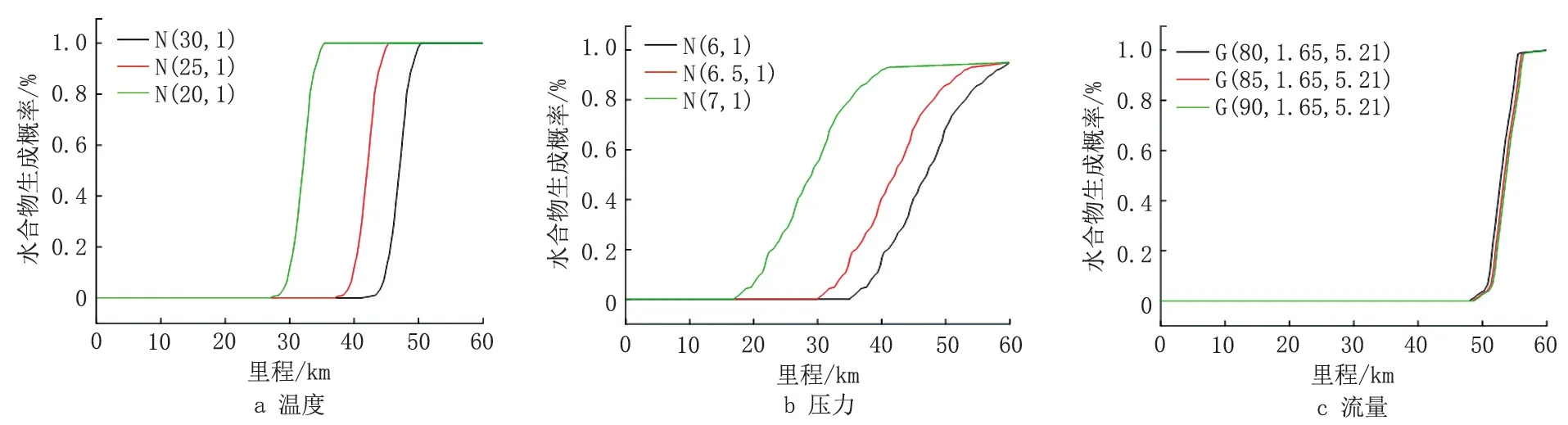
图6 参数统计量对水合物生成概率的影响Fig.6 Influence of parameter statistics on hydrate formation probability
3 结论
(1)通过AD 检验结果可知,温度、压力和流量分别在正态、正态和Beta 分布时的拟合效果较好,体现了参数的随机性和不确定性。
(2)当样本个数大于100时,抽样次数对水合物形成概率的影响趋于稳定,从生成水合物的区域敏感性分析,入口压力的影响最大,其次为入口温度和入口流量。
(3)随机参数越多,全线水合物的形成风险越大;温度、压力均值的变化对水合物生成概率的影响较大,流量位置参数的变化对生成概率的影响有限。
