回归分析对比GRA探究底板破坏深度影响因素的研究

2023-06-17朱进鹏余照阳

能源新观察 2023年2期

朱进鹏余照阳

摘要：为探究矿井底板破坏深度的影响因素及其影响关系，各因素之间的复合相关性分析常用的方法有灰色关联法（GRA）和相关分析，回归分析是相关分析中的一个分支。灰色关联分析在分析灰色数据中的线性关联程度等方面应用非常广泛，但对于数据完整且充足的情况，灰色关联分析在处理数据后使数据损失了大量有用信息；本文借助相关分析和回归分析结合使用分析数据之间的关联性（包括非线性关联），利用回归方程进行预测并对其进行显著性检验以及进行方差分析，在张文泉等人利用灰色关联研究影响底板破坏深度的因素的基础上，利用多元统计建立了新的选回归模型，对模型进行了显著性检验以及方差分析，该模型预测表现良好并可应用于实际生产中，该方法是对研究底板破坏深度的新补充，并可迁移运用于其他相关领域，且回归方程将随样本量的增加而更加精确。

關键词：回归分析 GRA 底板破坏深度影响研究

煤层底板的破坏因素分析数据之间的关联性目前已有许多方法，在工业、农业、管理等实际项目中灰色关联分析与回归分析是工程实际中最为常用的方法，灰色关联分析的产生基于灰色系统，适用于快速分析数据关联性，同时也存在一些无法避免的缺陷；回归分析相较与灰色关联分析较为复杂，但能够有效的弥补灰色关联分析存在的不足，在建立了显著的回归模型之后，合理利用该模型，可在实际生产中进行应用预测并取得良好效果。

1、选用回归分析的依据

灰色关联分析[1]（以下简称GRA），是谭学瑞等教授于1995年提出的多因素统计新方法，其理论基础是基于邓聚龙教授灰色系统理论[2]。利用GRO来描述因素间关系的相互影响的强弱关系、大小关系、次序关系等。基本思想是以主要研究对象的数据列作为参考依据，采用简单的数学关系来研究各个因素相对于主要研究对象数据的对应关系[3]。能够在一定层面上体现指标的动态变化，在量化分析上体现了一定的动态意义。目前在医药卫生、农业、工业、管理等方面应用较为广泛。

灰色关联分析核心思想是将数据无量纲化后构建差序列，并以最大差和最小差构建如下公式

式中，为母序列，计算出母序列与每一个子序列的关联度系数，对该序列的关联度取平均，即得该序列与主序列之间的关联度

灰色关联分析的优点与不足：近年来，灰色关联虽然得到了广泛的应用，但没有得到持续的发展，许多学者在白色系统上应用灰色关联法，以简化计算相关的复杂统计计算，张文泉[4]等人将其用于分析影响底板破坏深度的影响因素研究。该方法的无量纲化的数据处理会不同程度的导致原始数据的描述性、峰值和正负性等信息损失，尤其初值法具有很大的风险，当初值为噪音的时候，得到的关联度结果往往都大于0.5，其结果也只能大致判定关联程度的大小，没有显著的区分度以及正负相关的区分能力，且对于结果的正确性缺乏必要的检验，此方法还有待进一步研究。下面从回归分析的角度重新研究影响底板破坏深度的因素。

2 、利用选回归模型探究影响底板破坏深度的因素

2.1 回归分析建模

从19世纪初Gauss提出最小二乘法算起，回归分析已有200多年的历史，其在生产实践中的广泛应用是回归分析不断自我发展和完善的根本动力[5]。回归分析研究的主要对象是客观事物变量间的相关关系或回归关系，回归关系和相关关系是现代统计学中关于统计关系的研究形成的两个重要分支。回归分析相较与相关分析不仅可以刻画变量间的线性相关的密切程度，还可以揭示变量对变量的影响大小，回归模型建立检验后还可以服务于预测和控制，因而在生产实践中具有更加重要的意义[6、7]。

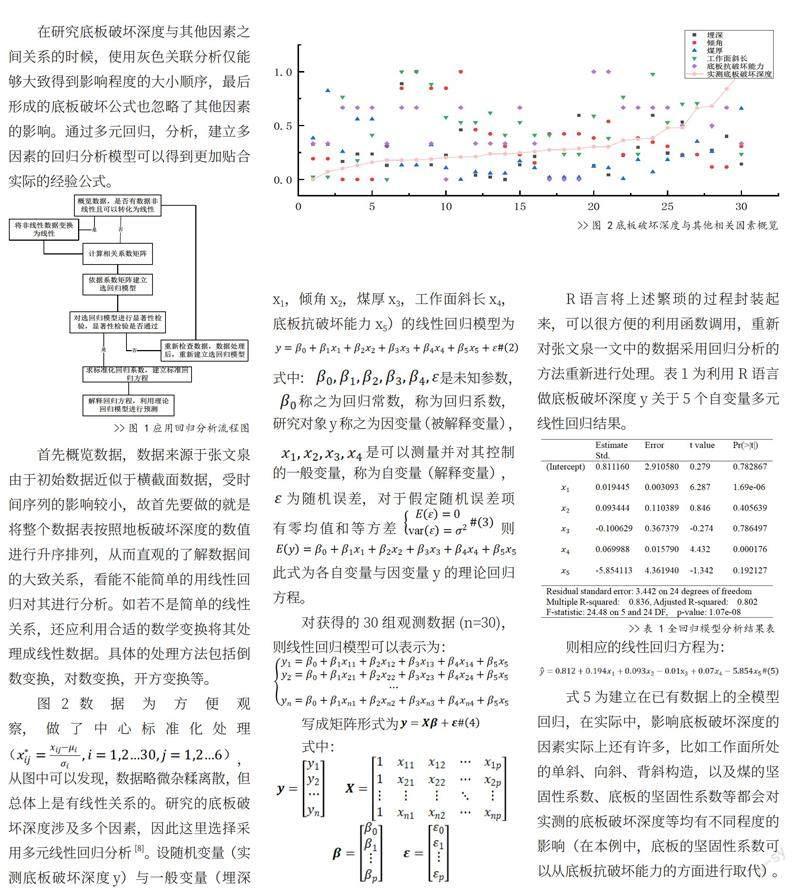
在研究底板破坏深度与其他因素之间关系的时候，使用灰色关联分析仅能够大致得到影响程度的大小顺序，最后形成的底板破坏公式也忽略了其他因素的影响。通过多元回归，分析，建立多因素的回归分析模型可以得到更加贴合实际的经验公式。

首先概览数据，数据来源于张文泉由于初始数据近似于横截面数据，受时间序列的影响较小，故首先要做的就是将整个数据表按照地板破坏深度的数值进行升序排列，从而直观的了解数据间的大致关系，看能不能简单的用线性回归对其进行分析。如若不是简单的线性关系，还应利用合适的数学变换将其处理成线性数据。具体的处理方法包括倒数变换，对数变换，开方变换等。

图2数据为方便观察，做了中心标准化处理，从图中可以发现，数据略微杂糅离散，但总体上是有线性关系的。研究的底板破坏深度涉及多个因素，因此这里选择采用多元线性回归分析[8]。设随机变量（实测底板破坏深度y）与一般变量（埋深x1，倾角x2，煤厚x3，工作面斜长x4，底板抗破坏能力x5）的线性回归模型为式中：是未知参数，称之为回归常数，称为回归系数，研究对象y称之为因变量（被解释变量），是可以测量并对其控制的一般变量，称为自变量（解释变量），为随机误差，对于假定随机误差项有零均值和等方差则此式为各自变量与因变量y的理论回归方程。

对获得的30组观测数据（n=30），则线性回归模型可以表示为：

写成矩阵形式为

式中：

R语言将上述繁琐的过程封装起来，可以很方便的利用函数调用，重新对张文泉一文中的数据采用回归分析的方法重新进行处理。表1为利用R语言做底板破坏深度y关于5个自变量多元线性回归结果。

则相应的线性回归方程为：

式5为建立在已有数据上的全模型回归，在实际中，影响底板破坏深度的因素实际上还有许多，比如工作面所处的单斜、向斜、背斜构造，以及煤的坚固性系数、底板的坚固性系数等都会对实测的底板破坏深度等均有不同程度的影响（在本例中，底板的坚固性系数可以从底板抗破坏能力的方面进行取代）。从值F=24.48相较于24（F分布的自由度）可知，显著性并不明显，这是由于部分因素没有与底板破坏深度显著相关，下面利用相关系数剔除明显不相关的因素[9]。各因素之间的相关系数矩阵如下表所示：

根据表2相关系数表中与各自变量之间的关系，可以发现采厚对底板破坏深度几乎没有关联，将其剔除，进一步利用R语言建立选回归模型，模型结果如表5所示：

由表3可知，剔除后的选回归模型为：

决定系数，由决定系数可以看出回归方程是显著的。方程整体显著性检验，，表明回归方程是显著的。这与工程中的实际经验相符，底板破坏深度与埋深、倾角、工作面斜长均呈现正相关关系，与底板抗破坏强度呈现出负相关关系，各回归系数的值不能够仅凭数值大小来判定哪个因素的影响更大或者更小。回归模型的具体解释为：当保持不变时，为一常数，则有：

即可解释为在除开之外的因素保持不变时，每增加一个单位，即为y的平均增加幅度，，埋深每增加1米底板破坏深度平均增加0.019米，埋深增加100米时，底板破坏深度平均增加幅度为1.9米。

2.2 对回归方程做显著性检验

为观察自变量x从整体上对随機变量y是否产生了明显的影响，利用F检验，提出原假设H0

若没有足够的理由拒绝H0，则说明随机变量y与自变量x之间的关系不适合用线性回归模型表示，利用总离差平方和的分解式[10]

简写为

构造F检验统计量[11]

在正态假设下，当原假设，成立，F服从自由度为的F分布，在本例中，n=30，p=4，取显著性水平，在上述选模型中，F值=31.75，对应的P值为，由此可判断，选回归模型的回归方程在整体上是显著的，即做出这4个自变量整体对因变量产生的显著线性影响的判断所犯错误的概率是极低的。

2.3 对线性回归方程做方差分析

利用R语言将方差分析具体到每个自变量，并通过P值可以看出每个自变量y对因变量是否产生显著的影响，从上述结果看出，在回归方程中，x1和x4相较x2和x4产生较为显著的影响（显著性水平），这与回归方程整体的显著性检验是一致的[12]。

2.4 中心化和标准化求出标准化回归系数

在多元线性回归分析中，因涉及多个变量，自变量的单位和数量级往往不同，给进行结构分析带来一定的困难，数据量级悬殊过大会导致出现较大误差。故在进行结构分析时，需要对数据进行如下处理

中心化：

标准化：

利用R语言中的QuantPsyc包，使用lm.beta（）即可得到各因素的标准化回归系数如下：

相应的标准化回归方程为：

从标准化回归系数可以看出对y影响最大的因素是x1，其次是x2，表示底板破坏深度每增加1%，埋深会平均增加0.6163%，倾角会增加0.1%，工作面斜长增加0.455%，而底板抗破坏能力会降低0.13%，因为自变量是客观存在的，这样的解释在实际中是行不通的，因此只能作为判断的依据，实际预测必须采用理论回归方程[13]。

2.5 应用理论回归方程做出预测

在张文泉拟合的底板破坏公式中，在分析误差的时候，不应利用原始数据推导出的拟合公式去预测与原始数据的误差，得到的误差也只是基于拟合公式的自拟合度。利用其去预测其他数据则会产生过拟合现象，导致误差扩大，而应利用新的数据去做预测来验证模型的可靠性。笔者在施龙青等人基于GWO改进的PCA-BP神经网络预测模型的数据中应用多元回归模型，得到表6。

由表6可以看到，30个煤矿预测的平均相对误差为21.7%，这与其他方法所建立的模型误差基本一致，因为还有诸如构造、水压等因素影响底板破坏深度，故这个误差是完全可以接受的。30个煤矿预测的平均绝对误差仅为-0.31m，虽然每个煤矿的地质、开采等条件不一样，但还是基本符合所建立的选回归模型，说明模型的效果是非常贴合实际的。

3 、总结

1.灰色关联算法简单，便于计算，但区分度不够显著且不能用于非线性数据，适合用于数据的初步判断和观测，在预测煤层低板深度时不能够深入分析各元素之间的相关程度。

2.回归分析可以有效弥补灰色关联的缺点，结合相关分析可以筛选出影响因素中主要相关因素，对数据采用非线性变换还可应用于非线性数据，从而构建具有较高显著性的选回归模型，从各角度揭示了埋深、倾角、工作面斜长等因素对于底板深度的影响程度。且模型应用较为简单，便于应用到实际预测和验证中。

3.在绘制简单折线图时，底板破坏深度随埋深的震荡现象不能排除是由周期性的影响，由于样本量不足，需要进一步的研究。

参考文献

[1] 刘思峰，蔡华，杨英杰等。灰色关联分析模型研究进展[J]。系统工程理论与实践， 2013， 33（8）： 2041-2046。

[2] 邓聚龙。灰色系统理论简介[J]。内蒙古电力， 1993（3）： 51-52。

[3] 熊远南。基于改进灰色-多元回归组合预测模型的燃煤电厂智慧水务研究[J]。化工进展， 2020， 39（S2）： 393-400。

[4] 张文泉，赵凯，张贵彬等。基于灰色关联度分析理论的底板破坏深度预测[J]。煤炭学报， 2015， 40（S1）： 53-59。

[5] 何晓群。应用回归分析：R语言版。[M]。电子工业出版社， 2017。

[6] 卫星君，赵晓萌，马长玲等。降雨型滑坡灾害的约简和逻辑回归预测模型[J]。中国安全科学学报， 2018， 28（8）： 1-6。

[7] 汤轶雄，徐传玲，文超等。高铁故障晚点时间预测的支持向量回归模型[J]。中国安全科学学报， 2019， 29（S2）： 18-23。