压缩空气泡沫在长距离管路输送中压降的数值模拟

张佳庆,黄 勇,周亦夫,过 羿,黎昌海,黄玉彪

(1.国网安徽省电力有限公司电力科学研究院,合肥,230601;2.电力火灾与安全防护安徽省重点实验室,合肥,230022;3.国家电网公司输变电设施火灾防护实验室,合肥,230022;4.国家电网有限公司,北京,100031;5.中国科学技术大学火灾科学国家重点实验室,合肥,230026)

0 引言

特高压直流输电技术凭借其输电距离远、输电容量大、电能耗损小等特点已在国内得到广泛应用。然而特高压变压器等充油设备一旦发生火灾,火势发展迅猛,火灾规模大,传统水喷雾灭火系统无法达到有效灭火的目的。

压缩空气泡沫灭火系统,简称CAFS,是将一定比例的压缩空气引入加压泡沫混合物中,混合后产生灭火泡沫,然后通过管道输出。由于其较好的灭火性能且能有效扑救B类火灾[1,2],已广泛应用于特高压变压器等特殊灭火场景中。CAFS的灭火效率比常见的水灭火系统高10倍以上[3],且泡沫在前端主机部分产生,在火灾中受高温、烟气、爆燃等不利因素影响较小。同时,压缩空气泡沫灭火系统可以将压缩空气泡沫进行远距离输送,避免了爆炸损毁的问题,压缩空气泡沫在长距离管路输送中压降的研究,利于预测管道与消防炮连接端的压力值,达到超远距离灭火。

目前,国内外如对压缩空气泡沫在管内的流动特性已有部分研究,如陈旸等[4]对压缩空气泡沫在管网中的输送进行了实验研究,探讨了泡沫输送流量对管道摩擦阻力损失的影响,发现在泡沫输送过程中,管道内的压力和压力损失随着泡沫流量的增加而增加。此外,压缩空气泡沫在管道内流动的数值模拟大都集中于100 m以内距离[5,6]的管道。林全生等[5]对压缩空气泡沫在短距离管道中的流动进行了数值模拟,研究发现管路的出口压力随着流量增大而增加,同时在不同的测压点也具有相同的趋势。

以上研究主要针对短距离管道内压缩空气泡沫的输送特性,对长距离管道中压缩空气泡沫输送的研究较少。徐学军[7]进行了大量全尺寸实验,对AFFF压缩空气泡沫在实际消防管网中的流动特性进行了研究,开展了压缩空气泡沫在1 000 m超长水平管道内输运的实体实验,分析典型因素对管网压力衰减的影响。

然而对压缩空气泡沫在100 m以上的长距离管路输送中的压降数值模拟研究相对较少,且管长、管径等对长距离管道内压降的影响需要进一步探究。

因此,基于Fluent软件,本文对400 m长距离管道中压缩空气泡沫的流动特性进行了数值模拟,并分析了管道直径尺寸对压降变化的影响,探讨了不同AFFF压缩空气泡沫原液浓度对管内流动影响的规律。

1 数值模拟计算方法

1.1 几何模型与网格划分

选择直径分别为50 mm、65 mm和80 mm的管道模型,管道长度尺寸均为400 m,如图1所示。采用Gambit软件对其进行网格划分,其中为了符合黏性影响区流体流动求解要求,将壁面的网格进行加密[8],如图2所示。

图1 管道物理模型示意图Fig.1 Schematic diagram of the pipeline physical model

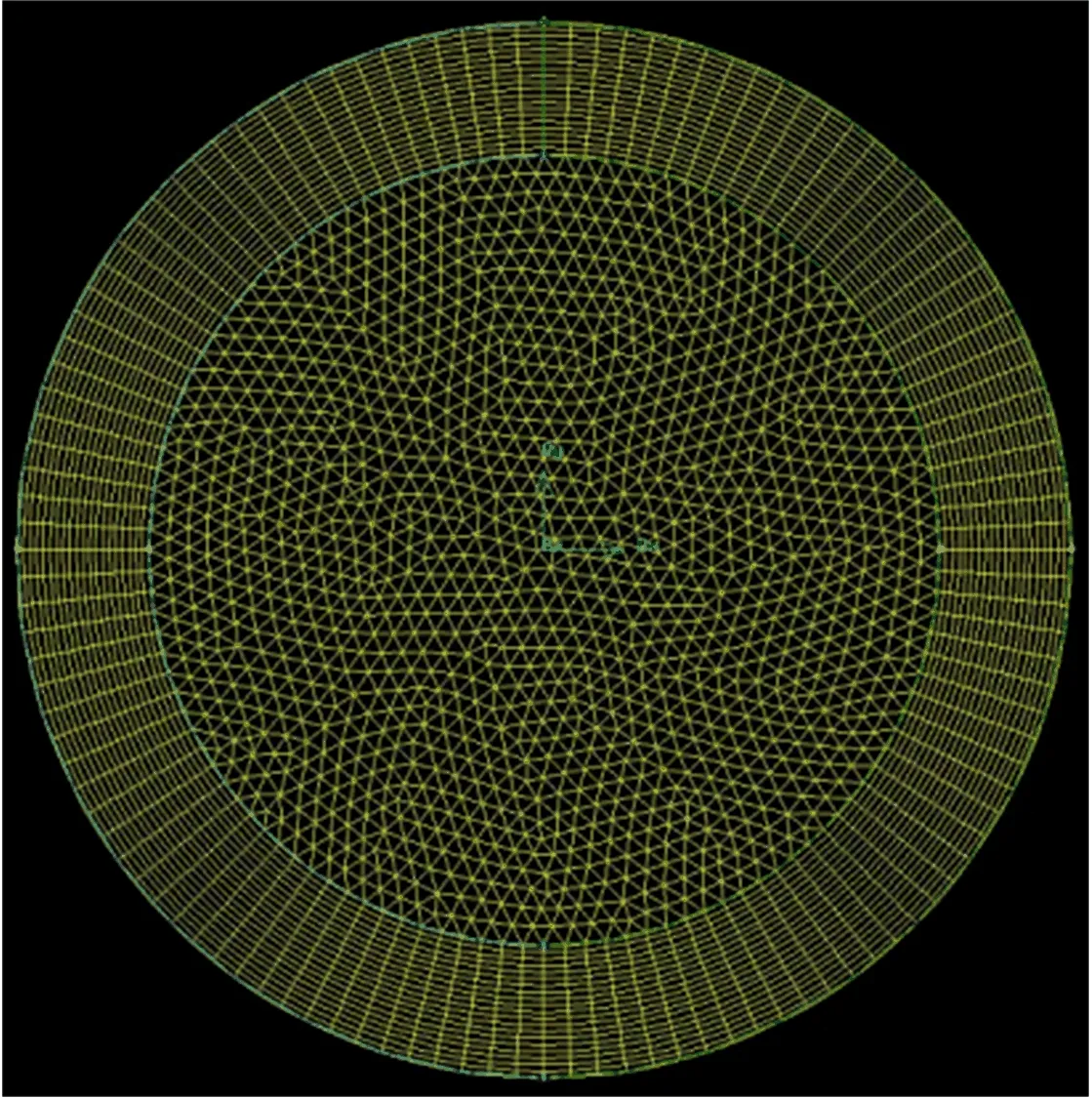
图2 几何模型网格划分Fig.2 Mesh division of geometric model

1.2 网格无关性验证

对管道压降进行数值模拟前,首先进行了网格无关性验证,如图3所示。随着网格数量的增加,400万网格之后,压降几乎不再变化。本文中选用600万网格量进行数值计算。

图3 网格数量的无关性验证 Fig.3 Grid independence verification

1.3 数学模型

文献[7]的实验中,泡沫液的流量控制为400 L/min,压缩空气泡沫流速较快,大都为湍流形式。在本文中,选择了Spalart-Allmaras(S-A)模型来模拟管道内泡沫的流动,该模型适用于雷诺数较低的湍流状态[5]。计算选用SIMPLE算法。

基本控制方法包括连续性方程、动量方程和S-A方程。

连续性方程为：

(1)

式中,ρ——流体密度,kg/m3;

t——时间,s;

vx——x方向的流体流动速度,m/s;

vy——y方向的流体流动速度,m/s。

动量方程为：

(2)

式中,p——流体流动静压,Pa;

ui,uj——速度张量,m/s;

τij——应力张量,Pa;

ρgi——i方向上重力体积力,N;

Fi——i方向上外部体积力,N;

xi,xj——坐标张量。

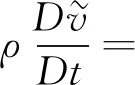
(3)

Y——壁面阻挡和黏性阻尼产生的湍流粘性的减少项,kg/(m3·s);

G——湍流黏性产生项,kg/(m3·s)。

1.4 边界条件的设定

管道模型的入口为速度进口,用AFFF泡沫的流量值进行速度换算,流量为400 L/min,入口压力为1 MPa,管道的出口为压力出口。壁面的边界条件设为无滑移边界条件。

1.5 管道截面的建立

分别在长输管道的100 m、200 m、232 m、300 m和400 m处建立截面,获得截面处压力,以此探求压缩空气泡沫在长输管道内的压降变化特性。

2 流形的假设

泡沫灭火剂根据泡沫浓缩物的不同成分可分为蛋白质型和合成型[9,10],本文选用合成型的AFFF泡沫,其具有灭火效率高和封闭性能好等优点。

经过发泡处理后的气泡含气量大于80%,泡沫形态类似弥散流[11],因为管道内的泡沫流动是充分发展的,将其简化作单相流进行计算。材料类型采用表观粘度进行表征,采用Herschel-Bulkley模型计算泡沫的表观黏性系数[12]。计算方法如式(4)所示。

(4)

式中,τ0——剪切速率为零时的剪切应力,Pa;

γ——剪切速率,s-1;

K——流变系数。

其中,由文献[13]可得,参数γ取150 s-1。采用Balmforth等[14]定义屈服应力的方法,得到泡沫的屈服应力τ0为 1.5 Pa,并通过拟合剪切应力和剪切应变实验值得到参数K=1.19,n=0.383,由此可得泡沫表观粘度为0.064 Pa·s。

压缩空气泡沫系统选用设备为T5固定式压缩空气泡沫系统,系统可以产生不同气液比类型的压缩空气泡沫,气液比的大小通过对泡沫混合液流量与空气流量的比例进行控制。在本文研究压缩空气泡沫的流动特性时,均设定气液比为6∶1。

3 结果分析与讨论

3.1 长输管道内压降变化特性

对不同截面处的压降进行分析,管道中压降伴随距离的变化如图4所示。随着距离的增加,管道内压降均呈现线性变化,且随着压缩空气泡沫的流动,压降线性增大。以管径80 mm的管道为例,压缩空气泡沫流动到100 m处时,其压降为36 kPa,随着流动的进行,当输送距离达到232 m时,其压降变为97 kPa。400 m处的压力最小,压降进一步增加,达到146 kPa。

图4 管道内压降随距离的变化Fig.4 Variation of pressure drop in tube with distance

将各管道模型的压降进行线性拟合,得到压缩空气泡沫压降拟合曲线方程为：

ΔP1=k1m

(5)

式中,ΔP1——压缩空气泡沫压降,kPa;

k1——压缩空气泡沫平均单位长度压降,kPa;

m——管道长度,m。

压降随距离变化的拟合曲线方程如表1所示,不同管径的管道压降随距离的增加均呈现线性增大。

表1 压降拟合曲线方程Table 1 Pressure drop fitting curve equation

压降拟合曲线的斜率为平均单位长度压降k1,其表示距离增加对压降增大的影响程度。随着距离的增加,不同管径大小的管道压降均呈现线性增大。且管径大小影响平均单位长度压降k1,从表2可以看出,管道直径越大,平均单位长度压降k1越小,即距离对压降的影响程度越小。

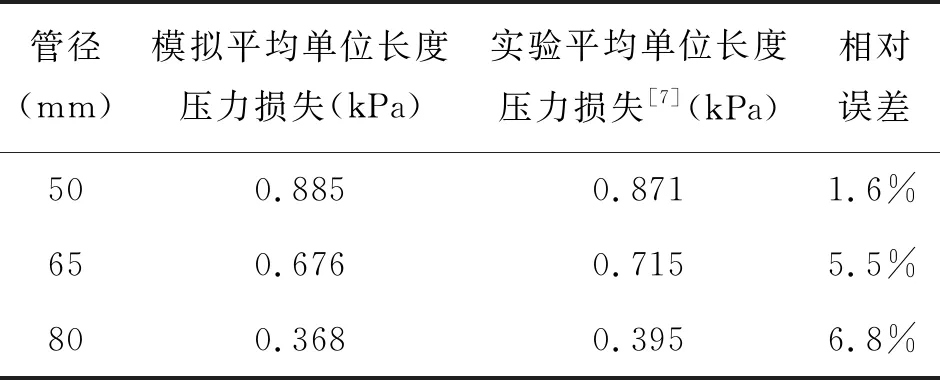
表2 平均单位长度压力损失Table 2 Average unit length pressure drop

当压缩空气泡沫在管内流动时,管径50 mm的管道,平均单位长度压降最大,为0.885 kPa/m,实验值为0.871 kPa/m;管径65 mm的管道,平均单位长度压降为0.676 kPa/m,实验值为0.715 kPa/m;管径80 mm的管道,平均单位长度压降为0.368 kPa/m,实验值为0.395 kPa/m,平均单位长度压降误差均小于10%,在误差允许范围内。

3.2 管径对出口压力及压降的影响

压降随管径的变化如图5所示。随着管径的增大,相同距离处的压降均呈现线性下降趋势,以距离入口100 m处的位置为例,50 mm管径的压降为85 kPa,当管径增加至65 mm时,其压降变为63 kPa,管径增加至80 mm时,压降进一步降低为36 kPa。

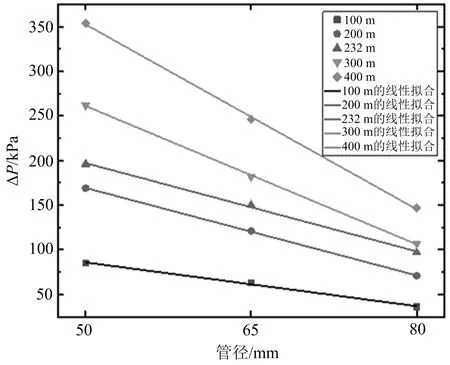
图5 不同管径压降随距离的变化Fig.5 Variation of pressure drop with distance for different pipe diameters

管径直接影响管内的压力分布和压降大小。随着距离的增加,管径增大对压缩空气泡沫压降降低的影响更为明显。在100 m处,选用65 mm管径比选用50 mm管径,压降低22 kPa,在距离200 m处,选用65 mm 管径比选用50 mm管径,压降低48 kPa,而当距离提高到400 m时,65 mm管径的压降比50 mm管径的压降低80 kPa。因此,当压缩空气泡沫在短距离管道中流动时,管道直径对压降的影响很小,当压缩空气泡沫在长距离管道中流动时,选择较大的管道直径可以显著降低压降。

为体现管径对压降的影响,通过改变管径大小,将不同距离处的压降进行线性拟合,得到压缩空气泡沫压降拟合曲线方程为：

ΔP2=-k2d+b

(6)

式中,ΔP2——压缩空气泡沫压降,kPa;

k2——压缩空气泡沫平均单位管径压降,kPa;

d——管径宽度,mm;

b——截距,m。

压降随管径变化的拟合曲线方程如表3所示。从表3中可以发现,在不同管长位置,压降随着管径的增大均呈现线性减小。

表3 压降拟合曲线方程Table 3 Pressure drop fitting curve equation

平均单位管径压力损失k2决定管径对压降的影响程度。管道越长,压缩空气泡沫平均单位管径压力损失越大,管长100 m处的平均单位管径压降为1.633 kPa,管长400 m处的平均单位管径压降为6.934 kPa,是管长100 m的4倍,在长距离管道中选用较大管径可以有效减小压降。

为验证模拟结果的可靠性,将不同位置处的模拟数据与文献[7]中的实验结果进行对比,同时进行误差分析。

将文献[7]中距离入口232 m处的实验结果与模拟数据进行对比,如图6所示。实验中管径50 mm的管道,压降为185 kPa,本文模拟值为196 kPa,压降误差为11 kPa。实验中管径65 mm的管道,压降为151 kPa,本文模拟值为150 kPa,压降误差为1 kPa。实验中管径80 mm的管道,压降为100 kPa,本文模拟值为97 kPa,压降误差为3 kPa。误差均在10%以内,在合理范围,进而验证了模拟的可靠性。

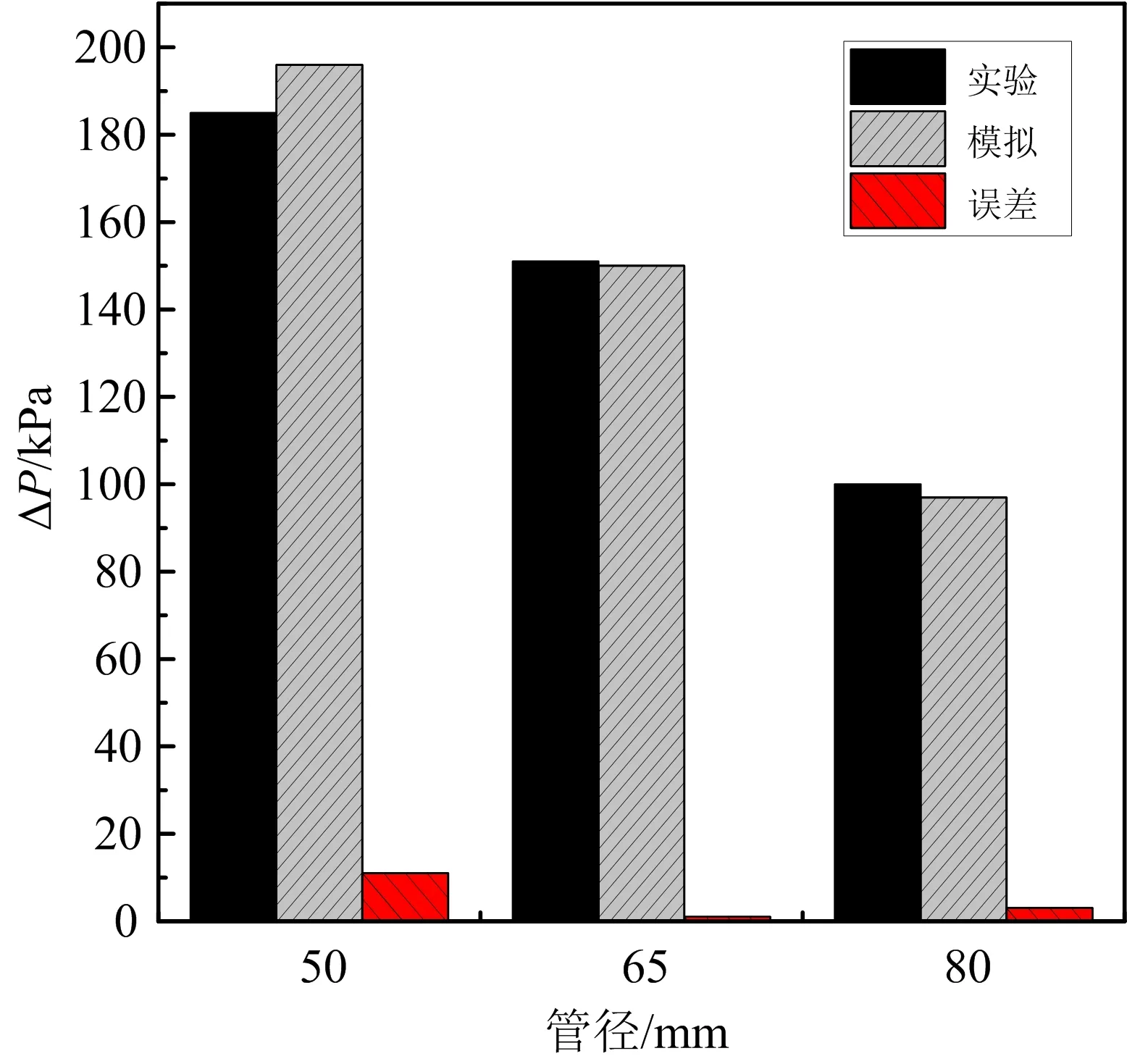
图6 距离入口232 m处的压降对比Fig.6 Pressure drop comparison at 232 m from the inlet

相应的,将模拟400 m处的压降结果与文献[7]的实验数据进行比较,结果如图7所示。实验中管径50 mm的管道,压降为350 kPa,本文模拟值为354 kPa,压降误差为4 kPa。实验中管径65 mm的管道,压降为275 kPa,本文模拟值为274 kPa,压降误差为1 kPa。实验中管径80 mm的管道,压降值为155 kPa,本文模拟值为146 kPa,压降误差为9 kPa。误差均在10%以内,验证了模拟结果的可靠性。

图7 距离入口400 m处的压降对比Fig.7 Pressure drop comparison at 400 m from the inlet

3.3 泡沫原液浓度对管内传输压降的影响

以文献[7]中的实验工况为依据,测定未经发泡的AFFF泡沫原液浓度对管内传输压降的影响,泡沫浓缩液所占的体积比为稀释比[12]。经稀释过的3%水成膜泡沫密度为1 010 kg/m3,粘度为18.7 cp,泡沫原液在管道内的流动同样按照单相流进行数值模拟计算。

从图8可以看出,在相同管道直径的情况下,1%浓度的AFFF泡沫原液和3%浓度的AFFF泡沫原液压降随距离的变化几乎没有差别,压降均呈线性变化。

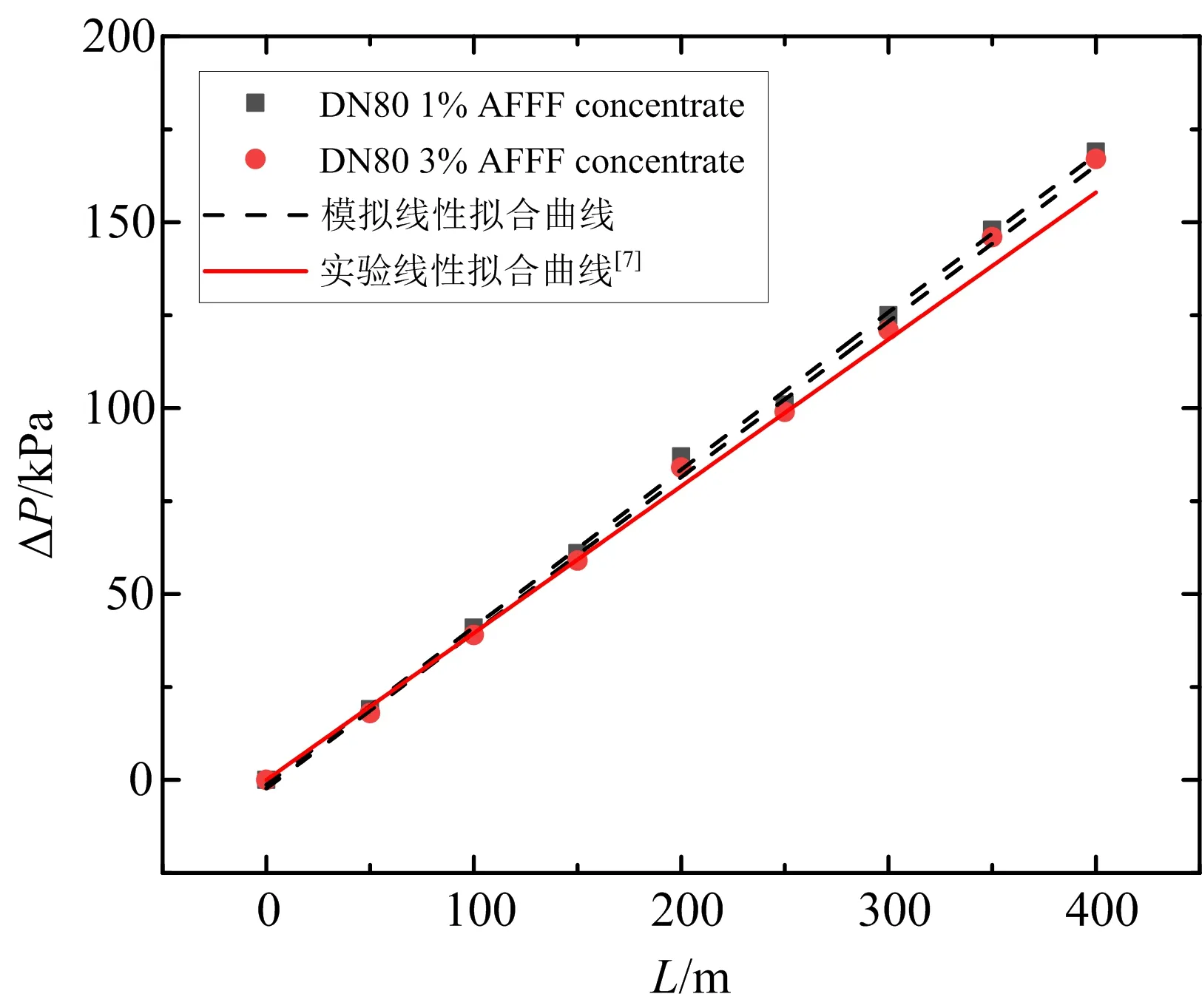
图8 不同浓度泡沫原液压降随距离的变化Fig.8 Variation of pressure drop with different distances of foam original solution with different concentrations

为直观表达泡沫原液在管道内压降的变化,将泡沫原液压降进行线性拟合,拟合曲线方程为：

ΔP3=k3m

(7)

式中,ΔP3——泡沫原液压降,kPa;

k3——泡沫原液平均单位长度压降,kPa/m;

m——管道长度,m。

不同浓度的泡沫原液压降随距离变化的拟合曲线方程如表4所示。可以看出,1%与3%浓度的泡沫原液平均单位长度压降k3仅相差0.01 kPa/m,泡沫原液浓度对泡沫原液平均单位长度压降几乎没有影响。

表4 压降拟合曲线方程Table 4 Pressure drop fitting curve equations

泡沫原液浓度对管道内压降几乎没有影响,如图9所示。1%和3%浓度的AFFF泡沫原液模拟压降分别为148 kPa和146 kPa,相差2 kPa。将文献[7]中距离入口350 m处测得的泡沫原液压降结果与模拟数据进行对比,1%浓度的AFFF泡沫原液误差值为2 kPa,3%浓度的AFFF泡沫原液误差值为5 kPa,误差在10%内,在允许范围内。

图9 距离入口350 m处泡沫原液压降对比Fig.9 Pressure drop comparison of foam original solution at 350 m from the inlet

泡沫原液浓度对管道内压降影响很小,而当流量一定时,压降与压缩空气泡沫系统中设置的泡沫混合液供给流量以及空气供给流量的比值有关,即与压缩空气泡沫的气液比相关。

4 结论

对压缩空气泡沫在管道内流动进行了数值模拟,并结合文献实验数据对比,对管道内各处的压力变化及压降变化特性进行分析,得到如下结论：

(1)在定气液比与定流量的情况下,400 m长管道内压缩空气泡沫的压降随着距离的增加而线性增加,且50 mm、65 mm和80 mm管径的管道单位长度压降分别为0.885 kPa/m,0.676 kPa/m和0.368 kPa/m。数值模拟结果与文献实验数据吻合良好,利用数值模拟压缩空气泡沫输送在长管道内的压降对工程设计计算具有一定的参考价值。

(2)在定气液比与定流量的情况下,管道直径对压缩空气泡沫压降影响显著,管径越大,压降变化越小。管道长度越长,平均单位管径压降k2越大,管径对压降的影响程度就越强烈。因此,在实际工程中,为使得管道末端有更大的压力输出,应综合选择管径和管长的大小,尽可能设置较短的输送管道并在输送时间允许的范围内,选择较大直径的输送管道。

(3)未经发泡的泡沫原液浓度对泡沫原液的压降变化影响不大,压降与压缩空气泡沫的气液比有关,长距离管道压降的工程计算中可忽略泡沫原液浓度的影响,重点考虑气液比因素。