基于栅格遗传算法的采购供应物流配送车辆路线规划方法

张大威，张明广，刘文浩，彭 振 （重庆中车四方所科技有限公司，重庆 400000）

0 引 言

采购供应物流配送车辆路线规划问题属于典型车辆路径问题，同时也属于非线性规划问题，在规划过程中需要考虑多种因素，包括配送路径长度、物流成本、配送时间、车辆装载能力等，综合多方面因素规划出最合理的配送线路，同时还要考虑采购供应物流配送的时效性。目前，采购供应行业不断发展，线下客户节点数量比较多、配送量比较大，因此采购供应物流配送车辆路线规划难度比较高，这也使采购供应行业面临巨大挑战。车辆路线规划关系到采购供应企业的经济效益，同时也直接关系到企业配送的服务质量，因此对配送车辆路线规划研究具有重要的现实意义和价值。由于国内关于物流配送车辆路径规划研究起步比较晚，相关理论与技术还不够成熟与完善，尤其是在当前时代背景下，用户对物流配送线路规划要求不断提高，不仅要保证规划的线路最短，同时还要保证规划线路时间成本最小，线性方法无法达到预期的规划效果，按照规划线路配送耗时比较长，传统方法已经无法满足实际需求，为此提出基于栅格遗传算法的采购供应物流配送车辆路线规划方法研究。

1 建立配送车辆线路规划目标函数

此次将采购供应物流配送车辆线路规划问题转换为线路优化问题，采用有向图建立采购供应物流配送网络，其用公式表示为

式（1）中，G表示采购供应物流配送网络；V表示所有配送节点集合，即客户节点集合，客户主要分为静态客户与动态客户；A表示连接各节点的边集；Z表示采购供应物流配送中心[1]。针对配送车辆线路规划问题提出以下假设。

假设1：每辆配送车的配送总量不能超出车辆的最大载重量；

假设2：每个客户有且仅有一辆配送车辆服务，服务次数只能每天一次；

假设3：采购供应物流配送中心能够满足所有配送点需求，不存在缺货现象；

假设4：所有车辆完成物流配送后直接返回到采购供应物流配送中心；

假设5：所有配送车辆型号相同，最大载重量相同；

假设6：在物流配送过程中不考虑交通堵塞对配送的影响。

根据以上假设，以物流配送成本最小为目标建立目标函数，其用公式表示为

式（2）中， minH表示采购供应物流配送最小成本；d1表示碳排放成本；d2表示配送车辆启动成本；d3表示油耗成本；d4表示未在规定时间内完成配送任务的惩罚成本；d5表示货损成本[2]。将其转换为另外一种形式

式（3）中，i表示物流配送中心；j表示客户节点；k表示配送车辆；sijk表示物流配送车辆由配送中心i到客户节点j的距离；cij表示物流配送中心到客户节点的距离；za表示单位配送距离成本（碳排放、车辆启动、油耗、货损等成本总和）；n表示配送车辆数量；zb表示每辆配送车辆的成本。

2 设定约束条件

在实际情况中，采购供应物流配送需要满足一定条件，根据以上建立的目标函数对配送车辆的载重进行约束，其约束条件为

式（4）中，G表示配送车辆最大载重量；uik表示客户节点由第k辆配送车辆配送的货物量；qi表示客户节点所需的货物总量；xi表示客户节点单位货位体积[3]。其次还需要满足配送时间条件，其约束条件用公式表示为

式（5）中，t表示配送车辆达到客户节点处的时刻；rijk表示一个0、1的变量，如果存在配送车辆从配送中心到客户节点的采购供应配送任务，则rijk为1，如果不存在则rijk为0；t1表示配送车辆从配送中心出发的时间；ai表示配送服务时长；t2表示配送车辆到达客户节点的时间[4]。利用以上约束条件规定配送车辆到达客户的时间点。

3 基于栅格遗传算法的最优线路规划决策

根据约束条件，利用栅格遗传算法对以上建立的目标函数进行求解，得出最优线路规划决策；该算法是将采购供应物流配送网络栅格化，将其划分为长度相同的栅格，并形成栅格地图，再用遗传算法确定采购供应物流配送车辆最优线路，其具体规划流程如图1所示。

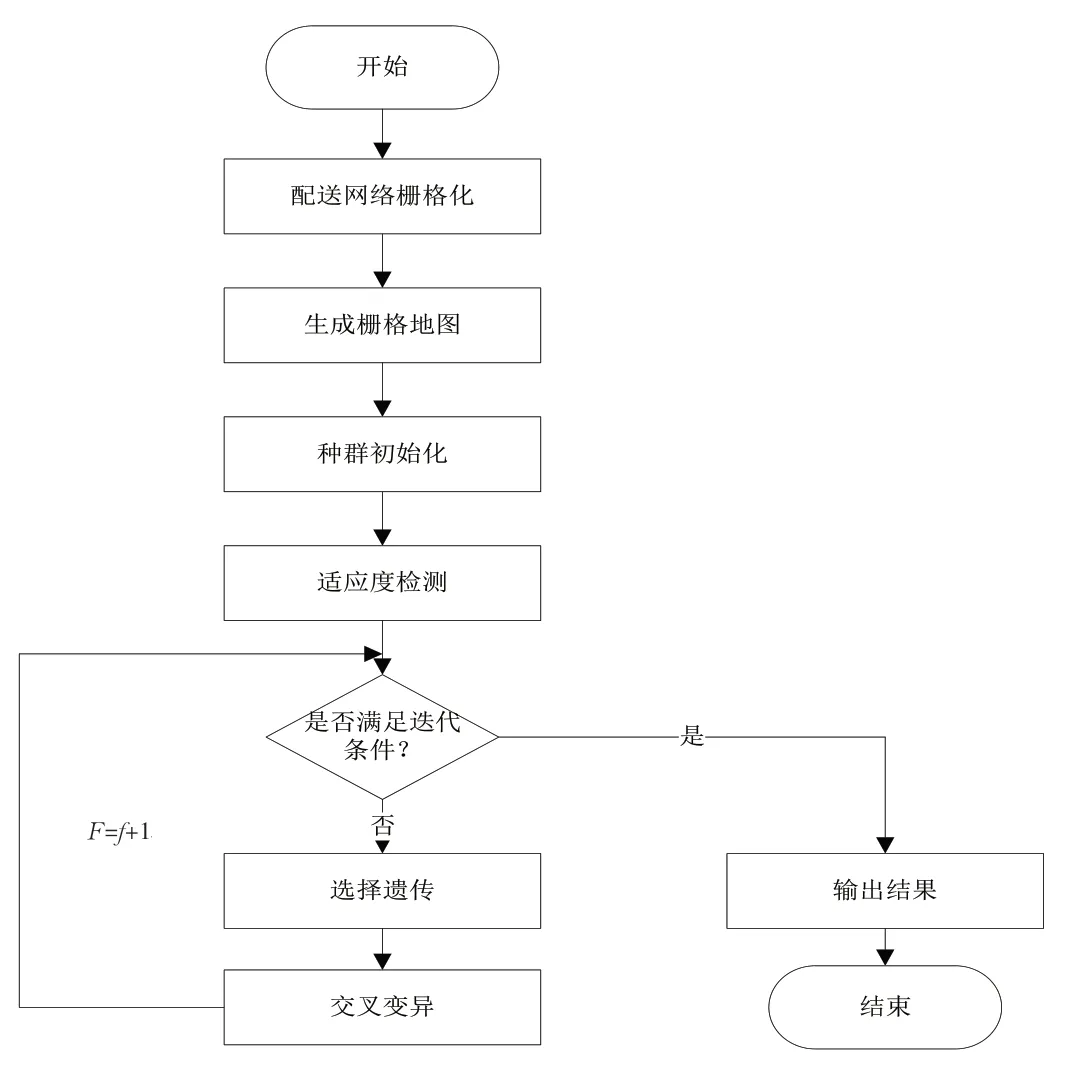
图1 基于栅格遗传算法的线路规划流程图

如图1所示，采用格雷码编码方式对配送网络进行栅格化处理，单个栅格的规格为2×2，生成栅格地图。对遗传种群进行初始化，每个遗传子代个体使用二进制进行编码，并根据实际情况设定迭代次数、遗传因子数量等参数[5]。利用适应度函数确定遗传因子个体适应度与种群适应度之间的关系，其用公式表示为

式（6）中，ε表示遗传因子个体与种群之间的适应度；k1表示遗传因子个体适应度；k2表示种群适应度；ς表示随机数；ρ表示蒙特卡洛算子。利用上述公式确定个体与种群的适应度，每迭代计算一次都检验是否满足迭代终止条件，如果满足条件则适应度最大的个体为最优线路，如果不满足则对个体进行遗传交叉与变异，交叉示意图如图2所示。

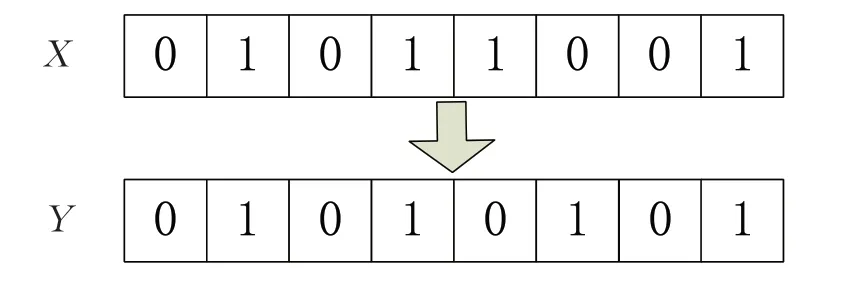
图2 个体交叉操作示意图

如图2所示，在上一代遗传因子个体中随机选择一段交叉区段，将其与子代进行基因交叉，消除相同区段，形成新遗传基因，并将其遗传给子代，再对其进行变异操作，生成新个体，迭代步数加1，再按照上述流程，直到满足迭代条件为止[6]。输出个体为最佳配送车辆线路，以此完成基于栅格遗传算法的采购供应物流配送车辆路线规划。

4 实验论证

4.1 实验准备与设计

为了验证本文设计的基于栅格遗传算法的采购供应物流配送车辆路线规划方法的可靠性与可行性，选择某采购供应企业为实验对象，该企业有7台配送车、车辆最大装货量为750kg[7]，有1个配送中心，该配送中心对应10个配送点（客户节点），分布如图3所示。

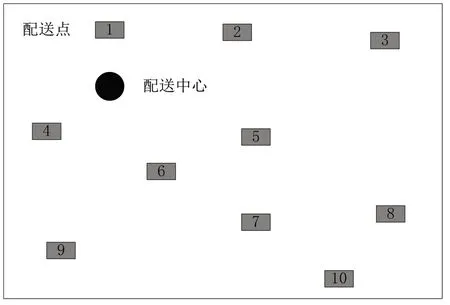
图3 采购供应物流配送平面图

利用本文的设计方法对采购供应物流配送车辆路线进行规划，并选择两种传统方法作对比，两种传统方法分别为遗传算法和改进蚁群算法，以下用传统方法1与传统方法2表示[8]。配送中出现的客户需求如表1所示。

表1 配送需求信息

按照上述流程对物流配送车辆路线进行规划，规划结果如表2所示。

表2 采购供应物流配送车辆路线规划

在可接受时间范围内完成所有货物配送，本设计方法可以完成采购供应物流配送车辆路线规划任务，以下对具体规划效果进行检验。

4.2 实验结果讨论

实验以物流配送耗时作为三种方法的性能评价指标，配送耗时最短表示规划的线路最合理，随机选取4次配送车辆路线，对4次配送耗时进行统计，根据统计数据绘制3种方法配送耗时对比图如图4所示。

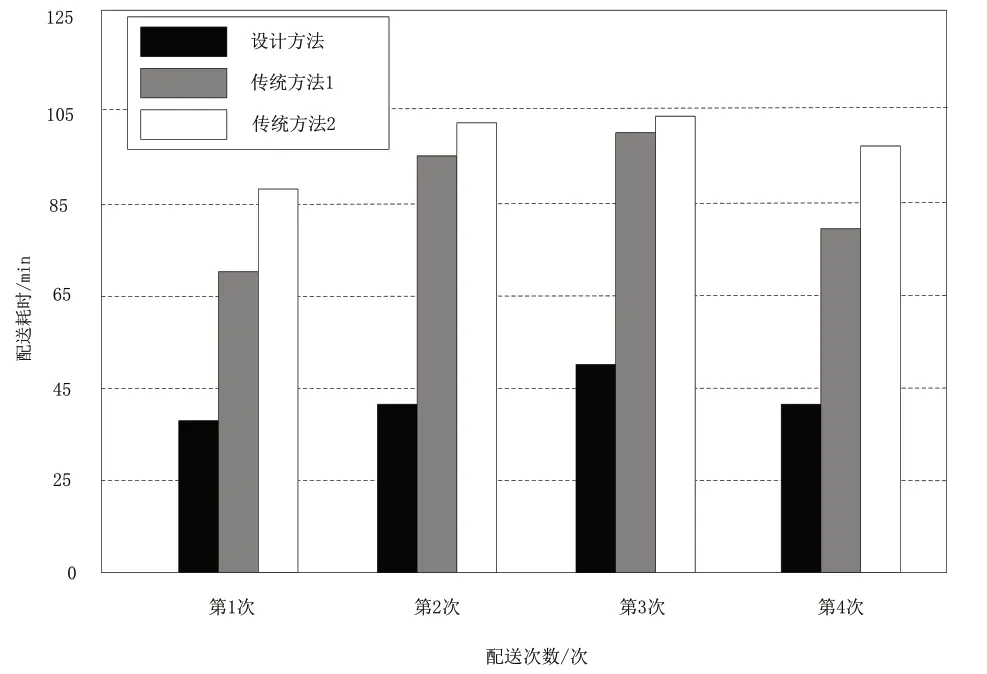
图4 3种方法规划路线耗时对比图

从图4可以看出，按照本文的设计方法规划的路线配送，配送用时比较短，与传统方法1相比，4次物流配送节约将近80分钟，与传统方法2相比，4次物流配送节约将近110分钟[9]。因此本次实验证明了本文的设计方法规划的物流配送路线的时间成本最小，规划路线的合理性优于传统方法，相比两种传统方法更适用于采购供应物流车辆路线规划。

5 结 语

本次研究针对当前物流配送车辆路线规划理论存在的不足，参考相关文献资料，将栅格遗传算法应用到线路规划中，提出了全新的规划思路，并通过实验论证了该思路的可行性与可靠性，对现有理论进行了完善，是对传统方法的优化与创新。本次研究为采购供应物流配送车辆线路规划提供了参考依据，同时对栅格遗传算法在物流配送路径规划方面的广泛应用起到一定的推广作用。