动态光散射法热/质扩散系数同时测量方法研究

高鹏，赵贯甲，尹建国，马素霞

（太原理工大学 电气与动力工程学院 循环流化床高效清洁燃烧与利用山西省重点实验室， 太原 030024）

0 引言

热、质扩散系数是流体重要的物性参数，是制冷、石油、化工等领域中的装备设计和流程优化的关键基础数据［1-3］。常规的测量方法如全息干涉法、泰勒分散法需要构建一个混合的流动过程，以获得质扩散系数，此类方法系统复杂、控制难度大，往往仅应用于常温附近实验条件，更高的温度则会叠加温度场波动影响，测量偏差较大。此外，这些方法也无法同时获取热扩散系数。斯托克斯型磁力搅拌隔膜法测量环境为室温，温度波动较大（±0.1 ℃），且仅能获得体系的质扩散系数；激光脉冲法也仅能测得流体的热扩散系数。动态光散射法是基于宏观热力学平衡后，流体体相在微观上的热力学性质涨落与宏观热力学性质间的对应关系，在一定条件下可以同时获得热、质扩散系数，而且测得的这两个参数是基于同一物理状态，是研究体相传热和传质的重要手段。

在流体热、质扩散系数测量方面，CADOGAN S P 等［4］采用泰勒分散法测量了CO2与正己烷、正庚烷、正辛烷混合体系在298～423 K 温度范围内的质扩散系数；MARBACH W 等［5］采用斯托克斯型磁搅拌隔膜法获得了正己烷与正辛烷、正十二烷、正十六烷多浓度二元混合体系在温度为298 K 时的质扩散系数；BOGATISHCHEVA N S 等［6-7］采用激光脉冲法测量了己酸甲酯、庚酸甲酯、辛酸甲酯、癸酸乙酯在305.15～400.15 K 温度范围内的热扩散系数；钟秋等［8］搭建了数字激光全息干涉法实验台，测量了碳酸乙二酯在正庚烷和空气中的质扩散系数；唐旭尧等［9］采用光散射法对R32/PAG 润滑油混合体系的黏度和质扩散系数进行了研究；崔军卫等［3］基于光散射法获得了气液二元体系的表面张力、黏度和扩散系数；李超越等［10］利用数字全息干涉法获取了CO2在RP5 航空燃油中的质扩散系数；本课题组应用所搭建的动态光散射实验系统，测量了R1243zf、R1233zd（E）［11］、R134a、正庚烷［12］和正己烷［13］的热扩散系数。利用动态光散射法同时可靠地获取流体的热、质扩散系数尚无系统的研究。

因此，利用课题组搭建的动态光散射实验平台，研究了采样时间、入射角度对实验测量的影响，确定了可以同时可靠获取二元流体热、质扩散系数的体系折射率偏差和Le数，并选取正己烷/正癸烷、正己烷/正十六烷等体系进行了验证，为基于动态光散射法流体热、质扩散系数同时测量的方法和系统开发提供了理论支撑。

1 实验材料与原理

1.1 动态光散射理论

当流体达到宏观热力学平衡，在微观上，其体相中仍存在着温度、浓度波动［14］。根据ONSAGER L［15］理论可知：局部自发性的微观波动回归到平衡状态遵循与宏观弛豫过程相同的规律，因此研究清楚微观状态下流体微元热力学参数的弛豫规律，那么与之相关的宏观热力学参数即可获得。若将一束偏振激光入射至流体体相，由于体相中温度、压力、浓度涨落导致折射率相应的涨落，激发了不同方向的散射光，这些散射光携带有体相微元涨落的信息。考虑到激光与流体为弱相互作用，流体微观波动对于激光扰动的响应可视为线性的。根据线性响应理论［16］，考察微元的涨落等价于考察由其调制的散射光的弛豫变化规律，即散射光强度的时间相关方程，这就是动态光散射法测量扩散系数的理论基础。

根据流体力学理论，流体微观温度波动的弛豫时间τC，t和浓度波动的弛豫时间τC，c与热扩散系数a和质扩散系数D12的关系分别为［17］

式中，|q|表示介电常数波动的波数的模，考虑到动量守恒，q可以由入射光波数kI（|kI| =2πn/λ0，λ0为激光波长，n为介质折射率）和散射光波数kS的差值获得

如图1，体相中入射光束照射到的区域与两个小孔PH1和PH2定义的空间立体角重合部分称为散射体积。散射体积内的电荷受到外加弱电场作用激发出散射光。动态光的散射为准弹性散射，因此可以认为散射光波数的模等于入射光波数的模，即

图1 散射体积示意Fig.1 Schematic of the scattering volume

结合式（4），当散射角θ足够小时，由图1 中几何关系可将式（3）中q的模化简为

结合图2 所示动态光散射几何示意图，根据折射定律n0sinΘi=n1sinφ=n2sinθ，式（5）可简化为

图2 动态光散射几何示意Fig.2 Schematic of dynamic light scattering geometry

式中，n0、n1、n2分别为激光在空气、窗口、介质中的折射率。

在外差条件下，散射光强度IS（=IS，t+IS，c，IS，t为温度波动引起的散射光强，IS，c为浓度波动引起的散射光强）远小于参考光强度ILo，二元混合体系局部温度、浓度波动引起的散射光强度的时间相关函数可以表示为［18］

式中，b0为基线项，表征了散射信号的本底噪声，主要受颗粒运动和外界振动等因素的影响，取值接近于1；b1（≈2IS，t/ILo）和b2（≈2IS，c/ILo）分别为温度扩散项和浓度扩散项信号的对比度，在外差模式下均在2%以内，此时可确保ILo>100IS，t或IS，c。结合式（1）和（2），可获得热、质扩散系数。

1.2 实验材料

实验试剂详细信息如表1。实验前，采用孔径为2 μm 的聚四氟乙烯过滤器除去液相中纳米级颗粒。

表1 化学试剂基本信息Table 1 Detailed information of chemical sample

1.3 样品制备

为研究体系折射率偏差等因素对～实验结果的影响，选取三组体系，详细参数如表2。表中x1表示二元混合体系组分1 的摩尔分数，n3、n4分别为组分1、2 的折射率。

表2 i～iii 组二元体系参数（T = 298 K）Table 2 i～iii groups of binary system parameters at 298 K

在实验样品制备中，使用精度为0.000 1 g 的电子天平（Mettler Toledo，型号： LE204E）称量各组分的质量，不确定度为±0.000 2g。为保证混合体系均一稳定，实验前使用磁力搅拌器以200 r/min 转速匀速搅拌1 h。氮气（vol.=99.99%）作为保护气充入样品池，避免实验过程中试剂高温氧化。

2 实验系统与结果分析

2.1 散射光路

实验系统如图3，单纵模激光器功率为1 W，激光波长为532 nm，实验时激光器采用功率为700 mW，经过长焦透镜准直以减小激光光束发散，准直后的激光采用二分之一零级玻片和偏振分光棱镜的组合调整激光的光强和偏振状态，再经反射镜反射至分光平片，分为两束光路。其中反射光束作为探测光，以300 mW功率入射至液体体相，由于液体透明且光强较弱，不会产生热透镜作用，因此加热效应可以忽略。该反射镜安装在高精度转台上，角度分辨率为0.000 67°，用来精确控制激光入射角度；透射光束作为参考光，经中性密度片衰减后，通过反射镜入射液体体相，与散射光发生混频。混频后的光束穿过小孔被探测器接收，经光纤分束器分光产生具有一定时间延迟的两束光，这样的设计避免了当采样时间很短时，单光子计数器产生的后脉冲效应对实验测量的干扰。两束光分别在光子计数器将光信号转为电信号，电信号经过数字相关器用式（7）进行拟合，最终获取被测液体体相的弛豫时间τC，t和τC，c。

图3 动态光散射实验系统示意与实物Fig.3 Schematic and physical map of the dynamic light scattering experimental system

2.2 实验本体与控温系统

图4（a）为高温高压样品池示意图，由316 不锈钢制作而成。四个石英窗口用O 形圈密封，其中前后窗口用于激光透射，左右窗口为观察窗口；样品池顶部预留样品注入口；另外，两个盲孔用以安装控温及测温高精度铂电阻温度计。图4（b）为实验系统温度控制系统示意图，样品池外侧均匀缠绕电加热丝，为了保持温度稳定，电热丝外层包覆5 mm 厚的保温层，并在样品池外侧整体加装隔热箱体。温度控制分别由温控器（Fluke，2100）和测温仪（ASL，F200）精确控制，测温精度为±10 mK，系统温度波动为±5 mK，温度测量的扩展不确定度为30 mK（k=2）。

图4 实验本体与温度控制系统示意图Fig.4 Temperature regulation schematic of the experimental system

2.3 不确定度分析

热扩散系数和质扩散系数的不确定度［21］计算式分别为

其中波数的不确定度来自激光的波长、入射角和折射率，激光波长的不确定度为Δλ/λ=0.02/532=0.003 8%，入射角Θi的不确定度ΔΘi/Θi为0.000 67/1=0.067%，折射率的不确定度为Δn/n=0.004/1=0.4%，因此波数的不确定度Δq/q=0.41%（k=2）。对于混合流体，温度、浓度波动的弛豫时间的标准不确定度分别为2%和3%，因此热扩散系数和质扩散系数的不确定度分别为4.32%和6.22%（k=2）。

2.4 入射角度与采样时间的选择

由于入射角度和采样时间对实验影响较大，因此确定合理的采样时间和入射角度十分重要。一般地，二元混合体系中温度波动弛豫较快，而浓度波动弛豫较慢，因此，若采样时间过短，浓度波动的信号将无法全面包含；而采样时间过长，外界低频机械振动噪声将严重影响信号。因此选择合适的采样时间是可靠测量的重要因素之一。

入射角度过大，会使散射光强和弛豫时间急剧减小，很难保证探测信号的信噪比，同时温度信息的表达也会较为粗略，导致热扩散系数测量偏差增大；反之，入射角度过小，质扩散变慢，所需采样时间增加，则测量值同样会受低频噪声的影响。根据实验验证，采样时长为浓度波动弛豫时间的1.5～3 倍且激光入射角为8°～12°时，实验系统具有较高的测量可靠性。

图5 为等摩尔分数的正己烷/正癸烷体系在T=298 K， 采样时间为250 μs，Θi=8.0°时获得的自相关函数。该自相关函数分别包含了局部温度波动和浓度波动两个模式，这两个模式分别用虚线和点划线表示，通过式（7）拟合后得到的温度、浓度波动的弛豫时间分别为τC，t=（4.42±0.055 1）μs和τC，c=（148.28±5.020 2）μs，不确定度分别为1.24%和3.38%。实验值与拟合方程最大偏差为0.036%，说明式（7）能够较好地拟合实验数据，拟合结果如表3。

表3 时间自相关函数参数拟合结果Table 3 Fitting results of time autocorrelation function parameters

图5 等摩尔分数的正己烷/正癸烷体系归一化强度相关函数及偏差Fig.5 Normalized intensity correlation function and deviation of equimolar fraction of n-Hexane/n-Decane system

2.5 结果分析

2.5.1 流体动力学模式验证

表4 为T=298.15 K，饱和状态下采用入射角范围为8°～12°时测得的第i 组体系弛豫时间，并取倒数。若当波数模长q→0 时，τC，t（q）→∞和τC，c（q）→∞，即体系温度和浓度波动引起的波的生命周期将无限长，符合这样特征的波动模式即为流体动力学模式［22］。考察τ−1C，t和τ−1C，c分别与q2的关系，如图6（a），弛豫时间的倒数与q2为过坐标零点的直线，很好地满足上述定义，因此流体体相由温度和浓度局部波动激发的波是流体动力学模式。

表4 流体动力学模式验证数据Table 4 Validation of hydrodynamic modes

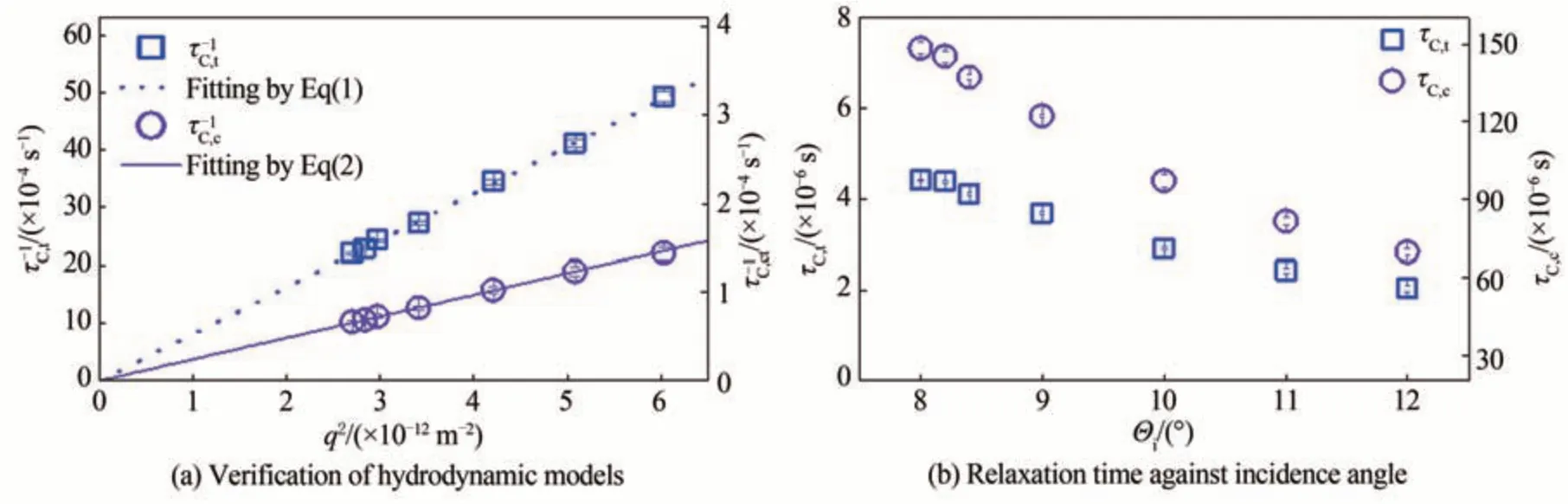
图6 等摩尔分数的正己烷/正癸烷体系温度波动和浓度波动的流体动力学验证模式及入射角-豫时间关系Fig.6 Hydrodynamic modes verification for temperature and concentration fluctuations of n-Hexane/n-Decane system with equal molar fraction and relation between incident angle and relaxation time

三组体系分别在298.15～393.15 K、298.15～448.15 K 和298.15～398.15 K，饱和状态下测得热、质扩散系数实验数据，同时将来源于NIST REFPROP 10.0［23］热扩散系数数据和文献中质扩散系数［5，24］列于表5。表中a*为NIST REFPROP 10.0 热扩散系数数据［23］，、为质扩散系数文献数据［5，24］。

表5 i～iii 组体系热、质扩散系数实验数据及文献和NIST REFPROP 10.0 数据Table 5 i～iii Thermal and mutual diffusivity experimental data and literature data and NIST Refprop 10.0 data

将测得的热、质扩散系数实验数据分别拟合为关于温度的三次多项式，即

式中，a0～a3，D0～D3分别为热、质扩散系数关联式的拟合参数，详细结果如表6。

采用最大偏差（Maximum Relative Deviation，MRD）和平均绝对偏差（Absolute Average Relative Deviation，AARD）评估关联式拟合结果，其定义分别为

式中，Expi、Calci分别表示热/质扩散系数实验数据和拟合关联式（10）、（11）的计算值，N表示实验数据点数。

图7 为i 组体系在298.15～393.15 K，饱和状态下热、质扩散系数实验数据，同时将NIST REFPROP 10.0 和文献数据示于相同图中。其中，热扩散系数实验数据采用式（10）拟合，实验值与关联式计算值之间最大偏差为1.50%，平均绝对偏差为0.66%。本系统所测热扩散系数与NIST REFPROP 10.0 所得数据趋势相同，且平均偏差在4.00%以内；质扩散系数采用式（11）拟合的最大偏差为2.00%，平均绝对偏差为1.06%。与文献值比较，偏差为3.56%且在不确定度范围内可以互相覆盖，很好地验证了本文实验系统同时测量热、质扩散系数的可靠性。

图7 等摩尔分数的正己烷/正癸烷体系热扩散系数实验数据与拟合方程及NIST REFPROP 10.0 数据对比Fig.7 Comparison of experimental data and fitting equation of thermal diffusivity of n-Hexane/n-Decane system with equimolar fraction and NIST REFPROP 10.0 data.

2.5.2 实验结果分析

图8、9 分别给出了ⅱ，ⅲ组体系分别在298.15～448.15 K 和298.15～398.15 K 饱和状态下热、质扩散系数的实验值以及文献数据。热扩散系数与拟合方程计算值最大拟合偏差分别为1.10%和1.00%，平均绝对偏差分别为0.34%和1.95%；质扩散系数最大偏差分别为5.62%和1.00%，平均绝对偏差分别为2.58%和0.31%。ii 组体系质扩散系数与MARBACH W［5］等所测数据偏差为0.86%，且在误差棒范围之内。

图8 摩尔分数为0.06/0.94 的正己烷/正十六烷体系热、质扩散系数实验数据与拟合方程及文献值比较Fig.8 Comparison of the experimental data of thermal diffusivity and mutual diffusivity of n-Hexane/n-Hexadecane system with mole fractions of 0.06/0.94 respectively， fitted equations and literature values

图9 摩尔分数为0.852/0.148 的正己烷/正十六烷体系热、质扩散系数实验数据与拟合方程Fig.9 Experimental data and fitting equation of thermal diffusivity and mutual diffusivity of n-Hexane/n-Hexadecane system with mole fractions of 0.852/0.148 respectively

从图7～9 可以直观地看出，三组体系热扩散系数随温度升高而减小，不确定度随温度变化较小，质扩散系数随温度升高而增大，不确定度随温度变化较大。热扩散系数平均不确定度分别为3.46%、2.61%和2.49%；质扩散系数平均不确定度分别为3.58%、5.16%和2.25%。

Le 值过大或过小时，扩散系数实验值不确定度均较大，因此Le 值可作为动态光散射法同时测量热、质扩散系数可靠性的判断依据。此外，实验发现Le 数随温度的升高而减小，扩散系数的不确定度随Le 数的减小，先减小后增加，趋势与PISZKO M 等［25］测得的一致。当Le 接近100 时，热扩散系数的不确定度较小，为3.81%，质扩散系数的不确定度较大，达到了9.89%；当Le 数接近10 时，热、质扩散系数的不确定度均逐渐增大，且热扩散系数的不确定度变化幅度小于质扩散系数的不确定度；当Le 数接近1 时，温度、浓度波动的信号较难分开，同时测量会导致不确定度偏大。综上Le 数在10～80 的范围内，同时测得热、质扩散系数不确定度在5%以内。

由ii，iii 组体系的数据对比可知在相同温度下，折射率偏差较大的组热、质扩散系数测量结果的不确定度较小，与KOLLER T M 等［26］的结果吻合，由此分析，当折射率偏差较小时，通常温度波动的信号占据主导，导致温度、浓度波动信号较难分开。选取折射率偏差大于4%的体系精度较高，不确定度在4%以内。

由ii，iii 组体系的数据对比可知黏度对于热扩散系数的测量精度影响较小，质扩散系数测量精度受黏度影响较大。由此分析二元体系黏度的增加，混合物组分的流动性降低，减缓了微观浓度波动的衰减，使得采集的信号受到削弱，在低温环境下尤为显著，随着温度的增加，体系的黏度有所下降，微观浓度波动增加强，不确定度逐渐减小。

3 结论

本文系统地研究了采用动态光散射法同时获得二元液相混合体系热、质扩散系数的方法。通过测量正己烷/正癸烷与正癸烷/正十六烷等二元混合体系的扩散系数，得到以下结论：1）本系统测量等摩尔分数的正己烷/正癸烷体系的热、质扩散系数与拟合值最大偏差分别为1.5%和2%，平均绝对偏差分别为0.66%，1.06%，与文献值比较，偏差为3.56%，验证了该系统同时测量热、质扩散系数的可靠性。2）获得了正己烷/正癸烷、正己烷/正十六烷和正己烷/正十六烷摩尔分数分别为0.50/0.50、0.06/0.94、0.85/0.15 在饱和状态下温度范围分别为298.15～393.15 K、298.15～448.15 K 和298.15～398.15 K，的热、质扩散系数及其关联式。3）推荐采样时间为浓度波动弛豫时间的1.5～3 倍，激光入射角为8°～12°，测量的准确性较好，与文献值偏差在4%以内。4）当待测体系满足折射率偏差大于4%或书Le 数在10～80 区间时，同时测得热、质扩散系数的不确定度在5%以内。