基于数值方法的AUV 近水面运动特性研究

王旭辉，林扬，王定前，孟令帅，高浩，曹新星，谷海涛

(1.东北大学 机械工程与自动化学院，辽宁 沈阳 110819；2.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；3.中国科学院机器人与智能制造创新研究院，辽宁 沈阳 110169；4.中国人民解放军32033 部队，海南 海口 570000)

0 引言

自主式水下航行器（autonomous underwater vehicle，AUV）可自身携带能源，并配备多种传感器，依靠自制能力在水下完成被赋予的各种任务[1]。AUV 自主性高，机动性好，在军事和民用领域得到了广泛应用。但受到目前能源技术水平的限制，AUV 不能长时间在水下作业，为及时补充能源和传输数据，需对其进行回收。目前AUV 回收方式可分为有人回收和无人回收2 种，有人回收方式主要依靠操作人员在母船上通过起吊装置将AUV 起吊至甲板，而无人回收又可细分为水面回收和水下回收2 种方式[2]。无论是有人回收还是无人水面回收，回收过程的最终阶段都需要AUV 在近水面航行，以便将AUV 回收至母船甲板上。为了提高回收成功率，需对AUV 近水面动力学特性进行研究。学者们对各种不同类型AUV 的动力学特性进行了大量研究工作，但大部分的研究是以深水场景为前提的[3– 6]。在近水面情况下，AUV 的运动受到自由液面的影响，会有与深水状态不同的运动特性[7– 10]。

本文以AUV 的无人水面回收为背景，分析不同潜深情况下自由液面对AUV 运动的影响同时，结合水面回收场景，分析特定潜深下的AUV 水动力特性，并求解水动力系数，建立AUV 的近水面运动模型。最后，通过运动轨迹仿真对所建立的AUV 运动模型进行验证。

1 模型

1.1 AUV 参数

研究对象为50 千克级AUV，按照美军2000～2004 年间发布的《美海军UUV 总体规划》中给定的潜航器分级标准，将该小型AUV 称为便携式AUV[11]。便携式AUV 的原始模型如图1 所示。

图1 便携式AUV Fig.1 Portable AUV

便携式AUV 主体上有天线、舵板以及推进器导流罩等，主体以外的装置称为附体。相对于AUV 主体来说，附体在CFD 计算中，附体会极大增加划分网格的工作量，增加计算时间，降低计算精度，同时使计算结果难以收敛。为了解决上述问题，将AUV 原始模型进行适当简化，在CFD 计算模型中，去除对计算结果影响较小但对计算难度影响较大的附体。简化的AUV 模型如图2 所示，习惯上称之为光体。其体长为2 593 mm，直径为250 mm。

图2 简化模型Fig.2 Simplified model of AUV

1.2 数值计算方法

粘性流动数值求解的本质是求解纳维-斯托科斯（Navier–Stokes，N–S）方程[12]。根据雷诺数计算公式可以看出，AUV 近水面运动过程是一个湍流过程,目前湍流的数值模拟方法主要有直接数值模拟（direct numerical simulation,DNS）、大涡模拟（large eddy simulation,LES）、雷诺平均方程（reynolds-averaged navier-stokes equations，RANS）等。DNS 方法没有对湍流流动做任何简化，直接求解N–S 方程，理论上可以得到精确的计算结果。但在实际应用中，DNS 方法耗费巨大，目前仅能应用在低雷诺数的简单湍流中；LES 方法对N–S 方程做了一定简化，该方法认为，大尺度涡对流动的影响较大。通过N–S 方程直接求解，而小尺度涡对流动的影响较小，可通过模型对其进行刻画。LES 方法在计算量上小于DNS 方法，但对于实际应用来说，该方法的计算量仍然偏大，需要高性能的计算设备才能实现；RANS 方法顾名思义，是对N–S 方程进行平均化处理，忽略了流动的细节，放弃模拟非定常流动，计算平均意义下的流动结果。N–S 中的非线性项平均化后会产生雷诺应力项，需引入湍流模型对其进行处理。RANS 方法计算量小，在工程实践上得到了广泛应用。考虑到时间成本与现有计算资源，选用RANS 方法进行便携式AUV 的近水面运动模拟。

RANS 方程可写为：

式中，τR为雷诺应力。

要求解RANS 方程，必须引入湍流模型，应用k−ε两方程模型。湍流动能k和湍流耗散率 ε的传输方程可写成如下形式：

1.3 AUV 运动方程

建立图3 所示的惯性坐标系和随体坐标系，并定义相关符号。E−ξηζ为惯性坐标系，固定于地球，不随AUV 运动，可简称为定系；G−xyz为随体坐标系，随AUV 一同运动，可简称为动系，x，y，z为动系相对于定系的坐标值；φ，θ，ψ分别为动系相对于定系的姿态角（横倾角、纵倾角、首向角）；V为AUV 在定系下的速度；Ω为AUV 在定系下的角速度；F为作用在AUV 上的力；M为作用在AUV 上的力矩。V，Ω，F，M又可表示为动系G−xyz上的分量，如表1 所示。

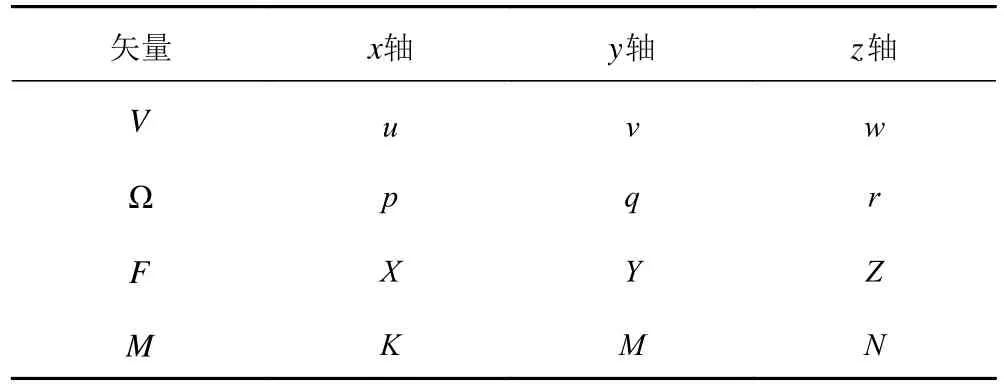
表1 矢量的各轴分量Tab.1 The components of each axis of the vector

图3 坐标系示意图Fig.3 Schematic of the coordinate system

在AUV 近水面运动过程中，假设动系G−xyz原点与重心位置重合，整个运动过程中AUV 整体浸没于水下，重、浮心位置不变。忽略整个运动过程中AUV 的横滚，根据潜艇标准运动方程[13]，便携式AUV 六自由度运动方程无因次形式如下式：

1.4 仿真环境

采用CFD 软件进行仿真计算，利用Q=h/D表示AUV 的下潜深度，h为AUV 轴线距自由液面距离，D为AUV 直径如图4 所示。L为AUV 轴向长度，计算域几何尺寸如图5 所示。计算域外形为立方体，长6L，宽2.4L，高3.5L，AUV 尾部指向面为压力出口，其余5 个面设置为速度入口。

图4 仿真场景示意Fig.4 Illustration of the simulation scene

图5 计算域示意Fig.5 Illustration of the computed domain

1.5 网格无关性与精度

CFD 方法求解水动力问题需要消耗大量计算资源。本文采用的求解方法是RANS方法，对于RANS 方法，由于湍流模型的引入，当网格达到一定密度之后，继续增加网格密度对计算结果影响不大。同时，由于离散误差的存在，网格密度过大时误差反而可能增大。为了合理利用计算资源，首先进行网格无关性验证，即在误差合理的情况下，用最粗糙的网格进行计算。为了保证更改网格密度后网格质量不变，最优方法是成倍数加密网格，但是对于三维问题来说，每次网格量需要至少增加8 倍，这种方法在实际操作中不可行。本文验证网格无关性的方法如下：首先按照经验大致划分一套初始网格；再根据网格情况通过调整基础尺寸的方式调整网格密度，将不同网格密度下的计算结果进行比较；选取最合理的一套网格为最终的计算网格。

针对潜深Q=1 的直航工况，通过调整基础尺寸的方式生成5 套不同密度的计算网格。同时，通过对比不同网格密度下的相对误差e来验证网格无关性。e的定义如下式：

式中：ex为轴向力相对误差；ez为垂向力相对误差；X为轴向力；Z为垂向力；i为网格序号。

网格参数与计算结果如表2 所示。根据计算结果，同时考虑到实验室计算资源配备情况，最终选取第4 套网格作为后续计算标准。

表2 网格无关性工况设置Tab.2 Grid-independent scenario settings

为了确定网格划分方法的计算精度，采用REMUS 100 AUV 进行验证。REMUS 100 AUV 外形尺寸与本文研究的AUV 相近，其在试验中测得的阻力系数为cd=0.118347[14]。在上述网格参数设置的情况下进行REMUS 100 AUV 的阻力系数数值计算，得到结果为cd=0.124262，与试验数据误差为4.998%，满足工程要求。

2 数值计算过程

x，y，z分别为AUV 随体坐标系在惯性坐标系下的坐标；u，v，w分别为AUV 速度V在随体坐标系3 个坐标轴上的投影；p，q，r分别为AUV 角速度 Ω在随体坐标系3 个轴上的投影；φ，θ，ψ分别为横倾角、纵倾角和首向角。

2.1 自由液面对运动的影响

为了分析自由液面对AUV 运动的影响，分别设置潜深Q=1，1.5，2，2.5，3，3.5，4，航速0.5 kn，1 kn，1.5 kn，通过分析阻力变化探究自由液面对AUV 运动的影响。给定来流速度为1.0288 m/s，不同情况下的阻力变化如图6 所示。

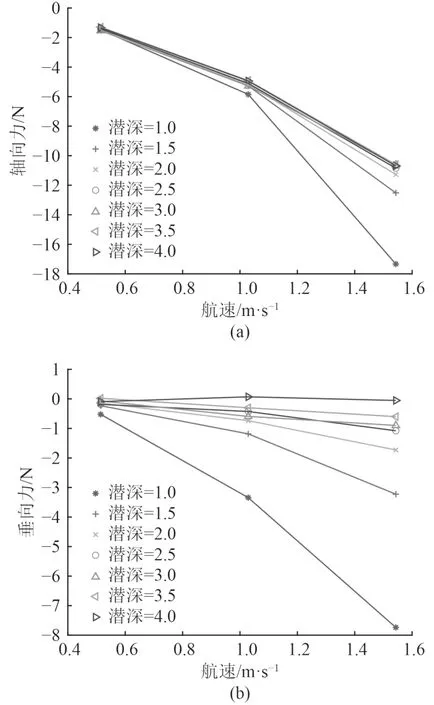
图6 轴向力与垂向力变化情况Fig.6 Changes in axial and vertical forces

可以看出，自由液面会增大AUV 航行过程中的阻力，同时产生垂直向上的吸力。随着潜深逐渐增加，自由液面所带来的影响逐渐减小，在潜深达到4 倍直径时，影响可忽略不计。

2.2 直航运动

2.3 PMM 运动

PMM 属于拘束船模试验的一种，通过强制AUV作规定运动，获取AUV 受到的力与力矩，从而求得AUV的水动力系数。通过数值模拟横荡、首摇、纵荡、纵摇4 种运动，求解相应的水动力系数，运动规律如下式：

式中：a为运动振幅；ω为运动频率。

通过PMM 模拟方式得到的水动力系数会受到运动频率的影响，在不同频率下得到不同的数值，因此依靠单个工况获得水动力系数是不合适的。目前常用的处理方法是，求解不同频率下的水动力系数，之后通过过原点拟合或平均化处理的方式进行近似处理，得到较为合理的最终结果[15]。

为减小仿真工况对系数的影响，拟合不同周期下的系数，通过平均化处理的方式求得平均值。同时，通过拟合优度R2衡量拟合得到的水动力系数的适用性。R2定义式如下式：

式中，i为不同的仿真组数标号。可以看出，R2越接近1，表示水动力系数系数对原始数据的适用性越好。

3 结果与验证

3.1 水动力系数

在潜深Q=1.5 工况下，不同周期下对应的水动力系数如表3 所示。

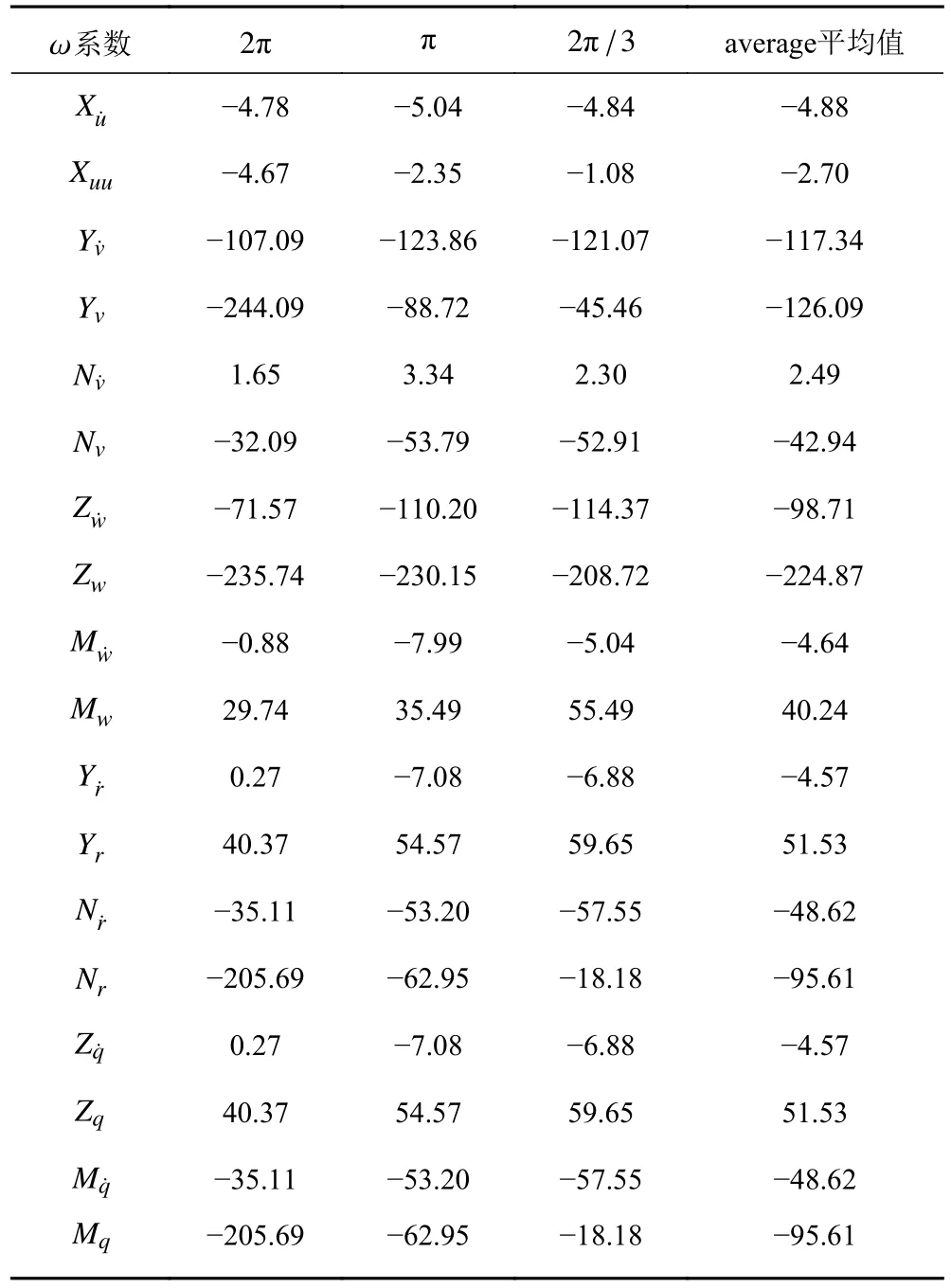
表3 水动力系数表Tab.3 Summary table of hydrodynamic coefficients

拟合精度如图7 所示。

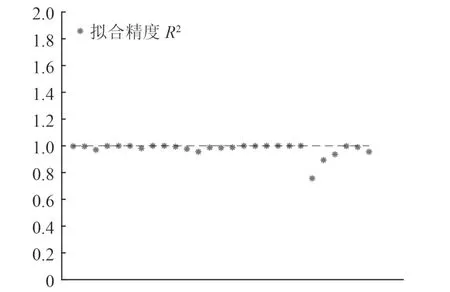
图7 拟合精度汇总图Fig.7 Fit the accuracy summary graph

可以看出，拟合精度R2绝大部分都在1 附近，证明水动力系数拟合精度良好。

3.2 轨迹仿真验证

通过CFD 模拟直航运动轨迹与运动方程模拟直航运动轨迹的对比，验证运动方程的准确性。CFD 直航运动模拟场景如图8 所示，潜深Q=1.5，添加一阶波浪。基于运动方程的直航运动模拟通过Simulink 实现，波浪力以操纵力的形式出入到运动方程中,仿真模型如图9 所示[16，17]。

图8 CFD 直航模拟场景Fig.8 CFD direct flight simulation scenario

图9 运动方程模拟仿真模型Fig.9 Simulation model of the equation of motion simulation

基于运动方程的直航轨迹模拟与基于CFD 的直航轨迹模拟在3 个方向上的位移分量结果如图10 所示。

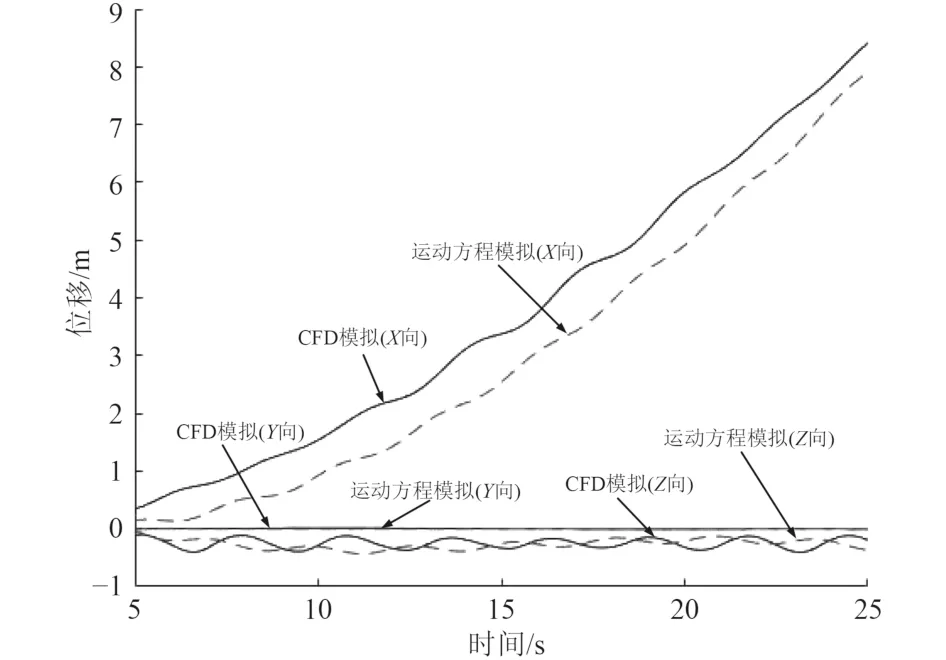
图10 直航轨迹仿真结果图Fig.10 Trajectory simulation result graph

数据误差统计情况如表4 所示。

表4 数据误差统计表Tab.4 Statistical table of data errors

可以看出，X向与Z向数据误差较小，Y向误差较大，其原因是Y向位移基准值很小，导致计算出的误差偏大。

4 结语

本文以水面自主回收AUV 为背景，对便携式AUV 的近水面运动特性进行研究。在分析自由液面对AUV 运动影响的基础上，针对其潜深Q=1.5 时的近水面水动力系数进行求解，并建立运动方程。最后，通过仿真运动轨迹方式对所得到的运动方程进行验证。

结果表明，受到自由液面的影响，AUV 航行过程中会受到X轴负向的阻力和Z轴正向的升力，且影响程度随着深度的增加逐渐减小。在深度超过4 倍AUV 直径后，影响可以忽略不计。CFD 方法模拟直航轨迹与运动方程模拟直航轨迹得到的结果误差较小，证明水动力系数及运动方程的准确性。