湖南地区应力场定量结果及置信区间分析

田优平　沈平　万永革　唐红亮　康承旭　姚海东　佘旭明

摘要：基于湖南及其邻区312个地震的529条P波初动极性数据和32个M_L≥2.8地震的震源机制解，采用格点尝试法和网格搜索法分别反演得到了湖南地区构造应力场的定量结果和置信范围。格点尝试法计算得到的P轴方位和倾伏角分别为102°和10°，T轴方位和倾伏角分别为237°和76°；网格搜索法反演得到的P轴方位和倾伏角分别为100°（置信区间为79°～100°）和5°（置信区间为2°～5°），T轴方位和倾伏角分别为225°（置信区间为204°～225°）和81°（置信区间为81°～82°）。结果表明：湖南地区平均震源机制解表现为逆断型；主压应力轴优势方位为NWW向，倾伏角近乎水平；主张应力轴优势方位为NE—NEE向，倾伏角较大。对两种方法得到的研究区应力场结果进行了可靠性分析并与前人结果进行了对比，证实本文结果的可信度较高。

关键词：应力场；格点尝试法；网格搜索法；置信区间；湖南地区

中图分类号：P315.727文献标识码：A文章编号：1000-0666（2023）04-0483-08

doi：10.20015/j.cnki.ISSN1000-0666.2023.0052

0引言

构造应力场研究是地学研究的重要分支，不仅有助于我们认识地震孕育、发生及其与深浅部构造背景之间的关系，在研究煤油气等矿产分布、地壳构造演化和地震危险性分析等方面也发挥着重要作用。邓起东等（1979）根據地震、地质构造和地壳形变等资料，探究了我国构造应力场自晚第三纪以来的基本特征，讨论了应力场与板块运动间的关联；鄢家全等（1979）通过浅源地震的断层面解结果等资料讨论了我国及邻区构造应力场区域特征；许忠淮等（1983）在Aki（1966）综合震源机制解方法的基础上提出了格点尝试法，基于P波初动资料推测了华北地区构造应力场的方向，并分析了运用多个小震数据的优势，汪素云和许忠淮（1985）应用该方法计算了我国东部大陆应力场的方向；谢富仁等（2003）论述了全球构造应力场分布的主要特征；徐纪人等（2008）以大量中强地震的震源机制解为基础研究了我国大陆地壳应力场与构造运动；万永革等（2011）提出了综合震源机制解方法，基于P波初动极性数据反演了中国台湾地区三维应力场结果，随后，此方法被广泛推广应用（盛书中等，2015；田优平等，2020）；万永革（2012）首次提出了基于震源机制的网格搜索法求解构造应力场，结果表明该方法在一定程度上提高了应力场的反演精度；田优平等（2014）通过GPS资料讨论了三河—平谷地震区的应力特征；吴啸龙等（2020）利用震源机制解和GPS实测速度场反演得到了喜马拉雅构造带应力场结果。

以往对我国华南地块（张培震等，2003）构造应力场的研究（邓起东等，1979；鄢家全等，1979；丁旭初，张文涛，1988；徐纪人等，2008；陈益明，1992；谢富仁等，2003；郭良迁等，2012）表明，华南地块主压应力轴方位以NWW和NW向挤压为主。湖南地区位于华南地块，上述研究中有些虽包含了湖南地区构造应力场结果，但大多是从较大尺度上来勾画其特征。也有少数学者定量给出了湖南地区应力场的方向：蒋维强等（1992）基于小震震源机制资料，对华南地区地壳应力场进行计算，结果显示湖南地区主压应力场方向为NNW向（方位角为334°），主张应力场方向为NEE向（方位角为242°）；汪素云和许忠淮（1985）研究表明，湖南地区P轴方位角为80°，倾角3°，T轴方位角为353°，倾角29°。由于湖南地区地震活动性较弱，因此，学者对该地区的关注度并不高，专门针对湖南地区应力场的研究较少，且由于资料有限，现有湖南构造应力场结果可靠性并不高。近年来，随着数字化地震台网的不断加密，地震监测能力随之增强，小震资料愈加丰富，使其在构造应力场研究中有着较好的应用前景，如田优平等（2020）利用综合震源机制解方法反演得到了湖南地区0.2°×0.2°二维构造应力场结果，定性讨论了区域应力场总体分布特点，并对湘东、湘西、湘南、湘北、湘中各区应力场特征进行了分析，该方法的优点是既不需要直接求解震源机制解，又能充分利用区域大量的小震数据来计算应力场，但该研究未给出湖南地区总体应力场的定量结果及置信区间。

为了进一步分析湖南地区应力场并给出定量结果和置信范围，本文拾取2009—2019年湖南及其邻区312个地震的529条清晰的P波初动数据，首先采用格点尝试法定量计算湖南地区平均应力场结果，然后计算32个ML≥2.8地震的震源机制解，利用网格搜索法反演得到湖南地区构造应力场及置信区间，最后对比不同方法得到的应力场结果并分析可靠性，探讨应力场与区域构造之间的关系，以揭示该区构造应力背景，为区域地震孕育、发生及未来地震趋势判定提供基础。

1资料来源

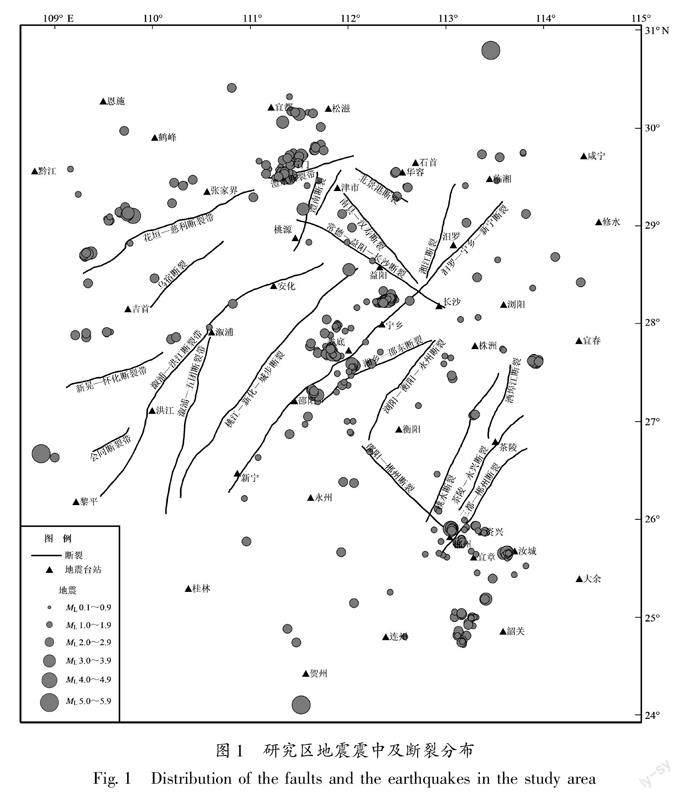
笔者从湖南地震台网编目震相报告中获取了2009—2019年湖南及其邻区（108°～115°E，24°～31°N）42个地震台站记录到的632个地震的记录资料（图1）。本文使用的地震资料时间跨度在10年以上，这样既可以充分利用该区域的地震资料，又能改善地震的覆盖范围，从而使计算结果相对稳定可靠。为了保证初至P波方向的准确性，舍弃记录不清晰的数据并重新读取地震波形资料（田优平，2015；田优平，赵爱华，2016），最终拾取了312个地震的529条清晰的P波初动极性数据。研究区地震震中及活动断层分布如图1所示。

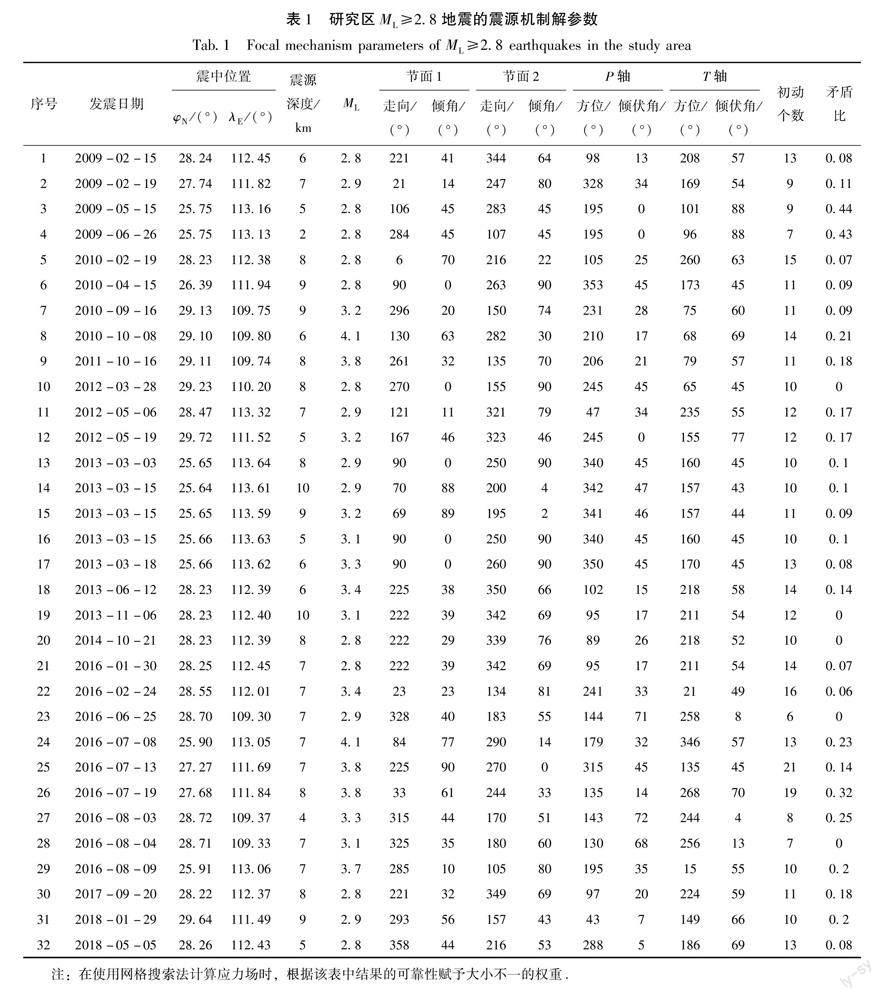
笔者使用基于P波初动数据求解单个地震震源机制解的方法计算了研究区M_L≥2.8地震的震源机制。为了保证震源机制结果的可靠性，本文尽量选取初动个数大于8个、初动较清晰且初动符号在震源球面上分布较为均匀、对震中包围较好的地震（关鹏虎等，2022），计算得到了32个地震的震源机制解结果（表1）。

2研究方法

2.1格点尝试法

当P波初动方向资料数量不足或混有错误符号，导致在震源球面上难以获得足以限制两个节面位置的数据覆盖时，采用其它解析计算方法求节面解往往依赖于初值选择，稳定性并不高。鉴于此，许忠淮等（1983）提出了基于P波初动的格点尝试法，该方法主要根据多个地震在多个源、近台站上的P波初动方向记录，确定与平均节面解对应的P、B、T轴，其主要思路是：按照震源双力偶点源模型，震源机制解可由震源处“震源坐标系”在地平坐标系中的3个独立变化的角度A_z、i_h、R确定，其中，A_z、i_h分别为台站方位角和射线离源角。使用格点尝试法按照10°×10°×10°的步长对这3个角度所有可能的取值逐一进行尝试，找出一组A_z、i_h、R对应的2个理论正交节面，可将观测的P波初动方向分为正负相间的四象限，使得与此象限划分矛盾的观测数据最少，即矛盾比最低，然后根据观测数据拟合最佳的一组A_z、i_h、R，即可得到最佳震源机制解。为避免最佳解的不确定性，根据矛盾符号比在最低值和“最低值+5％”之间所有可能的P、B、T轴，计算出平均震源机制解有关参数。

2.2网格搜索法

基于震源机制的网格搜索法是万永革（2012，2015）、Wan等（2016）提出的以震源机制数据为基础来反演应力场的一种算法，此方法基于应力张量在断层面上的滑动方向与剪切应力方向相一致这个准则来求解应力场，并给出在某一置信度下反演参数的置信区间。若研究区有多个不同的震源机制解，则每个解都能给引发断层运动的应力场应力张量一个约束，通过多个解的互相约束就能够获得该区域应力场的平均解。该方法有4大显著优势：一是通过全局网格搜索可反演出最优应力场的解，防止局部陷入极值；二是可对多个震源机制数据赋予各不相同的权重；三是与许忠淮等（1984，1985）滑动方向拟合法所采用的准则相比，该方法对地质上已存在薄弱面而发生的地震的计算准确性更高；四是为检查解的稳定性，除了给出最优解外，还可利用F检验得到给定置信度下应力场反演结果的置信区间，可将主应力轴的可信度和反演结果的可靠性定量地展示出来，这在一定程度上提高了应力场的反演精度。

3结果及可靠性分析

3.1格點尝试法反演结果

笔者利用湖南及其邻区312个地震的529条P波初动极性数据，采用格点尝试法计算得到了研究区平均应力场结果（表2、图2）。从图2可以看出，湖南地区平均震源机制解的2个节面走向、倾角、滑动角依次为4°、55°、78°和204°、36°、106°；P轴方位和倾伏角分别为102°和10°；T轴方位和倾伏角分别为237°和76°；初动符号矛盾比为0.34。

3.2网格搜索法反演结果

基于研究区32个M_L≥2.8地震的震源机制解，笔者应用网格搜索法反演了湖南地区构造应力场，并采用F检验得到了反演参数的估计空间。应力场计算结果及其三维立体图见图3。图3a中黑色弧线代表所选节面的等面积投影，红色大箭头代表P轴的最优方向，蓝色大箭头代表T轴的最优方向，红色小箭头代表断层理论滑动方向，蓝色小箭头代表断层观测滑动方向，红色弧线为最优应力状态下的最大剪应力节面，绿色弧线为得到的90%置信度下应力场的最大剪应力节面，黄色小箭头为该节面的最大剪应力方向，P、B、T周围的封闭曲线代表90%置信度下应力场P、B、T轴的范围，R为应力比值；图3b中红色代表P轴，蓝色代表T轴，U、D分别表示上、下。从表2可见，最优解2个节面的走向、倾角、滑动角依次为3°、50°、81°和197°、41°、101°；通过F检验给出了P、T、B轴90%置信度下的置信区间，P轴方位、倾伏角最优解分别为100°（置信区间为79°～100°）、5°（置信区间为2°～5°），T轴方位、倾伏角最优解分别为225°（置信区间为204°～225°）、81°（置信区间为81°～82°），B轴方位、倾伏角最优解分别为9°（置信区间为-12°～10°）、7°（置信区间为7°～8°）。表中应力比值R=（S₂-S₃）/（S₁-S₃），S₁、S₂、S₃分别表示最大、中间、最小主压应力，表中R=0，表示为纯挤压型。

3.3可靠性分析

从表2可以看出，利用格点尝试法和网格搜索法反演计算得到的湖南地区构造应力场结果比较接近，P、T轴方位、倾伏角等参数相差12°以内，说明两种方法求解结果均可靠。对于网格搜索法，P、T、B轴方位、倾伏角的置信区间数值波动范围较小，在22°以内，反演结果相对稳定。

为了进一步检验结果的可信度，可使用双力偶震源机制最小空间旋转角程序（Kagan，1991）定量计算格点尝试法和网格搜索法求解结果的差异。在空间坐标下2个震源机制解总能够通过旋转特定的角度而达到一致，旋转的角度越小说明2组解差异越小，旋转的角度越大则2组解的差异越大。笔者根据万永革（2008）最小空间旋转角程序，计算格点尝试法反演得到的应力场平均解与网格搜索法反演得到的应力场最优解二者的最小空间旋转角为6.2°，可认为2组解差异很小，一致性好（郑建常，陈运泰，2012），即两种方法得到的结果可信度较高。

4讨论

图2和图3中研究区应力场结果显示：湖南地区P轴优势方位为NWW向，大致垂直于区域内主要断裂。P轴倾伏角接近水平，这与邓起东等（1979）、鄢家全等（1979）、丁旭初和张文涛（1988）、徐纪人等（2008）、陈益明（1992）、谢富仁等（2003）、郭良迁等（2012）、田优平等（2020）的研究结果较为一致，但与蒋维强等（1992）、汪素云和许忠淮（1985）的结果有所差异，这可能是因为之前学者使用的湖南地区资料有限导致计算的结果与本文不同。湖南地区T轴优势方位为NE-NEE向，T轴倾伏角较大。根据Zoback（1992）提出的震源机制类别划分准则，湖南地区平均震源机制解为逆断型，节面走向同区域主断裂方向大致相同；湖南地区总体上受NWW向的挤压应力作用，对该区断裂具有一定的控制，这可能是该区地震多发生在由湘西自治州、娄邵地区和郴州所形成的NW向空间条带的重要原因之一。

华南地块主要受西面的印度板块和欧亚板块碰撞作用及东面的太平洋板块和菲律宾海板块联合俯冲作用的控制（虞廷林，1994；蒋维强等，1992；曹海波，范桃园，2016），内部断裂和活动构造发育，应力场格局复杂多样。湖南地区处于大陆板块内部，作为华南块体的一部分，其区域应力场动力源可能与各板块的相互运动有关。从本文应力场计算结果来看，湖南地区主要受菲律宾海板块NWW向的挤压为主，其次，才受控于太平洋板块向西推挤的影响，西面的印度板块和欧亚板块相互碰撞主要引起青藏高原隆起，加之有云贵高原的阻拦，碰撞产生的影响对湖南地区而言已大幅减弱。综上所述，各方面的综合影响，造就了湖南地区现今构造应力场的基本特征。

5结论

本文采用格点尝试法和网格搜索法反演了湖南地区构造应力场，计算得到P轴和T轴的优势方向，进而推断研究区实际构造应力场的大体方向，主要得出以下结论：

（1）采用格点尝试法计算得到的P轴方位和倾伏角分别为102°和10°，T轴方位和倾伏角分别为237°和76°；采用网格搜索法反演得到的P轴方位和倾伏角分别为100°（置信区间为79°～100°）和5°（置信区间为2°～5°），T轴方位和倾伏角分别为225°（置信区间为204°～225°）和81°（置信区间为81°～82°）。这两种方法计算所得解的最小空间旋转角为6.2°，表明结果可信度较高。

（2）湖南地区平均震源机制解表现为逆断型；主压应力轴优势方位为NWW向，倾伏角近乎水平；主张应力轴优势方位为NE-NEE向，倾伏角较大。

（3）湖南总体上受NWW向的挤压应力作用，對该区断裂具有一定的控制，这可能是该区地震多发生在由湘西自治州、娄邵地区和郴州所形成的NW向空间条带的重要原因之一。

参考文献：

曹海波，范桃园.2016.长江经济带构造应力场特征及动力学环境分析［J］.地质力学学报，22（3）：610-619.

陈益明.1992.华南地区震源机制与应力场特征［J］.华南地震，12（2）：23-31.

邓起东，张裕明，许桂林，等.1979.中国构造应力场特征及其与板块运动的关系［J］.地震地质，1（1）：11-22.

丁旭初，张文涛.1988.中国大陆东部现今构造应力状态［J］.地震学报，10（1）：25-38.

关鹏虎，李斌，李自红，等.2022.多方法求解中小地震震源机制解的可靠性分析——以山西地震带3次中小地震为例［J］.太原理工大学学报，53（2）：289-298.

郭良迁，周海涛，杜雪松，等.2012.中国大陆应变应力场研究［J］.华南地震，32（1）：1-10.

蒋维强，林纪曾，赵毅，等.1992.华南地区的小震震源机制与构造应力场［J］.中国地震，8（1）：36-42.

盛书中，万永革，黄骥超，等.2015.应用综合震源机制解法推断鄂尔多斯块体周缘现今地壳应力场的初步结果［J］.地球物理学报，58（2）：436-452.

田优平，唐红亮，康承旭，等.2020.综合震源机制解法反演湖南地区构造应力场的初步结果［J］.地球物理学报，63（11）：4080-4096.

田优平，余达远，万永革，等.2014.三河—平谷地震区地球物理特征研究［J］.地球物理学进展，29（4）：1563-1572.

田优平，赵爱华.2016.基于小波包和峰度赤池信息量准则的P波震相自动识别方法［J］.地震学报，38（1）：71-85S.

田优平.2015.近震P波震相自动识别方法研究［D］.北京：中国地震局地球物理研究所.

万永革，吴逸民，盛书中，等.2011.P波极性数据所揭示的台湾地区三维应力结构的初步结果［J］.地球物理学报，54（11）：2809-2818.

万永革.2008.美国Landers地震和Hector Mine地震前震源机制与主震机制一致现象的研究［J］.中国地震，24（3）：216-225.

万永革.2012.根据震源机制求解构造应力场的网格搜索法［J］.国际地震动态，（6）：19.

万永革.2015.联合采用定性和定量断层资料的应力张量反演方法及在乌鲁木齐地区的应用［J］.地球物理学报，58（9）：3144-3156.

汪素云，许忠淮.1985.中国东部大陆的地震构造应力场［J］.地震学报，7（1）：17-32.

吴啸龙，向洋，汤伏全.2020.基于GPS应变与震源机制解应力反演喜马拉雅构造带现今地壳形变特征［J］.地球物理学报，63（8）：2924-2939.

谢富仁，崔效锋，赵建涛.2003.全球应力场与构造分析［J］.地学前缘，10（S1）：22-30.

徐纪人，赵志新，石川有三.2008.中国大陆地壳应力场与构造运动区域特征研究［J］.地球物理学报，51（3）：770-781.

许忠淮，戈澍谟.1984.用滑动方向拟合法反演富蕴地震断裂带应力场［J］.地震学报，6（4）：395-404.

许忠淮，阎明，赵仲和.1983.由多个小地震推断的华北地区构造应力场的方向［J］.地震学报，5（3）：268-279.

许忠淮.1985.用滑动方向拟合法反演唐山余震区的平均应力场［J］.地震学报，7（4）：349-362.

鄢家全，时振梁，汪素云，等.1979.中国及邻区现代构造应力场的区域特征［J］.地震学报，1（1）：9-24.

虞廷林.1994.中国东部应力场与板块运动［J］.地震学刊，（2）：13-17.

张培震，邓起东，张国民，等.2003.中国大陆的强震活动与活动地块［J］.中国科学：地球科学，33（S1）：12-20.

鄭建常，陈运泰.2012.基于Langston分解和Hilbert变换约束的区域偏量矩张量反演方法及其应用［J］.地震学报，34（2）：171-190.

Aki K.1966.Earthquake generating stress in Japan for the years 1961 to 1963 obtained by smoothing the first motion radiation patterns［J］.Bull Earthq Res Inst，44（2）：447-471.

Kagan Y Y.1991.3－D rotation of double－couple earthquake sources［J］.Geophys J Int，106（3）：709-716.

Wan Y G，Sheng S Z，Huang J C，et al.2016.The grid search algorithm of tectonic stress tensor based on focal mechanism data and its application in the boundary zone of China，Vietnam and Laos［J］.Journal of Earth Science，27（5）：777-785.

Zoback M L.1992.First－ and second－order patterns of stress in the lithosphere：the world stress map project［J］.J Geophys Res，97（B8）：11703-11728.

Quantitative Results and Confidence Interval Analysis

of the Stress Field in Hunan Region

TIAN Youping SHEN Ping WAN Yongge TANG Hongliang

KANG Chengxu YAO Haidong SHE Xuming YE Shishan

（1.Hunan Earthquake Disaster Risk Prevention Center，Hunan Earthquake Agency，Changsha 410004，Hunan，China）

（2.Institute of Disaster Prevention，Sanhe 065201，Hebei，China）

（3.Hebei Key Laboratory of Earthquake Dynamics，Sanhe 065201，Hebei，China）

（4.Guangdong Earthquake Agency，Guangzhou 510070，Guangdong，China）

Abstract

Based on 529 P－wave polarity data of 312 earthquakes and the focal mechanism of 32 earthquakes with magnitude over 2.8 in Hunan and its neighboring region，we obtain the quantitative results and confidence ranges of the tectonic stress field in Hunan region by using the grid trial method and the grid search method respectively.The mean stress field calculated by the grid trial method shows that the azimuth of P－axis is 102°，the dip angle of P－axis is 10°，and the azimuth and dip angle of T－axis are 237° and 76° respectively.The results from the grid search inversion show that the azimuth and dip angle of P－axis are 100° when confidence interval is 79°-100°，and 5° when confidence interval is 2°-5°，and the azimuth and dip angle of T－axis are 225° when confidence interval is 204°-225°，and 81° when confidence interval is 81°-82°.According to the results of two stress field algorithms，the average focal mechanism proves to be reverse fault in Hunan region.The dominant direction of the principal compressive stress is NWW，and its dip angle is almost horizontal.The dominant direction of the principal tensile stress is NE-NEE，and its dip angle is large.We analyze the reliability of the inversion results from two algorithms，and compare with the previous study，and prove that the results proposed in this paper is of high reliability.

Keywords：stress field；the grid－trial method；the grid－search method；confidence interval；Hunan region