新型装配式干连接自复位结构节点性能理论分析和抗震有限元研究
2023-06-13韩良君葛元辉李延昌梁家栋王荣棋查晓雄
韩良君 李 军 葛元辉 李延昌 梁家栋 王荣棋 查晓雄
(1.深圳市特区建工科工集团有限公司,广东深圳 518034;2.中铁建设集团南方工程有限公司,广东深圳 511400;3.哈尔滨工业大学(深圳)土木工程与环境工程学院,广东深圳 518055)
0 引 言
地震是人类面临的最严重的自然灾害之一,往往会造成不同程度经济损失。因此结构的抗震性能受到专家学者的高度重视。设计出抗震性能优异的结构体系,是专家学者和结构工程师的目标。我国是全球大陆地震活动最活跃的地区之一,地震活动具有频率高、强度大、震源浅和分布广等特点。20世纪我国发生7级以上地震116次,约占全球6%,其中大陆地震71次,约占全球大陆地震29%[1]。因此,保证结构的安全性以及良好的震后性能,对人民的生命财产和社会经济发展具有重要意义。
混凝土框架结构是常见的抗震结构体系之一,广泛应用于抗震设防地区中。传统混凝土框架的抗震设计采用基于延性的设计理念,通过结构自身的塑性变形来消耗地震能量,避免结构在地震中倒塌,保护生命和财产安全。然而,采用该理念设计出来的结构在地震后存在较大的结构损伤和残余变形,震后修复困难,导致巨大的经济损失。Miranda通过研究,指出传统延性结构震后残余变形对经济损失影响最大,在设防烈度下,传统延性结构虽能够保证大概率不倒塌,但结构往往因为震后残余变形过大,需重新建造而造成巨大经济损失[2]。2011年,新西兰基督城发生里氏震级6.3级的大地震,中央商务区近一半的建筑物由于产生了严重损伤而无法正常使用,近1 000栋建筑物被拆毁,地震后的重建费用预计高达400亿新西兰元[3]。震后高额的重建费用说明当前抗震设计规范中基于延性的设计理念和保障人民生命安全为主的设计目标,仅能保证建筑结构在设计地震作用下不发生倒塌,缺乏对结构震后性能的考虑。随着社会经济发展水平提高,人们对抗震结构的性能也提出了更高的要求,设计出在设防地震作用下不破坏或可快速修复的抗震结构体系,成为当前地震工程领域研究热点之一。
近年来,自复位功能结构作为一种新型的减震控制结构,引起了工程师和专家学者的广泛关注。自复位结构不仅能在地震发生时保护人们的生命财产安全,也有助于震后修复,恢复正常生产生活,是结构抗震设计的一个新方向[4]。研究[5-6]表明,结构的摇摆可以降低地震作用和结构自身的延性需求,减少地震破坏,降低震后修复费用。通过放松结构与基础间或梁柱间的约束,使结构与基础或构件接触面处仅承受压力作用而无拉力作用,在地震作用下结构发生摇摆,施加预应力使结构复位,形成自复位结构,如图1所示。这种新型结构体系能够有效控制结构震后残余变形,减少修复时间成本和经济成本。
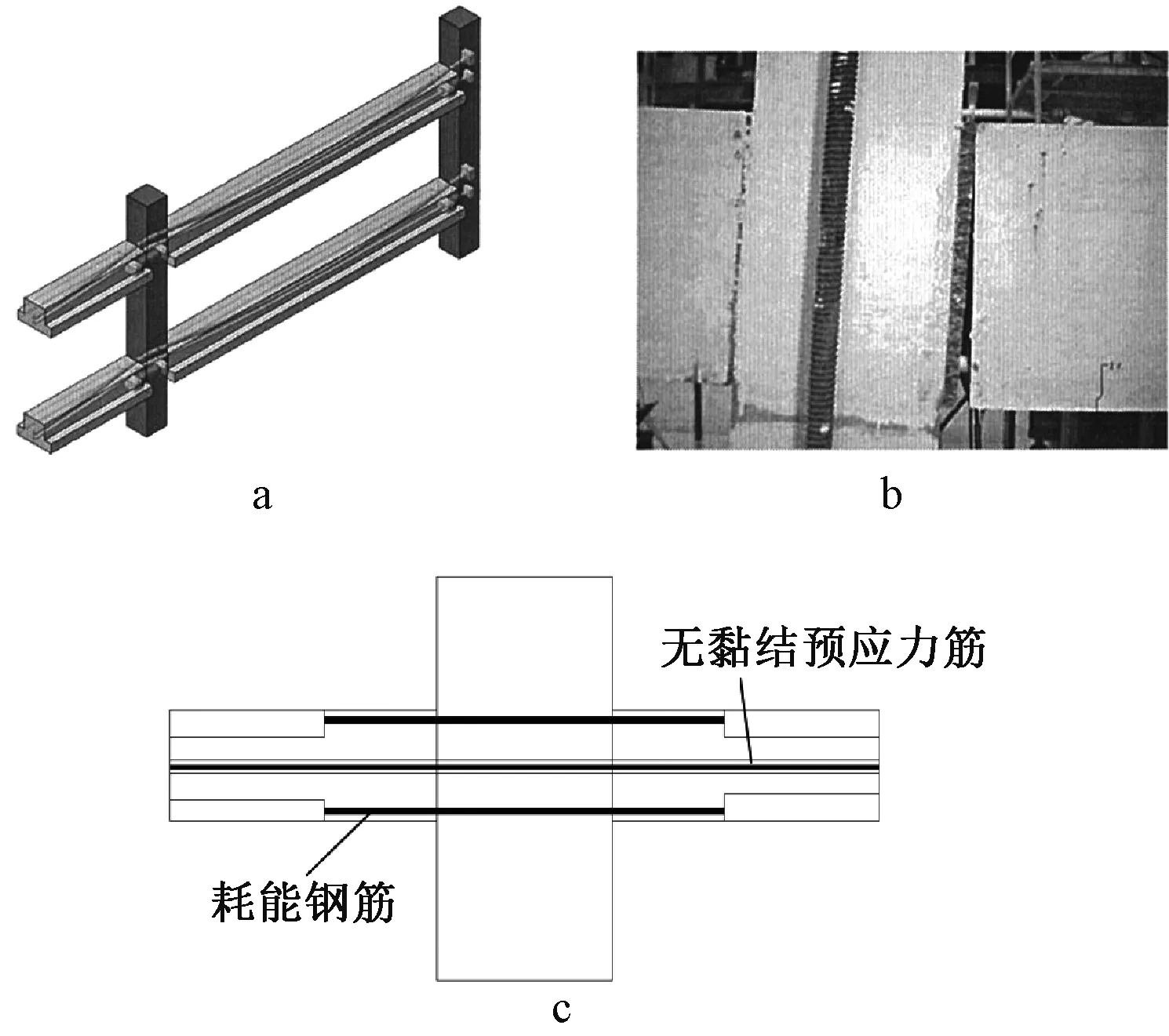
a—自复位摇摆框架;b—自复位摇摆节点震后状态;c—自复位摇摆节点构造。图1 自复位摇摆结构Fig.1 Self-centering swing structure
对提出的新型自复位装配式干连接节点形式,采用ABAQUS有限元模拟软件进行建模,研究新型自复位装配式干连接节点性能。
1 节点构造及组成
在装配式螺栓连接节点的基础上,结合自复位节点的特点,提出一种基于自复位性能的新型装配式干连接自复位节点(简称“干连接自复位节点”),如图2所示[7]。该新型节点与摩擦耗能自复位节点相比,具备耗能机制可控、耗能件安装精度要求较低、施工速度快的优点;与阻尼器耗能自复位节点相比,具备构造简单、费用成本低、施工方便等优点。
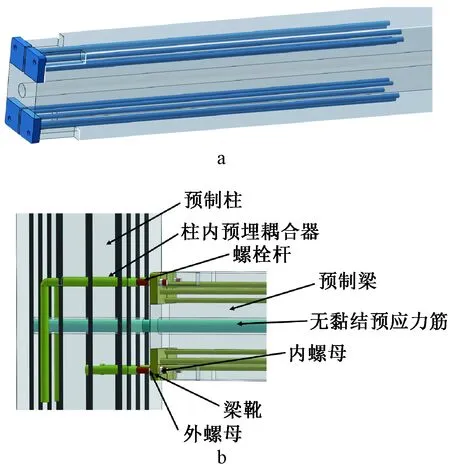
a—梁侧立面;b—节点正立面。图2 新型干连接自复位节点[7]Fig.2 New dry connection self-centering node
干连接自复位节点现场施工顺序为:首先将梁柱的孔洞对齐,4个外螺母分别放置在梁靴外部;接着将螺栓杆包裹塑料或涂油的方式插入到梁靴孔洞内(目的是形成无黏结段),旋转螺栓,直至插入到柱内预埋耦合器中;接下来在梁靴内部放置螺母并拧紧外螺母与内螺母,使得梁靴相对螺栓杆位置固定,地震时利用螺栓杆拉压屈服来消耗能量;最后在接缝处灌浆,张拉无黏结预应力筋[7]。
节点基本参数为:梁长度7.5 m,梁截面尺寸650 mm×400 mm,柱高3.8 m,柱截面尺寸700 mm×700 mm,混凝土强度等级为C50,节点弯矩设计值为611 kN·m。按照文献[7]提出的方法,初选自复位比λ=1.25进行节点设计,可以确定干连接自复位梁截面由10根截面面积143.3 mm2的钢绞线来施加总共1 517 kN的初始预拉力,以提供自复位能力;4根直径39 mm的螺栓提供耗能能力,对应的梁截面配筋如图3所示,设计后节点自复位比λ=1.22,节点弯矩承载力为767 kN·m[7]。
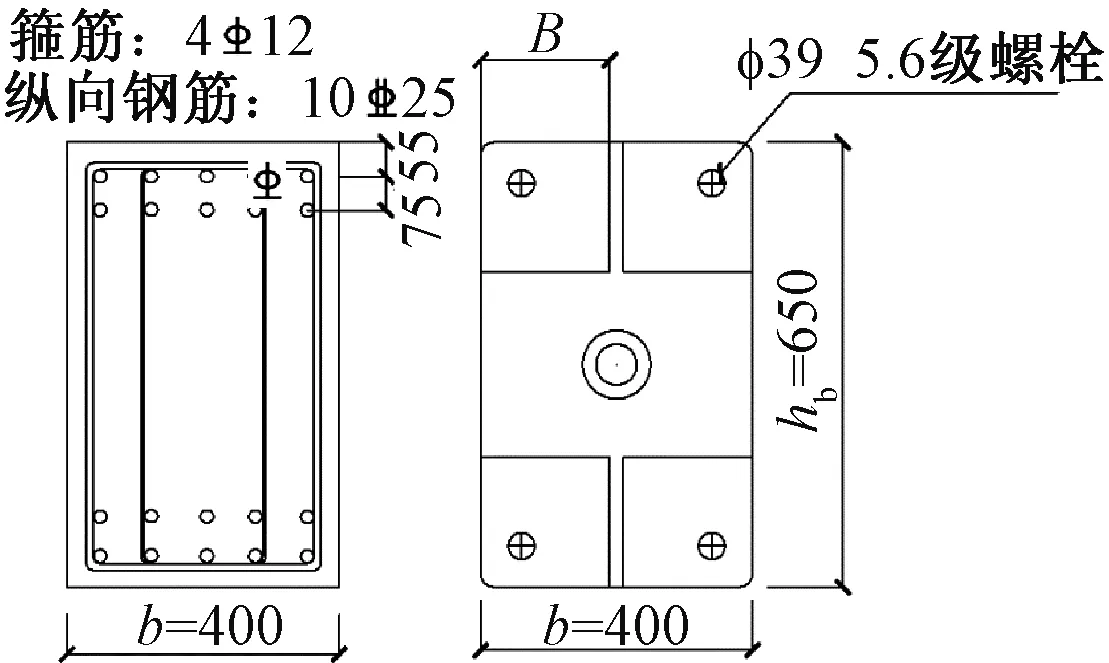
图3 梁截面配筋图[7] mmFig.3 Beam section reinforcement diagram
由于梁柱节点在地震作用下会打开,造成单个跨度上梁的伸长,若采用传统意义的固接楼板,会对楼板产生水平方向的拉力,导致楼板开裂,同时限制干连接自复位节点的打开,影响结构的自复位性能。因此在干连接自复位节点的楼板处理中,将楼板与梁柱在连接处断开,当梁柱节点打开时,楼板也随之打开运动,消除楼板对梁柱节点打开的约束作用。
2 节点性能有限元验证
2.1 建立模型
为研究装配式干连接自复位节点性能,建立相应有限元模型,如图4所示。通过有限元模拟,将装配式干连接自复位节点和现浇节点进行对比,分析二者性能差异;同时对装配式干连接自复位节点进行参数分析,得到装配式干连接自复位节点性能的影响因素。为了方便加载及后张无黏结预应力筋的设置,在梁一端设置加载端头,构件的尺寸与设计梁柱节点的尺寸保持一致。
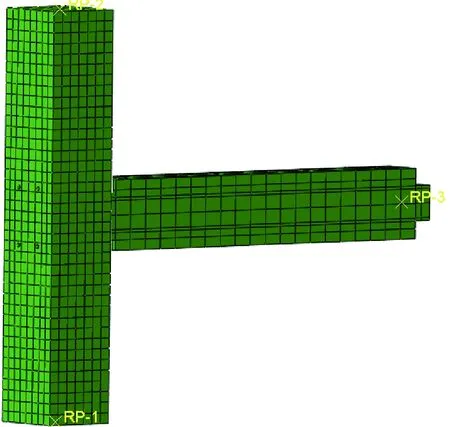
图4 装配式干连接自复位节点有限元模型Fig.4 Finite element model of self-centering joint of assembled dry connection
2.1.1简化及计算假定
节点模型建模分析时进行如下简化和假定:1)不考虑试件的初始几何缺陷和残余应力;2)耗能螺栓仅对使用情况进行理论阐述,不作具体的受力分析,建模时简化为螺杆,且螺纹处的应力、应变状态不是研究重点,因此不对螺纹精细建模;3)建模时忽略螺栓孔与螺杆之间的空隙,螺孔与螺栓直径相同;4)为方便接触设置,本文建模时螺栓和耦合器设置为同一部件。
2.1.2单元设置及网格划分
节点模型主要包括:预制混凝土梁柱、梁靴、螺栓(耦合器)、梁柱钢筋、预应力筋。其中预应力混凝土梁柱、梁靴、螺栓均采用C3D8R实体单元进行模拟。梁柱钢筋、预应力筋均采用T3D2桁架单元进行模拟。混凝土梁柱网格尺寸为150 mm,螺栓,梁靴网格尺寸为10 mm,对梁靴的螺栓孔进行适当加密处理。
2.1.3约束和接触的定义
模型中梁柱的普通钢筋由纵筋和箍筋合并成一个整体,以增强钢筋笼的整体工作性能,然后将钢筋单元嵌入整体模型中,不考虑钢筋与混凝土之间的黏结滑移。耗能螺栓一部分内置到柱中,一部分与梁靴的螺栓孔内壁采用Tie进行绑定,保证受力时各部件的变形一致,并在螺栓上设置无黏结段来耗能。
梁柱节点开缝面的模拟是有限元模拟的关键之处,由于干连接自复位节点处以受弯为主,假定梁柱截面连接部分可以提供足够的抗剪能力,防止梁发生侧向平移和沿着位移加载发生自由抬升。Kurama采用ABAQUS中“gap/contact”单元来模拟开缝面的特性[8]。在本文中,梁与柱接触面属性法线方向,定义为“Hard contact”,允许接触后产生分离;切线方向定义为“Rough”,接触后不产生相对滑移。采用这种接触方式不考虑接触界面上混凝土竖向受拉强度。由于混凝土受拉强度与钢筋受拉强度相比很小,所以这种定义是合理的。
预应力筋与混凝土之间无黏结效应的模拟是先建立有黏结预应力筋的模型,提交作业,再次导入inp文件,预应力筋的端点与梁柱端点采用MPC梁的约束,模拟实际中无黏结预应力筋与梁柱端协同变形;将预应力筋网格中的节点与梁柱网格节点采用Coupling约束进行设置,同时释放预应力筋方向上的约束来模拟实际情况中后张预应力筋与梁柱的无黏结状态,如图5所示。
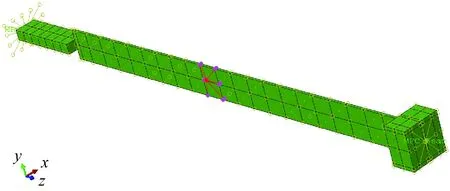
图5 无黏结预应力的有限元模拟Fig.5 Finite element simulation of Unbonded Prestress
对于初始预应力的施加,ABAQUS提供了多种模拟方法,包括MPC方法、等效降温法、ABAQUS自带的初始应力法、装配荷载法等。本文采用等效降温法模拟初始预应力。等效降温法从材料自身的热胀冷缩特性实现预应力效应,即对预应力筋施加一个温度场变量后,预应力筋收缩,从而有效模拟预应力筋张拉过程。施加的温度场变量采用式(1)进行计算。
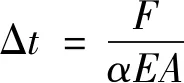
(1)
式中:Δt为所需施加的温度场变量;F为预应力筋施加的预张力;α为预应力筋的膨胀系数;E为预应力筋的弹性模量;A为预应力筋的面积。
2.2 节点有限元模型有效性验证
为验证采用本文建模思路建立的有限元模型的准确性,选取文献[9-10]中的JH1模型试验结果进行对比验证,按照本文的建模思路,建立文献中滞回试验的有限元模型,如图6所示。
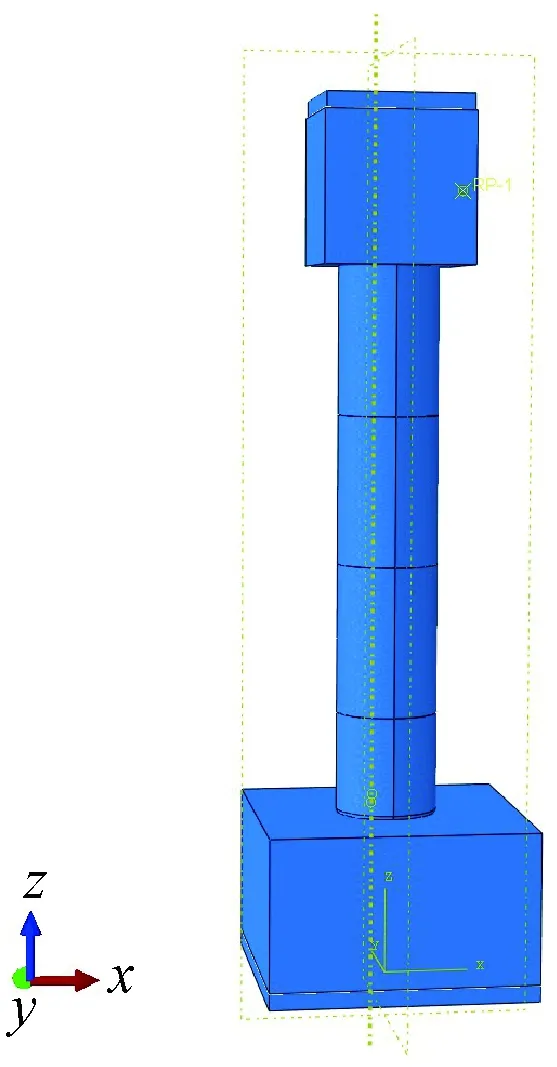
图6 文献[9-10]中滞回试验的有限元模型Fig.6 Reference [9-10] hysteretic test finite element model
对该模型进行滞回模拟,为更直观进行对比分析,选取最外圈滞回曲线进行对比分析,有限元模拟和试验的最外圈滞回曲线如图7所示。可以看出:有限元模拟曲线与试验曲线拟合度较好,验证了采用本文有限元建模思路建立的有限元模型的有效性。
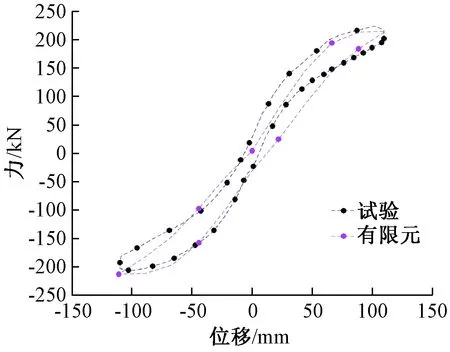
图7 力-位移曲线Fig.7 Finite element curve and test curve
2.3 节点单调加载
2.3.1荷载-位移曲线
对干连接自复位节点(JD)进行了单调加载的数值模拟分析,为了验证自复位连接节点是否满足工程中节点刚性需求,建立相同尺寸的现浇节点(XJ),不设置预应力筋,得到了节点单调加载下的F-Δ曲线,如图8所示。
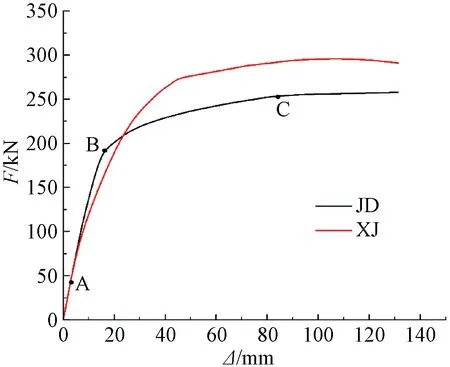
图8 节点试件的荷载-位移曲线Fig.8 Load-displacement curves of joint specimen
从节点单调加载的荷载-位移曲线可知:从原点到A点,干连接自复位节点的整体刚度几乎不变,说明在A点之前梁柱还未打开,通过预应力筋的后张预应力作用使节点的初始刚度与现浇节点相同;AB段节点在外荷载作用下开始张开,这时节点的抗弯刚度主要由螺栓和预应力筋来提供,当达到B点时,螺栓开始受拉屈服;AB段现浇节点刚度小于干连接自复位节点,因为此时耗能螺栓还未屈服,节点刚度由螺栓和预应力筋贡献,而现浇梁柱节点已经产生塑性变形,混凝土开始有损伤累积,导致现浇节点的承载力小于干连接自复位节点;B点之后,干连接自复位节点刚度突然减小,代表螺栓已经屈服,此时节点的抗弯刚度主要由预应力筋提供,刚度小于现浇节点,继续加载至C点,直至节点极限承载力,预应力筋屈服。
根据节点单调加载曲线中的A点,可以计算出节点打开过程中压力为0时的零压弯矩为171.78 kN·m,理论计算的零压弯矩为164.36 kN·m;根据文献[7]的分析结果,节点有限元模拟的承载力为794 kN·m,自复位比为λ=1.21,表明有限元模拟结果与理论计算结果基本吻合,说明有限元建模能够较好模拟节点的破坏状态及受力状态。
2.3.2单调加载节点应力分布及破坏机理
节点单调加载至破坏状态时现浇与干连接自复位梁柱节点应力及损伤云图如图9所示。可以看出:对于现浇节点的破坏模式是梁柱混凝土部分形成塑性铰;而干连接自复位节点损伤主要集中在混凝土梁的受压区。因为放松梁柱节点处的约束,可利用摇摆截面的螺栓塑性变形来消耗能量,一部分损伤由螺栓代替,所以干连接自复位的混凝土塑性损伤明显小于现浇节点。

a—现浇节点Mises应力云图,MPa;b—现浇节点混凝土塑性损伤云图;c—干连接自复位节点Mises应力云图,MPa;d—干连接自复位节点混凝土塑性损伤云图。图9 节点的Mises应力云和混凝土塑性损伤云图Fig.9 Nephograms of Mises stress and concrete plastic damage of joints
节点螺栓的塑性应变云图如图10所示。可以看出:现浇节点内置螺栓的塑性应变明显小于干连接自复位节点,因为在外荷载作用时,干连接自复位节点耗能螺栓首先屈服来消耗地震能量,从而减小混凝土的损伤,做到节点损伤位置可控,而螺栓在实际工程中是可以更换的,有效降低结构震后修复成本。
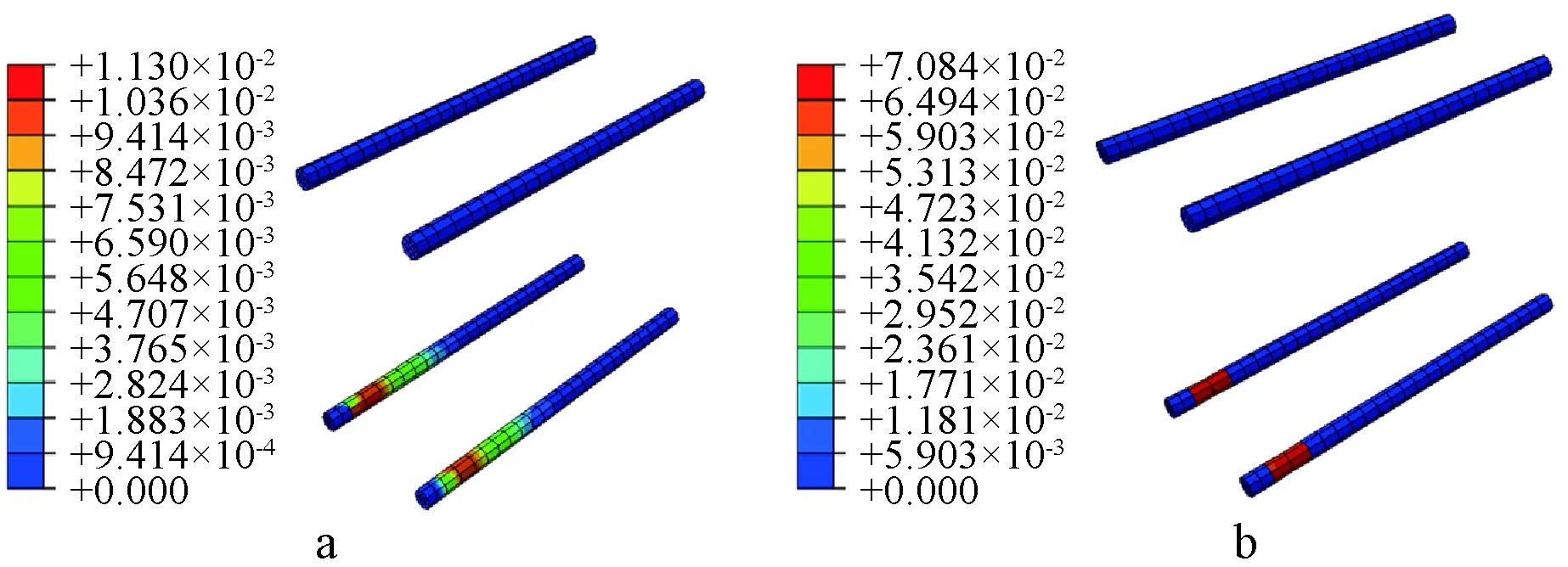
a—现浇节点;b—干连接自复位节点。图10 节点螺栓塑性应变云图Fig.10 Nephograms of plastic strain of joint bolt
2.3.3初始预应力对节点力学性能的影响
为探究初始预应力对节点破坏模式和转动刚度的影响,以自复位节点模型JD为基础,选取不同初始预拉力Tpt,initial=1 000,2 000 kN的节点,命名为JD-T1和JD-T2,分别进行单调加载有限元模拟,得到节点的F-Δ曲线,如图11所示。可以看出:随着初始预拉力Tpt,initial的增大,节点的零压弯矩Mdec有一定的增大,但不明显;从节点脱开到螺栓屈服的这一过程中,随着初始预拉力Tpt,initial的增大或减小,节点刚度也相应地增大或减小,但都大于现浇节点刚度。这是因为初始预拉力Tpt,initial的增大,约束了节点处变形,需要更大的外荷载才能使螺栓屈服,这也证明此阶段干连接自复位节点的刚度主要由预应力筋和螺栓来提供;螺栓屈服后,节点的刚度只由预应力筋提供,图11中曲线后半部分几乎是平行上升也证明了这一点。

图11 不同初始预应力节点的荷载-位移曲线Fig.11 Load-displacement curves of different initial prestressed joints
根据图11、图12可以计算出JD-T1和JD-T2有限元模拟的节点零压弯矩Mdec、节点自复位比λ和节点承载力Mn,将其与理论计算结果对比,汇总于表1中。可看出:有限元模拟结果与理论计算结果基本吻合,说明有限元建模能够较好模拟节点的破坏状态及受力状态。

表1 不同初始预应力节点力学性能的理论计算值与有限元计算值对比分析Table 1 Comparative analysis of theoretical and finite element calculation values of mechanical properties of different initial prestressed joints

a—JD-T1梁截面;b—JD-T2梁截面;c—JD-T1螺栓;d—JD-T2螺栓;e—JD-T1预应力筋;f—JD-T2预应力筋。c为等效受压区高度。图12 不同初始预应力节点部件应力云图 MPaFig.12 Stress cloud diagram of components at different initial prestressed nodes
根据图13、图14可知:增加预应力筋的初始预拉力,节点受压区混凝土损伤也随之增大,耗能螺栓的塑性应变也随之增加。这是因为随着初始预拉力增大,节点抗弯承载力会有显著提升,螺栓受力也随之增大,需要更高的混凝土受压区参与受力,导致混凝土损伤增大。因此,实际工程中设计自复位节点不能过分追求自复位性能而加大初始预应力,有可能会导致预应力筋屈服前受压区混凝土被压碎。
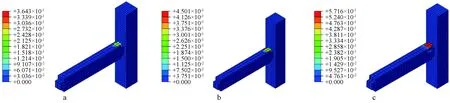
a—JD-T1;b—JD;c—JD-T2。图13 不同初始应力节点混凝土塑性损伤云图Fig.13 Nephogram of plastic damage of concrete at joints with different initial stresses
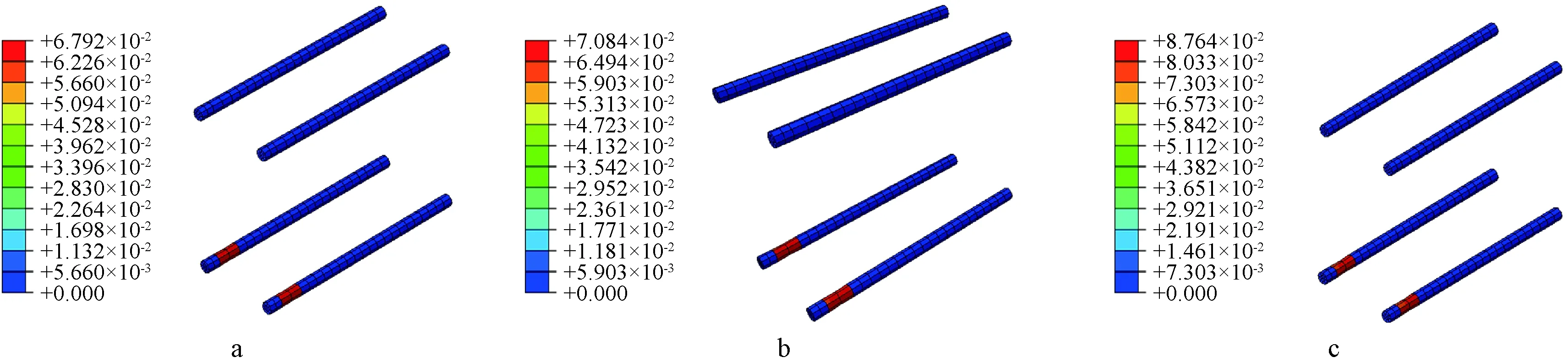
a—JD-T1螺栓;b—JD螺栓;c—JD-T2螺栓。图14 不同初始应力节点螺栓塑性应变云图Fig.14 Cloud diagram of plastic strain of bolts at nodes with different initial stresses
2.3.4螺栓强度对节点力学性能的影响
为探究螺栓强度对节点破坏模式和转动刚度的影响,以节点模型JD为基础,选取不同的螺栓屈服强度,分别为fy=240,480 MPa,命名为JD-L1和JD-L2分别进行单调加载数值模拟,得到节点的荷载-位移曲线,如图15所示。可以得知:随着耗能螺栓强度等级增加,节点承载力显著提升;在加载初期,3种自复位节点的荷载-位移曲线完全重合,代表3种节点具有相同的节点打开弯矩;节点打开后到螺栓屈服前,3种节点的抗弯刚度也相同,这是因为节点的初始预应力相同,只是螺栓的屈服强度不同,螺栓规格、弹性模量都一致,故曲线在加载初期完全重合,区别在于节点的屈服点不同,节点屈服后,3条曲线几乎平行上升,这阶段节点的刚度只由预应力筋提供;当位移达到100 mm时,对于现浇节点,节点的曲线开始下降,代表节点已经开始破坏,而对于自复位节点,只要预应力筋不失效,节点的承载力不会降低。
根据图15、图16可以计算出JD-L1和JD-L2有限元模拟的节点自复位比λ和节点承载力Mn,并将其与理论计算结果对比,汇总于表2。可看出:有限元模拟结果与理论计算结果基本吻合,说明有限元建模能够较好模拟节点的破坏状态及受力状态。
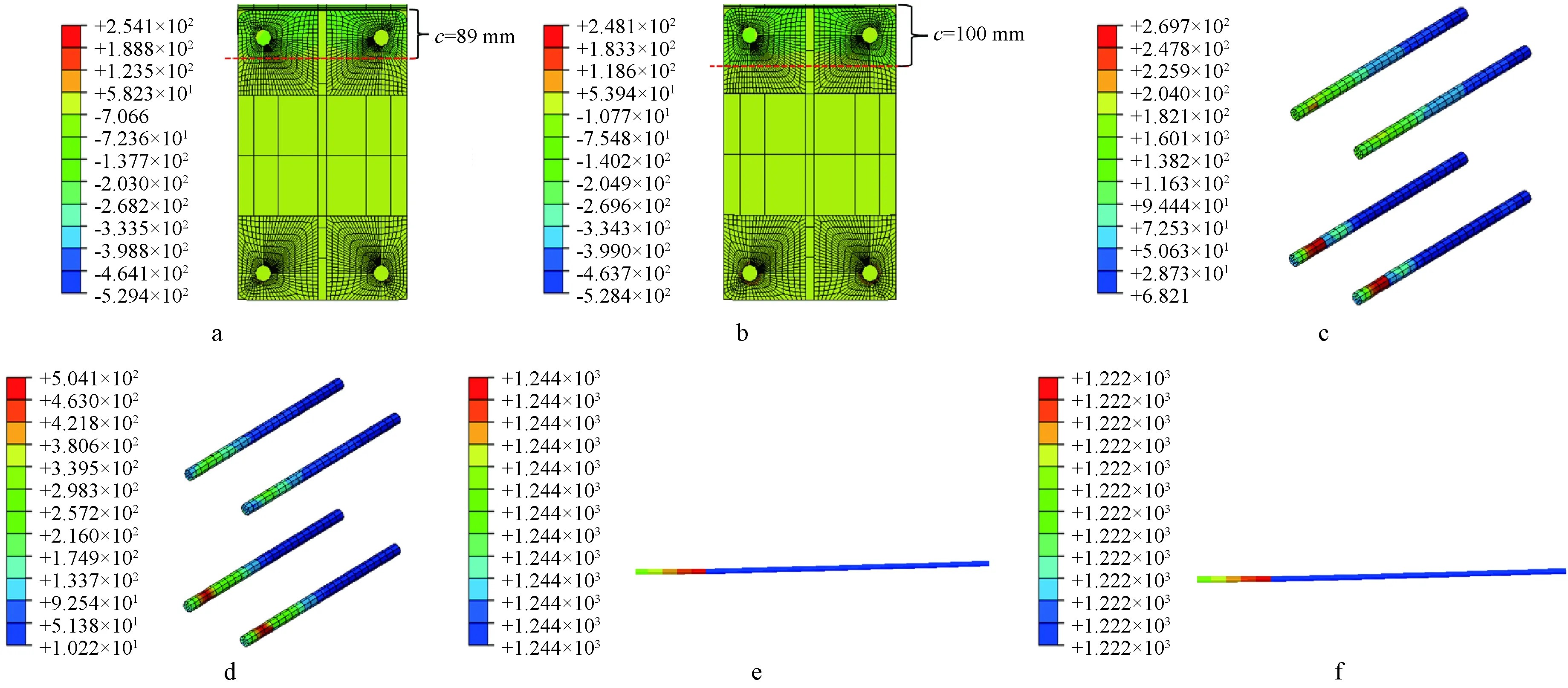
a—JD-L1梁截面;b—JD-L2梁截面;c—JD-L1螺栓;d—JD-L2螺栓;e—JD-L1预应力筋;f—JD-L2预应力筋。图16 不同螺栓强度节点部件应力云图 MPaFig.16 Stress cloud diagram of components at different bolt strength nodes

表2 不同螺栓强度节点力学性能的理论计算值与有限元计算值对比分析Table 2 Comparative analysis of theoretical and finite element calculation values of mechanical properties of different bolt strength joints
不同螺栓强度节点的混凝土塑性损伤云图及螺栓塑性应变云图如图17a~c、图18所示。可以看出:达到设计位移时,随着螺栓强度等级增加,节点受压区混凝土塑性损伤逐渐减小,这是因为螺栓强度等级增加,螺栓对截面弯矩贡献增加,且螺栓的塑性变形增大,螺栓耗能能力增强,能消耗更多地震能量,保护主体结构,所以混凝土塑性损伤减小。如图17d~f所示,到达加载后期,JD-L2节点的塑性损伤明显大于其他两个节点,这是因为采用6.8级螺栓延性较其他两个螺栓好,能够产生较大的塑性变形,屈服应力较大,需要更高的受压区高度保持截面平衡,导致混凝土产生更大的压力,所以混凝土塑性损伤较高。因此,增加螺栓屈服强度,会增加节点的耗能能力,但会使得节点延性有所下降。
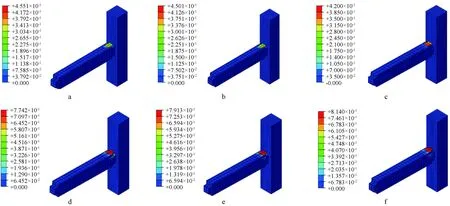
a—JD-L1混凝土;b—JD混凝土;c—JD-L2混凝土;d—加载后期JD-L1混凝土;e—加载后期JD混凝土;f—加载后期JD-L2混凝土。图17 同螺栓强度节点混凝土塑性损伤云图Fig.17 Nephograms of concrete plastic damage of joints with different bolt strength

a—JD-L1螺栓;b—JD-L2螺栓。图18 不同螺栓强度节点螺栓塑性应变云图Fig.18 Cloud diagrams of bolt plastic strain of joints with different bolt strength
2.4 节点抗震性能
2.4.1加载曲线
低周往复荷载的加载制度根据ATC-24(1992)[11]的建议:试件的加载采用位移控制,分别按照0.25Δy、0.5Δy、0.7Δy进行加载;试件屈服后,采用1.0Δy、2.0Δy、3.0Δy、5.0Δy、6.0Δy进行加载。试件屈服前的三级,每级循环2圈,试件屈服后各级,前面三级(1.0Δy、2.0Δy、3.0Δy)循环3圈,其余的循环2圈,加载制度如图19所示。
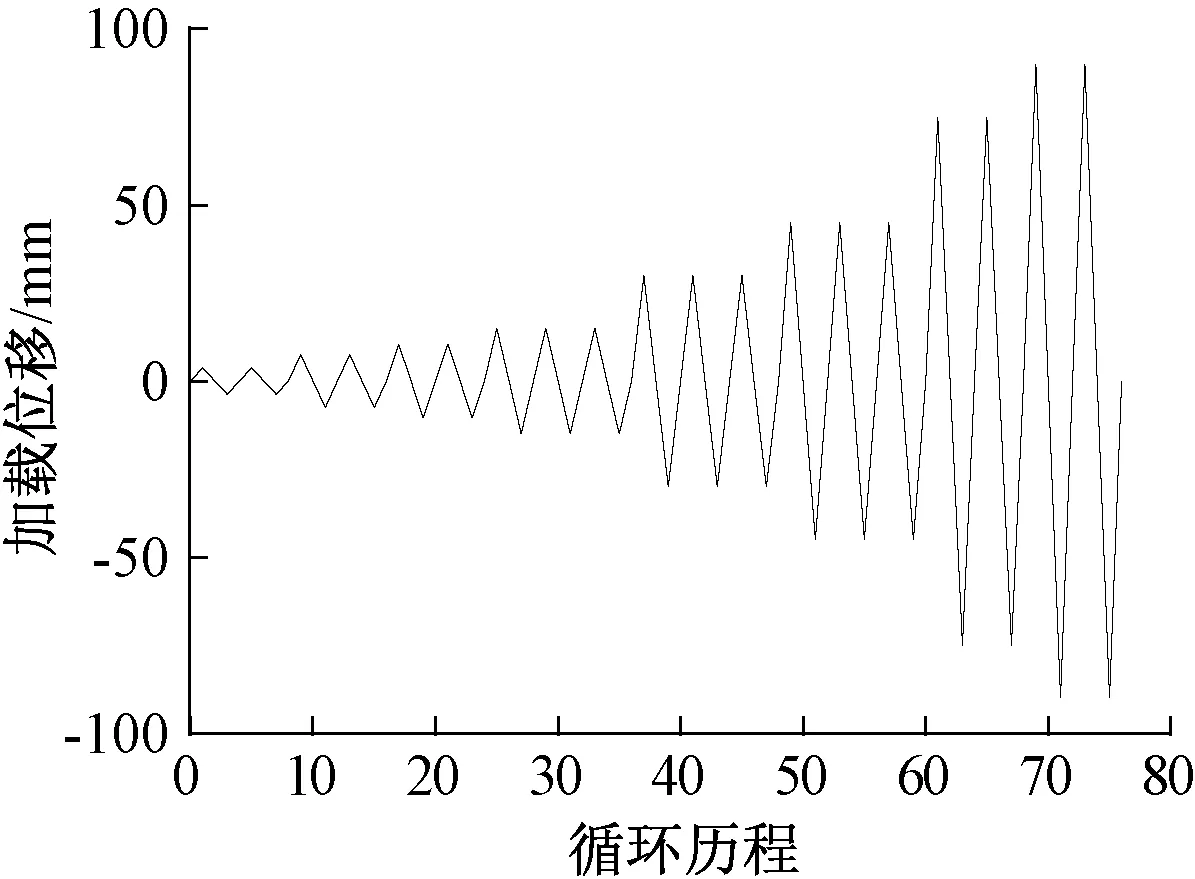
图19 加载制度Fig.19 Loading system
2.4.2节点滞回曲线与损伤云图
为了更好地分析干连接自复位节点抗震性能,对现浇节点和干连接自复位节点进行滞回分析,分别提取了现浇节点(XJ)和干连接自复位节点(JD)模型的滞回曲线,如图20所示。可以看出:现浇节点的滞回曲线呈现饱满的梭形,具有良好的耗能能力,但当力为零时,现浇节点的位移并不为零,说明现浇节点残余变形较大;干连接自复位节点滞回曲线的滞回环相对饱满,说明干连接自复位节点也具有良好的耗能能力;同时与横坐标轴交点数值较小,代表节点的残余变形得到有效控制。理论上当节点自复位比λ大于1时,节点应没有残余变形,这是因为理论只考虑了预应力筋与螺栓的相对关系。在实际加载过程中,梁混凝土不可能完全不受力,梁靴和混凝土共同受压,混凝土也会产生塑性变形(塑性损伤),在滞回加载初期,混凝土还未产生塑性变形,节点具备完全的自复位性能,但在加载后期,混凝土产生塑性损伤,所以加载后期自复位节点不能实现完全恢复。
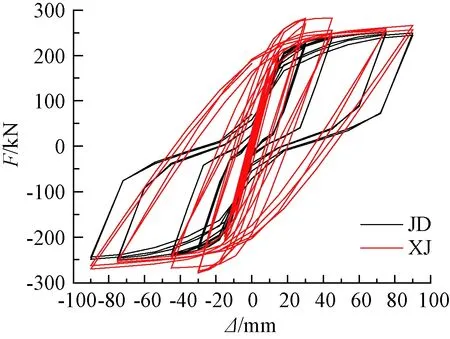
图20 节点滞回曲线Fig.20 Joint hysteretic curves
如图21所示,现浇节点处混凝土发生较大的损伤,破坏机制为梁柱产生塑性铰发生破坏。对于干连接自复位节点,只在梁端产生少量混凝土塑性损伤,柱节点部位几乎无损伤,破坏机制为预应力筋受拉屈服,可见干连接自复位节点能够有效地控制节点处的塑性损伤。
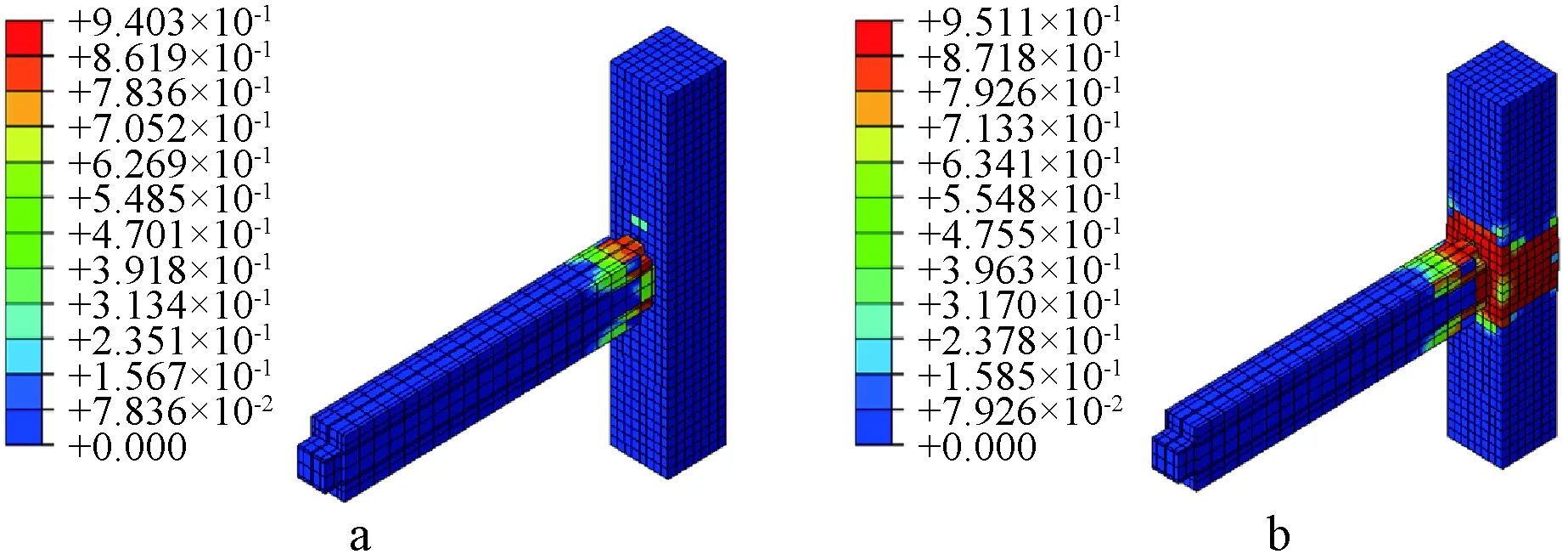
a—现浇节点;b—干连接自复位节点。图21 节点混凝土塑性损伤云图Fig.21 Nephograms of plastic damage of joint concrete
2.4.3初始预应力对节点抗震性能的影响
为了分析初始预应力对干连接自复位节点的滞回性能的影响,分别提取了JD-T1、JD-T2的滞回曲线,如图22所示。滞回环的面积大小表征节点耗能能力,滞回环面积越大耗能能力越强,滞回环面积越小则耗能能力越弱。可以看出:增大节点的初始预应力,节点自复位比增大,节点的残余变形越来越小,但节点的耗能能力也随之减小。
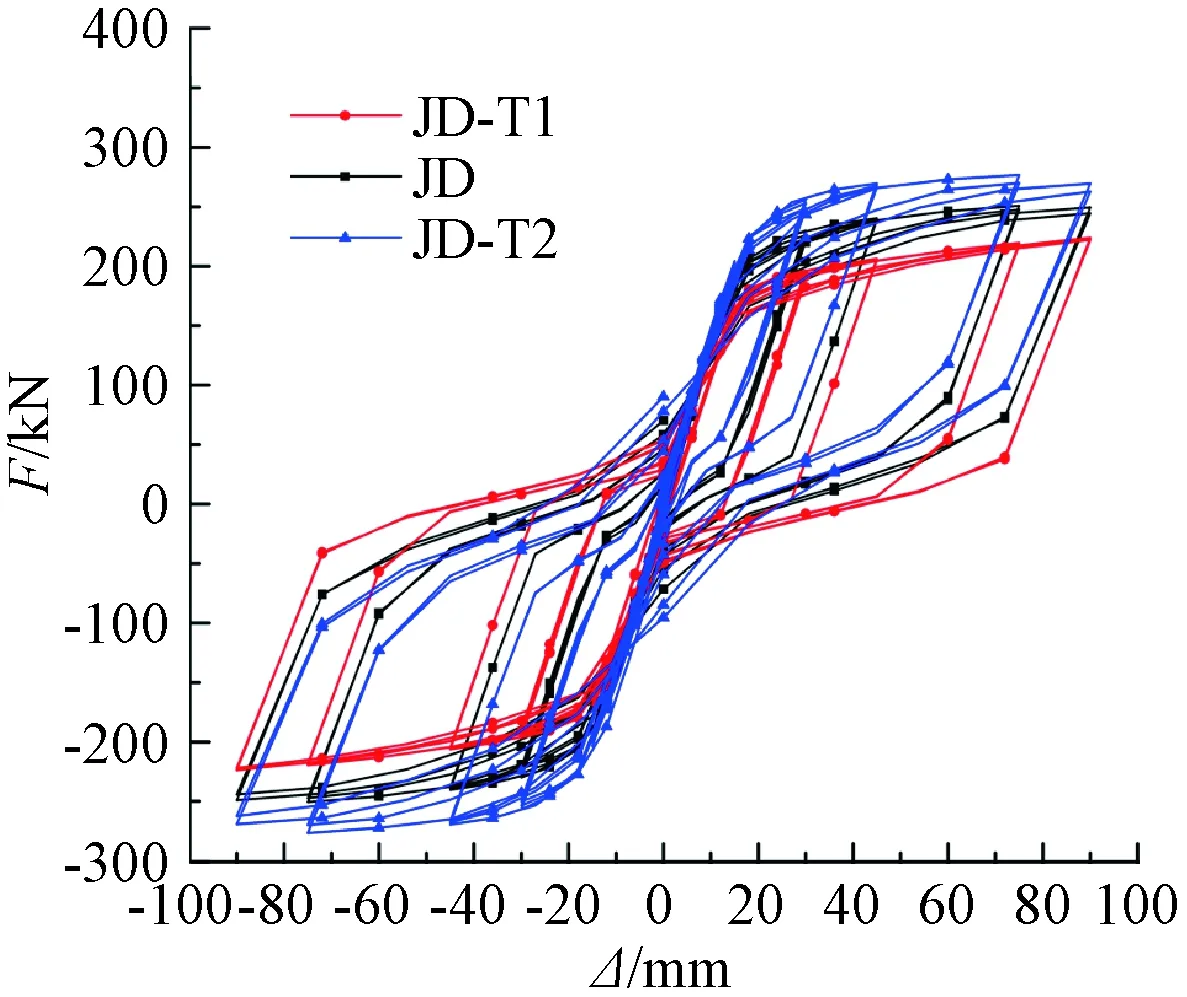
图22 不同初始预应力节点滞回曲线Fig.22 Hysteretic curves of different initial prestressed joints
2.4.4螺栓强度对节点抗震性能的影响
为了分析螺栓强度对自复位节点的滞回性能的影响,分别提取了JD-L1、JD-L2的滞回曲线,如图23所示。可以看出:随着螺栓强度的增加,节点自复位性能逐渐减弱,但耗能能力增强。在加载级数较小时,JD-L1的累计耗能最大,这是因为JD-L1螺栓屈服强度低,螺栓率先屈服开始耗能;但随着加载级数的增加,JD-L2耗能的优势开始显现出来,累计耗能逐渐增加。随着位移的增大,各试件累计耗能随之增加。
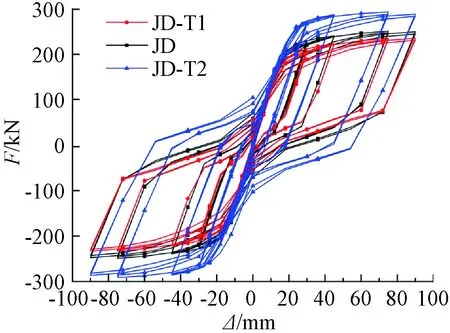
图23 不同螺栓强度节点滞回曲线Fig.23 Hysteretic curves of joints with different bolt strength
3 结束语
针对提出的新型干连接自复位节点形式,采用有限元软件ABAQUS对新型干连接自复位节点进行单调加载和低周往复荷载作用下的数值模拟,对节点的应力分布、破坏机理及抗震性能进行了分析,研究了节点的滞回性能、刚度退化、耗能性能,得到以下主要结论:
1)干连接自复位节点与现浇节点具有相当的初始刚度。现浇节点的破坏模式是梁柱混凝土部分形成塑性铰,而新型干连接自复位节点的损伤云图主要集中在梁受压区,表明除受压区混凝土轻微剥落以外,主体结构无失效性损伤,保证结构可快速修复投入正常使用。
2)放松梁柱节点处的约束,可利用摇摆截面的螺栓塑性应变来消耗能量,且很大一部分损伤由螺栓承担,所以干连接自复位的混凝土塑性损伤明显小于现浇节点,保证损伤可控。
3)提升节点的初始预应力大小,有利于提升节点的零压弯矩、节点的抗弯承载力和自复位比,但混凝土的塑性损伤也随之提高;随着螺栓强度的增加,节点的承载力随之增加,但在加载后期,混凝土损伤也相对低屈服点螺栓严重。
4)从节点的滞回曲线可以看出,干连接自复位节点与现浇节点相比,具备相当的耗能能力,同时干连接自复位节点残余变形小于现浇节点,实现了震后自复位。
5)随着初始预应力的增加,节点的自复位性能提高,但节点的耗能能力和延性都有所下降;随着螺栓强度等级提升,自复位性能下降,节点耗能能力提升,但节点延性下降。
