基于有限条带法的高强钢筋-超高性能混凝土构件受弯性能分析

2023-06-13李志远杨家琦王月桂李映春侯普民

工业建筑 2023年3期

胡利李志远杨家琦王月桂李映春侯普民

(1.中国人民解放军军事科学院国防工程研究院,北京 100085;2.清华大学,北京 100084;3.中国矿业大学(北京),北京 100083)

超高性能混凝土(UHPC)是一种具有超高强度、超高耐久性和超高韧性的新型水泥基复合材料,以其出色的力学性能和耐久性能受到了广泛关注,近年来在实际工程中也得到了一定的推广,具有良好的应用前景。在材料组成上,UHPC基材是将毫米级的骨料、微米级颗粒(水泥、粉煤灰、矿粉等)和亚微米级活性材料(硅灰),基于最大堆积密度理论进行配比,形成致密的水泥基材料。在UHPC基材中掺入随机分布的金属纤维(一般为钢纤维)或有机纤维,可以提高材料的强度和韧性,并产生一定的应变硬化行为。对于此类材料,各国称谓不一,如超高性能纤维材料混凝土、活性粉末混凝土等,也有学者仍沿用UHPC称谓。文中将UHPC定义为钢纤维增强的超高性能混凝土。

由于水泥基体的致密性及钢纤维的作用,UHPC具有良好的耐久性、耐磨性和抗冲击性,力学性能相比于普通混凝土有极大的提升,抗压强度可达到约200 MPa,抗拉强度可达到10 MPa,且韧性强,受拉时可产生一定的应变硬化效应。目前学术界对于UHPC单轴应力-应变行为已经有了较多的研究[1-7],并提出了多种UHPC单轴受压、受拉应力-应变曲线,为UHPC构件的分析提供了理论基础。UHPC广泛应用于桥梁工程、组合结构、结构修复加固、叠合构件拼装等[8-14]。同时,由于其强度高,可以制成较为轻薄的构件,也被应用于建筑外墙饰面等。

在现有的部分试验研究中,配筋UHPC受弯构件的力学行为表现出与普通钢筋混凝土结构的一些相似性[8-14],因此可以借鉴普通混凝土结构的部分分析方法。同时,由于UHPC的应用带来的混凝土强度的极大提高,使得高强钢筋强度的充分利用成为可能,即在有限的截面内通过对高性能材料的使用,达到普通混凝土结构难以实现的强度和刚度。

胡利等对6个跨高比为10的钢筋混凝土梁开展了受弯性能试验研究[14],试件包括2根配置HRB600钢筋的UHPC梁,2根配置HRB600钢筋的UHPC-NC(普通混凝土)复合梁以及2根配置HRB400钢筋的C40混凝土梁,考察了上述3种截面形式的梁分别在适筋和超筋状态下的力学行为。基于上述试验[14],将进一步运用有限条带法分析程序对试验结果进行分析,并对试验参数进行扩展研究。通过参数分析,得到了不同配筋率下UHPC梁的力学行为变化规律,并对部分区域配置UHPC的混凝土梁进行了研究,对UHPC组合截面的优化配置提供了建议。

1 有限条带法计算模型

有限条带法基于以下基本假设：1)截面满足平截面,高强钢筋与普通混凝土、超高性能混凝土黏结良好,普通混凝土与超高性能混凝土交界面黏结良好,无相对滑移;2)不考虑剪切变形的影响;3)不考虑混凝土因为收缩、徐变等其他环境因素导致的应力、应变状态。

图1为文献[14]中的钢筋混凝土试验梁截面,表1、表2为材料主要性能汇总。梁承受弯曲荷载时,截面应变、应力分布如图2所示。图2中As,b、As,m、A′s分别为受拉区底层钢筋、受拉区上层钢筋和受压区钢筋的面积;εs,b、εs,m、ε′s分别为受拉区底层钢筋、受拉区上层钢筋和受压区钢筋的应变;εc,i为某层混凝土条带的应变;Fs,b、Fs,m、F′s分别为受拉区底层钢筋、受拉区上层钢筋和受压区钢筋承受的拉(压)力;xi为某层混凝土条带到上顶面的距离;φ为截面曲率;εN为截面中轴处的应变。

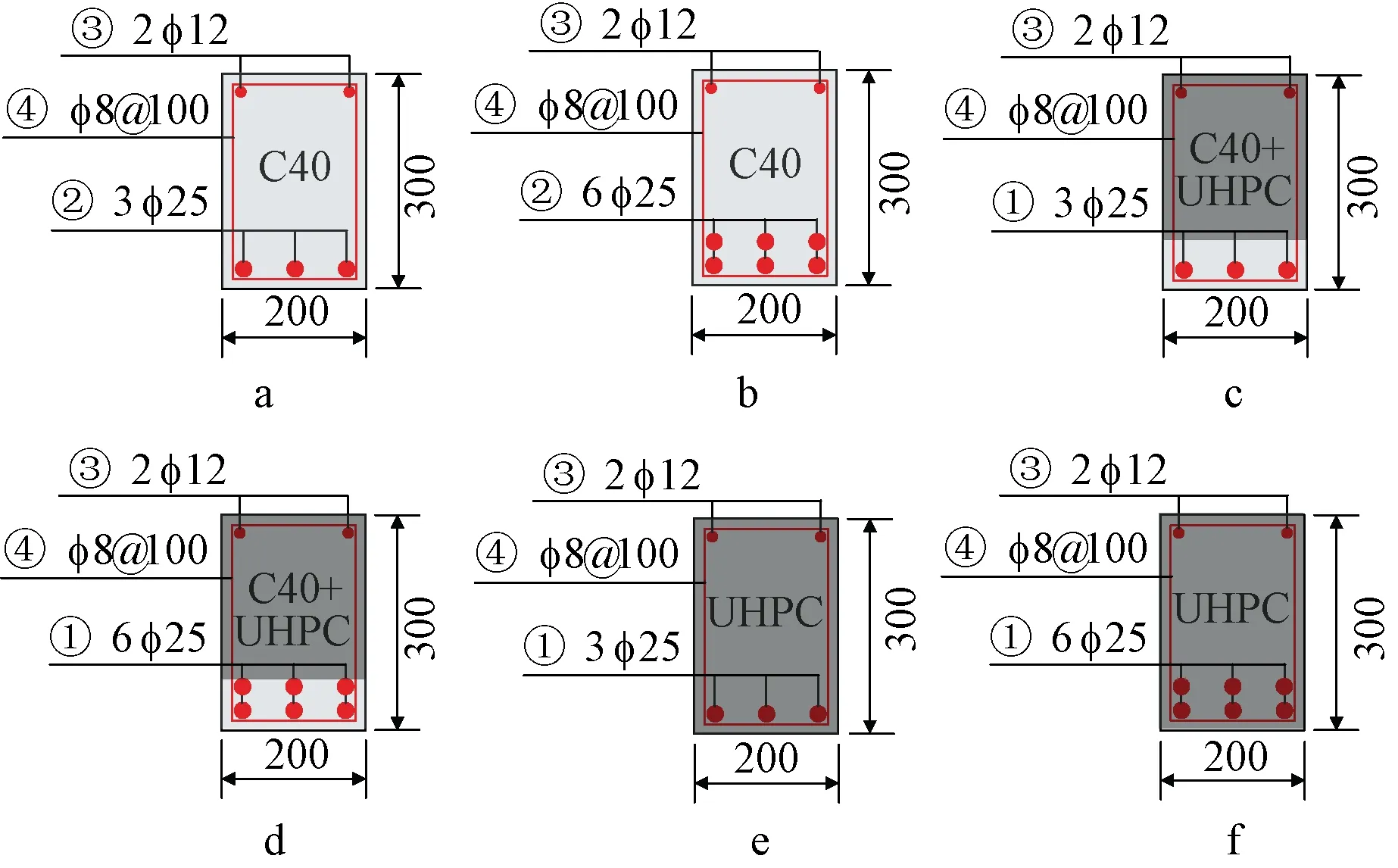
a—L-40-a;b—L-40-b;c—L-UN-a;d—L-UN-b;e—L-UHPC-a;f—L-UHPC-b。图1 试验梁截面[14]Fig.1 Sections of test beam

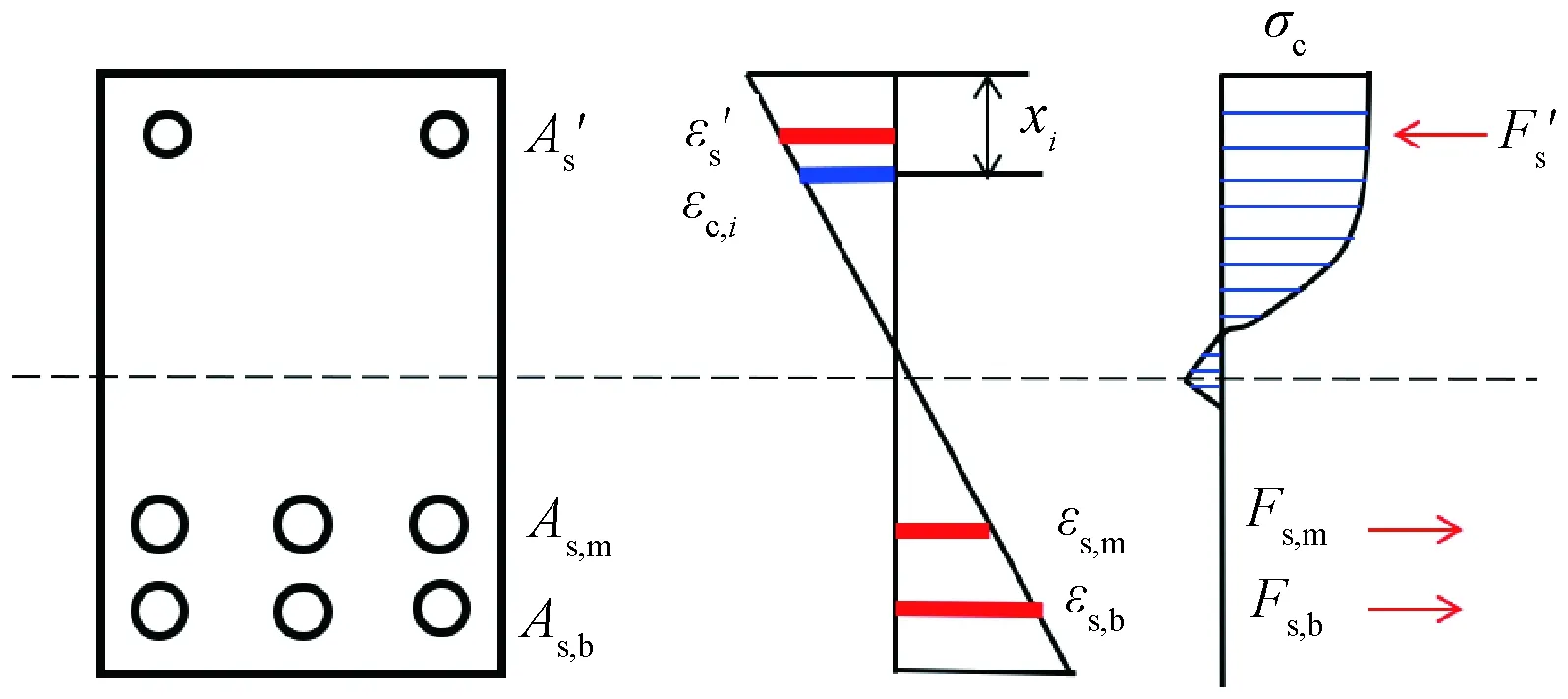
图2 梁截面应力-应变分布Fig.2 Stress-strain distribution diagram of beam section

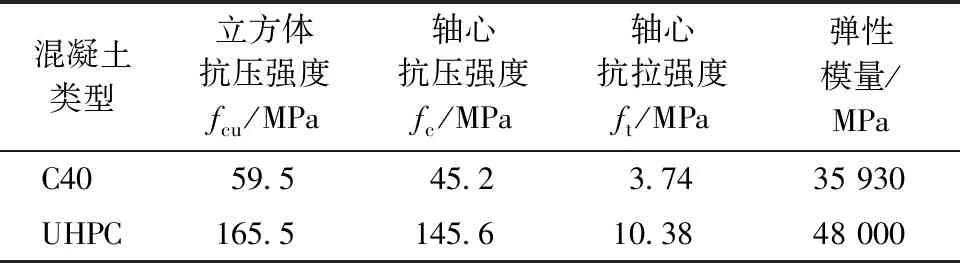
表1 混凝土基本力学性能Table 1 Basic mechanical porperties

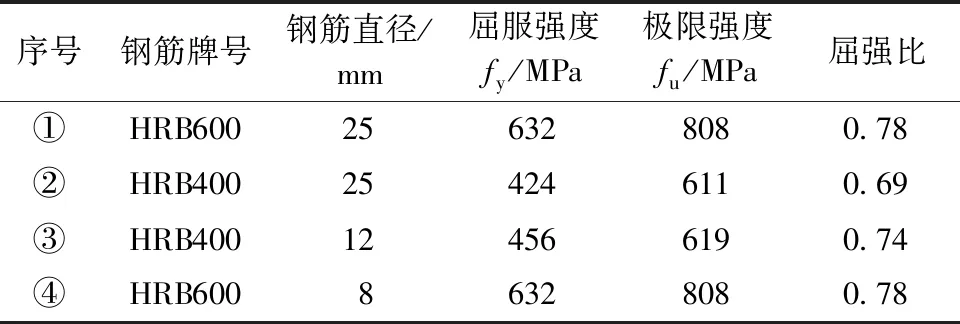
表2 钢筋材性Table 2 Material properties of steel bars

图2中的Fc为混凝土的合力;Mc为混凝土的合力矩(对截面中心取矩),计算方法如下：

(1a)

(1b)

式中：σc,i为某层混凝土条带的应变;b为梁截面的宽度;h为梁截面的高度;n为条带划分数量。

纯弯工况下,应保证钢筋与混凝土轴力的合力为0,此时得到的钢筋混凝土合力矩即对应曲率下梁截面的弯矩,即：

N=Fc+Fs,b+Fs,m+F′s=0

(2)

(3)

有限条带法计算流程如下：

1)指定初始截面曲率为φ;2)假定截面中心点的轴向应变为εN;3)根据平截面假定和几何关系计算出各个条带的轴向应变,包括混凝土条带的εc,i以及钢筋条带的εs,b、εs,m、ε′s等;4)根据各个材料的本构关系,即应力-应变曲线,求出每个条带的应力;5)将每个条带的应力乘以其所代表的面积,得到每个条带的力Fi;6)将各个条带的力求和,判断是否满足轴向平衡条件,若满足,增加φ至下一步,直至达到计算目标值;否则,调整εN直至满足平衡条件为止。

根据以上步骤,可以求得M-φ曲线。相关计算流程详见图3。

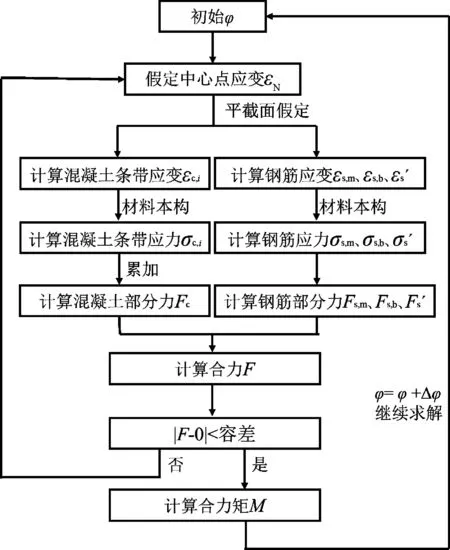
图3 有限条带法计算流程Fig.3 A flow chart for calculations of strip methods

2 材料本构模型

2.1 普通混凝土

普通混凝土单轴应力-应变曲线采用GB 50010—2010《混凝土结构设计规范》[15]建议的无量纲分段模型。其中,单轴受拉应力应变表达式为：

σt=(1-dt)Ecεt

(4)

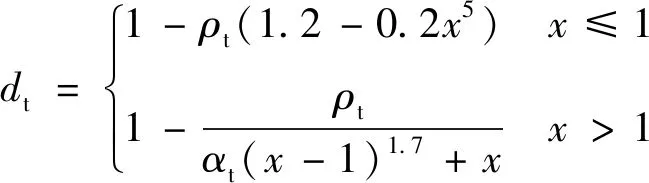
式中：Ec为混凝土弹性模量;dt为混凝土单轴受拉损伤演化参数。

混凝土单轴受压应力应变表达式为：

σc=(1-dc)Ecεc

(5)

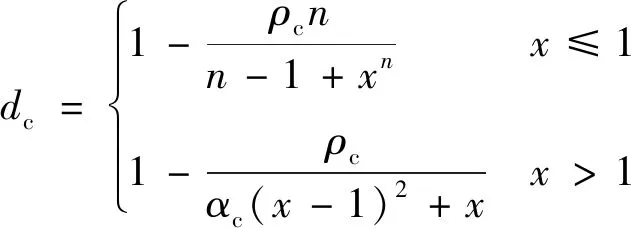
式中：αt和αc分别为混凝土单轴受拉、受压应力应变曲线下降段的参数值;ft,r和fc,r分别为混凝土单轴抗拉、抗压强度代表值;εt,r和εc,r分别为与ft,r、fc,r对应的混凝土峰值拉、压应变;dc为混凝土单轴受压损伤演化参数。各个参数的取值参照GB 50010—2010[15]执行。

表1中立方体抗压强度为试验值,而轴心抗压强度、轴心抗拉强度和弹性模量均按GB 50010—2010推荐的公式计算得到。通过计算得到的混凝土单轴拉、压应力-应变曲线如图4所示。

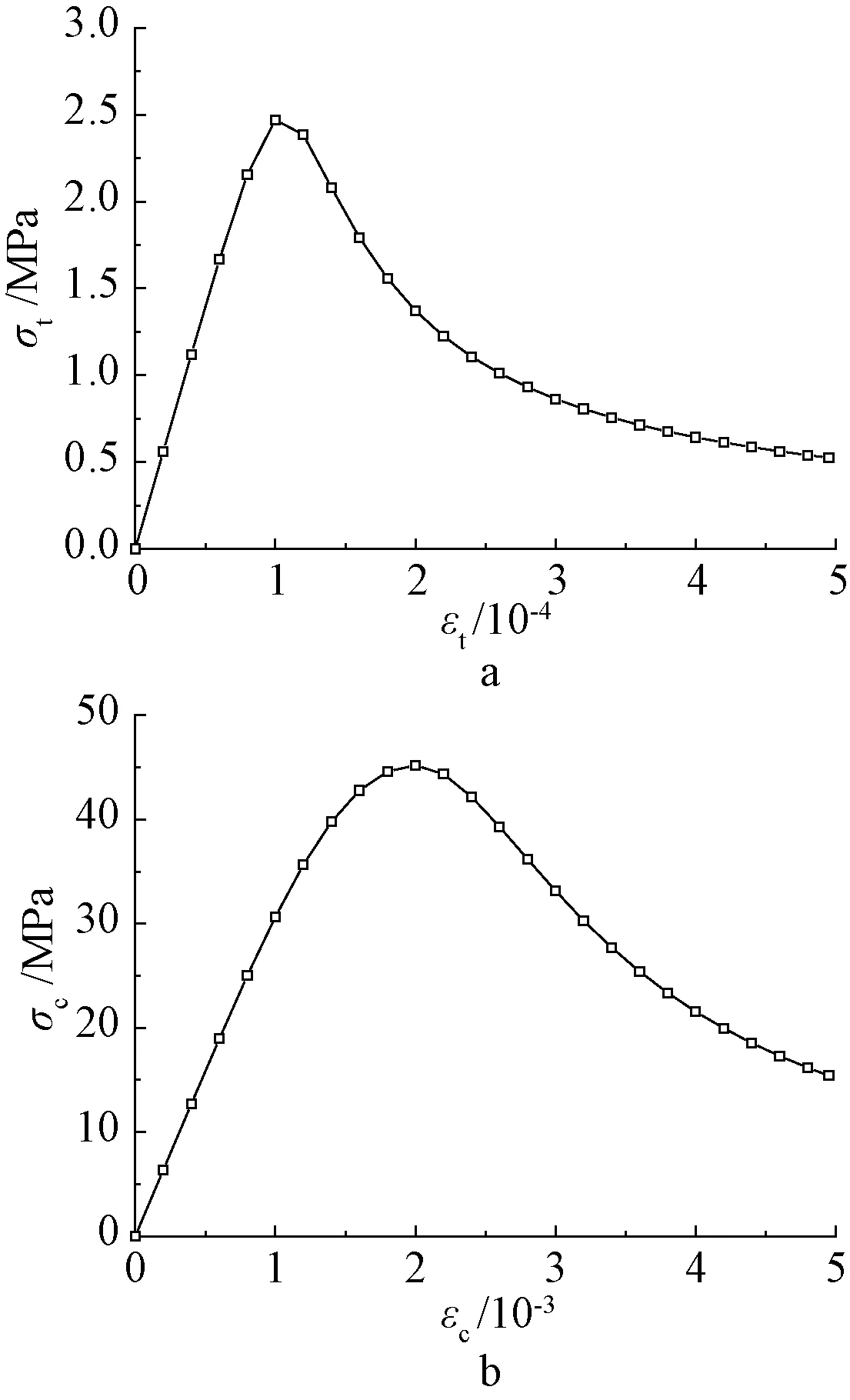
a—单轴受拉曲线;b—单轴受压曲线。图4 C40混凝土单轴应力-应变曲线Fig.4 A uniaxial stress-strain curve for concrete of C40

2.2 超高性能混凝土

超高性能混凝土单轴受压应力-应变曲线采用马亚峰经过试验和数学推导建议的无量纲分段模型[6],其表达式为：

(6a)

(6b)

(6c)

式中：fc和εc,r分别为抗压强度代表值和与之对应的混凝土峰值压应变;A和α为待定参数,按照马亚峰建议的参数取值范围[6],计算取A=1.2,α=8.0。

超高性能混凝土单轴受拉应力-应变曲线采用张哲经过试验提出的具有应变硬化特征的应力应变关系[7],其表达式为：

(7)

式中：fct为低应变硬化阶段的峰值应力;εc,a为UHPC材料单轴受拉应力达到fct时对应的应变,其值取表1中轴心抗拉强度与弹性模量的比值;εc,p为UHPC材料单轴受拉极限应变。

UHPC的材料参数取值详见表1,具体试验方法和结果见文献[14]。其中,立方体抗压强度和轴心抗拉强度为实测值,轴心抗压强度和弹性模量分别按文献[16]和GB 50010—2010[15]计算得到。分析所用UHPC的单轴应力-应变曲线如图5所示。

2.3 钢筋

钢筋单轴受拉曲线采用文献[17]提出的三段模型,其表达式为：

(8)

式中：σ和ε分别为钢筋的应力和应变;Es为钢筋的弹性模量;fy和εy分别为钢筋的屈服强度和屈服应变;k1、k2、k3分别为钢筋硬化起点应变、峰值应变、极限应变与屈服应变的比值;k4为钢筋峰值应力与屈服强度的比值。参考文献[18],计算中取k1=2,k2=10,k3=40,k4取实际强屈比。

钢筋材性如表2所示[14]。考虑到高强钢筋受压时易屈曲导致强度不能充分发挥,故限定钢筋受压应力不大于400 MPa,且采用理想弹塑性模型,即受压屈服之后应力一直维持在400 MPa。

3 结果分析

3.1 计算程序的验证

为验证计算程序的正确性,对文献[14]中的试验结果与数值模拟结果进行对比,对比结果如表3所示。可见：条带法预测值对于适筋的普通混凝土梁(L-40-a)、UHPC梁(L-UHPC-a)及UHPC-NC组合截面梁(L-UN-a)均较为准确,相对误差在±10%以内;对于超筋情况,普通混凝土梁(L-40-b)和UHPC梁(L-UHPC-b)误差稍有增加,相对误差分别为-10.7%和12.9%,亦在合理范围之内,但对于组合截面梁(L-UN-b)的预测值偏差较大,为此,扩大了试验样本数据的验证范围,对文献[9-10]中的UHPC受弯试件承载力也进行了计算。总体来看,条带法计算程序可以较为准确地预测受弯构件的承载力。

3.2 配筋率影响分析

文献[14]针对适筋(配筋率ρ=2.73%)、超筋(配筋率ρ=5.74%)两种情况进行了试验,发现对于UHPC试件,超筋梁的跨中荷载-位移曲线表现出与适筋梁相似的发展规律,具有延性特征。为进一步分析配筋率的影响,选取2%、4%、6%、8%四种配筋率参数对相同几何尺寸的梁进行模拟,得到了普通C40混凝土梁、UHPC梁和UHPC-C40组合梁三种混凝土截面的M-φ曲线,如图6所示。三种截面类型的梁在不同配筋率下的屈服荷载、屈服曲率、峰值荷载、峰值曲率、极限曲率和延性系数见表4。其中,屈服荷载和屈服曲率分别为构件到达屈服点时的荷载及其对应曲率,屈服点根据冯鹏等提出的最远点法[19]确定;峰值荷载和峰值曲率分别为构件到达峰值点时的荷载及其对应曲率;极限曲率为荷载下降到峰值点的85%时的对应曲率;延性系数为极限曲率与屈服曲率的比值。

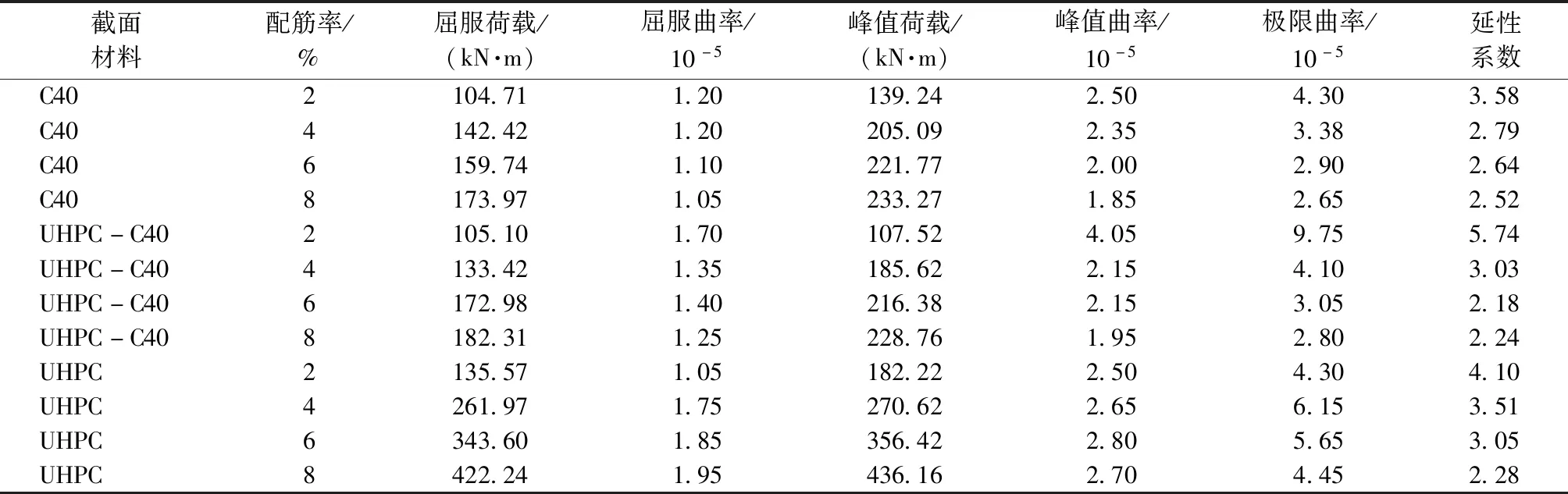
表4 配筋率的影响分析Table 4 Analysis on influence of reinforcement ratios

由图6和表4可知：随着配筋率的提高,各类截面的极限承载力提高,但延性均有所下降。对于纯UHPC截面梁,由于UHPC具有较高的开裂强度以及应变硬化作用,在配筋率很高的情况,仍然表现出较大的延性。因此,不应简单地用普通混凝土结构的配筋率判定UHPC构件是否超筋。上述结果也表明,配筋UHPC受弯构件可以充分利用钢筋的受拉性能,在较小截面的情况下实现较高的承载力和刚度。

3.3 UHPC占比及填充部位的影响分析

在梁底受拉区填充一部分高度的UHPC可起到控制裂缝开展的作用[14],有利于高强钢筋的性能发挥[20]。为研究梁底受拉区不同UHPC占比对构件受力性能的影响,选取试件L-UN-a为研究参考对象,对底部UHPC填充高度分别为10%、25%、40%的C40混凝土适筋梁进行了模拟,梁受力钢筋型号为HRB600,配筋率选用ρ=1%,2%两种配筋率。上述三种截面形式的梁的M-φ曲线如图7所示,表5给出了各梁的屈服荷载、屈服曲率、峰值荷载、峰值曲率、极限曲率和延性系数。

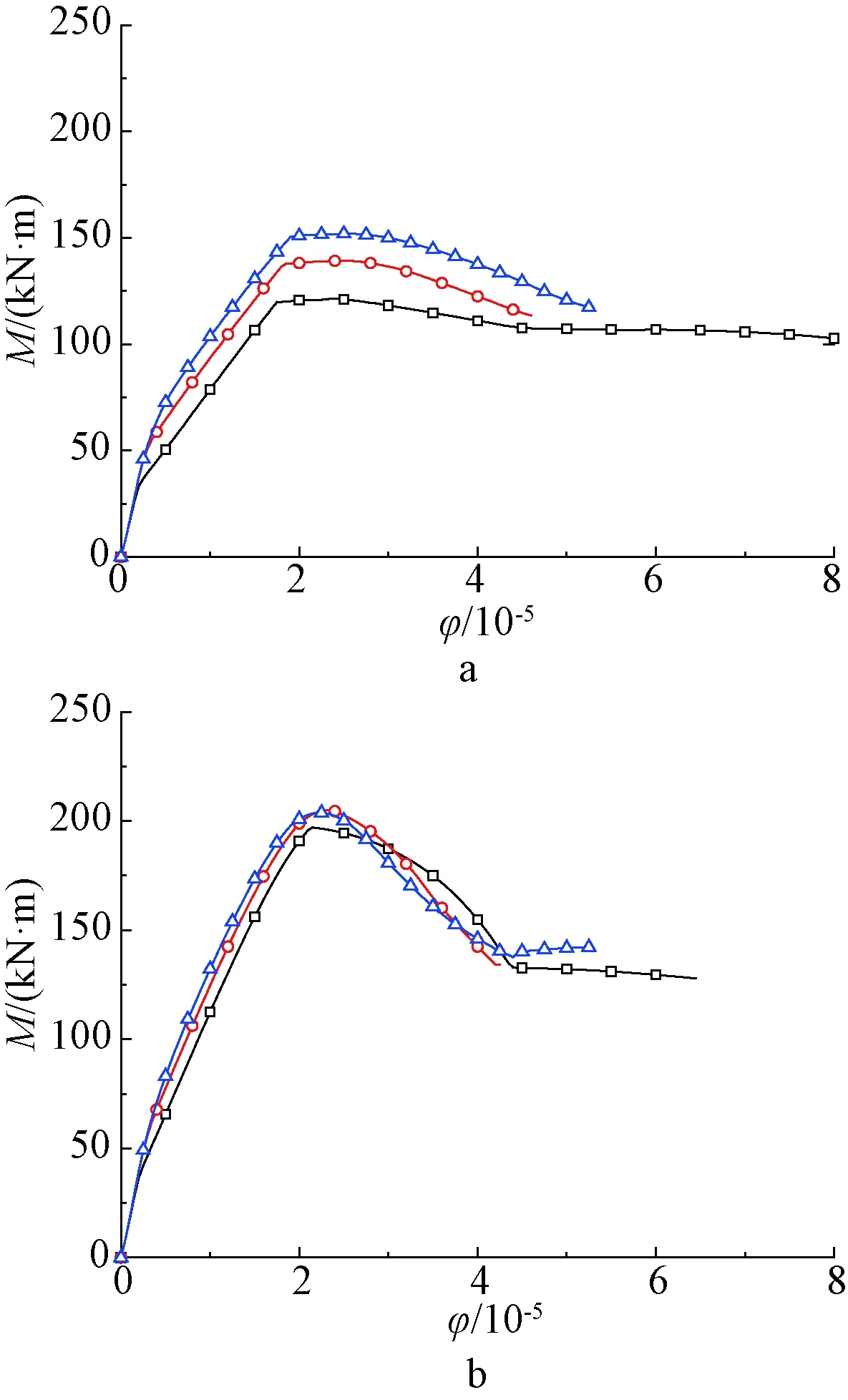
a—配筋率ρ=1%;b—配筋率ρ=2%。—截面底部配置10%UHPC;—截面底部配置25%UHPC;—截面底部配置40%UHPC。图7 底部不同UHPC占比下梁的M-φ曲线Fig.7 M-φ curves of beams with different UHPC ratios at bottoms

表5 在截面底部配置不同高度UHPC的影响Table 5 Effect of different height UHPC at bottoms of sections on mechanical characterisfics

由图7和表5可知：对于梁底部分配置UHPC的UHPC-NC组合截面梁,随着构件截面底部UHPC占比的增加,构件的承载力提高,而峰值曲率差别不大。在UHPC的应变强化作用下,构件在钢筋完全屈服前后会产生一个大于极限弯矩的弯矩峰值,该峰值标志着UHPC的受拉作用已经得到充分的发挥,这种现象在较低配筋率呈现得更明显,即随着梁底UHPC占比的增加,配筋率ρ=1%的构件承载力增幅和极限曲率更大。

实际上,在配筋率较大时,受压区混凝土破坏可能会早于受拉区钢筋屈服,不利于钢筋强度的发挥,尤其是当受力钢筋采用屈服点更高的高强钢筋时。因此,在构件受压区填充UHPC对于提高承载力和高强钢筋强度地发挥有利,这在文献[14]的试验中也有体现。为进一步研究UHPC填充部位的影响,对底部25%配置UHPC,顶部、底部各25%配置UHPC,顶部25%配置UHPC以及全截面配置UHPC四种情况进行了模拟。模型考虑2.73%和5.74%两种配筋率,分别代表普通C40混凝土梁的适筋和超筋状态。上述四种截面形式的梁的M-φ曲线如图8所示,表6给出了各梁的屈服荷载、屈服曲率、峰值荷载、峰值曲率、极限曲率和延性系数。

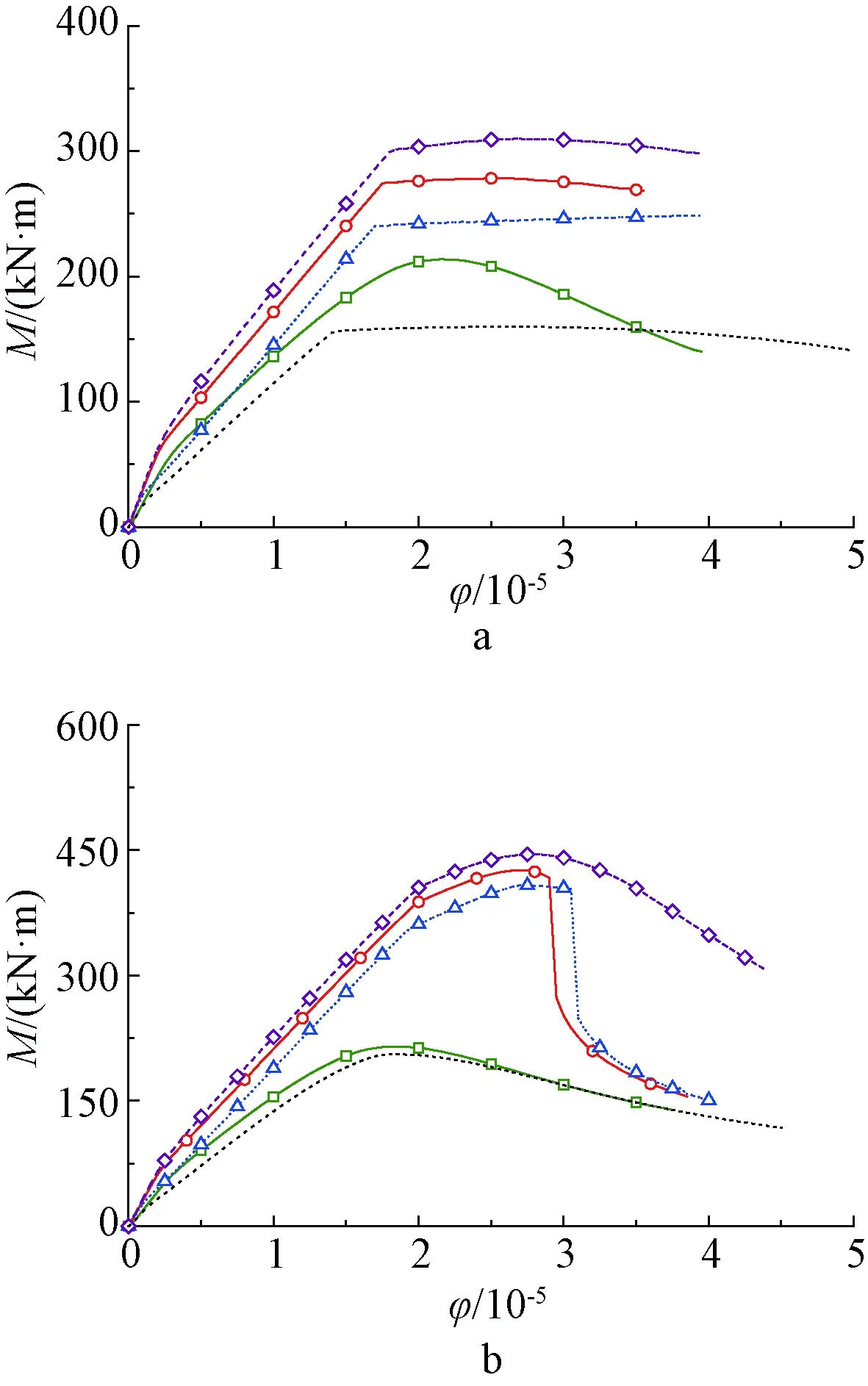
a—配筋率ρ=2.73%;b—配筋率ρ=5.74%。……全C40;—底部25%UHPC;—顶部、底部各25%UHPC;-----顶部25%UHPC;-----全UHPC。图8 不同部位配置UHPC的梁的M-φ曲线Fig.8 M-φ curves of beams with different height at bottoms of sections UHPC

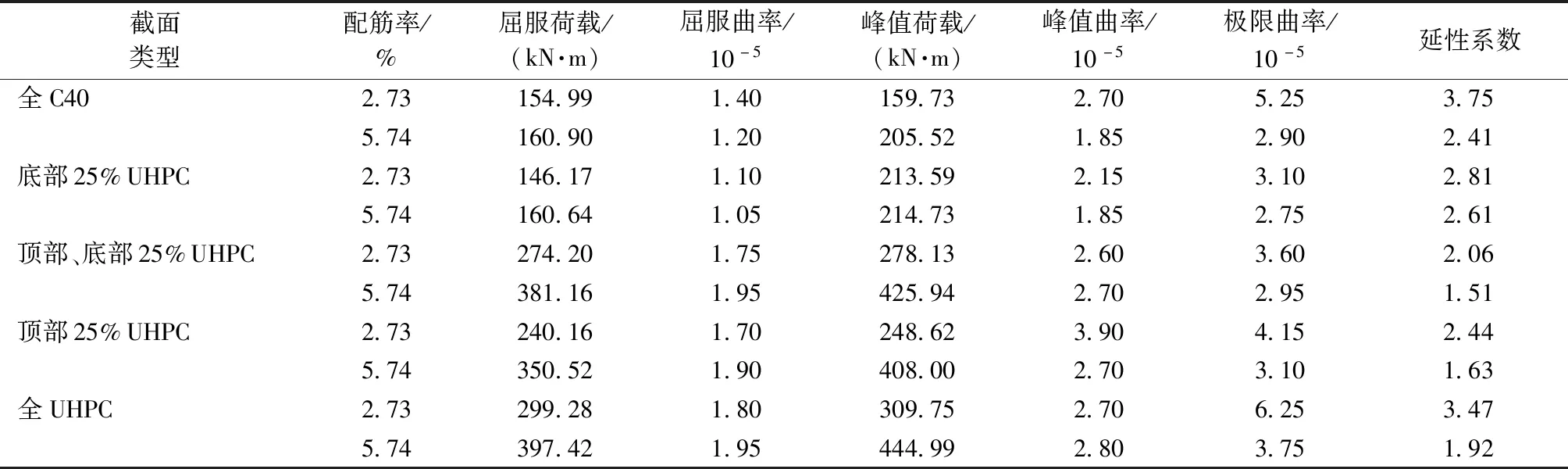
表6 在不同部位配置UHPC对构件性能的影响Table 6 Effects of UHPC configuration in different parts on component performance

由图8、表6可知：对于配筋率适中的构件,采用上述四种形式配置UHPC都能使承载力得到明显提升,且具有较好的延性,承载力提升效果由大到小的排序为全截面配置UHPC顶部、底部各25%配置UHPC顶部25%配置UHPC底部25%配置UHPC,虽然在底部配置UHPC对承载力提升的效果较差,但能更好地抑制开裂,提高极限曲率,综合考虑受力性能和经济性能,推荐在受压区和受拉区各配置部分UHPC;而对处于超筋状态中的梁,由于梁的破坏受混凝土抗压强度控制,底部配置UHPC作用不大,在顶部25%配置UHPC就能取得非常显著的承载力提升效果,但为了保证构件的延性,应尽可能采用全截面配置UHPC的方式,而不宜采用组合截面的形式。