绝对值的化简求值问题的几种类型及解法解析

聂玉成

绝对值在化简求值问题、解方程或不等式问题中都会涉及.解答含绝对值问题的关键就在于去掉绝对值符号.一般遵循的原则是：先判断绝对值符号中式子的正负，再根据法则去掉绝对值符号.单个绝对值的问题一般比较简单，但是有的题目会同时出现多个绝对值或多重绝对值，这样就使题目变得复杂了.下面介绍几类有关绝对值的化简求值问题，供大家参考.

一、含单个绝对值问题

一个题目中只含有一个绝对值是最基础的题目，此时只需考虑去绝对值符号的条件，即对于任意数|a|：（1）当a>0时，|a|=a；（2）当a= 0时|a|=0；（3）当a<0时；|a|=-a.同学们在解题时应根据题设条件或挖掘隐含条件，确定绝对值符号里代数式的正负.若题目对含绝对值代数式的字母没有限制条件，须运用分类讨论的方法来解答.

例1若|x|=3，|y|=2，且|x-y|=y-x，求x+y的值.

分析：此题中| x |=3，可知x =±3；| y |=2可知y =±2 .由题中| x-y |= y-x可知y≥x .由此可以推断，当y = 2时，x可以为±3，此时x+y =-1或5；当y = -2时，x只能为-3，此时x+y =-5.最后综合所有情况即可得解.

解：∵| x |=3，∴x =±3；

同理可得y =±2，

∵| x-y |= y-x，

∴y≥x，

①当y =2时，x =-3，

x+y =-1.

②当y =-2时，x =-3，

则x+y =-5.

综合①②得x+y的值可能是-1、-5.

评注：求解此题是利用| x-y |≥0挖掘了隐含条件y≥x，然后确定x和y的可能值，简化了分类讨论的种类.同学们在求解过程中一定要仔细观察，充分挖掘题目中的隐含条件.

二、含多个绝对值问题

有些含有绝对值的题目中往往不止一个含绝对值的代数式，可能是两个、三个甚至是更多个含绝对值的代数式，通过“+”“-”“×”“÷”等运算符号连接.此时，去绝对值符号就需要先找出每个绝对值的零点值，再把全体实数分段，然后在每一实数段中化去绝对值符号，最后分类讨论去绝对值的结果.

例2化简：| 3x +1|+| 2x-1|.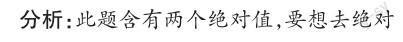

三、含多重绝对值问题

有些较为复杂的问题中含有多重绝对值符号，即绝对值符号中还有绝对值符号，我们称这种形式为多重绝对值.在求解多重绝对值问题时，需要依据“由内而外”的顺序逐一去绝对值符号，逐步减少绝对值的嵌套层数，来解答问题.

例3已知x<-3，化简：|3+|2-|1+ x |||.

分析：这是一个含有多重绝对值符号的问题，在求解时需要根据“由内而外”的原则逐层去绝对值.首先根据x的范围判断出1+x< 0，所以最里层绝对值|1+ x |= -（1+ x）.第二層|2-|1+ x||可以转化为|2-[-（1+ x）]|=|3+ x|因为x<-3，所以3+ x< 0，即|2-|1+ x ||=-（3+ x）.最外层|3+|2-|1+ x |||可转化为|3+[-（3+ x）]|=|- x |.这样根据x的取值范围一步步利用绝对值的代数意义即可化简.

解：①最内层：

∵x<-3，∴1+ x<- 2 < 0，

∴|1+ x |= -（1+ x），

②第二层：

|2-|1+x||=|2-[-（1+x）]|=|2+（1+x）|=|3+x|，

∵x<-3，

∴3+ x< 0，

∴|3+ x|=-（3+ x），

∴|2-|1+ x||=-（3+ x），

③最外层：

|3+|2-|1+ x |||=|3+[ -（3+ x）]|=| -x |，

∵x<-3，∴-x >3>0，

∴| -x |= -x，

∴|3+|2-|1+ x |||= -x，

综合①②③可得|3+|2-|1+ x |||化简后为-x .

评注：此题数值比较简单，但含有多重绝对值符号.在去绝对值符号时要由内而外逐层将3个层次的绝对值符号内部的数或式同“0”作比较，大于等于“0”的直接去绝对值；小于“0”的一定要添加“-”.

绝对值是中学数学中的一个重要概念常与其他知识结合起来考查.同学们只要牢牢掌握去绝对值的基本方法，结合“由内而外”的运算顺序和“分类讨论”的思想方法，解题就会变得非常容易.