基于智能反射面与用户关联的1比特反馈波束赋形算法

袁田浩，杨少石,2*

（1.北京邮电大学信息与通信工程学院，北京 100876；2.泛网无线通信教育部重点实验室，北京 100876）

1 引言

受益于超材料领域的发展，智能反射面(Intelligent Reflecting Surface，IRS)成为6G 预研中的热点空口技术之一[1]。其无源、无射频链路的特点有助于降低系统的成本、复杂度与能耗[2]。对于IRS 辅助的无线通信场景下的波束赋形，除基站原有的主动波束赋形增益以外，IRS的反射单元提供被动波束赋形增益，因此需要对两者进行联合设计[3]。

为充分利用被动波束赋形增益，IRS 的反射单元数量通常很多。如果对接入点(Access Point,AP)到IRS 信道和IRS 到用户设备(User Equipment,UE)的信道状态信息(Channel State Information,CSI)均进行实时更新，所需的信道估计开销难以接受。一部分研究者选择使用随机相移优化的方式进行设计，Tao Q 等人研究单天线发射机通过IRS 向多个单天线用户广播公共消息的场景，IRS 在每个时隙上用一组随机系数进行反射以节省信道估计开销[4]。Nadeem Q 等人通过IRS 的随机旋转方案增加多用户分集效应，不需要与IRS 有关的CSI，但此方案没有利用IRS 的被动波束赋形增益[5]。Psomas C 等人基于随机相位旋转，结合编码与IRS分区选择算法，分析单IRS辅助单UE通信的中断概率与能量效率[6]。值得注意的是，这些研究仅局限于单IRS系统。

同时，由于存在乘积距离路径损耗现象，IRS 的部署位置也会对实际效果产生较大影响。You C 等人研究了单天线用户系统中两个合作的IRS 与传统的单IRS 情况下的速率，指出在考虑IRS 信道存在估计误差以及训练开销的条件下，两个合作分布式IRS 可实现提高速率[7]。Zhang S 等人研究了对称信道条件下的单IRS 与双IRS 辅助下的时分多址与频分多址系统速率，指出该假设下集中式部署性能优于分布式部署[8]。但目前对于多个IRS 分布式部署的研究相对较少。Mei W 等人研究了多基站多IRS的系统，每个IRS 通过无源波束赋形进行相位对齐，协助关联的基站向用户传输，同时随机散射来自其他同信道基站的信号，从而在网络中增加额外的信号和干扰路径[9]。

综上所述，目前分布式IRS 部署方式下的低瞬时CSI 依赖的波束赋形设计方案较少。因此，本文提出分布式IRS 辅助的多AP 服务多UE 场景下的IRS-UE用户关联方案及波束赋形算法。对系统场景进行分析建模，基于大尺度衰落参数设计关联方案以及设计低CSI 依赖的1-bit 反馈算法。仿真结果表明了用户关联方案对用户性能存在显著影响，所提1-bit反馈算法方案不同步长下均能收敛，并有效接近相位对齐波束赋形方案的信干噪比(Signal to Interference plus Noise Ratio,SINR)。

2 系统模型

2.1 系统场景

本文考虑如图1所示的多个分布式IRS辅助的多AP 服务多UE 场景，其中K个配备有L根天线的AP，通过K个装有M个反射单元的IRS，服务K个单天线UE。每个AP 只为其服务的单一UE 发射有效信息，但系统中存在来自其他AP 的同频干扰。AP 与UE 的关联关系已经由UE 接收到的各AP 的参考信号功率强弱决定，每对AP与UE对应编号相同。同时为了减轻信道估计的开销与系统设计成本，每对AP与UE只由一个IRS进行被动波束赋形。

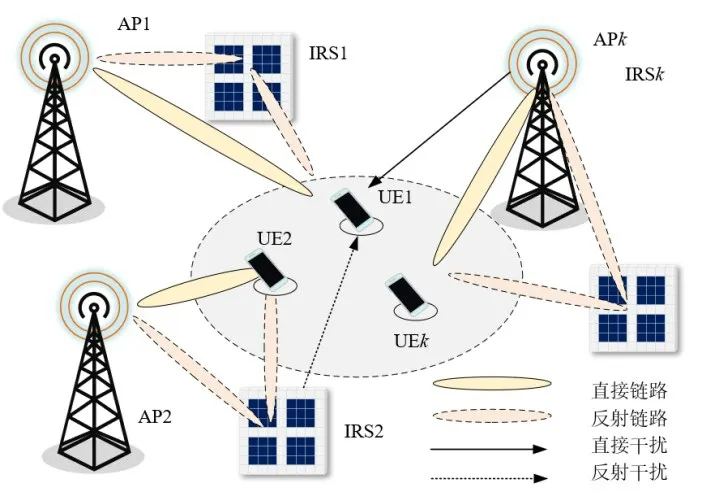
图1 分布式IRS辅助下多AP服务多UE场景

为方便后续表示，定义以下集合表示下标范围，K、J ≜{1,2,…,K}与ℳ ≜{1,2,…,M}分别表示AP-UE 对的编号集合、IRS 的编号集合与IRS 的反射单元编号集合。同时假设每个IRS 的反射单元没有能量损失，反射幅度均为1，第j个IRS 的第m个反射单元的相位可调范围为0 到2π，即θj,m∈[0,2π)。因此，第j个IRS 的反射矩阵可以表示为对角阵Φj=，其中相位前的i表示虚数单位。为便于理论推导，本文使用了理想的IRS 反射条件，对于离散相位取值的影响，将在3.2 节进行讨论。在本文后续的研究中，考虑到乘积路径损耗模型的影响，只考虑经IRS 单次反射的信号，忽略从AP 到UE的经IRS二次及以上的信号。

用fn,k=[fn,k,1,fn,k,2,…,fn,k,L]∈ℂ1×L表示第n个AP到第k个UE 的直接信道，与此同时gj,k=[gj,k,1,gj,k,2,…,gj,k,M]∈ℂ1×M表示第j个IRS 到第k个UE的信道。第n个AP 到第j个IRS 的信道表示为Hn,j=[hn,j,1,hn,j,2,…,hn,j,M]H∈ℂM×L。若该网络为富散射环境，假设所有信道的小尺度衰落均为独立的瑞利衰落，则有，其中n,k∈K,j∈J。其中与分别对应为第n个AP 到第k个UE 的直接信道、第n个AP 到第j个IRS 的信道以及第j个IRS 到第k个UE的信道的大尺度衰落系数。

为便于各AP 间进行分布式处理以及降低波束赋形的复杂度，假设第k个AP 仅根据其对应服务的第k个用户的直接信道进行最大比传输(Maximum Ratio Transmission,MRT)波束赋形，主动波束赋形矩阵为：

为便于后续推导，利用MRT 波束赋形的特性，本文等效考虑K个配备有单根天线的AP，于是第n个AP到第k个UE的等效直接信道为：

第n个AP到第j个IRS的等效信道为：

假设对于第k对AP 与UE，其对应的IRS 编号为j，令AP-IRS-UE 信道与经MRT 波束赋形的AP-UE 信道相位对齐，则有：

2.2 接收信号与干扰

分析第k个UE 接收到的来自第k个AP 的期望接收信号，xk为第k个AP 发往第k个UE 的原始信号，满足，Pk为第k个AP 的发射功率。为便于分析，假设所有AP 的发射功率相同均为P。期望接收信号具体为：

引入二元变量aj,k,j∈J,k∈K，当aj,k=1，表示第j个IRS服务第k个UE；当aj,k=0，表示第j个IRS不服务第k个UE。由于每个IRS只服务一个UE，进而有：

同时，由于已经进行式(5)的相位对齐，有：

接下来考虑第k个UE 受到的其他未与之关联的AP 的同频干扰。这些AP 将各自通过其与第k个UE 的直接链路以及通过所有IRS 反射的反射链路造成干扰，分别对应式(9)右侧的第一项与第二项。可得：

3 基于IRS与UE关联的1比特反馈波束赋形

3.1 基于ASAINR的IRS与UE关联

本小节将对平均信号功率与平均干扰加噪声功率的比值(Average Signal to Average Interference plus Noise Ratio,ASAINR)[9]进行推导与相应理论分析。考虑第k个UE处的平均接收SINR，为：

其中σ2表示接收端的噪声方差。由于式(10)从数学上难以分析，引入ASAINR 作为下界进行近似。通过yk与Ik各自独立的条件，以及Jensen不等式得到：

式(11)不等式右侧的取值仅与大尺度衰落的系数有关。首先考虑E{ |yk|2}，结合式(8)与式(6)，并利用关联IRS的级联信道与非关联IRS的级联信道的独立性，得到以下表达式：

将式(12)表示为E{ |yk|2}=PA+PB，A代表第k对AP 与UE 直接链路及与之关联的IRS 反射链路的同相信号的期望。B为未与之关联的其他IRS随机反射的信号的期望。由于不同IRS 各信道之间相互独立，后续推导假设不与第k个UE关联的各IRS的反射单元系数可视为在[0,2π)均匀分布。

首先考虑表达式A，将其展开为：

将式(4)与式(8)代入，得：

下面分析Qj,k，令qn,j,k=βn,jηj,k,n,k∈K,j∈J 表示第n个AP 经由第j个IRS 到第k个UE 处的平均大尺度信道增益，利用各信道为瑞利衰落的性质，有：

同理，利用非关联的IRS 之间级联信道的独立性以及二元变量aj,k取值只有0和1的特性，可得：

将式(14)(15)(16)(17)代入E{ |yk|2}=PA+PB得：I

经过类似的推导过程，可以得到第k个UE 接收到的平均干扰为：

为使系统中用户的最低ASAINR 最大，得到以下公式：

其中，Λ=[a1,a2,…,aK]∈{0,1}J×K为所有可能的关联情况。以上问题可通过在各大尺度衰落参数均已获得的情况下，对各IRS 与不同用户配对逐次求解。

接下来分析AP 的天线数量L以及IRS 的反射单元数量M对ASAINR 的影响。考虑式(18)，可以观察到第k个UE 的接收期望信号由三项组成，其中第一项主动波束赋形增益随着AP 的天线数量L线性增加，第二项随IRS 的反射单元数量M二次增加，第三项随IRS 的反射单元数量M线性增加。第二项是由于相关IRS 进行被动波束赋形得到的增益，第三项是由于非相关IRS的对有用信号随机散射造成的。

对于第k个UE 受到的干扰，分析式(20)，随着RS 的反射单元数量M正比例增长，这是因为其他未与之关联的AP 发射的信号，均会经过所有的IRS 进行随机的反射。所以若一个UE 没有与IRS 相关联，其无法得到相应的随M二次增加的被动波束赋形增益，还会受到所有的IRS 进行随机反射的干扰。而且当M的值较小时，随M二次增加的被动波束赋形增益未必能弥补所有的IRS进行随机反射的干扰。

3.2 基于1-bit反馈的主被动联合波束赋形

本小节将基于1-bit 反馈的主被动联合波束赋形算法推广到基于ASAINR 确定IRS-UE 关联的多AP服务多UE 的场景中。3.1 节中推导的ASAINR 基于式(5)进行的严格相位对齐，这对信道估计的精度有极高要求，估计误差无法避免。本小节基于1-bit反馈的主被动联合波束赋形对相位对齐方案进行逼近，主要思路是：通过UE根据其接收到的信号强度变化，每次进行开销为1bit的反馈。AP通过接收到的反馈指示，对IRS 的各反射单元的相移进行一定范围内的随机相位改变。通过不断重复上述过程，IRS 的各反射单元的相移逐渐收敛至使经过被动波束赋形的信号与主动波束赋形信号同相的效果。

假设已经通过3.1 节所提算法，基于ASAINR 确定相应的AP-IRS-UE 关联。下面对多IRS 辅助的多对AP-UE 系统下基于1-bit 反馈的主被动联合波束赋形进行说明。

首先在进行1-bit 反馈相关流程之前，已基于ASAINR 确定相应的AP-IRS-UE 关联，各AP 利用其对应UE 的直接信道进行MRT 波束赋形，第k个UE处的接收期望信号如式(6)所示。假设在持续时间为T个时间单位的信道相干期内，各信道的参数保持不变。

在t=1 的时刻，各AP 对与之关联的IRS 的各反射单元相位进行随机初始化，即：

其中θt,k,i表示在时刻t，第k个IRS 的第i个反射单元的相移系数。同时各UE初始化接收信号功率r0,k=r1,k，假设各UE 可以通过码分等方式获取参考信号的接收强度。

在t≥2的时刻，每个IRS的所有反射单元相位进行随机变化，具体表示为：

其中δt,k,i在[-Δ,Δ]均匀分布，Δ为每次随机相移变化的最大步长，其范围为(0,π]。为便于表示，假设所有IRS 随机相移变化的最大步长均相同。实际场景中反射单元的相位取值范围是离散的，不妨设离散相位间隔为δ，1-bit 反馈算法的随机相移变化的最大步长为nδ，那么1-bit 反馈算法的相位变化范围为从-nδ到nδ，其中n为正整数。相位离散取值的间隔越小，1-bit 反馈算法收敛后的效果越接近主被动波束赋形相位对齐的效果。为观察1-bit反馈算法的理论性能，后续仿真仍采用连续相位取值。

在时刻t，第k个UE 处的接收信号功率为rt,k。若rt,k>r0,k，第k个UE 反馈指示“1”，并令r0,k=rt,k；若rt,k≤r0,k，第k个UE 反馈指示“0”，并保持r0,k不变。对于第k个AP，若收到反馈指示为“1”，则令θ0,k,i=θt,k,i,i=1,2,…,M；若收到反馈指示为“0”，则保持θ0,k,i,i=1,2,…,M不变。引入二元变量bt,k，当UE 反馈指示“1”时，bt,k=1，反之bt,k=0。对于时刻t≥2，IRS的各反射单元相位可以表示为：

在时刻t，第k个UE处的接收信号为：

进而，可以计算出时刻t第k个UE 的SINR 与对应的速率。算法流程如表1 所示。所提算法不断更新反射单元相位与最高接收信号功率值，直至达到一定运行次数。在1-bit 反馈算法的执行过程中，也可采用设置固定SINR 门限的方式，在SINR 达到预设门限时停止迭代，进而节省1 比特反馈算法的开销。

表1 多IRS辅助的多对AP-UE系统下1-bit反馈

4 仿真结果分析

为验证3.1 节中对于IRS 反射单元数量M对所关联用户ASAINR的影响，考虑2个单天线AP、2个单天线UE、1 个具有M个反射单元的IRS 组成的系统，其中AP1 服务UE1，AP2 服务UE2，并设置如下参数：P1=P2=40dBm，σ2=1，。考虑以下两个场景：场景1 中设置；场景2 中设置。分别考虑UE1 是否得到IRS 服务的两种情景，进行仿真。需要注意，以上参数设置仅为验证M对所关联用户ASAINR的影响。

图2 展示了场景1 与场景2 中UE1 是否得到IRS服务的共四种情景下的反射单元数量M与UE1 的ASAINR关系，横坐标为IRS的反射单元数量M，纵坐标表示UE1 的ASAINR。首先分析UE1 没有IRS 辅助的情景，在场景1 中，将相关参数代入式(21)得，随着M的增大，γ1将趋于的比值2。

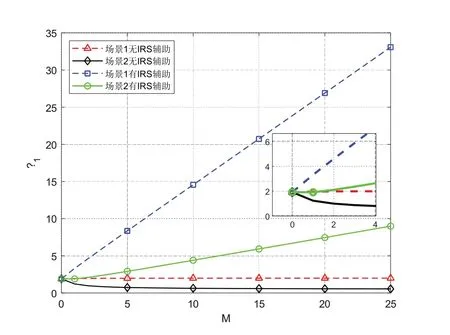
图2 反射单元数量M与UE1的ASAINR关系图

下面关注场景2，将相关参数代入式(21)得，随着M的增大，γ1将趋于的比值0.5。可以看出，没有IRS辅助时，随着反射单元数量的增加，γ1趋于受大尺度衰落系数影响的定值。接着分析UE1有IRS辅助的情景，在场景1与场景2中UE1的ASAINR，在M较大时，均随着M的增加而增大，这是因为被动波束赋形产生与M2成正比例的增益，同时只引入与M成正比例的干扰。场景1与场景2中γ1随着M增加的速率受大尺度衰落系数影响。同时注意到，在M较小时，被动波束赋形产生的增益未必能抵消干扰，如场景2中IRS辅助的情景，γ1在初始阶段产生下降。由此可见，若要充分利用被动波束赋形增益，需要反射单元数量高于一定值。

接着考虑K=4个发射功率为40dBm的AP，每个AP 配置单天线，通过K个装有M个反射单元的IRS，服务K个单天线用户的场景。建立笛卡尔坐标系，AP1 的坐标为(-25,3)，AP2 的坐标为(25,2)，AP3 的坐标为(25,-2)，AP4 的坐标为(-25,-3)，IRS1 的坐标为(-3,5)，IRS2 的坐标为(4,5)，IRS3 的坐标为(4,-4)，IRS4 的坐标为(-3,-4)，UE1 的坐标为(0,3)，UE2 的坐标为(2,0)，UE3 的坐标为(0,-1)，UE4 的坐标为(0,-2)。以上IRS的序号由3.1节提出的算法确定，其他参数设置如表1所示，仿真场景的俯视图如图3所示。

图3 多AP-IRS-UE系统仿真场景俯视图

表2 中的大尺度衰落由3GPP 标准[10]中的城区宏小区(Urban Macro，UMa)场景给出，所有信道的小尺度衰落均为瑞利衰落。利用蒙特卡洛方法，取2000次不同的信道实现,将各IRS 的反射单元数量从0 逐渐增加至1000。

表2 多AP-IRS-UE系统部分仿真参数设置

图4 比较了各个UE 的ASAINR 与IRS 反射单元数量的关系。UE1 距离为其服务的AP 与IRS 较近，受到来自其他UE的较强干扰，但在M增加时，其获得的波束赋形增益可以有效弥补来自其他UE的干扰增强。UE2距离为其服务的AP最近，在M较小时，主动波束赋形的增益使其ASAINR 最高，但在M增加时，受大尺度衰落系数影响，其获得的被动波束赋形增益相较于UE1 较弱，性能提升弱于UE1。UE3 由于距离为其服务的AP 与IRS 均较远，所以其主被动波束赋形增益相较于其他UE 较低，在M较小时，ASAINR 增长缓慢，在M增加时，获得的被动波束赋形增益也弱于UE1 与UE2。UE4 由于距离为其服务的AP 与IRS也较远，在M较小时，其主被动波束赋形增益相较于UE1、UE2较低，ASAINR增长缓慢，在M增加时，由于距离与其关联的IRS 更近，获得的被动波束赋形增益高于UE2。从以上结果可以看出，要实现较高的IRS被动波束赋形增益，需要提升反射单元数量。同时UE 与为其服务的AP 及IRS 的距离也会影响其性能，为使距离AP更远的UE有更好的使用体验，应为其配备具有更多反射单元的IRS或增加IRS数量。

图4 各UE的ASAINR与IRS反射单元数量关系

图5 展示了M为50 时，步长取值下分别为π/30、π/20、π/10 的1-bit 反馈算法的收敛情况与对应信道状态下使用D-MRT、E-MRT 算法的收敛速率。场景为单IRS 辅助的单AP 服务单UE 系统，AP 到UE 信道、AP 到IRS 信道、IRS 到UE 信道的大尺度衰落均值均设为0.1，小尺度衰落均服从瑞利分布。将根据AP 到UE 直接链路信道CSI 求得的MRT 波束赋形记作DMRT，将如式(5)调整IRS反射单元相位使之与直接链路信号相位对齐的联合波束赋形记作E-MRT。需要注意，对于不同的步长取值，在经过足够多次反馈以后，均能达到收敛，但各自的收敛速度不同。为了便于观察，图中只画出了横坐标为100 的整数倍时对应的结果。D-MRT 只利用AP 主动波束赋形的增益，忽略IRS 的被动波束赋形作用，IRS 对信号进行随机反射，该算法对应的接收信号强度从整体来看最弱。EMRT 实现了IRS 被动波束赋形后的信号与主动波束赋形对齐，其对应的接收信号强度最强，但相位对齐意味着需要掌握AP到IRS信道与IRS到UE信道的精确CSI，随着M的增大，对应的信道估计开销也随之增大。步长取值下分别为π/30、π/20、π/10的1-bit反馈算法均能达到收敛，但步长越小的算法收敛趋向的值越接近E-MRT 的效果，说明步长越小的算法收敛之后更接近直接链路与反射链路相位对齐的状态，相较于E-MRT 性能损失也越小。需要说明，1-bit 反馈算法并不需要对与IRS 信道有关的CSI 信息，这在M增大时具有节省信道估计开销的作用。然而，由于步长小的情况其每次相位波动范围较小，收敛速度相对变慢。因此应结合收敛时与E-MRT 的性能差距与收敛速度综合决定步长取值。

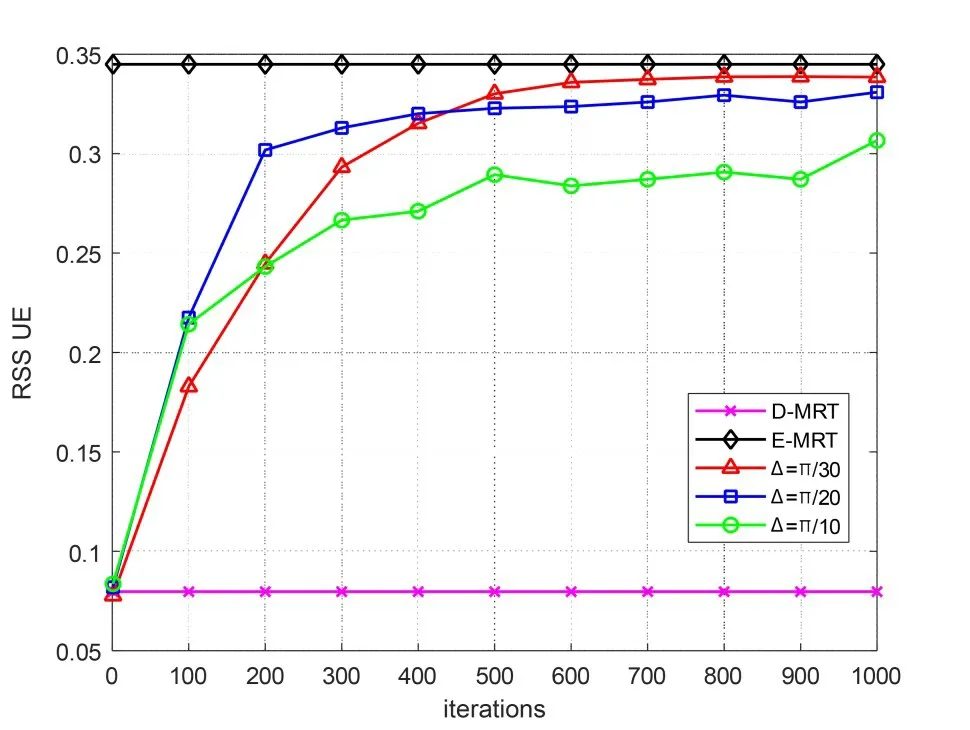
图5 不同步长取值下的1-bit反馈算法的收敛速率

图6 比较了多AP-IRS-UE 系统将所有UE 对应的步长均设为π/30，M为50时，每次反馈以后的各UE接收信号强度，可以看出，各UE的接收信号强度在进行1-bit 反馈以后，从整体来看，呈现出上升直至收敛的趋势，收敛后的接收信号强度与随机反射时（初始值）相比有明显的提升。各UE在几乎相同的迭代次数处接近收敛，这是因为各UE的步长取值相同，且与之相关联的IRS 反射单元数量也相同。同时注意到，各UE 的接收信号强度短期内存在波动，并非持续上升，这是因为随机调整相位时可能导致效果变差。

图6 多AP-IRS-UE系统中的1-bit反馈算法的收敛速率

对于基于ASAINR的多AP-IRS-UE系统1-bit反馈算法，将所有UE对应的步长均设为π/30，运行至收敛，同时考虑D-MRT、E-MRT以及根据直接链路与随机反射时的反射链路的综合信道MRT算法，对UE1的平均SINR进行仿真，得到图7。M的取值范围为[10,100]，每次取值利用蒙特卡洛方法，取2000次不同的信道实现。

图7 不同波束赋形算法下UE1的SINR

由图7可得，E-MRT算法下的UE1的SINR最高，收敛后的1-bit反馈算法与E-MRT算法性能相差约0.5dB，需要指出，1-bit反馈算法达到收敛需要一定次数迭代，但可以通过估计IRS相关的信道减少迭代次数，这种信道估计性能需求低于进行严格相位对齐的E-MRT算法。对于D-MRT与综合信道MRT，IRS的被动波束赋形增益并没有得到充分利用，导致即使反射单元数量增加，两种算法对应的SINR也没有明显改变。之所以E-MRT算法对应的SINR随反射单元数量增加而增长速度较慢，是因为在图7的仿真系统设置中，反射单元数量的增加还没有显著高于带来的干扰，这与图4的结果一致。

5 结论

本文针对分布式多AP-IRS-UE 系统中的IRS 关联与波束赋形设计问题，提出一种基于统计CSI 的IRS 关联方案与低瞬时CSI需求的波束赋形算法。首先利用大尺度衰落参数推导ASAINR，通过ASAINR确定IRS 与用户关联。然后在确定IRS 关联的基础上，提出无需精确瞬时CSI 的基于1-bit 反馈的IRS 反射单元相位调整方案。仿真结果显示UE 受到IRS 辅助与没有IRS 辅助下的ASAINR 存在显著差异，以及大尺度衰落参数对IRS 关联UE 的影响需要提升反射单元数量弥补。通过适当选择相位调整的步长提升1-bit反馈算法的收敛速率，收敛后的1-bit反馈算法能够接近主被动波束赋形相位对齐时的性能，同时降低对信道估计精度的要求。