基于试验设计的乘用车前纵梁结构耐撞性优化分析
2023-06-12姜玉秀莫秋云韩勇庞毅李志扬
姜玉秀 莫秋云 韩勇 庞毅 李志扬
(1.桂林电子科技大学,桂林 541004;2.厦门理工学院,福建省客车先进设计与制造重点实验室,厦门 361024;3.广西数仿科技有限公司,柳州 545000;4.马来西亚博特拉大学,吉隆坡 858700,马来西亚)
1 前言
中国新车评价规程(New Car Assessment Program,C-NCAP)中的乘员保护测试试验有4 项,其中正面100%重叠刚性壁障碰撞试验是检验车辆结构耐撞性能的重要项目[1]。在汽车正面碰撞工况下,整车吸能结构(前纵梁、前防撞梁)的承载能力对整车的安全性能具有重大影响。
国内外已在前纵梁的材料失效、轻量化设计和结构优化方面进行了大量研究:在前纵梁失效方面,赵世婧[2]、陈光[3]、王振[4]、易有福[5]等针对材料属性、压溃吸能等方面开展研究,对影响前纵梁承载的弯曲失效因素进行分析,基于分析结果对某前纵梁进行了优化设计并试验验证;Duan 等[6]从轻量化设计角度提出了一种新型变厚-变截面(Variable Rolled Blank-Variable Cross-Sectional,VRB-VCS)结构,分析结果表明,VRB-VCS 柔性薄板的耐撞性相较于均匀厚度柔性薄板明显提高,且质量明显减轻;Wang等[7]以前纵梁为优化对象,通过静态拓扑优化得到了轴向最大刚度,通过动态拓扑优化得到了满足轴向强度要求的最大吸能结构,并采用非支配排序遗传算法-Ⅱ(Non-dominated Sorting Genetic Algorithms-Ⅱ,NSGA-Ⅱ),通过提高比吸能、降低最大压溃力来提高前纵梁的耐撞性。现有研究大多仅针对前纵梁的材料、结构进行研究,对前纵梁横截面分析相对较少[8]。除对前纵梁的相关研究,刘云刚等[9]也对前防撞梁的材料、结构等进行优化分析,杨国勇等[10]对乘用车前端的车体规划进行了分析,综合对比,前纵梁对整车的吸能影响更重要。本文在探讨前纵梁内外板材料厚度的同时,将前纵梁横截面积作为研究对象之一,探讨其对前纵梁结构耐撞性的影响。
2 前纵梁有限元模型搭建
前纵梁是正面100%重叠刚性壁障碰撞工况的主要吸能部件,前纵梁的结构设计是否合理,直接决定了整车的结构耐撞性。研究表明,汽车发生正面碰撞时,前纵梁的传力率超过75%,吸能率超过34.5%[11]。图1 所示为仿真得到的关键零部件能量吸收与力传递的比例,左、右侧前纵梁吸能比远高于其他零件。汽车前纵梁的主要失效形式是折弯失效和压溃失效。正面碰撞时,压溃失效是较为理想的失效形式,可以有效地吸收碰撞过程中产生的能量。但由于临界角等因素的存在,汽车前纵梁往往会发生折弯失效,极大地削弱整车的结构耐撞性。
汽车碰撞试验是非线性试验项目,包含汽车各零部件的接触、材料、结构等大量非线性元素,试验过程涉及各零部件的瞬态大范围变形与瞬时大距离位移,研究过程十分复杂[12]。目前汽车碰撞安全领域主要采用的仿真分析方法是有限元分析法[13]。本文利用ANSA 建立某插电式混合动力轿车的前纵梁有限元模型,如图2 所示。纵梁横截面尺寸为218.3 mm×113.3 mm。本文使用3 mm、5 mm和8 mm的尺寸对前纵梁进行网格划分,经对比发现,5 mm的网格可以较好地模拟实际情况且计算时间适中。

图2 前纵梁模型
前纵梁各组成部件的材料和厚度信息如表1所示。前纵梁内、外板的密度为7.85×103kg/m3,弹性模量为205 MPa,材料特性曲线如图3 所示。内板与外板采用焊接连接,前纵梁盖板与连接板采用螺栓连接。网格划分完成,各零部件连接为一个整体,对前纵梁设置自接触,自接触关键字设置为*CONTACT_AUTOMATIC_SINGLE_SURFACE_ID。

表1 零件材料与厚度
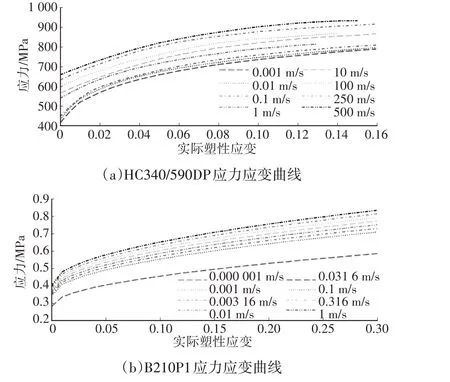
图3 不同冲击速度条件下的材料属性
3 前纵梁结构耐撞性分析
前纵梁落锤试验可以有效模拟前纵梁在整车正面100%重叠刚性壁障碰撞过程中的受力和吸能情况,相对于整车碰撞,落锤试验所用的计算时间短,优化分析相对简单,所以本文采用前纵梁的落锤试验进行仿真分析。
3.1 落锤试验仿真模型建立
前纵梁模型搭建完成后,利用ANSA 软件搭建落锤的有限元仿真模型。选取质量为210 kg的椭圆形重锤轴向撞击前纵梁,撞击速度为50 km/h,为保证落锤试验的稳定性,选取前纵梁盖板处前350 mm区域作为试验区域,删去350 mm 之后的区域,并将前纵梁盖板前330~350 mm 范围完全约束,确保整个前纵梁在受到完全撞击的过程中不发生非必要的运动,产生多余的能量。前纵梁与落锤的有限元模型分别准备完成后,建立前纵梁与落锤的接触模型,接触的关键字设置为*CONTACT_TIED_SHELL_EDGE_TO_SURFACE_ID,速度的关键字设置为*INITIAL_VELOCITY。落锤试验示意如图4所示。

图4 落锤试验示意
模型准备完毕后,利用LS-DYNA 程序进行有限元仿真计算。时间步长是LS-DYNA 每一步积分运算所消耗的时间,决定了计算的稳定性,若时间步长超过临界值,则计算不稳定,时间步长临界值A为:
式中,ε为系统阻尼比;ωmax为系统最大固有频率。板壳单元的计算时长公式为:
式中,Ls为单元的特征长度;ρ为质量密度;E为弹性模量。
材料为20号钢的网格(密度为7.85×103kg/m3,泊松比为0.3,弹性模量为205 MPa,单元长度为5 mm)的计算时间步长约为9.78×10-7ms,因整个碰撞模型中各零部件的密度和弹性模量不完全相同,为适应整个模型,落锤试验的时间步长取为7×10-7ms。落锤试验在45 ms 内可完成并有少部分回弹,故取45 ms 的计算时长可得到完整的碰撞过程,每1 ms 生成一帧图像。采用的高斯单点积分法会导致仿真计算中产生一部分沙漏能,沙漏能若不超过总内能的5%,可认为计算有效,图5 所示为沙漏能曲线和内能曲线,沙漏能未超过总能量的5%,计算有效。
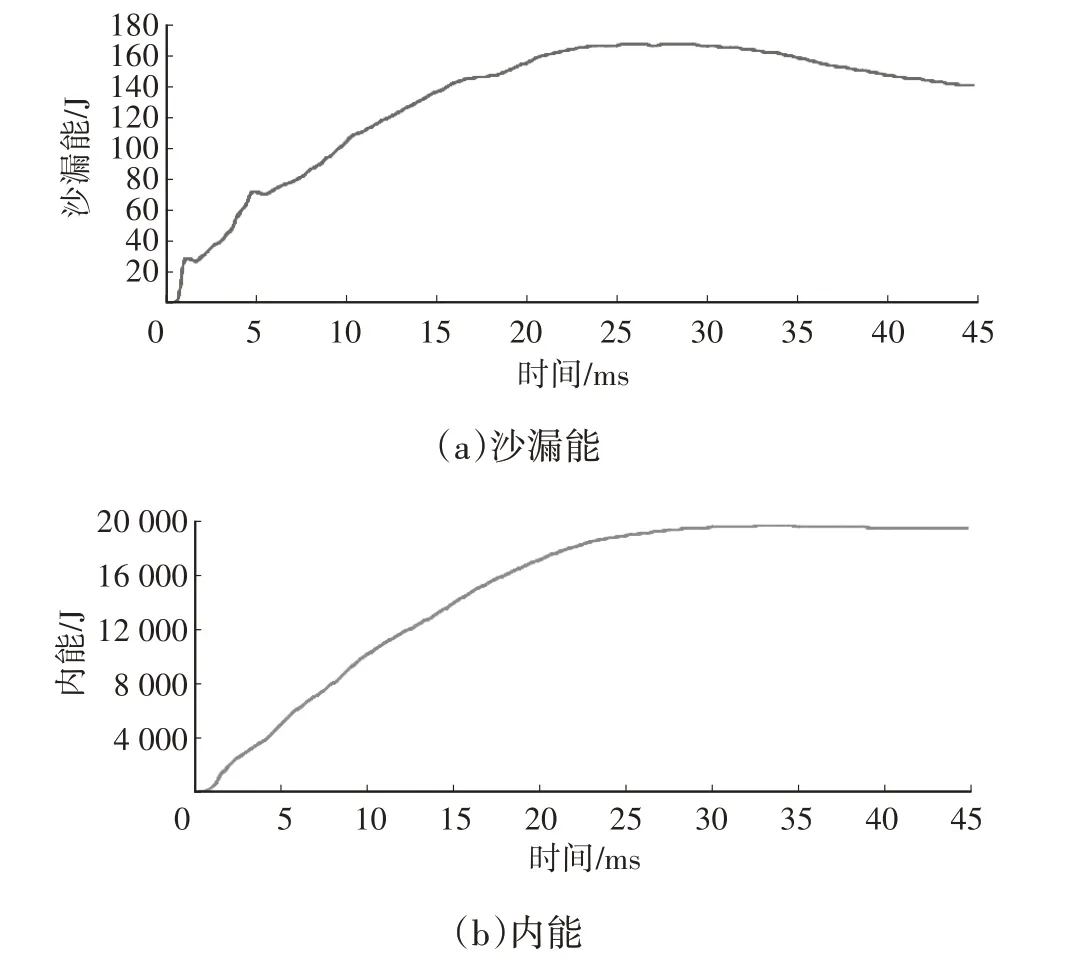
图5 能量曲线
3.2 仿真分析结果
为了评估前纵梁的结构耐撞性,采用比吸能SEA、平均压溃力MCF和压溃效率Q作为评价指标,SEA、MCF和Q越大,则能量吸收效率越高,前纵梁的变形越理想,结构耐撞性越好。
SEA、MCF和Q的数学表达式分别为:
式中,EA为碰撞过程中前纵梁吸收的能量;M为前纵梁质量;D为前纵梁变形量;F为最大峰值力。
LS-DYNA 计算结果如图6、图7 所示,SEA=7 859.16 J/kg,MCF=101.61 kN,Q=25.25%。由图7 可以看出,前纵梁变形不完全,前纵梁后端几乎未变形吸能。

图6 落锤试验结果曲线

图7 落锤试验结果
4 响应面优化
基于上述落锤试验所用的前纵梁模型进行优化,主要以前纵梁截面积和内外板材料、厚度为优化目标。如图8 所示,基础模型的前纵梁横截面的尺寸为218.3 mm×113.3 mm,在该模型的基础上网格变形,将长、宽分别增加、减少6 mm 进行分析优化,得到3 种不同截面尺寸的前纵梁,并对3 种前纵梁进行响应面优化(Response Surface Methodology,RSM)[14]。
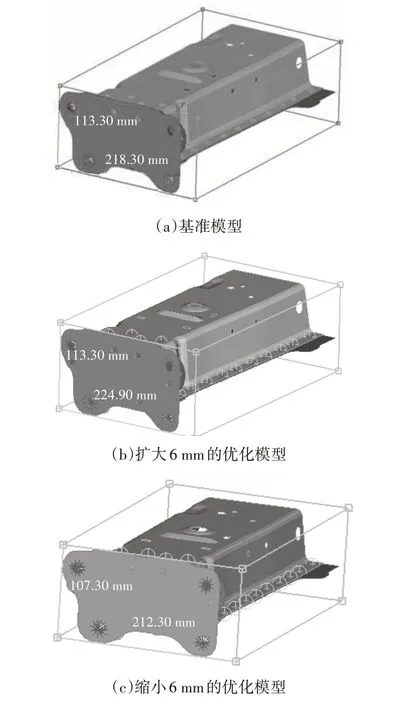
图8 3种前纵梁模型
4.1 试验设计
在进行响应面优化前,首先利用试验设计(Design of Experiment,DOE)选取样本点。本文以内、外板的材料与厚度作为设计变量,内、外板材料选取B280VK、B400/780DP、HC340/590DP、HC420/780DP、HC550/980DP、B210P1 6 种材料,外板厚度选取为1.0 mm、1.2 mm、1.3 mm、1.4 mm、1.5 mm、1.6 mm、1.7 mm、1.8 mm、2.0 mm、2.2 mm,内板厚度选取为1.0 mm、1.2 mm、1.4 mm、1.6 mm、1.8 mm、2.0 mm、2.2 mm、2.4 mm,利用哈默斯雷采样法,选取60 个采样点作为响应面拟合的输入数据。哈默斯雷采样法是一种空间填充的采样方法,在响应面为高度非线性的情况下,相比于拉丁超立方采样法,哈默斯雷法在空间上的采样更加均匀,可以更好地填充整个空间[15]。
4.2 响应面拟合
采样完成后,得到60 个采样点数据,将其带入原模型中进行分析运算,得到相应的输出响应值。根据输入响应与输出响应的关系,得到拟合多项式。常用的拟合方法是最小二乘法,一阶线性最小二乘法拟合的数学表达式为:
式中,F(x)为优化目标;a0为多项式常数项;a1、a2为多项式系数;x1、x2为设计变量;e为误差。
在使用最小二乘法进行拟合时,如果拟合精度R²<0.8,则拟合精度过低,可以利用调整多项式的阶次的方法提升拟合精度,R²的数学表达式为:
式中,SSE为和方差;SST为原始数据与均值之间差的平方和。
当拟合多项式的阶次大于4 阶时,拟合精度随着多项式阶次的提升不会有明显变化。本文中SEA的拟合精度为0.96,MCF的拟合精度为0.94,Q的拟合精度为0.92,均大于0.9,拟合精度足够,则拟合公式可用。
最小二乘法拟合的加权系数固定不变,拟合效果不理想。本文采用优化的最小二乘法拟合,根据采样点到取值点距离的函数,定义DOE 各采样点处非固定值加权系数,形成最小二乘法的近似拟合公式。由于优化的最小二乘法的加权系数是随设计变量变化的函数,所以优化的最小二乘法最终无法形成确定的拟合解析式。
4.3 响应面优化
得到响应面拟合公式后,模型验算可以直接利用公式所得规律进行,大幅提升运算效率。选取300 个样本点进行验算,利用全局响应面优化法进行模型优化,寻找满足目标值的最优解。响应面优化是一种多目标优化算法,无法得到确切的最优解值,而是根据多目标响应要求,得到满足要求的最优解集。在3 种不同截面尺寸的模型下,选取截面尺寸为113.3 mm×218.3 mm 的截面,在该截面对应的响应面优化最优解集中可以综合考虑各响应值,得到最优解。图9 所示为各响应值对应的响应面。本文选取前纵梁内、外板厚度分别为1.5 mm 和1.8 mm、材料分别为B420/780DP和HC340/590DP 作为优化结果,优化后SEA、MCF和Q有明显提升,结果如表3 所示。优化后的落锤试验结果如图10 所示。

表3 优化结果
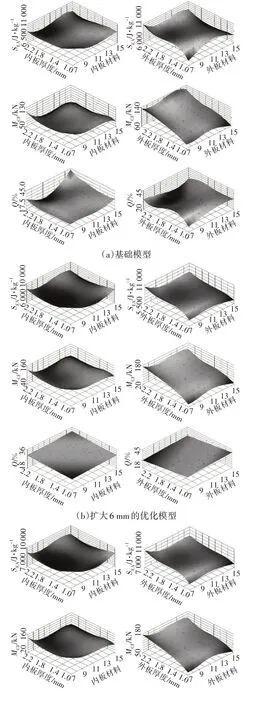
图9 3种前纵梁模型的响应面结果

图10 优化后的落锤试验结果
5 结束语
本文针对某插电式混合动力轿车,搭建前纵梁落锤试验模型并进行有限元仿真计算,通过能量守恒验证了仿真模型的准确性。通过分析计算结果得到最大比吸能、平均压溃力和压溃效率分别为7 859.16 J/kg、101.61 kN 和25.25%,发现落锤下降后前纵梁变形不完全,前纵梁后端几乎未变形吸能。
基于落锤试验所用的前纵梁模型,以其横截面积和内外板材料、厚度为设计变量,以比吸能、平均压溃力和压溃效率为优化目标,使用哈默斯雷采样法和基于改进的最小二乘法的响应面法进行多目标优化。结果表明,优化后汽车前纵梁的最大比吸能提升了1 129.14 J/kg,平均压溃力提升了8.2 kN,压溃效率提升了2.59 百分点,前纵梁变形更加充分,提高了汽车的结构耐撞性。
