基于 SVM 机器学习技术的企业智能化审计建模优化

2023-06-12蔡玲嘉

粘接 2023年5期

蔡玲嘉

摘要：机器学习是人工智能的核心，将其应用于企业审计中，提升企业审计智能化水平。研究从用户、内部业务流程、学习和成长、财务4个角度构建了审计智能化评价指标，并采用经典机器学习算法支持向量机建立企业智能化审计评价模型。为提升支持向量机模型性能，采用回溯搜索优化算法对支持向量机核函数进行优化，将构建的模型与GA-SVM、PSO-SVM 进行对比。结果表明：BSA-SVM 模型的分类识别准确率最高为94.5%，同时迭代时间最短为36.28 s。

关键词：支持向量机；回溯搜索优化算法；智能化审计；技术；建模

中图分类号：TP391.9文献标志码：A文章编号：1001-5922（2023）05-0139-04

Optimizationof enterprisesintelligentauditmodeling basedonSVMmachinelearningtechnology

CAI Lingjia

（Audit Center of Guangdong Power Grid Co.，LTD.，Guangzhou 510060，China）

Abstract：Machine learning is the core of artificial intelligence，and it can be applied to the audit of enterprises to improve the level of enterprise audit intelligence. In this paper，intelligent audit evaluation indicators were con? structed from four perspectives：users，internal business processes，learning and growth，and finance，perspec? tives of users，internal business processes，learning and growth，and finance，then classical machine learning algo? rithm was used to support vector machines to establish an intelligent audit evaluation model for power enterprises. In order to improve the performance of the support vector machine model，a backtracking search optimization algo? rithm was used to optimize the kernel function of the support vector machine，and the constructed model was com? pared with GA-SVM and PSO-SVM.Results showed that the classification recognition accuracy of the BSA-SVM model is the highest 94.5%， and the shortest iteration time is 36.28.

Keywords：support vector machine；backtracking search optimization algorithm；intelligent audit

通过加强审计来严肃财经法纪，反映企业资产、负债、盈亏真实情况，为企业下一步的决策提供精准的数据参考。机器学习技术的快速发展使得企业审计智能化成为大势所趋，而部分企业审计智能化水平比较低，在激烈的企业竞争中处于不利的地位。有机硅材料、橡胶等在电力行业中应用十分广泛，同时审计水平不高，会使得企业的经营决策不科学，增加企业的经营风险[2]。为充分发挥企业审计的作用，必须持续提升企业审计的智能化水平。有报道，采用粒子群算对卷积神经网络进行改进，提出了改进卷积神经网络的故障诊断算法，并将其应用于化工故障诊断中，其平均故障检出率高达91.2%[3]。引入机器学习算法构建了一种海上蒸发波导特性智能化预测的模型，该模型的实际偏差小，相对误差小，在提高我国区域范围内预测蒸发波导高度准确率方面具有良好性能[4]。支持向量机（SVM）作为经典机器学习算法，其性能受到参数的影响比较大，获取SVM 最佳参数是关键，也引起了学术界广泛关注[5]。本研究采用回溯搜索優化算法（BSA）对 SVM 参数优化，得到 BSA-SVM 模型，并将其应用于企业智能化审计中，期待对提升审计工作效率和质量提供参考。

1 企业审计智能化构建

审计工作在企业管理中发挥着至关重要的作用，审计工作的智能化水平直接影响到审计工作开展的效率和质量，进而影响到企业的发展。科学制定企业审计智能化评价指标直接影响到审计工作质量的提升，通过提升企业审计的智能化水平来达到降低企业审计成本的目的。采用平衡计分卡方法构建企业审计智能化水平评价指标，具体如图1所示。

2 基于SVM机器学习的审计智能化模型

2.1 SVM 算法

SVM 是经典的机器学习算法，其按照监督学习的方式对数据分类，属于二元广义分类器。目前，SVM 在文本分类、绩效考核、人脸识别等领域得到了广泛的应用[6-7]。SVM 算法数学性能优良，实际工程应用效果好，引起了学术界的广泛关注。SVM 算法对样本分类的过程是确定分类超平面的过程，其目标是寻找最优超平面；二维状态下的最优超平面如图2所示。

不妨设企业审计智能化水平评价指标与评价结果构成数据集合 D ，即

式中：xi 为审计智能化水平评价指标所构成的向量；yi e {<1 ， 1}为审计智能化水平评价结果。不妨设最优分类超平面方程为[8]：

式中：x 为最优分类超平面法向量；b 为偏置位移。

SVM 算法的核心问题是求解 x 和 b ，使得样本D 满足[9]： {

由于并非所有的样本均能够被正确分割，通过引入惩罚系数和松弛变量的方式来求解。在引入松弛变量之后，少部分的样本点可以在边界线上，同时当样本数据被错误划分或者具有比较多的样本点在边界线上时实施惩罚，这样来确保边距的最大化要求，惩罚系数的大小直接反映了惩罚的强度。在引入惩罚系数 C 和松弛变量ε之后，求解 x 和 b 可以转化为最小值求解问题，即[10]：

为了便于求解，引入拉格朗日乘子 ai ，其拉格朗日函数为：

最小值求解问题转化为对偶问题，即：

对线性不可分割的样本数据，引入核函数将线性不可分割样本升维，达到在高维空间样本线性可分的目的。径向基核函数是常用的核函数，其表达式为[11]：

引入核函数后，决策函数为[12]：

很明显，核函数参数（g）以及惩罚系数（C）对 SVM 的性能具有至关重要的影响，要通过优化算法对参数组合（C ，g）进行优化，从而提高SVM 的分类性能。

2.2BSA 算法

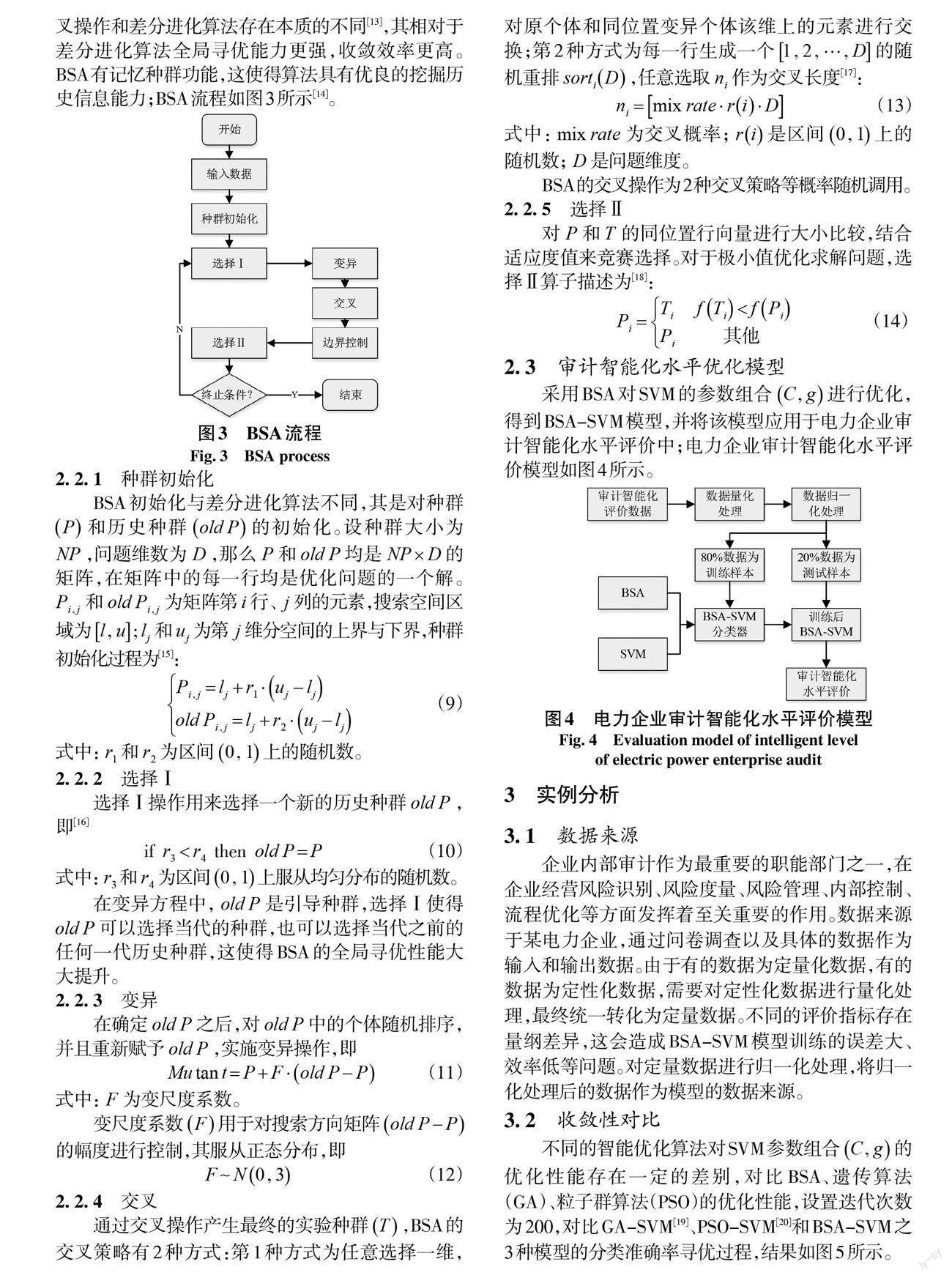
BSA 是Civicioglu P 提出的种群元启发式优化算法，算法的框架和差分进化算法类似；但是变异、交叉操作和差分进化算法存在本质的不同[13]，其相对于差分进化算法全局寻优能力更强，收敛效率更高。 BSA有记忆种群功能，这使得算法具有优良的挖掘历史信息能力；BSA流程如图3所示[14]。

2.2.1 种群初始化

BSA 初始化与差分进化算法不同，其是对种群（P）和历史种群（oldP）的初始化。设种群大小为 NP ，问题维数为 D ，那么 P 和oldP均是NPx D 的矩阵，在矩阵中的每一行均是优化问题的一个解。

Pi.j和oldPi.j为矩阵第i行、j 列的元素，搜索空间区域为[l . u]; lj和uj为第j 维分空间的上界与下界，种群初始化过程为[15]：

式中：r1和 r2为区间（0.1）上的随机数。

2.2.2 选择Ⅰ

选择Ⅰ操作用来选择一个新的历史种群oldP，即[16]

式中：r3和r4为区间（0.1）上服从均匀分布的随机数。

在变异方程中，oldP是引导种群，选择Ⅰ使得oldP可以选择当代的种群，也可以选择当代之前的任何一代历史种群，这使得BSA 的全局寻优性能大大提升。

2.2.3 变异

在确定oldP之后，对oldP中的个体随机排序，并且重新赋予oldP，实施变异操作，即

式中：F 为变尺度系数。

变尺度系数（F）用于对搜索方向矩阵（oldP一 P）的幅度进行控制，其服从正态分布，即

2.2.4 交叉

通过交叉操作产生最终的实验种群（T），BSA 的交叉策略有2种方式：第1种方式为任意选择一维，对原个体和同位置变异个体该维上的元素进行交换；第2种方式为每一行生成一个[1.2.….D]的随机重排sorti（D），任意选取ni作为交叉长度[17]：

式中：mix rate 为交叉概率；r（i）是区间（0.1）上的随机数；D 是问题维度。

BSA的交叉操作为2种交叉策略等概率随机调用。

2.2.5 选择Ⅱ

对 P 和 T 的同位置行向量进行大小比较，结合适应度值來竞赛选择。对于极小值优化求解问题，选择Ⅱ算子描述为[18]：

2.3 审计智能化水平优化模型

采用BSA 对SVM 的参数组合（C .g）进行优化，得到BSA-SVM 模型，并将该模型应用于电力企业审计智能化水平评价中；电力企业审计智能化水平评价模型如图4所示。

3 实例分析

3.1 数据来源

企业内部审计作为最重要的职能部门之一，在企业经营风险识别、风险度量、风险管理、内部控制、流程优化等方面发挥着至关重要的作用。数据来源于某电力企业，通过问卷调查以及具体的数据作为输入和输出数据。由于有的数据为定量化数据，有的数据为定性化数据，需要对定性化数据进行量化处理，最终统一转化为定量数据。不同的评价指标存在量纲差异，这会造成BSA-SVM 模型训练的误差大、效率低等问题。对定量数据进行归一化处理，将归一化处理后的数据作为模型的数据来源。

3.2 收敛性对比

不同的智能优化算法对SVM 参数组合（C .g）的优化性能存在一定的差别，对比 BSA、遗传算法（GA）、粒子群算法（PSO）的优化性能，设置迭代次数为200，对比GA-SVM[19]、PSO-SVM[20]和BSA-SVM 之3种模型的分类准确率寻优过程，结果如图5所示。

从图5可以看出，BSA对SVM的优化效果明显优于GA 和PSO，在经过4次迭代之后就获得了最优值。与BSA 相比，GA 优化SVM 所得到的GA-SVM 模型的分类准确率比较低，陷入了局部最优状态。PSO 相对于GA 的收敛速度比较快，但是PSO-SVM 更加容易陷入局部最优的状态。由此可见，采用BSA 优化SVM 参数组合（C .g）具有收敛速度快、准确性高的优点。

3.3 优化结果对比

分别采用 GA、PSO、BSA 对 SVM 的参数组合（C .g）进行优化，并将优化得到的参数作为SVM的最优参数。采用训练数据分别对GA-SVM、PSO-SVM、 BSA-SVM 进行训练，并采用测试数据对训练好的模型进行测试，优化和测试结果对比如表1所示。

由表1可知，BSA-SVM 對企业审计智能化水平评价的识别准确率为94.5%，明显高于 GA-SVM、 PSO-SVM，识别准确率分别提高了4.3%和8.2%。从迭代的时间来看，BSA-SVM 模型的时间也最短，为36.28 s，比GA-SVM模型缩短了33.58 s，比PSO-SVM 模型缩短了20.5 s。通过对比3种模型的识别准确率和迭代时间，BSA-SVM 模型对企业审计智能化水平的评价具有十分明显的优势。

采用BSA-SVM 模型对企业审计智能化水平进行评价，实际和预测结果对比如图6所示。

4 结语

从4个维度构建了审计智能化水平评价指标，并采用BSA 对SVM 参数优化，提出了基于BSA-SVM 的企业审计智能化水平评价模型。通过与 GA-SVM、 PSO-SVM模型的对比，BSA-SVM对电力企业审计智能化水平评价的识别准确率为94.5%，明显高于 GA-SVM、PSO-SVM，识别准确率分别提高了4.3%和8.2%。BSA-SVM 模型的迭代时间也最短，为36.28 s，比GA-SVM 模型缩短了33.58，比PSO-SVM 模型缩短了20.5 s。结果表明，所提出的BSA-SVM 审计智能化水平评价模型，明显优于其他模型。

【参考文献】

[1] 万婵.电力企业数据资产监控体系的建立[J].粘接，2020，42（6）：73-77.

[2] 张侃，张浩海，顾新桥，等.基于A-Workflow的电力仓储化资产盘活方法研究[J].粘接，2021，46（5）：164-168.

[3] 许洪光，李凤英，郭茜.机器学习算法改进及在化工故障诊断中的应用[J].粘接，2022，49（5）：85-89.

[4] 石广亮，杨铖，王健.基于机器学习的海上蒸发波导特性智能化预测[J].指挥与控制学报，2022，8（2）：198-205.

[5] 张蜀红.基于支持向量机的机械设备故障诊断研究[J].粘接，2021，47（9）：129-132.

[6] 徐竟泽，吴作宏，徐岩，等.融合PCA、LDA 和SVM 算法的人脸识别[J].计算机工程与应用，2019，55（18）：34-37.

[7] 朱亚军，次曲，拥措.基于SVM 算法的藏文微博情感分析研究[J].计算机仿真，2022，39（8）：226-229.

[8] 裴爱根，张洋，黄涛，等.基于支持向量机激光技术提取电力线信息的研究[J].粘接，2022，49（12）：155-159.

[9] 王涛，李治军. PSO-SVM 模型在黑龙江省水资源承载力评价中的应用[J].水电能源科学，2023，41（1）：30-33.

[10] 王昱琛，杨仕教，郭钦鹏，等.基于MPA-SVM的煤矿抛掷爆破爆堆形态预测[J].爆破器材，2023，52（1）：58-64.

[11] 丁茜，赵晓东，吴鑫俊，等.基于RBF 核的多分类SVM 滑塌易发性评价模型[J].中国安全科学学报，2022，32（3）：194-200.