不同温度下榆木方材横截面横纹形变规律研究

钱呈 平海阳 程俊博 齐长啸 孙美岐 者彩兰 蔡英春 赵景尧

摘 要：为探究榆木方材干燥过程中横纹形变规律，以50 mm厚榆木方材为对象，采用数字图像相关技术（Digital Image Correlation，DIC）实时在线监测不同温度下其横截面横纹全场应变分布；分析不同温度下其弦径向应变规律及差异，并探究含水率分布、应变规律以及开裂间联系。结果表明，3种温度下，榆木方材横截面横纹应变分布呈中间小边缘大的趋势；40 ℃下弦、径向最大应变为0.036 6、0.033 6，60 ℃为0.045 2、0.042 3，80 ℃为0.059 8、0.051 1；随含水率下降，弦、径向应变逐渐增大，分别在含水率约30%（60 ℃）、40%（80 ℃）时出现交叉，应变方向出现转变；含水率分布不均导致应变分布差异，开裂出现在应变差异最大时刻后，分别在含水率约15%、30%时出现开裂，温度对榆木方材水分及应变分布影响显著（P＜0.05）。

关键词：数字图像相关技术；应变；温度；方材；木材干燥

中图分类号：S781.71 文献标识码：A 文章编号：1006-8023（2023）03-0116-09

Abstract：In order to investigate the transverse grain deformation of elm square timber during drying， Digital Image Correlation technology（DIC） was used to monitor the full-field strain distribution of the transverse grain at different temperatures in real time and with 50 mm thick elm square timer as the object. The law and difference of radial strain at different temperatures were analyzed， and the relationship between water content distribution， strain law and cracking was explored. The results showed that the transverse strain distribution of elm square timber was small in the middle and large in the edge at three different temperatures. The maximum chord and radial strains at 40 ℃ were 0.036 6 and 0.033 6. At 60 ℃， 0.045 2 and 0.042 3; at 80 ℃，those were 0.059 8 and 0.051 1. With the decrease of water content， the chord strain and radial strain gradually increased， and crossover occured when the water content was about 30% （60 ℃） and 40% （80 ℃）， respectively， and the strain direction changed. The uneven distribution of water content led to the difference of strain distribution. The cracking occurred after the moment of maximum strain difference， and the cracking occurred when the water content was about 15% and 30%， respectively. Temperature had significant effects on moisture and strain distribution of elm square timber （P<0.05）.

Keywords：Digital image related technologies; strain; temperature; square timber; wood drying

基金項目：国家自然科学基金项目（32271786）；国家级大学生创新训练项目（202210225147）

第一作者简介：钱呈，硕士研究生。研究方向为木材干燥。E-mail： 870723458@qq.com

*通信作者：赵景尧，博士，副教授。研究方向为木材物理及干燥。E-mail： zjy_20180328@nefu.edu.cn

0 引言

随着木材行业发展，方材的应用越来越广，广泛应用于家具制造、土建工程等方面。榆木方材更在建筑物横梁、家具主干支撑等方面应用前景广阔[1-5]，其具备材性坚韧、强度硬度适中和抗弯性强等优点，但因其构造不均、干缩系数大，干燥中易产生较大应力，出现变形开裂等缺陷，严重影响木材的利用[6-8]。因此，掌握其干燥过程中应变分布及其变化规律，对干燥工艺的优化与提高干燥质量具有重要意义。

目前，对榆木方材弦径向应变分布及规律研究较少，且切片法、叉齿法等传统干燥应变检测手段会损坏木材结构与完整性，无法检测未切试片干燥阶段应变情况，数据获取存在局限性。数字图像相关技术（Digital image correlation，DIC）是一种无损非接触的高精度光学检测，这一新型全场应变检测技术可用于应变规律的研究，通过获取并分析变形过程中的图像差异获得准确全场应变信息[9-15]。关于DIC技术探究木材干燥形变，目前主要研究报道：李全腾[16]研究发现榆木单板正负应变速率与吸湿解吸速率呈正相关；Kang等[17]发现窑干下西部铁杉和白橡小试块弦径向应变随平均含水率降低而增大；Han等[18]发现窑干下小红松试块收缩形变与含水率呈函数关系；Kang等[19]研究红橡不同含水率下应变速率制定出窑干时间表。上述研究多集中在板材和小试块，对方材的应变规律的研究则未见报道。方材尺寸有别于板材，其干缩异向性差异更大、更易发生开裂变形，故精确监测干燥过程中含水率分布与应力应变信息，解析应变规律及预测开裂出现的时机，可为干燥过程精准实施湿热处理提供参考。

本研究以横截面50 mm×80 mm榆木方材为对象，通过DIC技术实时在线监测不同温度（40、60、80 °C）下榆木方材端面横纹全场应变分布，利用切片法测量方材含水率分布，分析不同温度下弦径向应变规律及其差异，研究含水率分布、应变规律及开裂间联系，为榆木干燥应变机理及干燥工艺优化提供数据支撑。

1 材料与方法

1.1 材料

大兴安岭70年生榆木（Ulmus pumila），气干密度0.70 g/cm3，原木加工成规格2 000 mm（长度方向）×80 mm（弦向）×50 mm（径向）方材。按图1锯切成300 mm（长度方向）×80 mm（弦向）×50 mm（径向）的方材30块，选取24块无节子、虫蛀等缺陷的方材用于本次试验，图1中所有方材尺寸单位均为mm，进行3次重复试验，方材1用于DIC全程拍摄，方材2用于全程含水率检测，方材3—方材8用于含水率约为100%、40%、30%、20%、15%、10%时含水率分布检测，图1中未标号方材作为试验备用材。

试验仪器有DHS-225型恒温恒湿干燥箱、VID-3D非接触全场应变测量系统、101-2AB型电热鼓风箱和电子天平等。

采用表1的干燥条件对试材进行干燥，用图2中的 DIC全场应变测量系统对方材1进行干燥过程中实时拍照。

1.2 方法

1.2.1 形变检测

DIC应变测量系统通过高速摄像机对试件表面散斑图像进行跟踪，试验中所用DIC应变测量系统已自动计算玻璃、空气介质等其他因素对成像过程的影响，所以试验过程中可忽略偏差，并由图像上散斑点位置变化计算试材的位移和应变，图3为弦（R）、径向（T）应变测量位置。试验前，榆木方材横截面应经细砂纸打磨光滑，在试材横截面上均匀涂布白色底漆，随后涂布大小一致的黑色散斑点，通过产生的黑色散斑与白色对比色来提高光学测量的准确性。试验研究已验证，漆膜厚度1 mm内情况下，板材干燥速率、含水率分布与未喷漆对照材相比，未出现差异。试材散斑制备后，在DIC拍摄系统Snap 9软件中调节照片拍摄质量。适当调整相机位置、拍摄角度以及焦距，保证试材拍摄完整性和清晰度；调节适当亮度的灯光保障拍摄图像质量；之后，采用合适校准板拍摄25张校准图片，进行图像校准处理，建立图像分析坐标系；校正图片完成后，采用表2中设置拍摄总时间、时间间隔等参数进行拍摄。

1.2.2 含水率检测

DIC技术要求测量对象在建立图像三维分析坐标系后不能移动，以免影响试验数据的精确可靠性。故试验选用一批纹理结构相同、初含水率接近的方材在同样温湿度下分别进行DIC检测与含水率测定。方材2，由其初重及其两端截取的初含水率试片的初重和绝干重，计算推定出绝干重（干燥结束后用更接近实际的绝干重置换），干燥过程定期取出称重，由式（1）计算其平均含水率，绘出干燥曲线；干燥过程不同阶段（方材2平均含水率约为100%、40%、30%、20%、15%、10%时）依次取出含水率分布检验材（每一阶段取出一块）。图4为去10 mm端头后（试验已证明10 mm厚度内应变大小无明显差异）在同侧切下20 mm厚度含水率分布试片，将其平均分成25块，测量当时重量和绝干重量，由式（1）计算各试块含水率，分析含水率分布。含水率分布检验材余下部分补足长度后放回原位，以保证各试材表面干燥介质流速不受影响。

MCi=Gi-GdGd×100%。（1）

式中：MCi表示i时刻方材或试块含水率；Gi为方材或试块干燥至i时刻重量;Gd为方材或试块绝干重。

2 结果与分析

2.1 不同温度下方材含水率变化规律

图5为干燥过程中榆木方材干燥曲线及其拟合曲线。3组温度下相同含水率变化范围内（含水率由100%降至8%）的平均干燥速率为0.71%、1.02%、1.27%，表明干燥速率随温度升高而明显加快。

原因分析：3种干燥条件，干湿球温差很小，而温度升高的干燥条件，干燥介质相对湿度大、水蒸气分压高，因而试材水分蒸发强度略降。然而，制约试材干燥速率的不是表面或移动蒸发界面水分蒸发的快慢，而是内部水分向移动蒸发界面的迁移速率。温度升高，木材内部水蒸气压力升高、自由水黏度降低、结合水擴散系数增大，促进水分向蒸发界面渗流及扩散，故高温下干燥速率更快。图6为试材干燥过程6个时段与应变检测等同横截面的含水率分布。由图6可知，干燥过程中含水率分布呈中间大边缘小的趋势。40 ℃下方材含水率分布较均匀，未出现较大含水率梯度；60 ℃下逐渐出现梯度（含水率至约10%时，内部含水率超过18%，外部在8%左右）；80 ℃下出现较大梯度（含水率至约15%时，内部含水率超过25%，外部在7%左右）。拟合曲线得出3组温度下榆木方材含水率与干燥时间的函数关系如式（2）—式（4）所示。

MCt=119.65-2.97t+0.026t2-0.000 08t3。（2）

MCt=114.46-4.41t+0.083t2-0.000 69t3。（3）

MCt=109.26-5.84t+0.14t2-0.001 30t3。（4）

式中：MCt表示在t时刻的含水率；t为干燥时间。

拟合函数方程决定系数在0.99以上，相关性高，表明用其描述对应温度下含水率与干燥时间的关系是精准可靠的。

2.2 不同温度下榆木方材横截面全场应变分布规律

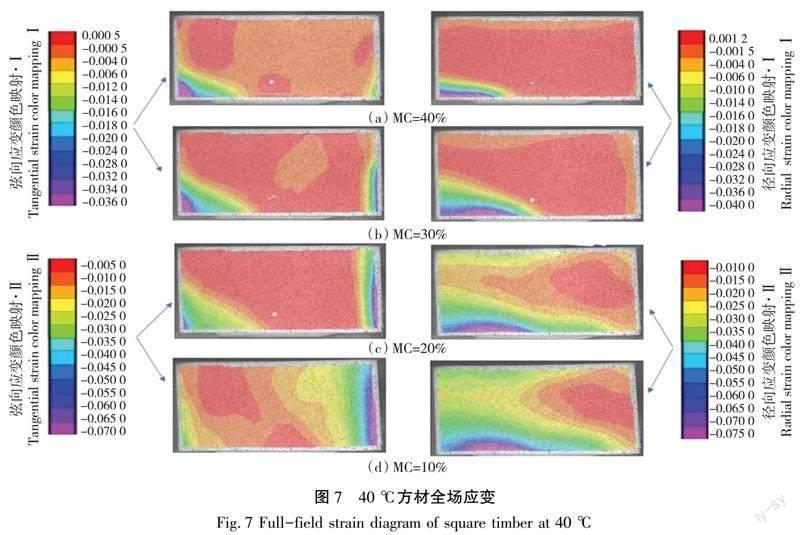
图7—图9为3组温度下榆木方材横截面上全场应变。干燥初期，方材弦径向应变均较小，随干燥进行全场应变分布弦向呈左右高中间低的分布趋势，径向呈上下高中间低的分布趋势。方材在40 ℃下未出现开裂，方材处于高含水率状态时尺寸几乎不变，接近纤维饱和点时，弦径向应变分别为0.004 1、0.002 5，至含水率约15%时弦径向应变增至0.031 5、0.028 3，干燥终了时方材弦径向应变最大分别为0.036 6、0.033 6；60 ℃下含水率约80%时弦径向应变分别为0.010 9、0.009 6，至20%左右时，增至0.041 2、0.031 9，含水率至15%时出现开裂，至10%时开裂加剧并向内延伸，干燥终了时方材弦径向应变最大分别为0.045 2、0.042 3；80 ℃下方材弦向应变快速提升，含水率约30%时为0.044 1，超过径向应变0.037 6，出现开裂，至约15%时开裂加剧并向内延伸，干燥终了时方材弦径向应变最大为0.059 8、0.051 1。由图8可知，开裂处位于颜色映射差别较大处，此时裂纹左端靠内侧应变在0.020 0左右，而右端靠外侧应变则在0.040 0左右；由图9可知，裂纹左端靠内侧应变在0.020 0左右，而右端靠外侧应变则在0.055 0左右；由此可知方材内部存在内外应变差异，且内外应变差异较大的位置易产生开裂。此现象表明高温下榆木方材内外层收缩差异性大，方材外层温度高内层温度低，外层含水率低于内层，外层收缩大内层收缩小故产生热应力，干燥初期方材外部含水率先低于纤维饱和点先开裂；随干燥进行方材外部含水率低，外层应变大，向内部收缩，而方材内部含水率高，抑制方材的收缩，故产生应变差，随即导致方材出现开裂。

2.3 不同温度下弦径向应变及差异分析

应变分布虽可直观显示榆木方材干燥不同时刻应变情况，但难以有效揭示干燥全过程方材应变规律，图10给出不同温度下整体干燥过程的弦径向应变变化及差异曲线：40 ℃下方材弦向应变一直大于径向应变，应变幅度小；60 ℃下方材弦向应变先小后大于径向应变，含水率约30%时应变发生转变，出现交叉点，随后含水率约15%时开裂；80 ℃下方材弦向应变也先小后大于径向应变，应变变向，交叉点出现在含水率约40%时，随后含水率约30%时开裂。

低温下应变规律简单、不变向且方材未开裂；随温度升高应变规律复杂、交叉点出现时机提前。此现象表明，由于方材厚度小于宽度且水分径向移动速率大于弦向，因此干燥前期径向应变大于弦向；随着干燥进行，含水率继续下降，厚度方向水分移动开始缓慢而宽度上水分继续移动且弦向干缩应变大于径向应变，因此干燥后期弦向应变大于径向应变；故高温下，弦径向应变出现交叉点且不同干燥温度下，交叉点出现时机不同：温度越高，出现交叉点的时机越提前。

结合图6—图9可知，60 ℃与80 ℃下出现交叉点后含水率再分别下降15%与10%时，会产生开裂。且通过Logistic拟合得出60、80 ℃温度下榆木方材弦、径向应变与含水率的对应关系式（5）—式（8），据此拟合曲线方程可以获得对应含水率下弦径向应变交叉点出现时机，进而為后续湿热处理时机提供参考。

60 ℃下弦向应变与含水率关系

Y=0.019 2-0.027/（1+x/9.0011.021）。（5）

60 ℃下径向应变与含水率关系

Y=0.052 1-0.089/（1+x/1.9820.592）。（6）

80 ℃下弦向应变与含水率关系

Y=0.029 5-0.042/（1+x/10.2540.095）。（7）

80 ℃下径向应变与含水率关系

Y=0.061 2-0.062 8/（1+x/3.1541.002）。（8）

式中：Y表示在x含水率时的应变；x为含水率。

图11给出不同温度下不同含水率时弦径向应变一阶导数值，含水率30%以上时弦径向应变一阶导数值均不超过0.003 0；60 ℃下弦径向一阶导数最大值分别为0.007 5、0.007 7；80 ℃下弦径向一阶导数最大值分别为0.008 1、0.008 8。3组温度下，一阶导数值随温度升高、含水率降低而变大。一阶导数值大小代表同一含水率变化量区间内应变变化速率，上述应变变化规律与开裂间关系，可以证明导数值越大说明应变变化速率越快；温度越高，弦径向应变变化速率越快：温度升高引起方材内部含水率梯度的增大导致干燥应力增速加快，高温度下方材干缩应变变化速率大，故方材快速收缩易产生开裂等缺陷。

3 结论

利用DIC在线、实时检测干燥过程中榆木方材横截面上位移与应变变化规律，得到如下结论：40 ℃时方材未开裂，弦径向应变未出现交叉点，弦径向最大应变值分别为0.036 6、0.033 6；60 ℃时含水率约30%时出现交叉点，含水率约15%时开裂，弦径向应变值分别约为0.040 5、0.035 7，裂纹产生于含水率梯度差异较大区域（内部含水率超过18%，外部在9%左右），开裂由外向内延伸，干燥终了弦径向应变分别为0.042 3、0.045 2；80 ℃时含水率约40%时出现交叉点，含水率约30%时开裂，弦径向应变值分别约为0.044 1、0.037 6，裂纹产生于含水率梯度差异较大区域（内部含水率超过25%，外部在7%左右），干燥终了弦径向应变分别为0.059 8、0.051 1。由此可知，温度对榆木方材的应变及其分布影响显著（P＜0.05）；方材干燥过程中开裂时机与弦径向应变变向交叉点出现时机存在对应关系，所以可以通过观察干燥过程中应变变化推测开裂时机，并在产生开裂前，对木材进行相应处理，达到完善干燥工艺、提高干燥质量的目的。

【参 考 文 献】

[1]王旭婷，崔力庆，宋魁彦.榆木微观构造及其分形设计图像的纹理研究[J].林业机械与木工设备，2018，46（1）：35-37，40.

WANG X T， CUI L Q， SONG K Y. Research on the microstructure on elm and the texture of its fractal design images[J]. Forestry Machinery & Woodworking Equipment， 2018， 46（1）： 35-37， 40.

[2]刘瑞锋.水热处理对榆木力学性质及旋切薄木表面粗糙度影响的研究[D].呼和浩特：内蒙古农业大学，2015.

LIU R F. Study on the influence of hydrothermal treatment on the mechanical properties of Ulmus pumila and the surface roughness of rotary-cut veneer[D]. Hohhot： Inner Mongolia Agricultural University， 2015.

[3]杨永强，赵西平，郭平平，等.大果榆全树木材解剖特征及纤维形态的研究[J].西部林业科学，2022，51（3）：74-80.

YANG Y Q， ZHAO X P， GUO P P， et al. Wood anatomical characteristics and fiber morphology of Ulmus macrocarpa[J]. Journal of West China Forestry Science， 2022， 51（3）： 74-80.

[4]付宗营.常规干燥过程中白桦树盘干燥应力应变的研究[D].哈尔滨：东北林业大学，2017.

FU Z Y. Study on drying stress and strain of Betula platyphylla in conventional drying process[D]. Harbin： Northeast Forestry University， 2017.

[5]赵景尧，蔡英春，付宗营.白桦树盘生长特性对干燥开裂的影响[J].林业科学，2013，49（7）：129-135.

ZHAO J Y， CAI Y C， FU Z Y. Effect of white birch disk characteristics on drying check behaviors[J]. Scientia Silvae Sinicae， 2013， 49（7）： 129-135.

[6]李安鑫，吕建雄，蒋佳荔.木材细胞壁结构及其流变特性研究进展[J].林业科学，2017，53（12）：136-143.

LI A X， LYU J X， JIANG J L. A review of wood cell wall structure and its rheological property[J]. Scientia Silvae Sinicae， 2017， 53（12）： 136-143.

[7]李大纲.国内外木材干燥应力研究现状及发展趋势[J].建筑人造板，2001（2）：15-19.

LI D G. Research status and development trend of wood drying stress at home and abroad[J]. Building Artificial Boards， 2001（2）： 15-19.

[8]YAMASHITA K， HIRAKAWA Y， NAKATANI H， et al. Tangential and radial shrinkage variation within trees in sugi （Cryptomeria japonica） cultivars[J]. Journal of Wood Science， 2009， 55（3）： 161-168.

[9]邵環.微波处理木材干燥应变的研究[D].呼和浩特：内蒙古农业大学，2010.

SHAO H. Study on drying strain of wood treated by microwave[D]. Hohhot： Inner Mongolia Agricultural University， 2010.

[10]张燕，宋魁彦，佟达.复配碱液处理榆木顺纹压缩应力-应变本构关系[J].林业科学，2012，48（11）：83-86.

ZHANG Y， SONG K Y， TONG D. Stress-strain constitutive relations of longitudinal compressed elm wood with compound alkali liquor processing[J]. Scientia Silvae Sinicae， 2012， 48（11）： 83-86.

[11]赵景尧，蔡英春.数字图像相关技术及其在木材科学研究中的应用[J].世界林业研究，2015，28（6）：53-57.

ZHAO J Y， CAI Y C. Digital image correlation technology and its application to wood science[J]. World Forestry Research， 2015， 28（6）： 53-57.

[12]江泽慧，费本华，张东升，等.数字散斑相关方法在木材科学中的应用及展望[J].中国工程科学，2003，5（11）：1-7.

JIANG Z H， FEI B H， ZHANG D S， et al. Application and prospect of digital speckle correlation method on wood science[J]. Engineering Science， 2003， 5（11）： 1-7.

[13]FU Z Y， WENG X， GAO Y F， et al. Full-field tracking and analysis of shrinkage strain during moisture content loss in wood[J]. Holzforschung， 2021， 75（5）： 436-443.

[14]李霞镇，任海青，马少鹏.基于数字散斑相关方法的竹材变形特性[J].林业科学，2012，48（9）：115-119.

LI X Z， REN H Q， MA S P. Deformation behavior of bamboo based on DSCM[J]. Scientia Silvae Sinicae， 2012， 48（9）： 115-119.

[15]PENG M K， HO Y C， WANG W C， et al. Measurement of wood shrinkage in jack pine using three dimensional digital image correlation （DIC）[J]. Holzforschung， 2012， 66（5）： 639-643.

[16]李全腾.利用DIC技术研究木材单板吸湿解吸过程中的应变[D].呼和浩特：内蒙古农业大学，2020.

LI Q T. Study on the strain of wood veneer during moisture absorption and desorption by DIC technology[D]. Hohhot： Inner Mongolia Agricultural University， 2020.

[17]KANG H Y， MUSZYA L， MILOTA M R. Optical measurement of deformations in drying lumber[J]. Drying Technology， 2011， 29（2）： 127-134.

[18]HAN Y， PARK Y， PARK J H， et al. The shrinkage properties of red pine wood assessed by image analysis and near-infrared spectroscopy[J]. Drying Technology， 2016， 34（13）： 1613-1620.

[19]KANG C W， MUSZYA L， HONG S H， et al. Preliminary tests for the application of an optical measurement system for the development of a kiln-drying schedule[J]. Drying Technology， 2016， 34（4）： 483-490.