分布式驱动电动汽车附着稳定性控制

张文通,孙 文,2,,王军年,张 屹,赵景波,2

(1.常州大学 机械与轨道交通学院,江苏 常州 213164;2.常州工学院 汽车工程学院, 江苏 常州 213032;3.吉林大学 汽车仿真与控制国家重点实验室, 长春 130022)

0 引言

随着传统能源日趋枯竭与环境污染日渐加重,在汽车领域,以电机为驱动装置的电动汽车将逐渐取代以发动机为动力源的传统燃油汽车。如今,电动汽车正迎来飞速发展,其操纵稳定性、安全性一直为人们所关注。分布式驱动电动汽车由于其传动链短、传递效率高、电机响应迅速以及四轮转矩可解耦,在提高车辆极限工况下的操纵稳定性与安全性方面具有突出优势,成为国内外学者的重点研究对象[1-2]。

在极限工况下,由于轮胎与地面之间存在的非线性耦合特性,简单的转矩分配方式难以满足车辆附着稳定性要求。针对车辆附着稳定性问题,国内外研究主要集中在改善控制策略结构、提高控制算法性能和优化转矩分配目标函数等方面。

在改善控制策略结构方面:欧健等[3]基于滑模控制与电液协调系统,制定分层式横摆稳定性控制策略,通过NI硬件在环系统进行验证。Chen等[4]搭建电子稳定程序和动态转矩分配系统的递阶协调控制模型,进行性能仿真测试和硬件在环实验。Zhu等[5]针对低摩擦系数路面上轮胎的动态特性,在主动安全控制层调节前轮转角和附加横摆力矩,根据驾驶员动态需求和执行器约束,在能效控制层设计模型预测控制的转矩分配控制器。在提高控制算法性能方面:黄彩霞等[6]基于区域极点配置方法,分析设计权重矩阵参数,制定了轮毂电机转矩分配横摆稳定性控制策略。Guo等[7]采用自适应分层控制架构轨迹跟踪方法,上层通过滑模控制器求解所需前轮转角和附加横摆力矩,下层采用伪逆控制算法对四轮转矩优化分配。Liu等[8]提出了一种动态直接横摆力矩控制器,采用数据融合技术,利用无迹粒子滤波器估计侧偏角与横摆角速度,实现车辆纵向、横向稳定性。Wei等[9]提出了一种基于深度强化学习的转矩分配策略,并采用一种双延迟的深确定性策略梯度算法以降低能耗。在优化转矩分配目标函数方面:张雷等[10]采用分层架构轨迹跟踪与直接横摆力矩协调控制策略,考虑系统多约束非线性问题,以轮胎负荷率最小对四轮转矩优化分配。王军年等[11]针对车轮滑转率的抑制和过弯性能的改善问题,提出了一种基于轮胎纵向刚度估计和最佳滑转率识别的转矩分配控制策略。但在现有研究中,很少从车轮垂向载荷转移影响轮胎附着裕度的角度,来分析对车辆的附着稳定性的影响,因而本文对车辆主动安全控制技术的发展具有一定的探究意义。

本文从轮胎与地面动力学特性变化造成车轮垂向载荷转移,引起轮胎附着裕度改变的角度出发,分析了影响车辆附着稳定性的因素。采用分层式控制结构,上层以横摆角速度与质心侧偏角为控制目标,求出需求附加横摆力矩,下层根据垂向载荷比例分配四轮转矩,以实现车辆附着稳定性控制。通过构建Matlab/Simulink与CarSim联合仿真测试平台和搭建dSPACE LabBox与Matlab/Simulink、CarSim驾驶模拟器台架的硬件在环实验平台,对不同转矩分配方式下车辆附着稳定性相关评价指标进行对比分析,以验证转矩分配方案的合理性与控制策略的有效性。

1 车轮垂向载荷与附着裕度机理

1.1 车轮垂向载荷转移对附着裕度影响分析

车辆模型以整车质心为原点,建立坐标系oxyz,如图1所示。

图1 车辆模型坐标图

图1中:Fxij、Fyij分别为各轮纵向力、侧向力;δij为各轮转角;αij为各轮侧偏角;vxij为各轮速度;vx、vy分别为纵向车速、侧向车速;V为质心速度;β为质心侧偏角;r为横摆角速度;d为轮距;a、b分别为质心到前轴、后轴的距离;l=a+b为前后轴距;ij=fl、fr、rl、rr分别为左前轮、右前轮、左后轮、右后轮。

沿x轴的纵向运动:

Fxrl+Fxrr-Fyflsinδfl-Fyfrsinδfr

(1)

沿y轴的侧向运动:

Fyrl+Fyrr+Fxflsinδfl+Fxfrsinδfr

(2)

绕z轴的横摆运动:

Fxflsinδfl+Fxfrsinδfr)a-(Fyrl+Fyrr)b+

(Fxfrcosδfr-Fxflcosδfl+Fyflsinδfl-

Fyfrsinδfr+Fxrr-Fxrl)d/2

(3)

式中:m为整车质量;Iz为绕z轴转动惯量。

各轮垂向载荷:

(4)

式中:Fzij为各轮垂向载荷;ax、ay分别为纵向加速度、侧向加速度;h为质心高度;g为重力加速度。

由式(4)可知,车辆受驾驶员加、减速及转向操纵,车轮垂向载荷发生转移。由于纵向力与侧向力高度耦合,当某一车轮垂向载荷增大,其所能利用的极限附着力增大,反映在附着椭圆边界范围变大,说明该车轮拥有更大的附着裕度。在车辆附着稳定性控制时,应充分利用垂向载荷大的车轮具有附着裕度较大的特性,对其施加较大的驱动转矩,以避免轮胎处于非线性区时,受附着椭圆约束而达到饱和极限,造成车辆失稳。

附着椭圆可表述为:

(5)

式中,μ为路面附着系数。

为了充分体现车辆附着稳定性的控制效果以及考虑轮胎非线性特性对附着裕度的影响,引入轮胎附着率[12]:

(6)

式中,ρij为各轮附着率。

由式(6)可知,轮胎附着率反映了车轮对地面的附着利用情况,附着率越小,附着裕度越大,附着稳定性越好。但四轮附着率难以实现同时降低,通常会由于某一车轮附着率降低,引起其他车轮附着率提高。因而,应降低高附车轮附着率,以避免达到附着极限;提高低附车轮附着率,以充分利用地面提供的附着条件。

为了反映各轮附着裕度大小,定义轮胎附着率偏离程度,作为车辆附着稳定性的评价指标:

(7)

式中,S为轮胎附着率偏离程度,反映各轮附着率的离散情况。

1.2 根据垂向载荷比例分配转矩合理性验证

选取“U”型弯道作为仿真工况,采用2组实验对比方案,将根据垂向载荷比例分配四轮转矩方式与平均分配四轮转矩方式进行车辆附着稳定性合理性验证。

方案1:入弯半径为90 m,车辆分别以40、60、80 km/h匀速行驶。

方案2:入弯半径分别为50、90 m,车辆以 60 km/h匀速行驶。

为了描述车轮垂向载荷转移对附着稳定性的影响,对部分参数仿真结果作说明:

1) 行驶轨迹。车辆行驶轨迹基本重合。

2) 前轮转角。当车辆行驶在直线路段时,2种转矩分配方式下前轮转角基本相同。当车辆驶入弯道路段时,根据垂向载荷比例分配四轮转矩方式前轮转角比平均分配四轮转矩方式要小,并表现为:当入弯半径相同时,车速越大,或当车速相同时,入弯半径越小,2种转矩分配方式下的前轮转角偏差均变大。

3) 横摆角速度与质心侧偏角。2种转矩分配方式下车辆行驶轨迹一致,其横摆角速度趋于重合。根据垂向载荷比例分配四轮转矩方式比平均分配四轮转矩方式在入弯处的质心侧偏角更大,并表现为:当入弯半径相同时,车速越大,或当车速相同时,入弯半径越小,2种转矩分配方式下的质心侧偏角偏差均变大。

4) 总的轮胎附着率。2种分配方式下总的轮胎附着率基本相同,说明根据垂向载荷比例分配四轮转矩方式并未降低总的轮胎附着率,不能反映车辆附着稳定性好坏。

当车辆行驶在直线路段时,根据垂向载荷比例分配四轮转矩方式的各轮附着率十分接近,而平均分配四轮转矩方式出现了较大的附着率偏差。当车辆驶入弯道路段时,2种转矩分配方式都表现为:当入弯半径相同,车速越大,或当车速相同,入弯半径越小,各轮附着率均变大。如图2—5分别为4次仿真测试下各轮附着率曲线。

图2 入弯半径90 m、车速40 km/h的四轮附着率

图3 入弯半径90 m、车速60 km/h的四轮附着率

图5 入弯半径50 m、车速60 km/h的四轮附着率

其中,红色表示平均分配四轮转矩方式,蓝色表示根据垂向载荷比例分配四轮转矩方式,且LF、RF、LR、RR分别表示左前轮、右前轮、左后轮、右后轮,分别用实线、虚线、点线、点划线区分。

根据垂向载荷比例分配四轮转矩方式比平均分配四轮转矩方式在均衡各轮附着率方面更具优势,表现为:当入弯半径相同,车速越大,或当车速相同,入弯半径越小,其在改善轮胎附着裕度方面效果越明显。图6—9分别为4次仿真测试下轮胎附着率偏离程度曲线。

图6 入弯半径90 m、车速40 km/h的附着率偏离程度

图7 入弯半径90 m、车速60 km/h的附着率偏离程度

图8 入弯半径90 m、车速80 km/h的附着率偏离程度

图9 入弯半径50 m、车速60 km/h的附着率偏离程度

图中,平均分配指平均分配四轮转矩方式,垂载分配指根据垂向载荷比例分配四轮转矩方式。

通过上述分析表明:根据垂向载荷比例分配四轮转矩方式相比于平均分配四轮转矩方式,不仅降低了高附车轮附着率,提升其附着裕度,也提高了低附车轮附着率,改善其附着利用情况。考虑车轮垂向载荷转移对轮胎附着裕度的影响,根据垂向载荷比例分配四轮转矩可提高车辆的附着稳定性。

2 车辆附着稳定性控制器设计

为了进一步说明根据垂向载荷比例分配四轮转矩在改善车辆附着稳定性和避免过大横摆力矩使车辆偏离期望行驶轨迹方面的优势,引入直接横摆力矩控制,通过附加横摆力矩修正车身姿态,从而更大程度地提高车辆附着稳定性。

由于附加横摆力矩是通过调节各轮驱动转矩输出大小产生的,可根据车辆的实际运动状态、驾驶员的驾驶意图和轮胎的附着特性等有针对性地实时调节车辆行驶状态,改善其转弯行驶过程中的机动性和稳定性。在车辆行驶过程中,质心侧偏角与横摆角速度是车辆稳定性的重要表征参数,因而将这2个参数作为控制器设计的控制目标。

2.1 上层-附加横摆力矩决策层

2.1.1参考模型

线性2自由度车辆模型结构简单、计算效率高、参数响应快,常被用于车辆动力学研究的基础模型。为了得到期望的质心侧偏角与横摆角速度,本文将其作为参考模型。

针对参考模型作如下假设:忽略转向和悬架系统,以前轮转角为输入,只做平行于地面的运动;忽略空气阻力和滚动阻力,以及左右轮间载荷转移对轮胎特性的影响;假设驱动力很小,并沿x轴方向纵向车速不变;侧向加速度限定在0.4g以下,轮胎侧偏特性处于线性范围内。

参考模型以整车质心为原点,建立坐标系oxyz,如图10所示。

图10 参考模型坐标图

沿y轴的侧向运动:

(8)

绕z轴的横摆运动:

(9)

式中:Fyf、Fyr分别为前、后轮侧向力;δ为前轮转角;vxf、vxr分别为前、后轮速度;αf、αr分别为前、后轮侧偏角;Cf、Cr分别为前、后轮侧偏刚度。

当车辆做等速圆周运动时,产生的质心侧偏角与横摆角速度的响应值即为期望值:

(10)

(11)

式中:K=m(a/Cr-b/Cf)/l2为稳定性因数;βd、rd分别为期望的质心侧偏角与横摆角速度。

在此工况下,参考模型的侧向加速度:

(12)

式中,R为车轮半径。

在实际行驶过程中,车轮受到路面附着条件约束,当侧偏角不断增大,轮胎易进入非线性区,此时侧向加速度满足:

ay≤0.85μg

(13)

当轮胎处于非线性区时,期望的质心侧偏角与横摆角速度满足:

βdmax=arctan(0.02μg)

(14)

rdmax=0.85μg/vx

(15)

因而,期望质心侧偏角与横摆角速度:

(16)

(17)

具有附加横摆力矩的状态空间方程[13]:

(18)

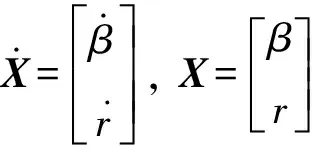
2.1.2模型预测控制

模型预测控制具有较强的鲁棒性,善于解决系统多输入输出问题,以及各种不可预测因素对车辆稳定性的干扰。通过实时滚动优化,将实际测得的车辆参数反馈矫正,使预测值趋近当前系统状态的期望值。

对式(18)进行离散化处理:

(19)

假设控制时域步长等于预测时域步长,则在预测时域内的控制输出:

(20)

为了减小计算量和提高效率,假设所有时刻系统期望控制输出与控制输入在预测时域内保持不变。根据选取的控制目标,使实际值趋近期望值,构建目标函数[14-15]:

(21)

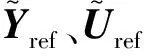
将式(21)展开得:

(22)

式中,Yk、Uk分别为k时刻的预测输出与控制输入。

为了方便计算,采用二次规划方法对控制目标函数进行求解:

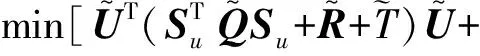
(23)

2.2 下层-四轮转矩优化分配层

车辆行驶产生的横摆力矩由轮胎所受纵向力、侧向力共同作用产生。分布式驱动电动汽车各轮纵向力可通过人为直接输出转矩进行独立控制,而侧向力是通过转向系统进行间接控制。为了得到符合驾驶员驾驶意图且直接可控的附加横摆力矩,这里仅考虑通过调控输出转矩产生的纵向力,对整车形成的附加横摆力矩进行优化分配。

由于车轮垂向载荷转移对轮胎附着裕度的影响,制定根据垂向载荷比例分配四轮转矩的优化目标函数。

目标函数1:在平均分配四轮转矩基础上,根据垂向载荷比例分配附加横摆力矩。

(24)

目标函数2:在根据垂向载荷比例分配四轮转矩基础上,对附加横摆力矩根据垂向载荷比例进行再次分配。

(25)

式中:Tdes为总的需求转矩;Tij为各轮输出转矩;∑FZij为总的垂向载荷。

3 仿真分析与实验验证

3.1 CarSim整车模型构建

选取CarSim车辆模型库中的“B-Class,Hatchback”作为离线仿真测试与硬件在环实验的整车模型,整车参数如表1所示。

表1 整车参数

由于CarSim目前仅有针对传统燃油汽车或混合动力汽车的整车模型,尚缺少纯电动汽车整车模型。为了验证控制策略的有效性,基于Matlab/Simulink平台搭建电机与电池模型,并将CarSim整车模型中的传动系统,包括发动机、差速器等部件截断,外接搭建的电机与电池模型。电机模型是依据电机的转矩、转速等基本参数构建MAP图,再通过查表的方式建立的,电池模型也采用查表法搭建而成。

为了验证所搭建的整车模型的准确性与有效性,本文将仅使用CarSim整车模型作为对照组,采用相同的动力输出方式。通过仿真结果对比分析,输出的相关参数基本一致,说明所搭建的整车模型是有效的,可作为验证控制策略的基础车辆模型。但由于整车模型的搭建并不是研究重点,其相关验证过程不作过多阐述。

3.2 分层式控制策略平台搭建

根据所制定的分层式控制策略,搭建离线仿真测试与硬件在环实验平台流程如图11所示[16-17]。

所制定的控制策略在车轮垂向载荷转移引起轮胎附着裕度变化机理分析与仿真测试基础上,设计由附加横摆力矩决策层与四轮转矩优化分配层组成的分层式控制器。附加横摆力矩决策层以车轮转角、纵向车速为参考模型输入,求解期望的质心侧偏角与横摆角速度,并与CarSim模型输出的实际值形成偏差,作为模型预测控制器输入,求解维持车辆附着稳定所需的附加横摆力矩。四轮转矩优化分配层根据车轮垂向载荷比例构建优化目标函数,将上层求得的附加横摆力矩分配给各轮,提高附着稳定性。

通过搭建Matlab/Simulink与CarSim联合仿真测试平台,对控制策略进行离线仿真测试,并基于硬件在环系统进行HIL在线实验验证。

3.3 控制策略仿真分析

离线仿真测试选取“J”型弯道工况,车辆以 90 km/h匀速行驶,入弯半径为80 m,仿真时长为12 s。

针对以下曲线作如下说明:平均、垂载、平均+垂载、垂载+垂载分别指平均分配四轮转矩、根据垂向载荷比例分配四轮转矩、根据目标函数1分配四轮转矩、根据目标函数2分配四轮转矩,且分别用红色实线、蓝色虚线、绿色点划线、黑色点线区分,且左前轮、右前轮、左后轮、右后轮附着率分别用实线、虚线、点划线、点线区分。

4组仿真测试下车辆行驶轨迹基本重合,未发生失稳,如图12所示。

当车辆行驶在直线路段时,4种转矩分配方式下前轮转角都很小且基本重合。当车辆驶入弯道路段时,平均、垂载+垂载产生了更大的前轮转角,最大值分别为0.071、0.074 rad,而平均+垂载产生的前轮转角最小,最大值仅为0.051 rad,如图13所示。

图13 前轮转角曲线

当车辆行驶在直线路段时,4种转矩分配方式下各轮附着率都很小,且总的附着率基本相同。当车辆驶入弯道路段时,平均、垂载+垂载的附着率偏离程度最大,最大值分别为18.37%、16.15%,此时车辆具有较差的附着稳定性。而平均+垂载的附着率偏离程度最小,最大值仅为11.34%,明显降低了高附车轮附着率和提高了低附车轮附着率,如图14—16所示。

图14 四轮附着率曲线

图15 总的附着率曲线

图16 附着率偏离程度曲线

通过上述分析可知:当车辆驶入弯道时,平均、垂载+垂载产生的前轮转角更大,且不利于轮胎附着率的合理利用。而平均+垂载比较于其他3种转矩分配方式具有明显的改善轮胎附着裕度的效果,从而提高了车辆的附着稳定性。

3.4 硬件在环实验验证

硬件在环实验选取“直线+弯道”工况,车辆以60 km/h匀速行驶,入弯半径为80 m,仿真时长为40 s。

4种转矩分配方式下的车辆行驶轨迹基本重合,未发生失稳,如图17所示。

图17 行驶轨迹曲线

当车辆行驶在直线路段时,4种转矩分配方式下前轮转角都很小且基本重合。当车辆驶入弯道路段时,平均、垂载、垂载+垂载产生的前轮转角最大值分别为0.041、-0.040、-0.038 rad。而平均+垂载产生的前轮转角最小,最大值仅为0.036 rad,此时车辆具有更好的操纵稳定性,如图18所示。

图18 前轮转角曲线

车辆在行驶过程中,平均+垂载的各轮附着率较为接近,产生的总的附着率较低,且附着率偏离程度最小,最大值仅为2.34%。而平均、垂载+垂载体现出较差的控制效果,其附着率偏离程度最大值分别为3.33%、3.39%。实验结果表明:4种转矩分配方式在改善轮胎的附着裕度和提高车辆的附着稳定性方面的控制效果:平均+垂载>垂载>平均>垂载+垂载,如图19—21所示。

图19 四轮附着率曲线

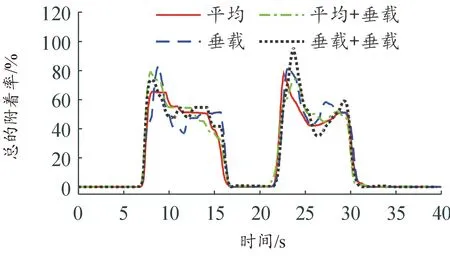
图20 总的附着率曲线

图21 附着率偏离程度曲线

通过离线仿真测试与硬件在环实验结果对比分析,说明了车轮垂向载荷转移对轮胎附着裕度变化的重要影响,验证了根据垂向载荷比例分配四轮转矩的合理性与本文所制定的控制策略在改善车辆附着稳定性方面的有效性。

4 结论

针对提高车辆附着稳定性控制问题,文中从机理上说明了车轮垂向载荷转移对附着裕度的深刻影响,构建了根据车轮垂向载荷比例分配四轮转矩的目标函数,引入直接横摆力矩控制,以实现对车辆的实时调整和修正。仿真测试与硬件在环实验结果表明,验证根据车轮垂向载荷比例分配四轮转矩的直接横摆力矩控制策略能有效提高轮胎的附着裕度,改善车辆的附着稳定性。同时,提出的附着率偏离程度可直观反映各轮附着率的离散情况,在一定程度上可作为车辆附着稳定性的评价指标。