二冲程点燃式航空煤油发动机爆震预测模型研究
2023-06-08杨浩鹏杨海青魏民祥赵卓文
杨浩鹏,杨海青,魏民祥,吴 昊,赵卓文,吴 昭
(1.南京航空航天大学 能源与动力学院, 南京 210016;2.南京长空科技有限公司, 南京 211800)
0 引言
航空活塞发动机以汽油作为燃料已经有很长一段历史,从研究开发到生产制造也发展得非常成熟。但由于汽油饱和蒸气压高、闪点低、挥发性强的特点,使其在储存、运输和使用过程中存在相当大的安全隐患[1]。而航空煤油饱和蒸气压低、不易挥发且闪点较高(45~51 ℃)[2],满足军用燃料一体化的要求,因此航空活塞发动机燃用航空煤油已经成为国防所需。点燃式航空煤油发动机可以在现有航空汽油机的基础上进行改造,研发成本低,并且该类型的发动机能够继承航空汽油机高功重比的优点。
发动机爆震是汽油机改烧煤油过程中不可忽视的技术障碍。相比于汽油,航空煤油的辛烷值(23~51)、自燃温度(240~260 ℃)更低[3],并且航空煤油的火焰传播速度较慢。这使得同样为预混燃烧方式的点燃式航空煤油发动机更容易出现爆震现象。因此,研究以煤油为燃料的航空活塞发动机的爆震问题具有工程实际意义。目前存在多种理论解释产生爆震的原因,但学者们广泛接受的是自燃理论,即在火花塞点火之后,末端混合气在火焰前锋面到达之前自燃的现象。
对于发动机爆震的研究普遍采用试验法和数值模拟的方法。胡春明等[4]对某双火花塞点火的煤油发动机进行试验,发现通过增大异步点火相位差可以降低爆震时的瞬间放热率,能够抑制爆震燃烧,但发动机的动力性能有所下降。Hess等[5]认为末端混合气的自燃与燃烧开始前的预反应有关。他们提出了一种新的标准,将自燃开始之前未燃烧混合物的预反应考虑在内。通过燃用不同辛烷值的汽油机试验进行验证,发现预测的爆震起始曲轴转角精度更高。李志锐等[6]对一台单缸四冲程汽油机进行爆震试验,建立了整机的一维仿真模型。通过对比两类爆震模型的仿真结果,认为现有的爆震模型只能在部分工况下获得较为准确的结果。陈龙华等[7]针对一台增压汽油机建立了同时考虑过量空气系数和废气再循环的爆震预测模型。通过试验数据确定了爆震模型的系数,仿真结果表明该爆震模型的预测性能较好,对不同发动机有较好的适应性。
综上,由于发动机爆震会带来很大的不可控风险,爆震试验只能在有限的工况下进行,近年来采用数值模拟的方法预测爆震现象成为学者们研究的热点。爆震预测模型在汽油机一维仿真模拟过程中的应用已发展得相当成熟[5-9],但是在航空煤油活塞发动机上的应用还并不完善,针对煤油燃料模型参数的设置略显粗糙。此外,在这类模型的应用过程中,燃料的燃烧特性(如层流火焰传播速度等)会对爆震预测精度以及一维仿真模拟的准确度产生较大影响,但相关的研究情况却少有报道。
本文首先介绍了爆震预测模型的建立过程,并分析了模型计算所需的数据,然后基于一款二冲程点燃式航空煤油发动机的爆震试验及相关爆震评价指标,根据已公开的RP-3航空煤油燃烧特性实验数据建立煤油的燃烧模型,以一维仿真软件GT-Power为平台进行模型搭建及验证,利用Matlab软件编写程序评估2种爆震预测模型的预测性能。
1 爆震预测模型
末端混合气自燃引起的压力振荡被作为爆震发生的标志,为了预测爆震发生的时刻,学者们建立了众多数学模型[8-11]。其中基于化学反应动力学模型的爆震预测计算量大,即使是简化的动力学模型也因其庞大的计算量很难应用于工程实际。普遍使用的方法是监测燃料的着火延迟时间,可燃混合气的着火延迟时间τ采用Arrhenius形式的经验公式表示为压力和温度的函数,如式(1)所示。
(1)
式中:τ为着火延迟时间;P和T分别为压力和温度;A、n和B为经验常数。
为了确定爆震是否发生,Livengood等[12]在1957年首次提出了着火延迟积分判断法。这也是最初的爆震预测模型,如式(2)所示,当积分值达到1时,爆震发生时刻为tknock。
(2)
式中:τ为Arrhenius形式的经验公式;tIVC为进气门关闭时刻(对应二冲程发动机为扫气口关闭时刻);tknock为爆震发生时刻。
Douaud等[13]将此方法应用于汽油发动机爆震预测的研究,通过发动机爆震实验数据,开发并验证了着火延迟时间的标准表达式,如式(3)所示。
(3)
式中:FON为燃料辛烷值;P为气缸内压力;T为末端混合气温度。
为了拓宽着火延迟积分预测爆震的应用范围,Swarts等[14]考虑了过量空气系数对着火延迟时间的影响,对标准表达式进行了修正。Hoepke等[15]在标准表达式中引入了EGR率,重新改进了着火延迟时间的表达式,使其能应用于带有废气再循环系统的发动机。
然而这些工作大多是针对以汽油为燃料的发动机开展的,为了研究航空煤油的着火延迟特性,近年来国内外学者[16-19]通过化学激波管实验获得了航空煤油不同温度、压力条件下的着火延迟时间。刘靖等[17]在实验数据的基础上,利用多元线性回归拟合得到了RP-3航空煤油及其多组分替代燃料着火延迟时间关系式,发现两者的着火延迟特性基本吻合,其中RP-3航空煤油的单一Arrhenius形式的着火延迟时间如式(4)所示。
(4)
式中:φ为过量空气系数。
已有研究表明[20],单一Arrhenius形式的着火延迟时间不能反映真实燃料复杂的燃烧放热,Douaud模型只是反映了燃料在中温状态下的着火延迟响应,并不能很好地预测低温或高温状态的自燃反应。考虑到燃料在燃烧放热过程中的复杂性[21],为了反映真实燃料具有的两级放热和负温度系数现象,建立了3-Arrhenius形式的着火延迟时间表达式,以此来模拟末端混合气自燃时的低温、中温和高温状态,如式(5)和式(6)所示。
(5)
(6)
式中:τ1+τ2表示两段低温状态的着火延迟时间;τ3表示高温状态的着火延迟时间。式(6)中,i=1,2或3;Ai、ni和Bi为经验常数,对于这些经验常数,Swarts[14]提出并验证了正庚烷、异辛烷和甲苯这3种燃料的Ai、ni和Bi,分别在表1中列出。
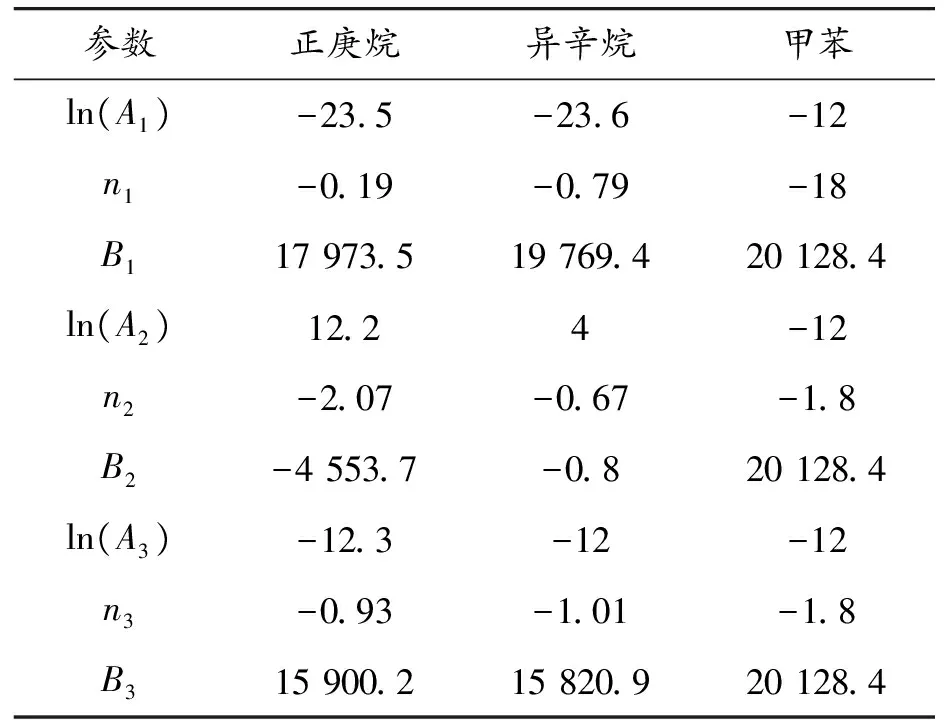
表1 不同燃料的着火延迟模型参数
由于航空煤油化学组分复杂,并且存在负温度系数现象,本文基于式(7)提出了一种由两组分替代燃料计算的航空煤油混合着火延迟时间模型。
(7)
式中:j为燃料组分的编号;vj为燃料组分的体积分数;ω为经验混合指数,取1.14[20]。
根据文献[22]的研究,由89%正庚烷和11%甲苯组成的两组分替代燃料能够近似模拟航空煤油的化学动力学反应机理,并且通过射流搅拌器实验验证了该机理的可靠性。综上所述,根据式(5)—(7)可计算航空煤油的混合着火延迟时间。图1为航空煤油混合着火延迟时间表达式的计算流程,最终得到了航空煤油3-Arrhenius形式的混合着火延迟时间τk。
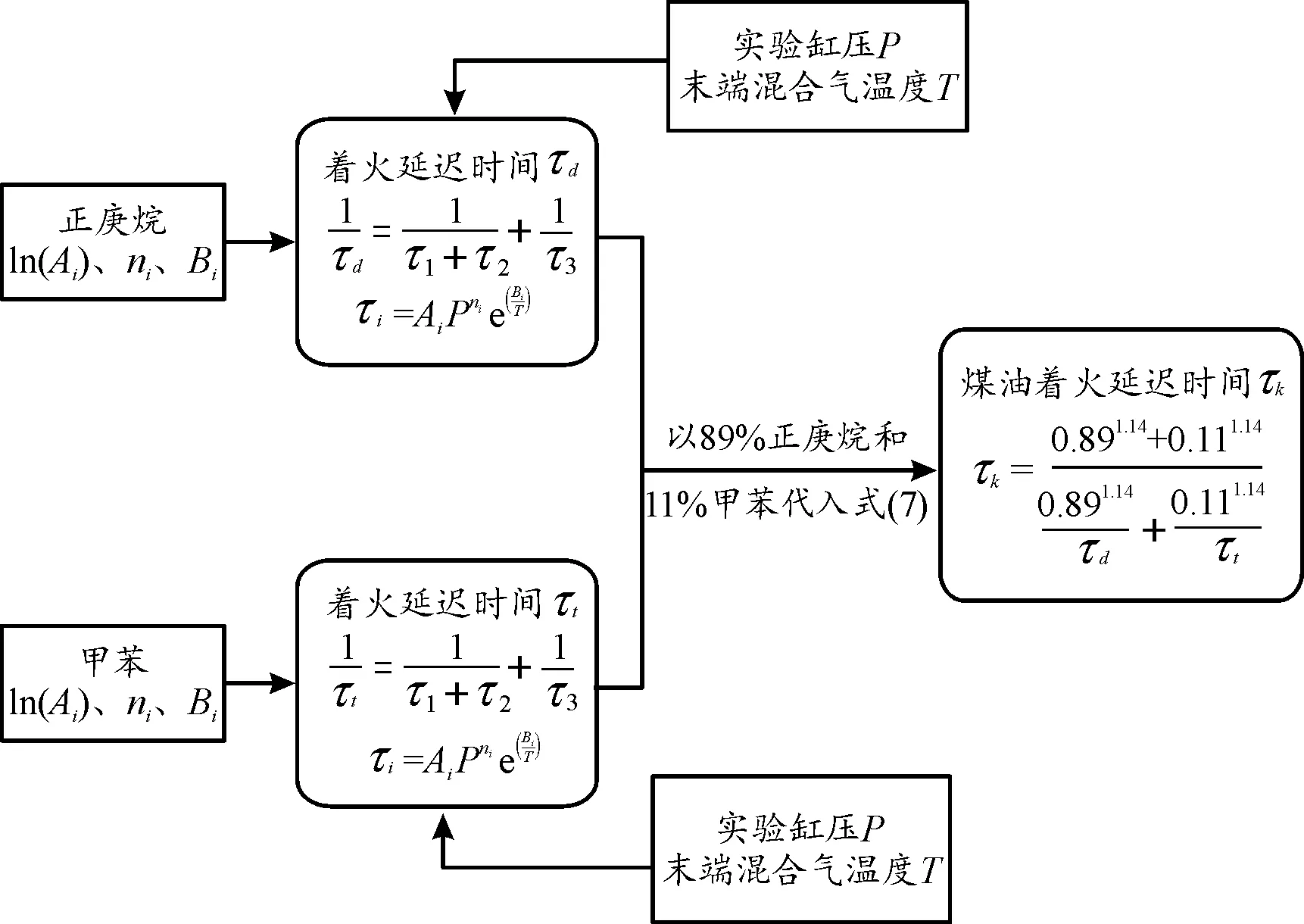
图1 航空煤油混合着火延迟时间计算流程
可以看出缸内压力P和末端混合气温度T对于爆震预测必不可少,后文在实验和仿真的基础上分别评价了单一爆震预测模型和基于3-Arrhenius公式的混合爆震预测模型对煤油发动机爆震起始角的预测性能,从而得到点燃式航空煤油活塞发动机最佳的爆震预测模型。
2 试验系统及爆震评价指标
2.1 发动机试验系统搭建
试验所用发动机为德国LIMBACH公司生产的两缸、水平对置、二冲程、风冷发动机,其具体参数见表2。试验设备主要包括CWAC型交流电力测功机、Kistler 6113A火花塞式压力传感器、DH5960动态信号采集仪和ALM-ADV型空燃比分析仪等。试验所用燃料为RP-3航空煤油,喷射方式为进气道电喷,试验过程中喷油压力维持在0.3 MPa,进气温度为22~26 ℃。缸内压力采样频率为200 kHz,保证气缸压力数据采集分辨率为 0.1°CA,每个工况点至少采集300个循环。
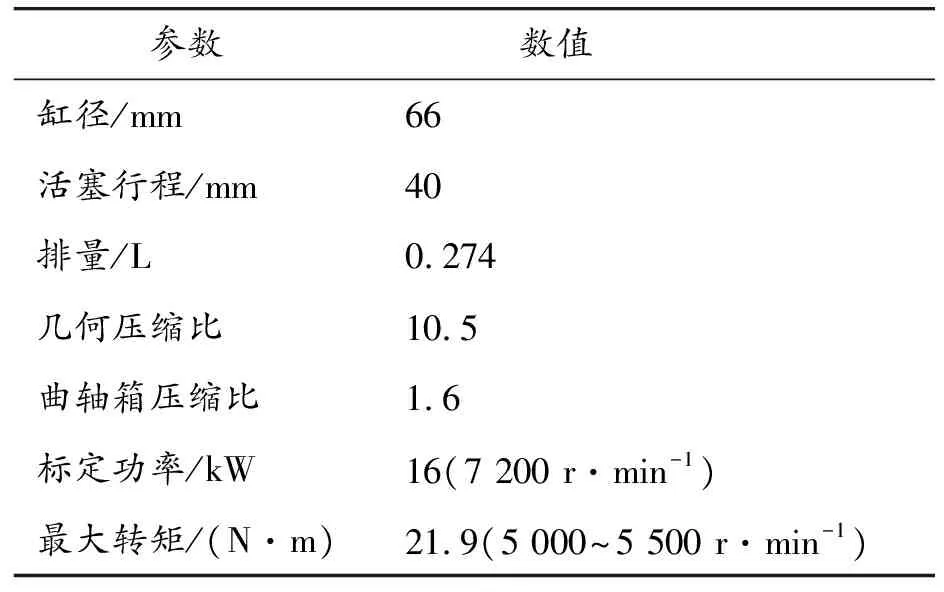
表2 发动机技术参数
本次发动机试验包含稳态工况和爆震工况,分别记录了发动机稳定运行时和发生爆震时的功率、燃油消耗率和气缸压力等数据,其中稳态工况下的试验数据将用于发动机一维性能仿真模型的标定。发动机稳态工况的转速为4 800~6 600 r/min、节气门开度为48%~100%,共计27个工况点。由于爆震对发动机的危害极大,且在此发动机的试验过程中发现转速为4 800 r/min、节气门开度为50%时,监测的气缸压力信号会出现轻微的振荡,据此判断发动机在该工况下易发生爆震。因此,为减小爆震对发动机的危害,爆震工况仅选择转速为4 800 r/min、节气门开度为50%,试验过程中只扫描点火提前角,使其从31°CA BTDC以1°CA的幅度不断增加至36°CA BTDC。采集了发动机每个循环的缸内压力变化。图2为发动机试验台架。

图2 发动机试验台架
2.2 试验数据处理
发动机缸内燃烧的不稳定性导致运行过程中每个循环的燃烧压力、燃烧放热率等指标存在差异。有研究表明二冲程火花点火发动机燃用航空煤油后其指示平均有效压力的循环变动率比燃用汽油时更高[23]。因此,为了获得模型标定所需的有效数据,提取了每个工况点下连续300个压力循环,并求得平均缸内压力。图3为发动机转速在6 200 r/min、92%节气门开度下的平均气缸压力处理结果,通过对每度曲轴转角对应的不同循环缸压求取平均值,获得了该工况下的平均缸内压力曲线。
爆震测量的方法有多种,而直接可靠的信号源只有爆震发生时燃烧室内的压力振荡,爆震时振荡的典型频率为5~10 kHz[24]。为了尽可能过滤正常燃烧时的低频缸压振荡以及高频的燃烧噪声,保留有效的爆震信号,本文使用带通滤波处理气缸压力信号来获取爆震评价指标,带通滤波的频率范围为3~25 kHz,可以覆盖到爆震时压力振荡的典型频率。取滤波后的最大压力振荡幅值(maximum amplitude of pressure oscillation,MAPO)作为爆震强度的评价指标,以此来区分爆震循环和非爆震循环[6-7]。图4为发生爆震时缸内压力的变化及带通滤波的处理结果。根据试验数据,采用文献[6]中所述方法,对临界爆震循环进行统计分析,最终确定爆震循环MAPO的阈值为0.08 MPa。图5为点火提前角从31°CA BTDC增大到36°CA BTDC时900个循环的MAPO统计结果,纵坐标为不同MAPO出现的频率,筛选获得了405个循环的爆震缸压。
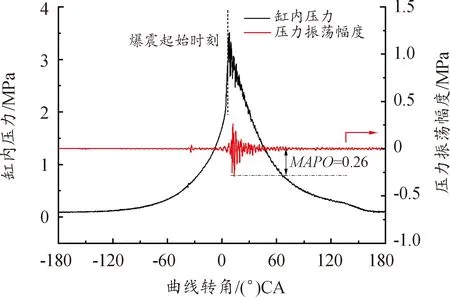
图4 爆震工况下缸内压力变化及压力振荡幅度

图5 不同MAPO的统计结果
获得准确爆震起始角(knock onset,KO)是验证爆震预测模型的前提。根据爆震机理,发动机发生爆震燃烧时缸内压力会出现突变,因此采用缸内压力曲线上第一个瞬间凸起对应的曲轴转角作为爆震起始角。
利用Matlab读取发生爆震时的缸压数据,通过ginput函数获得了气缸压力突变时刻所对应的曲轴转角。图6为逐渐增大点火提前角时连续200个循环的爆震起始角的统计结果。随着点火提前角的增大,缸内最大爆发压力所对应的曲轴转角提前,导致爆震起始时刻逐渐提早,由于发动机燃用煤油后循环变动率相比于燃用汽油时更高[23],使得测得的爆震起始时刻存在较大波动。
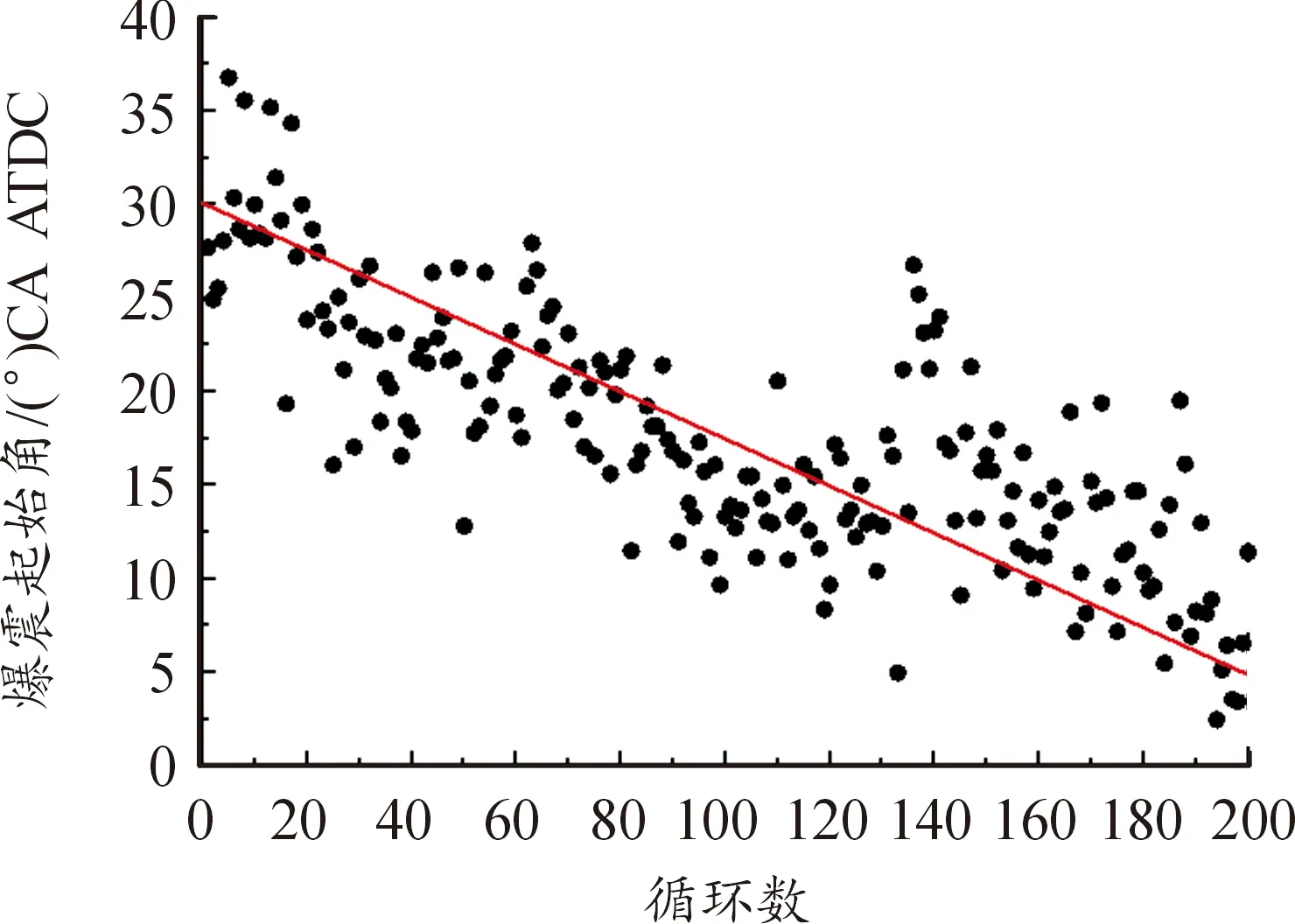
图6 连续200个循环的爆震起始角
3 末端混合气温度获取
决定爆震发生时刻的着火延迟期与末端混合气的压力和温度有关,气缸内压力随曲轴转角的变化可以通过实验获得,但是末端混合气的温度很难通过实验获得,普遍采用的方法是基于末端混合气绝热压缩求解得到[7]。定义进气口关闭时刻的缸内温度为初始温度,在绝热压缩条件下,可由式(8)计算得出末端混合气温度。
(8)
式中:T2为末端混合气温度;T1为初始温度;p1为进气口关闭时刻的气缸压力;p2为随曲轴转角变化的气缸压力;γ为混合气的比热比;其中p1和p2均由实验获得。
由于初始温度受到缸体换热以及燃油混合的影响,导致其与实测的进气温度并不相等,因此,为了获得较为准确的初始温度,需要建立该发动机的一维性能仿真模型。根据实验发动机的工作原理和结构尺寸,利用GT-Power对发动机的进排气系统、曲柄连杆等结构进行了建模,发动机的一维仿真模型如图7所示。
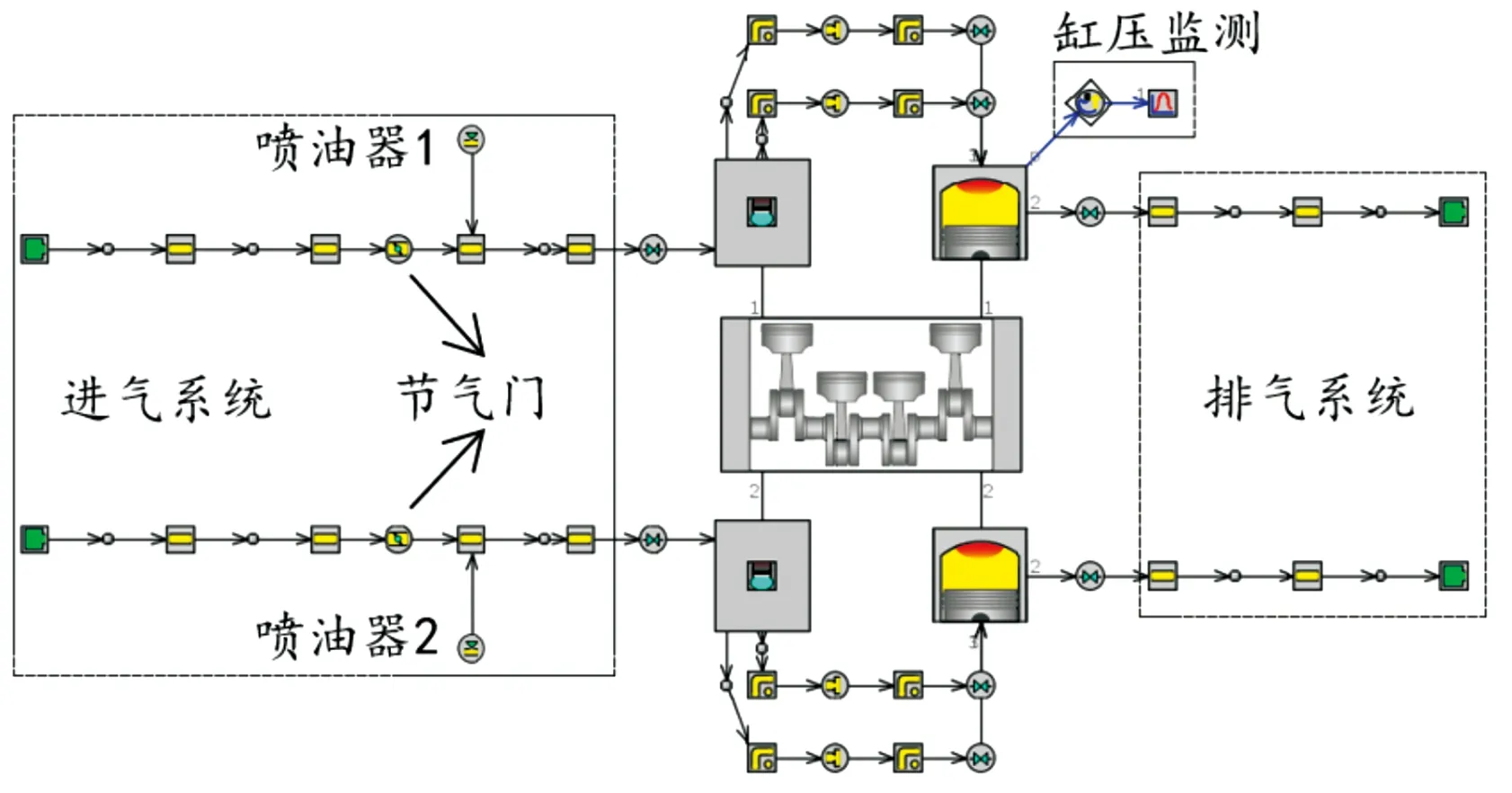
图7 发动机一维仿真模型
一维仿真模型中,传热和燃烧模型会显著影响初始温度的计算,本文选用普遍用于发动机数值模拟中的WoschniGT传热模型[25],该模型具有良好的计算精度。燃烧模型选用火花点火湍流燃烧模型(SI turbulent flame combustion model),然而软件中并没有关于航空煤油的模型参数。因此本文基于文献[16]中RP-3航空煤油燃烧试验数据计算获得了煤油的层流火焰衰减速度、温度指数以及压力指数等信息,应用于GT-Power燃烧模型参数的设置,通过实验数据对整个模型进行了校核,最终获得较为准确的初始温度,并利用式(8)计算得出末端混合气温度。
3.1 燃烧模型参数的获取及校核
层流火焰传播模型的参数需要通过计算获得,不同燃料的层流火焰传播速度也不尽相同,因此模型参数与燃料的种类有很大的关系。球形扩散火焰是火焰传播模型的基本假设,为了得到层流火焰传播速度随压力、温度变化的明确表达式,常用的方法是将实测的层流燃烧速度拟合为压力和温度的指数关系[26-27],如式(9)所示。
(9)
式中:Sl为层流火焰传播速度;S0为参考压力温度下的层流火焰传播速度;T为混合气温度;P为压力;T0为参考温度;P0为参考压力;α为温度指数;β为压力指数。
煤油的燃烧实验表明式(9)中的层流火焰传播速度由过量空气系数φ、混合气温度T以及压力P决定,方程系数α和β根据试验测得的RP-3航空煤油燃烧数据计算得到,图8为文献[16]中不同温度压力下层流火焰传播速度与过量空气系数之间的关系。
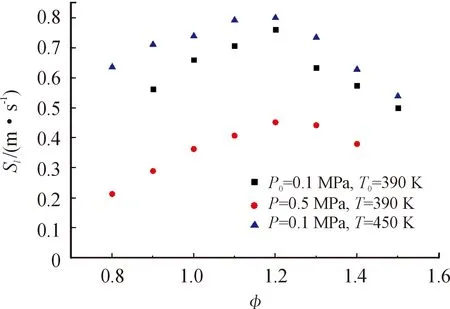
图8 不同温度压力下层流火焰传播速度随过量空气系数的变化
据此可计算出温度指数α和压力指数β随过量空气系数φ的变化关系,结果如表3所示。

表3 温度指数和压力指数
GT-Power的燃烧模型对式(9)进行了部分修正,考虑了实际工程中可能会应用的废气再循环技术,同时将S0替换为与过量空气系数相关的函数,其层流火焰传播速度SL表示为
(10)
式中:Bm为参考温度和参考压力下的最大层流火焰传播速度;φm为最大层流火焰传播速度对应的当量比;Bφ为层流火焰衰减速度;φ为过量空气系数;fEGR为废气再循环率的函数。由于暂不考虑废气再循环技术,此时fEGR为1。根据系数定义和试验数据可知φm为1.2,Bm为0.761 m/s,为方便计算,Bφ取不同压力温度下层流火焰衰减速度的平均值,即-0.701 m/s。
实际的燃烧过程非常复杂,有规律可循的层流火焰传播只是其一部分,在火焰传播中湍流的影响也不可忽视[28]。湍流与详细化学反应机理之间存在强烈的非线性相互作用,且湍流运动具有无序性和随机性,目前尚未有普遍适用的湍流火焰传播模型。
为方便建立不同发动机的湍流火焰传播模型,需要在GT-Power软件内设置3个湍流火焰传播的模型参数,分别为火核生长速度因子FKG(flame kernel growth multiplier),湍流火焰速度因子TFS(turbulent flame speed multiplier),泰勒微尺度缩放因子TLS(Taylor length scale multiplier)。3个参数的默认值均为1,对于不同发动机存在一组最合适的参数值,因此需要根据发动机稳态工况下的试验数据优化这3个参数。本文利用GT-Power软件内置的参数优化板块DOE(design of experiments)对这3个模型参数进行优化,根据GT-Power使用手册,选择参数优化范围为0.5~3.0,选择拉丁超立方(Latin hypercube sampling)的采样方法,分别对这3个参数在优化范围内取值,得到了1 000种模型参数的组合方式。随后对这1 000个样本进行试算,以发动机稳态工况下的功率、燃油消耗率和缸内压力作为参数优化依据,筛选出仿真值与实验值误差最小的样本。图9为转速在4 800 r/min、节气门开度为82%时针对功率的参数优化结果。对筛选出的213个样本依次进行针对燃油消耗率和缸内压力的参数优化,得到一组此工况下发动机湍流火焰传播的模型参数。
使用上述方法对该发动机的其他工况点进行模型参数优化,最终获得发动机全工况下完整的一维仿真模型。图10为转速在4 800、5 200、5 600和6 200 r/min时不同节气门开度的实验功率和仿真功率对比,两者误差在5%以内。图11为转速在4 800 r/min、不同节气门开度下实验的燃油消耗率与仿真的燃油消耗率对比,两者误差在8%之内。图12为转速在4 800 r/min、节气门开度为50%时,300个循环的实验平均缸压与仿真缸压的对比,两者误差在6%之内。
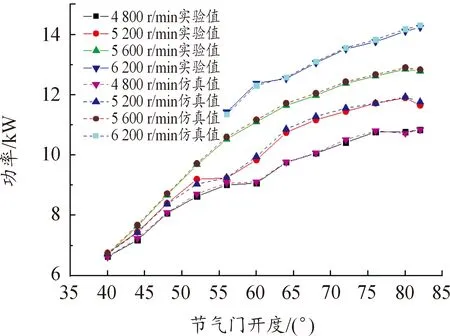
图10 不同节气门开度下的实验与仿真功率对比
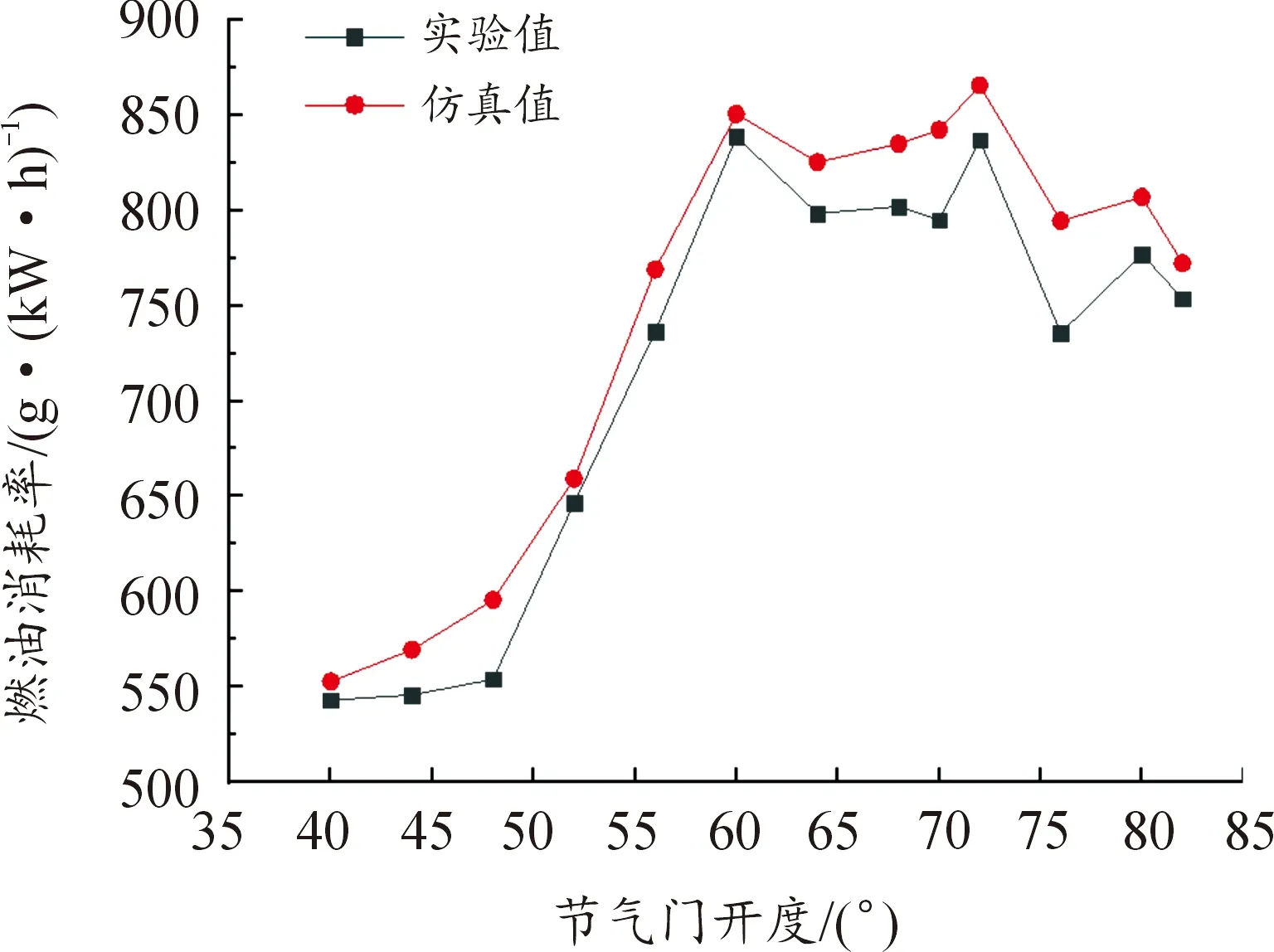
图11 实验与仿真燃油消耗率对比
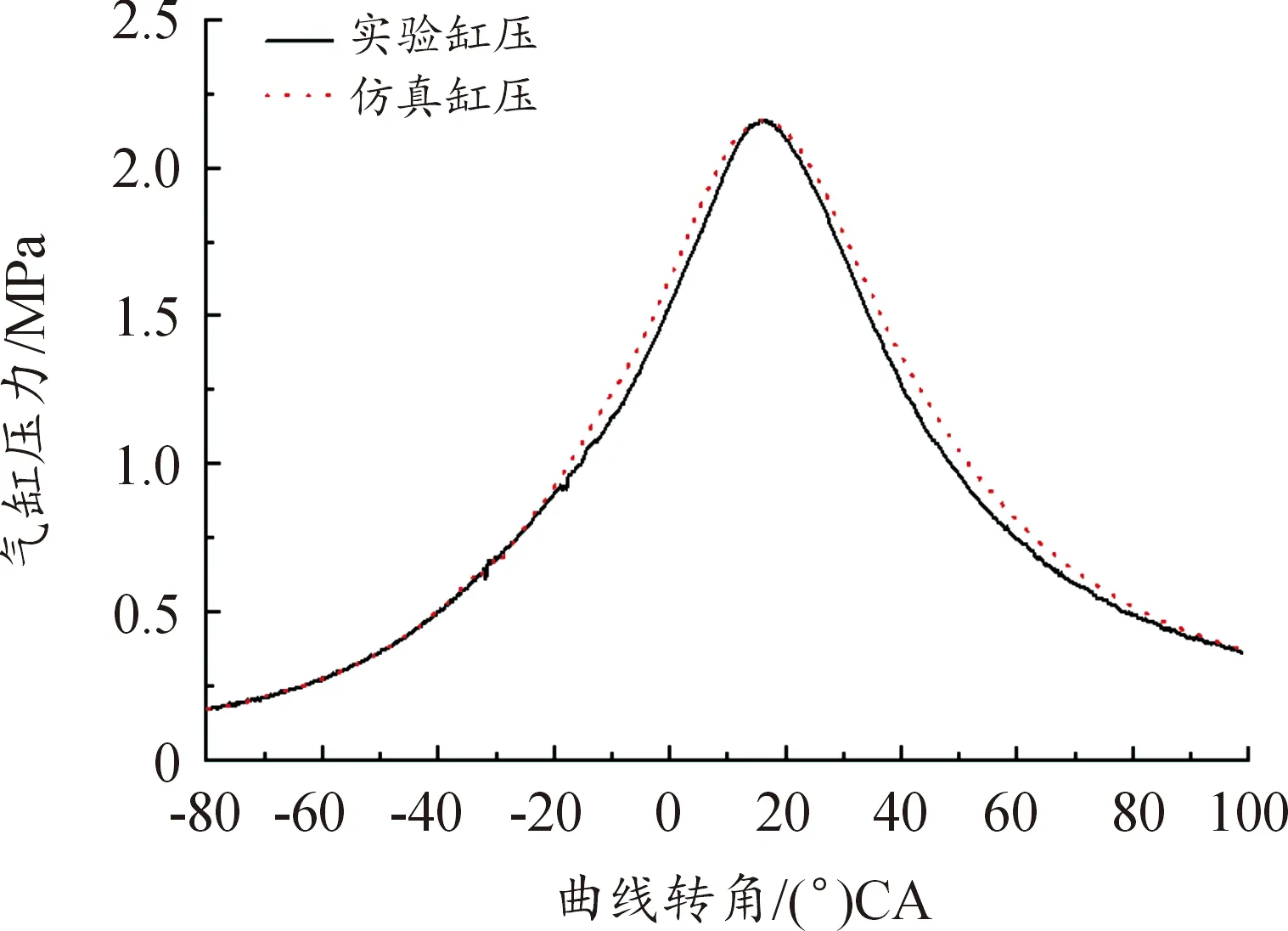
图12 实验与仿真缸压对比
3.2 计算末端混合气温度
通过对上节燃烧模型参数的计算和校核,得到了该发动机完整的一维仿真模型,可以较为准确地计算进气结束时刻的缸内温度。为了计算末端混合气温度,还需确定混合气的比热比。根据文献[7]可知,混合气的温度、组分以及各组分所占的比例均会影响混合气的比热比,随着过量空气系数的减小,混合气的比热比会随之减小,而随着温度的升高混合气的比热比也有减小趋势,当发动机活塞上下运动时,气缸内的温度和组分会有较大的改变。因此采用定比热比计算末端混合气温度会产生很大的计算误差,而末端混合气温度会直接影响到着火延迟积分的计算结果,从而影响爆震预测的精度。
本文采用校核后的一维仿真模型计算出比热比随曲轴转角的变化关系,通过式(8)计算每个循环的末端混合气温度。图13为4 800 r/min、节气门开度为50%时,某一循环采用变比热比计算末端混合气温度的计算结果。
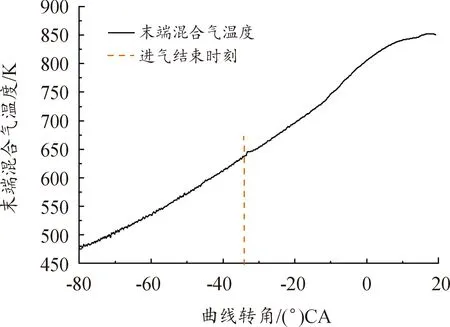
图13 某一循环末端混合气的计算结果
4 爆震预测模型的性能评估
为了定量分析单一Arrhenius形式的爆震预测模型与本文提出的基于3-Arrhenius公式的混合爆震预测模型对爆震起始时刻预测的准确性,使用Matlab输入温度、压力和2种模型的表达式等数据,找出了着火延迟积分恰好等于1的时刻,并将其换算为对应的曲轴转角记为预测的爆震起始角(predicted knock onset,PKO),然后对比PKO与试验的爆震起始角(experimental knock onset,EKO)之间的误差即可评估爆震预测模型的性能。
图14为单一爆震预测模型和混合爆震预测模型对同一轻微爆震循环的预测结果。当着火延迟积分等于1时,对应的曲轴转角即为预测的爆震起始角。由图14(a)可以看出,单一爆震预测模型对着火初期的低压区很敏感,着火延迟积分在发生爆震之前就快速增加,不能识别爆震发生时缸内压力的突然升高,导致预测的爆震起始角略小于实际的爆震起始角。由14(b)可以看出,混合爆震预测模型能够识别着火初期的低压区。当缸内压力因着火而快速升高时,着火延迟积分也随之快速增大,从而能够对爆震发生时缸内压力的突然升高做出反应,预测的爆震发生时刻更加接近实际的爆震发生时刻。

图14 不同爆震预测模型对同一轻微爆震循环的预测结果
图15为单一爆震预测模型和混合爆震预测模型对同一严重爆震循环的预测结果。
严重爆震时缸内压力会突然升高同时伴随着高频的振荡,而单一爆震预测模型不能很好地对缸内压力的突然升高做出反应,导致预测的爆震起始角滞后于实际的爆震起始角。混合爆震预测模型在这方面表现出了更好的预测性能,当压力因爆震而突然升高时,着火延迟积分也随之快速增大,最终预测的爆震起始角更加接近实际的爆震起始角。
基于3-Arrhenius公式的混合爆震预测模型对于轻微爆震和严重爆震都具有良好的预测性能,混合爆震预测模型能够区分正常燃烧与爆震燃烧的气缸压力变化。图16为单一爆震预测模型和混合爆震预测模型对所有爆震循环的预测结果,2个模型预测的爆震起始角与实际的爆震起始角之间的标准误差分别为3.23°CA和1.19°CA。
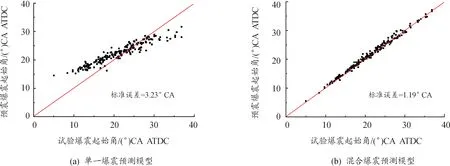
图16 不同爆震预测模型对所有爆震循环的预测结果
5 结论
1) 根据正庚烷和甲苯的着火延迟模型参数,提出了基于3-Arrhenius公式的航空煤油两组分混合着火延迟时间计算式。
2) 采用已公开的航空煤油燃烧数据,在GT-Power软件平台上搭建了煤油的燃烧模型,并根据发动机实验数据对该燃烧模型进行了验证。
3) 混合爆震预测模型的PKO与EKO之间的标准误差为1.19°CA,而单一爆震预测模型的PKO与EKO之间的标准误差为3.23°CA,混合爆震预测模型更加符合真实燃料的燃烧过程,表现出了更好的预测性能。
