采用自适应遗忘因子的永磁同步电机预测电流控制

龙 涛,刘蕴博,常九健

(1.合肥工业大学 汽车与交通工程学院, 合肥 230009;2.合肥工业大学 汽车工程技术研究院, 合肥 230009)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)具有高效率、高功率密度、高转矩电流比、宽调速范围等优势,得到了广泛应用[1]。在PMSM本体结构不断优化更新的同时,PMSM控制技术也得到了快速发展,目前研究比较成熟且应用广泛的是基于磁场定向的矢量控制策略(field oriented control,FOC),FOC是通过坐标变换实现对定子电流励磁分量和转矩分量的独立控制,从而完成对转矩和磁链的解耦过程。FOC是基于比例积分(proportional integral,PI)控制器在多环级联结构中实现的,具有较好的稳态性能。但是由于PI控制器存在积分饱和现象,并且在控制过程中无法考虑电流幅值和电压幅值等约束条件,已不能满足所要求的良好的动态响应能力。在电机的其他控制方法中,模型预测控制具有控制结构简单、动态响应快、易于实现多目标协同控制、易于处理系统约束条件等优点,受到了国内外学者的广泛关注与研究[2-3]。其中有限状态集(finite-control-set MPC,FCS-MPC)模型预测控制技术基于系统预测模型,通过遍历逆变器的所有开关状态对应的电压矢量,以及预测模型计算出预测值,代入表示控制目标以及约束条件的代价函数进行评估,得到最优控制矢量用于下一个周期的控制驱动[4-5]。FCS-MPC由于操作简单,原理简洁直观,且不需要调制模块,从而具有更好的动态响应性能,是电机控制领域的热点。

然而FCS-MPC控制策略仍有一些问题,有限集模型预测控制在一个控制周期内只采用一种电压矢量,影响控制精度,为了提高控制性能,通常要求较高的采样频率[6-7]。由于FCS-MPC是基于系统的数学模型实现的,所以控制性能高度依赖于控制模型参数的准确性,由于测量精度等问题,电机的参数值难以准确获取,并且实际运行过程中,电机参数会随着运行工况发生变化,如电阻和磁链会受温度的变化而变化,温度升高时,电阻会增大,磁链会降低。电感会受到磁链饱和的影响,电流又是导致磁链饱和的重要原因。当电机运行在负载变化的工况时,电机电流的变化最终会导致电机的电感参数发生变化。这种参数变化的现象会造成预测控制模型与电机实际模型的参数失配,从而导致控制系统的控制效果下降,随着参数失配的程度越大,控制效果越差。

针对这种问题,国内外学者展开了众多研究,有研究表明可以采用设计观测器的方法实现扰动观测补偿[8-9],通过观测器可以将影响控制性能的众多因素,如参数失配、外部扰动、测量误差、逆变器非线性带来的影响统一视为一个总的扰动,通过观测器估计扰动的数值并在控制过程中进行前馈补偿,但是由于观测器的使用加上引入相关参数的调节等问题,会增加算法的复杂程度,进而影响其动态响应性能。

除此之外,可以通过将本周期的实际采样值与上一周期预测得到的电流预测值做差,得到预测误差,将预测误差用于下一周期的电流预测中对其进行补偿[10],然而前一周期的电流误差值是在其特定的电压矢量时产生的,与其余矢量没有直接关系,这样直接用在下一周期的预测中会严重影响控制效果。另有文章采用了无模型MPC,此方法不需要通过数学模型进行预测,而是直接对不同电压矢量对应的电流变化率进行电流预测,无需依赖电机的具体参数,但是该方法要求很高的采样精度,并且预测过程中存在着明显的滞后现象[11]。文献[12]提出了一种比例-积分-微分型代价函数,但是该方法仅在参数变化范围较大的情况能起到降低误差的效果,并且代价函数的复杂化直接影响到每一次采样时的计算时间,进而影响控制性能。还可以用参数辨识的方法实时辨识变化的电机参数值,目前参数辨识的研究多用于永磁同步电机的矢量控制中,常见的有递推最小二乘法[13-14]、扩展卡尔曼滤波法[15-16]、模型参考自适应法[17],其中递推最小二乘法由于结构简单、计算量小、识别精度高、收敛速度快等优点,在PMSM参数辨识中得到广泛应用。Xun等[18]将带遗忘因子的最小二乘法应用到永磁同步电机的参数辨识中,提高了辨识算法的动态性能。在基于遗忘因子的最小二乘法参数辨识过程中,大多将遗忘因子设成恒定值,当设置较小的遗忘因子值时,可以提高算法的收敛速度,与此同时也会降低算法的稳定性,当设置成较大的遗忘因子值时得到的结果和较小值相反。这样就会面临一个动态性能和稳定性能的取舍的矛盾问题。

针对上述问题,本文设计一种基于自适应遗传因子的递推最小二乘法参数辨识,在辨识过程中,根据当前时刻的实际采样值与上一个时刻辨识结果的理论值做差,根据差值建立自适应遗忘因子动态函数,实时计算遗忘因子的取值,实现了遗忘因子的自适应选择,解决了收敛速度与稳定性的取舍矛盾问题,提高模型预测控制算法的综合性能。

1 有限集模型预测电流控制

1.1 永磁同步电机数学模型

本文采用内嵌式永磁同步电机(interior permanent magnet synchronous motor,IPMSM)进行分析,对三相静止坐标系下的IPMSM数学模型经过坐标变换可以得到d、q轴两相同步速旋转坐标系下IPMSM的电压方程:

(1)

式中:Ud、Uq为分别为d、q轴定子电压;Rs为定子电阻;id,iq为d、q轴定子电流;Ld、Lq分别为d、q轴电感;ωe为转子电角速度;ψf为永磁体磁链;Ud、Uq由α、β坐标系下Uα、Uβ经过Park变化计算得到,即

(2)

式中:θ为电角度。本文研究的PMSM控制方法基于三相两电平电压源逆变器实现,其结构如图1所示。其中8种开关状态对应8个电压矢量(U0、U1、U2、U3、U4、U5、U6、U7),如图2所示,Uα、Uβ可根据逆变器开关状态Sabc,见表1,表1中Udc为直流母线电压。

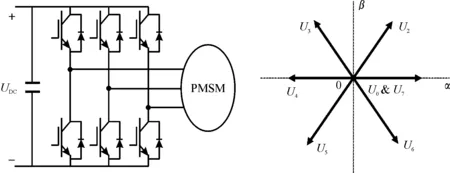
图1 电压源逆变器结构示意图 图2 和开关状态对应的电压矢量图

表1 开关状态

1.2 永磁同步电机预测控制模型

算法在DSP等微处理器上运行,所以本文采用前向欧拉法[19]对式(1)在k时刻离散化,得到预测模型为:

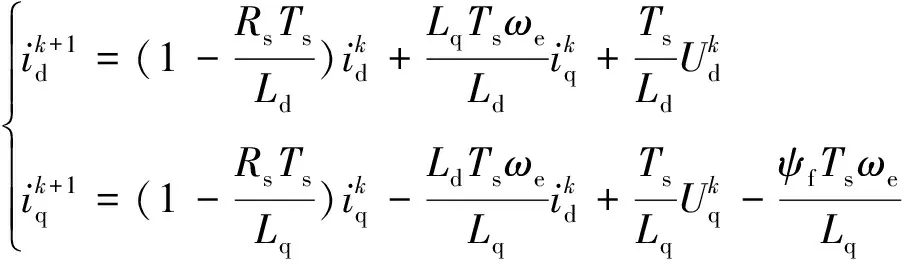
(3)

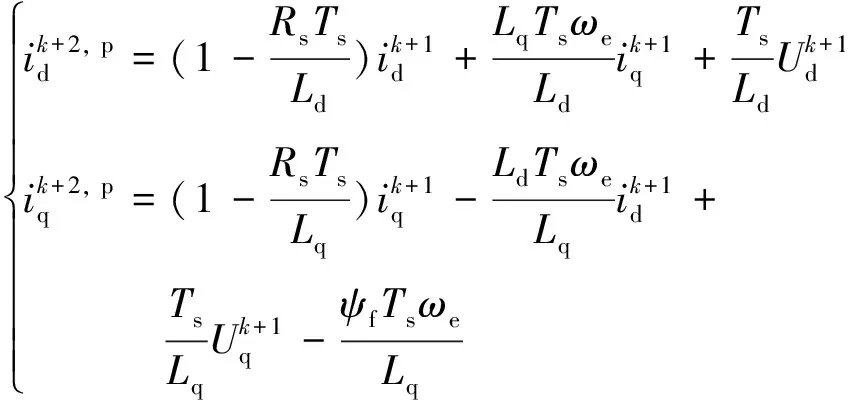
(4)

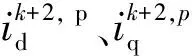
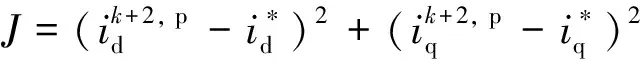
(5)

由上述分析可知,控制算法在整个预测过程中都依赖于电机的数学模型,其中电机参数准确与控制系统的综合性能起着至关重要的作用,因此保证预测控制数学模型与电机实际的参数匹配具有重要意义。

2 基于参数补偿模型预测电流控制

针对运行过程中电机参数变化导致因参数失配影响控制性能的问题,本节将具体阐述如何用基于自适应遗忘因子最小二乘法的方法对电机参数进行实时辨识,首先介绍传统的最小二乘法。

2.1 传统最小二乘法

最小二乘法算法的基本模型如下

y(k)=φT(k)θ(k)+e(k)

(6)

式中:θ为参数向量集;φT(k)为输入矢量;y(k)为输出量;e(k)为噪声向量。输入量和输出量在算法运行过程中都可以通过测量得到,将测量值代入到代价函数g(θ)中,使代价函数最小进而修正参数向量集。代价函数g(θ)公式为:

ε(θ)=y(k)-φT(k)θ(k)

g(θ)=ε(θ)Tε(θ)

(7)

L(k)=P(k-1)φ(k)[I+φT(k)P(k-1)φ(k)]-1

θ(k)p=θ(k-1)p+L(k)[y(k)-φT(k)θ(k-1)p]

P(k)=[I-L(k)φT(k)]P(k-1)

(8)

式中:θ(k)p、θ(k-1)p参数向量预测值,也就是所要辨识的参数;P(k)为协方差矩阵;L(k)为增益矩阵;I为单位矩阵。

本文对预测精度影响较大的2参数值Ld,Lq进行辨识,令电阻Rs与ψf为常量。对比电机模型可知,该辨识算法在永磁同步电机中应用时各变量如下:

(9)

其中,随着递推次数的递增,P(k)会越来越小,采样新值对辨识的影响越来越小,即数据饱和现象,导致收敛的速度变慢,为了提高收敛速度,对过去的数据乘上权重因子λ,人为降低旧数据的作用,加入权重因子后,算法的公式为:

L(k)=P(k-1)φ(k)[λ·I+φT(k)P(k-1)φ(k)]-1,

θ(k)p=θ(k-1)p+L(k)[y(k)-φT(k)θ(k-1)p]

P(k)=[I-L(k)φT(k)]P(k-1)/λ

(10)

λ又被称为遗忘因子,所以算法又被称为基于遗忘因子的递推最小二乘法,当λ=1时,算法就是传统的递推最小二乘法。

2.2 基于自适应遗忘因子的最小二乘法参数辨识

遗忘因子可以人为降低旧数据的作用,λ通常取0.95～1之间,λ值取小可以起到提高收敛速度的作用,但是该值太小又会导致在参数辨识过程中出现过大的噪声,影响辨识结果的稳定性,而λ通常是一个固定值,这就会造成收敛速度与稳定性的取舍的矛盾问题,针对此问题,本文提出一种自适应遗忘因子的最小二乘法参数辨识,可在辨识过程中同时保证稳定性与动态性能。

根据当前时刻的实际采样值与上一个时刻辨识结果的理论值做差,根据差值建立自适应遗忘因子动态函数,实时计算遗忘因子的取值,实现了遗忘因子的自适应选择。实际采样值与上一个时刻辨识结果的理论值做的差值η(k)为:

η(k)=(y(k)-φT(k)θ(k-1)P)2

(11)

式中:η(k)表示辨识过程中变化情况,当η(k)较大时,证明正在辨识的参数变化较快,因为此时辨识算法的首要任务是提高算法的收敛速度,所以要采用较小的遗忘因子λ。当η(k)较小时,证明辨识的参数逐渐趋于稳定,因为此时辨识算法的首要任务是尽量减少噪声带来的影响,得到稳定且精度高的辨识结果,所以要采用较大的遗忘因子λ。

经过上述分析,本文可以提出自适应遗忘因子λ(k)的函数为:

(12)

式中:参数1为设置的遗忘因子的上限;α为设置的遗忘因子的下限;β为可调参数;因为η(k)为二阶矩阵且各变量变化一致,所以选择其中一阶参数τ(k)进行计算。将自适应遗忘因子函数代入递推最小二乘法,得到最终优化后的算法公式为:

L(k)=P(k-1)φ(k)[λ(k)·I+φT(k)P(k-1)φ(k)]-1

θ(k)p=θ(k-1)p+L(k)[y(k)-φT(k)θ(k-1)p]

P(k)=[I-L(k)φT(k)]P(k-1)/λ(k)

(13)

经过上式迭代计算后的θ(k)p,即为最小二乘法参数辨识得到的电感值,利用辨识结果对预测控制数学模型进行参数更新,保证预测控制数学模型的参数与电机实际的参数匹配,从而提高模型预测控制算法的控制性能。

3 仿真分析与讨论

为验证基于自适应遗忘因子参数辨识的情况以及预测电流控制的综合性能,在Matlab/Simulink仿真环境中进行验证,仿真所用的永磁同步电机参数见表2。

表2 电机参数

3.1 自适应遗忘因子参数辨识分析

为了研究参数变化时会对参数辨识产生何种影响,采用电机的数学模型进行仿真,此方法可以给电机阶跃的参数变化。因为电感受到磁链饱和的影响发生变化且d轴电感和永磁体磁链处于同一方向,所以d轴磁链本身处于比较饱和的状态,d轴电流变化时,d轴电感变化相对较小;而q轴磁链则完全由q轴电流产生,因此,q轴电感随着电流的变化发生大幅度变化。所以在仿真过程中,以q轴电感为例进行分析,设置递推最小二乘法参数辨识协方差矩阵初值P(0)=eye(3)×10-4,参数向量集初值θ(0)=[0.000 1 0.000 1 0]T,设置仿真采样周期为0.1 ms,仿真时间为2 s,令永磁同步电机q轴电感在1 s时降低30%,即Lq由0.425 mH下降到0.3 mH。本文提出的基于自适应遗忘因子的最小二乘法参数辨识的自适应遗忘因子λ(k)由(12)式取值。α为辨识算法的下限值,本文取0.95。β为可调参数,经过大量仿真得知,当β取0.7时,可得较好的辨识结果。分别对遗忘因子λ=0.950、λ=0.999以及λ=λ(k)进行对比仿真分析,参数辨识的仿真结果如图3所示。

由图3可知,当λ=0.999时,递推最小二乘法参数辨识的稳定性较好,不易受到噪声干扰,但是辨识算法收敛的速度慢。当λ=0.950时,递推最小二乘法参数辨识的动态性能有很大改善,但在辨识过程中出现了很大的波动,稳态性能变差。当λ=λ(k)时的辨识算法在辨识过程中具有快速的收敛性,并且能够稳定地跟随电机参数的变化。

图3 λ=0.99和λ=0.95以及λ=λ(k)时Lq辨识情况

通过对比不同算法之间的上升时间tr以及在0.5～1 s稳定时辨识结果的方差D,可以定量分析不同算法间的动态性能和稳态性能,结果如表3所示。

表3 不同遗忘因子时的结果

由表3可知,λ=λ(k)时的上升时间tr小于λ=0.999时的上升时间,并且稳定时的方差小于λ=0.950时的算法。由数据分析可知,基于变遗忘因子的算法相比于遗忘因子为固定值的算法,在辨识时具有不错的动态性能和稳态性能。

3.2 基于参数辨识时模型预测控制性能验证

针对电机参数变化导致因参数失配的问题,本文采用参数辨识的方法实时辨识电机参数,修正控制预测模型,为体现控制性能的优化程度,在Matlab/Simulink仿真环境中进行验证,仿真所用的永磁同步电机参数见表1所列。采用电机的数学模型进行仿真,为了仿真变载时电感变化的工况,令永磁同步电机q轴电感在1 s时降低30%,设置仿真采样周期为0.01 ms,仿真时间为2 s,令电机运行于200 r/min,负载转矩为50 N·m。为分析电感参数变化对控制性能的影响,对传统模型预测电流控制与利用参数辨识算法优化后的模型预测电流控制进行对比仿真。Lq变化时对q轴电流Iq,转矩Te,d轴电流Id的影响仿真如图4所示。

图4 有无参数辨识算法时的仿真图

当Lq变化后,q轴电流Iq,转矩Te,d轴电流Id的方差如表4所示。

表4 有无参数辨识时的方差

从图4中可以看出,在0～1 s电感未发生变化时,无参数辨识算法与有参数辨识算法的仿真效果一致。当q轴电感发生变化时,从图4(a)和图4(b)可以看出,无参数辨识算法中,q轴电流和转矩都产生了较大的脉动,从图4(c)可以看出,Lq的变化对d轴电流影响不明显。由表4可以看出,在Lq变化时,优化后算法q轴电流和转矩的方差小于未优化时的方差。d轴电流的方差无明显变化。在q轴电感降低30%时,无参数辨识MPC算法中的Iq和Te的波动比有参数辨识后的Iq和Te的波动大43.6%。由此得知无参数辨识MPC算法的控制效果明显下降。

令永磁同步电机仍运行在相同工况下,对普通的λ为0.999的最小二乘法参数辨识与基于自适应遗忘因子的最小二乘法参数辨识进行对比仿真。Lq变化时对q轴电流Iq,转矩Te,d轴电流Id的影响仿真如图5所示。

图5 不同参数辨识算法时的仿真图

由图3分析可知,当Lq变化时,基于自适应遗忘因子的算法比λ为0.999固定值的普通参数辨识算法具有更好的动态性能。因此取1～1.3 s内的q轴电流Iq,转矩Te,d轴电流Id的方差如表5所示。

表5 基于自适应遗忘因子与普通辨识算法的方差

从图5可以看出,在1～1.3 s时,普通最小二乘法参数辨识的q轴电流和转矩都产生了较为明显的脉动。由表5可以看出,基于自适应遗忘因子的算法的q轴电流和转矩的方差小于普通的最小二乘法参数辨识的方差。d轴电流的方差无明显变化,由(4)式可知,当算法计算步长很小时,q轴电感对d轴电流的影响比重不大。同理可知,永磁体磁链ψf,与电阻Rs对电流预测时的比重很小。又因为d轴电感变化相对较小,故本文只分析q轴电感变化。

综上所述,图4的仿真和表4说明当电感变化时,没有参数辨识的MPC算法由于预测模型参数不匹配导致控制效果变差。参数辨识可以抑制因电感变化而导致的电流,转矩脉动增大的现象,稳态性能明显好于无参数辨识的算法。另一方面,图5的仿真和表5说明,本文提出的基于自适应遗忘因子的参数辨识算法相较于普通的参数辨识算法,在参数突变的一段时间内,电流、转矩脉动低于普通的最小二乘法参数辨识算法,具有更好的控制效果。

4 结论

针对永磁同步电机模型预测控制在电机模型参数失配时影响控制性能的问题,提出一种基于自适应遗忘因子的最小二乘法参数辨识方法,使用基于模型预测算法的电机模型对参数辨识时的动态以及稳态性能进行仿真分析,并且对有无参数辨识的模型预测算法以及基于自适应遗忘因子的参数辨识算法和普通的参数辨识算法分别进行对比分析。仿真结果显示,基于参数辨识的模型预测算法对电感变化具有一定的抗干扰性。基于自适应遗忘因子的最小二乘法参数辨识在辨识过程中具有快速收敛性且能够稳定地跟随电机参数的变化,相较于一般最小二乘法参数辨识算法,具有更好的控制效果。