基于层次聚类的桥梁模态参数自动识别及异常诊断

马新颖

(天津城建设计院有限公司,天津 300122)

桥梁运营模态参数一般通过分析健康监测系统加速度数据获得,大量长期的模态参数是评估桥梁-环境相关性和结构整体性能演化过程的重要基础[2]。传统桥梁监测的加速度数据的分析依靠商业模态分析软件,但是商业软件每次只能分析一次数据,得到一组模态参数。为了获得大量模态参数,模态参数自动识别方法逐渐得到重视,研究最多的是基于稳定图识别的模态参数自动识别[3-6]。

许多研究人员将聚类算法引入稳定图自动识别,如谱系聚类[5]、图论聚类[4]、模糊聚类和层次聚类[3]等,其中谱系聚类、图论聚类和层次聚类虽然从聚类方法属于不同的方法分支,但从识别过程上来说,具有相同的原理,都学要设定合适的阈值来实现聚类,而现有方法基本都采用固定阈值[5,6]。固定阈值通常基于经验获得,实际情况中,不同的结构需要不同的阈值,因此,固定阈值识别得到的模态参数通常不是很准确,要想得到精确的模态参数,必须寻求其它方法。

为解决现有模态参数识别结果的精度问题,本文提出基于两阶段层次聚类的模态参数自动识别及基于箱形图的异常值诊断方法。通过对原始层次聚类方法进行改进,分频率和振型两阶段分别进行聚类,识别稳定轴;然后将基于箱形图的异常值检测算法引入模态参数识别,检测稳定轴数据中的异常值,剔除异常值,得到精确的模态参数识别结果。

1 基本理论

1.1 层次聚类

层次聚类算法主要用在大数据分析和图像识别领域,层次聚类是基于某项指标对待分析数据按照相似性归类的过程,将小于指标的数人为具有相似性,归为一类,否则单独成一类。层次聚类首先假定数据集中的每一个数据都是一个小类,计算每个小类之间的距离,形成距离矩阵;然后将距离小于聚类指标的数据合并成一类,形成新类;最后再计算每个新类之间的距离,将距离小于聚类指标的类再合并成一类。按上述过程不断循环,直至所有类之间的距离大于聚类指标,则停止聚类,得到最终聚类结果。

为反应样本整体数据特性,本文采用每个类的平均值之间的间距作为类间距离。

1.2 基于箱形图的异常值检测

箱形图于1977年由美国著名统计学家约翰·图基首先提出,是一种用来显示数据分散情况的统计图,通过箱形图能够显示待统计数据的最大值、最小值、中位数、及上下四分位数,可以分析数据长期变化及多组数据的不同。箱形图的分位数的计算完全基于样本数据本身,不依赖任何数据特征的假设,因此箱形图的分位数能够反映样本本身的固有数据特征。

基于箱形图的异常检测指一组数据中小于Q1-1.5IQR或大于Q3+1.5IQR的值,其中Q1表示上四分位,Q3表示下四分位,IQR表示四分位间距。基于箱形图的异常值检测从已有数据的本身特性出发,不对样本数据进行任何分布假设,因此能够最合理的识别异常值。

基于箱形图的异常值检测方法相比于其他异常值检测方法具有更好的耐抗性,该方法以样本数据的四分位数和四分位距为指标,而四分位数具有较强的抗噪性,即使含噪样本有多个异常值也不会很大的扰动样本的四分位数,所以异常值不能对这个标准施加影响,箱形图识别异常值的结果比较客观。

2 基于两阶段层次聚类的模态参数自动识别及异常诊断

2.1 两阶段的层次聚类法

聚类过程实际上是具有相似特征的数据的归类过程,通过设定归类指标,将小于该指标的数据归为一类。

在稳定图理论中,稳定轴的基本判别指标是识别结果的连续性,在识别结果的所有物理指标中,频率的稳定性占首要位置。传统聚类算法将频率和MAC的聚类指标强行合并,容易将非稳定点识别为稳定点,由此造成识别结果不准确。

为了避免将非稳定点识别为稳定点,对传统聚类算法进行改进。首先基于层次聚类算法,以频率差为聚类指标,将频率稳定点进行聚类,识别频率稳定轴,并剔除稳定点较少的轴,频率稳定点较少说明在频率上不稳定,频率不稳定的点一定是虚假识别结果;然后,再次运用层次聚类法,以MAC值为聚类指标,将识别的频率稳定轴中的识别结果按MAC指标进行聚类,并剔除MAC稳定点较少的类,保留稳定点较大的类作为最终识别结果。

两阶段聚类过程分别在聚类的两个阶段将频率和MAC作为聚类参数指标,有效克服了传统聚类算法可能将非稳定点纳入稳定轴的缺点。

2.2 迭代的箱形图异常值诊断

稳定图中不同阶的稳定轴具有不同的数据离散特性,现有聚类算法(包括本文方法)都采用固定的聚类指标进行稳定轴识别,这种根据工程经验确定的聚类指标一般都偏大,导致识别结果中存在一些异常值。

为准确评估识别结果的合理性,剔除识别结果中的离散值,识别得到更准确的模态参数,引入基于箱形图异常值诊断方法的迭代的异常值剔除过程,通过对识别的稳定轴中的频率、MAC及阻尼比等指标进行异常检测,剔除异常识别结果,得到最终稳定轴识别结果。传统采用频率和MAC联合指标的聚类过程得到稳定轴后无法判别阻尼比等物理参数的合理性,因此很容易引入阻尼比异常的识别结果,提出的箱形图异常值检测方法能够检测识别结果中任何物理指标的合理性,保证识别结果的精确性。

基于箱形图的迭代的异常值诊断过程如下。

(1)首先计算识别结果中的某物理参数的箱形图分位值,并计算异常值诊断指标。

(2)然后,剔除位于箱形图之外的异常数据。

(3)最后,以剩余的识别结果为样本,重复(1)(2),直至没有异常值被检测出,停止计算。

2.3 基于两阶段层次聚类的模态参数自动识别及异常值诊断流程

通过对聚类过程的改进,并引入基于箱形图的异常值诊断过程,实现稳定轴自动精确识别。

3 工程实例

3.1 桥梁概况

桥梁为576.2+1418+481.8=2 476(m)的双塔三跨连续钢箱梁悬索桥,大桥建成之初便安装了健康监测系统,其中主梁共安装26个竖向传感器,上下游对称布置。本文采用2014年11月1日零时的监测数据进行分析,验证所提算法的合理性。

3.2 模态参数识别

基于SSI法识别模态参数,系统阶次设定为2～100。识别得到的所有模态参数如图1。从图1上虽然能够看到稳定轴,但也存在大量的非稳定点。

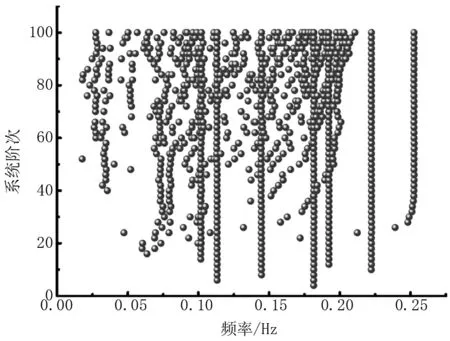
图1 全部识别结果

3.3 基于两阶段层次聚类的稳定轴自动识别

将聚类指标设为频率差1%,MAC差2%,分两阶段对识别结果进行聚类分析,将稳定点数量小于20的轴视为虚假轴并剔除。图2和图3分别表示第一阶段基于频率的稳定轴识别结果和第二阶段基于MAC的识别结果。

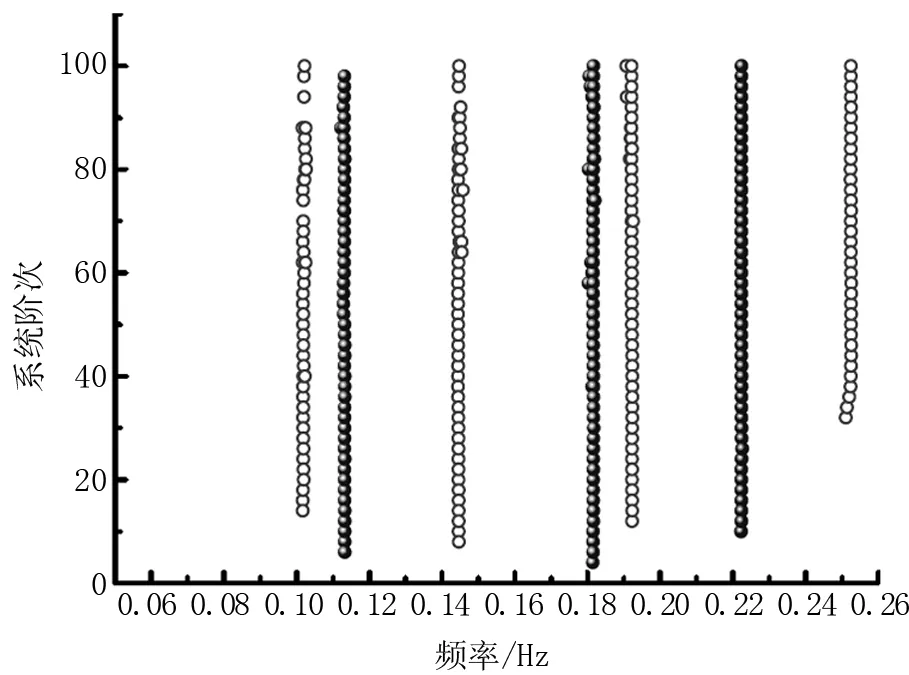
图2 一阶段基于频率的识别结果

图3 二阶段基于MAC的识别结果

从图2可以看到,第一阶段基于频率的稳定轴自动识别过程准确识别得到稳定轴,并剔除了其他虚假模态轴,第一阶段的聚类过程只以频率作为聚类指标,因此稳定轴在稳定图上相对连续。

从图3可以看到,基于MAC的二次聚类过程将第一阶段识别的稳定轴中的第一阶和第七阶稳定轴又划分成多个类,这说明,第一阶段基于频率的聚类过程识别得到的第一和第七阶频率稳定轴在振型上并不连续,存在振型识别结果异常点。第二～第六阶识别结果没有出现MAC异常点,说明第二～第六阶识别结果在频率和振型上都比较稳定。将第一和第七阶识别结果中振型不稳定点剔除将第二阶段聚类得到的每一类中数据量较少的类剔除,剩余的结果即聚类识别得到的稳定轴。

3.4 迭代的箱形图异常值检测

将两阶段聚类得到的稳定轴内的数据进行箱形图异常值检测。图4、图5、图6分别表示对一阶频率、一阶振型MAC和一阶阻尼比的箱形图检测结果。

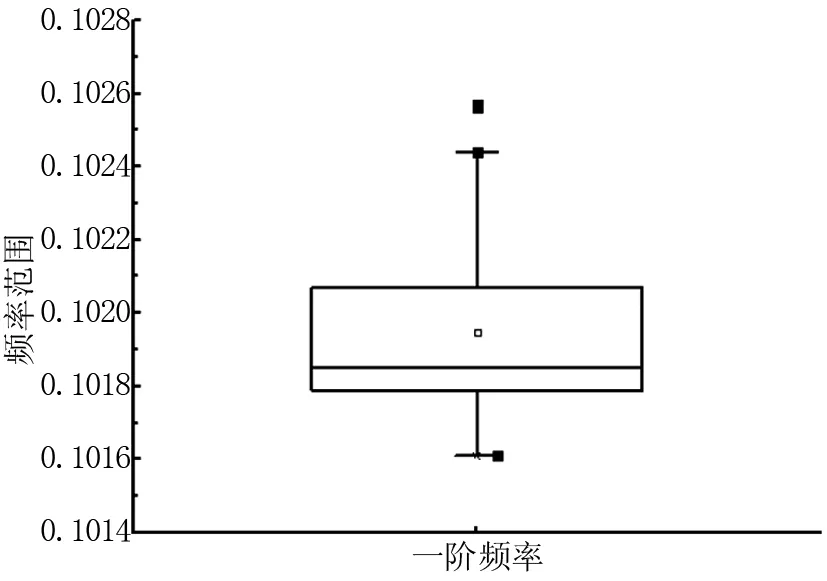
图4 一阶频率异常值检测

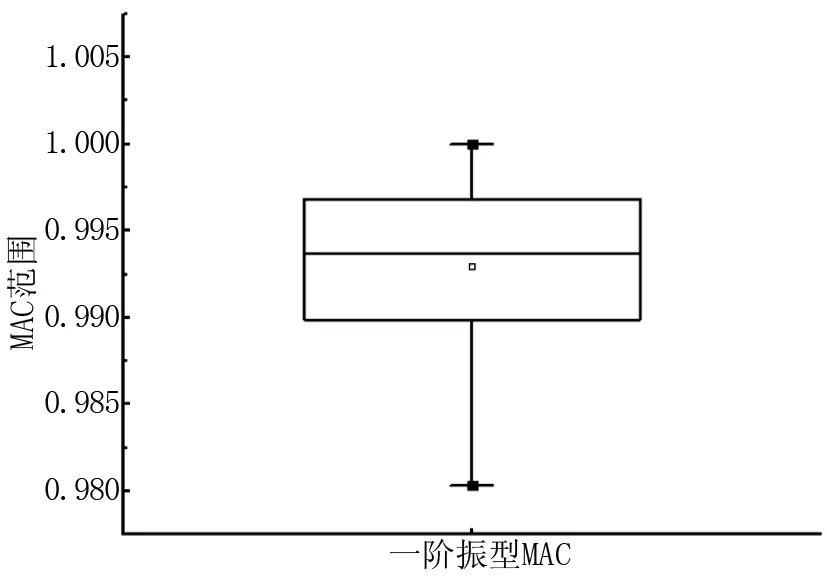
图5 一阶振型MAC异常值检测

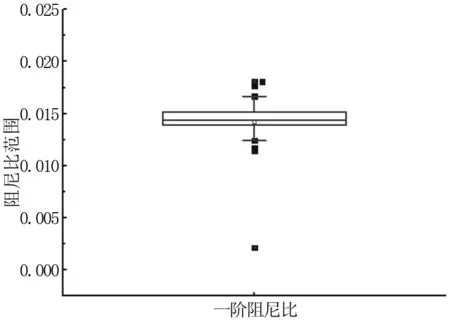
图6 一阶阻尼比异常值检测

从图4可以看到,尽管两阶段聚类过程识别得到频率和振型都稳定的稳定轴,但是频率仍然存在异常值,说明针对背景桥梁,基于经验确定的频率聚类指标偏大。图5表明振型MAC值没有出现异常值,说明基于经验选取的MAC聚类指标合理。图6结果表明一阶阻尼比识别得到较多的异常值,说明仅仅依靠频率和振型MAC指标的聚类结果不能得到合理的阻尼比识别结果。篇幅限制,其它阶稳定轴识别结果不再列出。

采用迭代的异常值剔除过程,对一阶识别结果进行异常值剔除,频率经过4次异常值剔除后不能检测到异常值,得到最终识别结果。振型由于原本不存在异常值,所以只进行对应的删除过程。识别阻尼比经过6次异常值剔除得到最终识别结果,在对频率和阻尼比剔除的过程中,同时剔除对应的其它识别结果。

以上过程说明,两阶段的聚类过程和基于箱形图的异常值诊断能够实现稳定轴自动识别,相较于原始聚类算法,能识别得到更准确的聚类结果。

4 结 论

(1)基于频率的聚类方法能够自动识别得到稳定轴,但识别结果中包含振型非稳定点。

(2)基于MAC的二次聚类过程能够剔除频率稳定轴中的振型非稳定点,得到频率和振型都稳定的识别结果。

(3)基于箱形图的异常值诊断方法识别得到较多的阻尼比异常值,解决传统聚类算法不能判别阻尼比识别结果可靠性的缺点。

(4)基于箱形图的异常值检测方法能够识别并剔除稳定轴中的异常值,提高基于固定指标的聚类结果的识别精度。