基于截断Pinball损失的支持向量机多类别概率估计
2023-06-07刘恒源倪中新陆贵斌
刘恒源 倪中新 陆贵斌
(上海大学经济学院 上海 201800)
0 引 言
多类别概率估计不仅提供了分类结果,还提供了分类结果的可信度信息,因此在数据挖掘和实际应用中具有重要作用。例如,在癌症诊断中,为调整治疗方法和药物剂量达到更好的效果,除了需要根据肿瘤的表型特征和基因组信息将患者标记为“A型”或“B型”之外,通常还希望报告一些有关分类决策的不确定性度量。一般来说,概率估计功能比分类功能更全面,也使分类任务更加灵活,体现在利用得到的条件概率pk(x)=p[Y=k|X=x],可以根据实际需求制定决策规则进行类别判断(二分类决策规则等价于以阈值0.5为界进行分类)。另外,概率估计结果可用于ROC、AUC等指标的计算,为学习器的性能评估提供方面。
传统上,对概率pk(x)=p[Y=k|X=x]的估计问题通常是通过多元logistic回归之类的回归技术或线性判别分析(LDA)和二次判别分析(QDA)之类的密度估计方法来解决。这些方法通常会对pk的函数形式(或其转换形式)做出某些模型假设。例如,多元logistic回归假设对数比率和X符合线性关系,LDA和QDA假设与每个子类关联的协变量X服从多元高斯分布。因此,这些方法虽然被广泛使用,但很难证明多元logistic回归中协变量线性关系的假设是正确的,此外,通常多元数据的高斯分布假设也存在争议。
支持向量机(SVM)由Vapnik等[1]提出,它不对数据分布进行假设,在文本分析[2-3]、生物医药[4-5]、图像处理[6-7]和垃圾邮件检测[8-9]等各种应用中显示出较高的预测准确性,但标准的SVM(C-SVM)的限制在于它直接关注分类,而不提供类别的估计概率。为解决这一问题,Platt[10]假设二分类正类条件概率p(x)=p[Y=+1|X=x]与SVM输出y∈0,1之间存在sigmoid连接函数,形式为p(x)=1/(1+exp(ay+b)),但是这种较强线性的假设在实际应用中很难满足。Wang等[11]提出了一种无模型的SVM概率估计方法,即没有对pk(x)的形式或每个子类的数据分布进行任何假设。他们通过训练一系列不同权重的二分类加权SVM(WSVM),然后结合所有WSVM的分类结果来构造p1(x),完成了二分类的SVM概率估计。Wu等[12]通过直接解决一系列多分类WSVM问题,将Wang等[11]的方案从二分类扩展应用到多分类。但由于直接求解多分类问题会增加复杂度,并且计算成本将随类别数K指数增加。为了降低复杂度和计算成本,Wang等[13]将K分类任务分解为K(K-1)个一对一二分类任务,应用Wang等[11]的方法进行二分类概率估计,然后利用公式耦合得到多类别的概率估计。
尽管这些方法实现了SVM的概率估计功能,但由于标准的SVM基于无界的Hinge损失函数,当某些样本点远离所属类时(即训练数据中的异常点或噪声点),会造成较大的损失,因此SVM往往会受到这类样本的强烈影响,导致分类和概率估计性能下降[14]。本文通过限制无边界的Pinball损失提出一种稳健的截断Pinball损失并应用于SVM(T-Pin-SVM)以提高概率估计和分类的准确度。数值模拟表明所提出的T-Pin-SVM一定程度上弥补了C-SVM噪声敏感的缺点,可以提供比C-SVM更高的概率估计精度。同时,相对于Pin-SVM,截断也使得T-Pin-SVM的稀疏性增强,降低了测试阶段的计算成本。另一方面,T-Pin-SVM涉及非凸优化,这比C-SVM的二次凸规划求解更具挑战性,本文应用Difference Convex(DC)算法,通过求解一系列凸子问题解决非凸优化。
1 方法和理论
本节提出了一种截断Pinball损失函数应用于SVM(T-Pin-SVM),讨论了它的噪声鲁棒性、稀疏性和Fisher一致性,并且给出了T-Pin-SVM应用于多分类概率估计的算法流程。
1.1 T-Pin-SVM模型
Pinball损失与分位数有关,其应用于SVM的合理性已在[15]中进行了全面的讨论。我们提出了Pinball损失的改进版本,即截断Pinball损失(见图1),可以表示为:
式中:l1(u)=max{u-a,0},当α→+∞时,截断Pinball等价于Pinball损失;当α→+∞且τ=0时,等价于Hinge损失,因此本文提出的截断Pinball是Hinge和Pinball的广义形式。
考虑K=2的二分类问题,标签y被编码为-1、1,SVM分类器表示为f(x)=wTφ(x)+b,其中φ(·)∈HK表示可再生内核希尔伯特空间(RKHS),它可以将低维空间映射到高维空间,为解决线性不可分问题提供了可能。应用截断Pinball损失的SVM称为T-Pin-SVM,可以表示为:
(1)
某个权重πm(m=1,2,…,M)下的加权T-Pinball-SVM可以表示为:
(2)
式中:1-πm、πm(0≤π≤1)分别表示类别1、-1的权重。
1.1.1噪声鲁棒性和稀疏性
一般不要超过两行。在二分类任务中,基于Hinge损失(l(u)=max{0,u})的C-SVM模型求解等价于两类点到超平面的最小距离之和取最大,这意味着最终影响超平面的仅与少数具有最小距离的点有关,并且这些点通常位于超平面附近,因此C-SVM对超平面附近的噪声敏感。另一方面,注意到当u≥0且递增时,Hinge损失线性增长且无界的,这意味着当某些异常点完全偏离本身类别而混入其他类别时(如标签错误),对其的惩罚较大而影响整体的损失函数,因此C-SVM对这些位置的点同样敏感。
基于Pinball损失(lτ(u)=max{u,-τu},0≤τ≤1)的Pin-SVM模型求解等价于两类点到超平面的q分位数距离之和取最大。图1显示了基于两种SVM的分类差异。在Pin-SVM中,由于某一类样本点到超平面距离的集合取q分位数的点才会影响到超平面,因此即使超平面附近有噪声点,其占比也相对较少,这使得Pin-SVM本身就具有一定的噪声不敏感性,然而和Hinge损失相似,Pinball损失对错误分类的样本惩罚是无界的。因此,为了增强噪声鲁棒性,本文利用参数a截断Pinball损失以避免错分类样本的无界惩罚。a的取值决定了截断的位置并影响了SVM的表现,更多细节将会在实验部分介绍。另外它与左侧截断不同[16],右侧截断更关注那些严重偏离所属类的样本点。
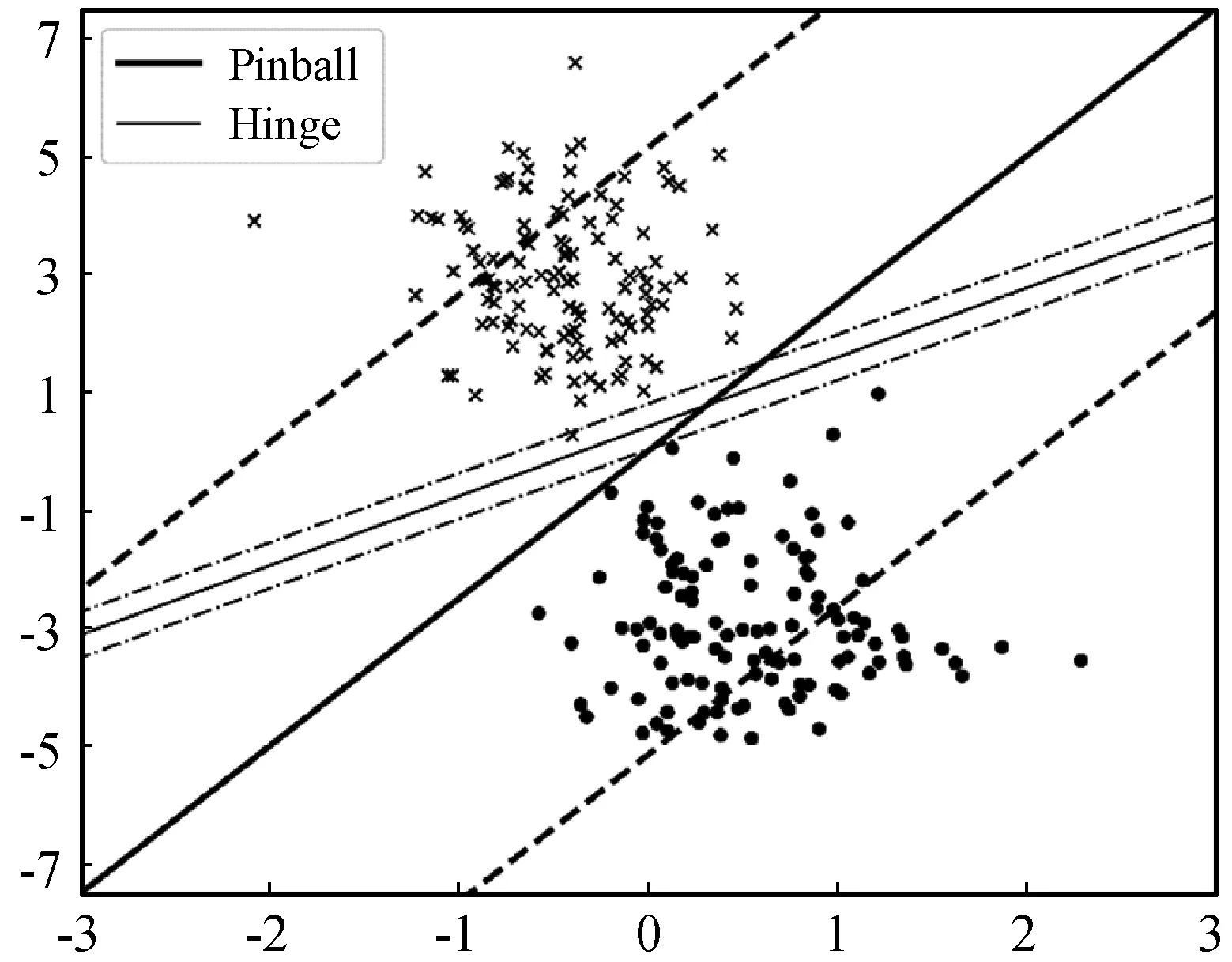
图1 基于Hinge和Pinball的SVM分类差异
由于Pinball损失没有水平区域,其次梯度在任何地方都不等于零,因此Pin-SVM失去了稀疏性,这将导致测试阶段较高的计算成本。而对于T-Pin-SVM而言,式(1)的最优化条件可以表示为:
0∈w-∑∂L(1-yif(xi))
式中:0表示全0向量;∂L(·)定义为次梯度函数。
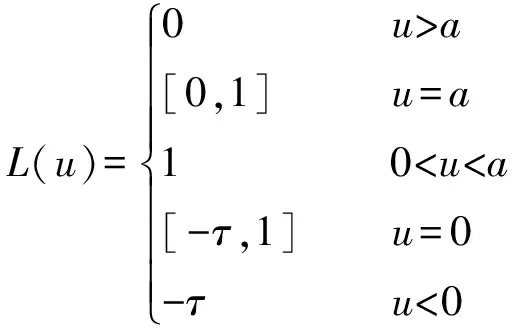
结合图2可以发现,当a减小,更多的样本点倾向于落入损失函数水平,次梯度为0,意味着w的分量为0,稀疏性增强。反之,a增大,稀疏性降低。因此,本文定义w的分量不等于0的样本为支持向量(SVs),并用支持向量占训练样本的比例(SVs%)衡量稀疏性(在概率估计中通过平均所有权重下的支持向量比例后再平均K(K-1)个二分类任务的比例得到)。由于Pinball损失没有水平区域,所以Pin-SVM的支持向量比例为常数。
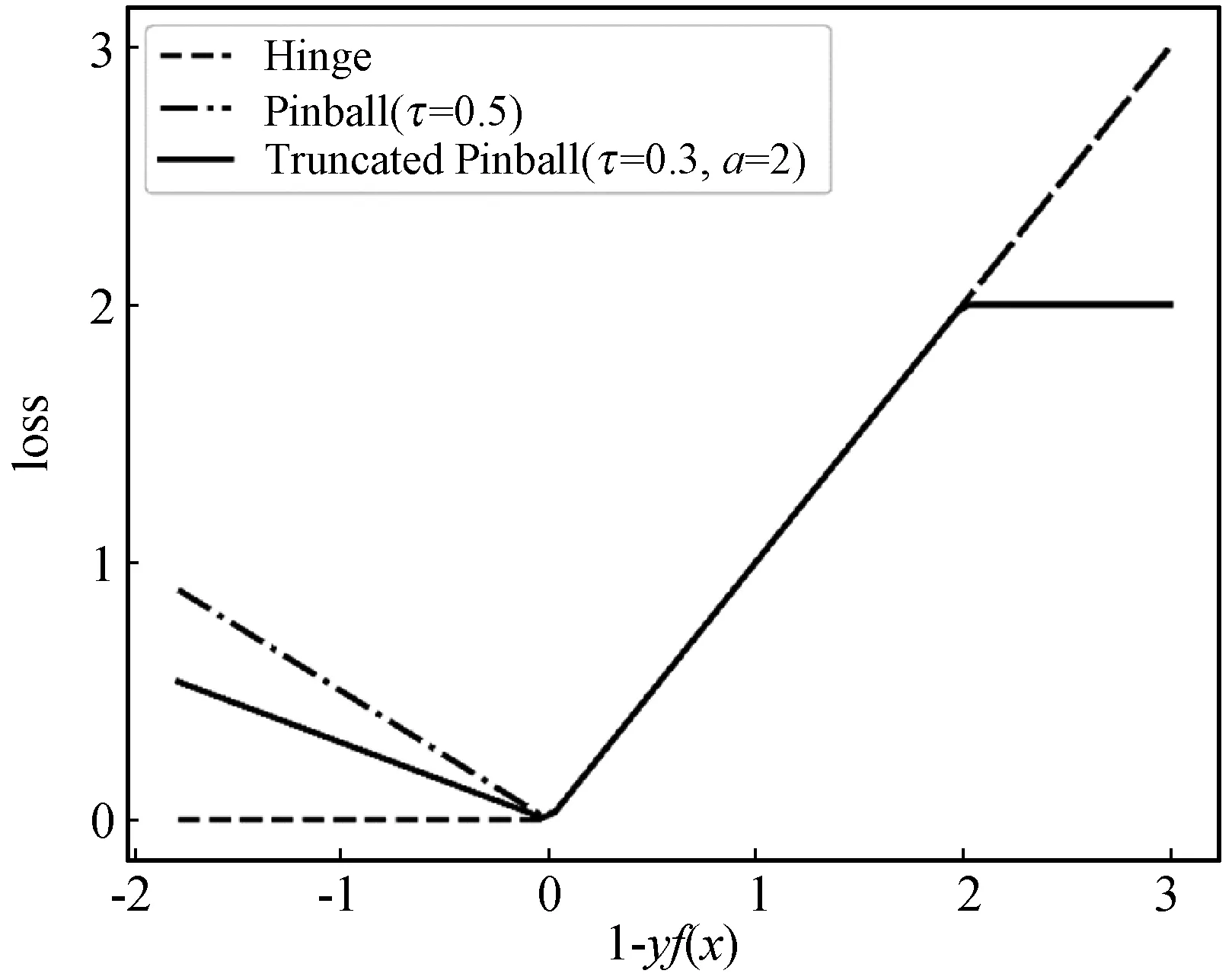
图2 Hinge、Pinball和截断Pinball三种损失函数
1.1.2Fisher一致性

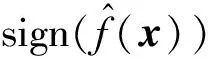
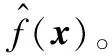
当0 当1 当a>2时: 1.2.1T-Pinball-SVM二分类概率估计 (3) 输入:C,σ,a,τ,πm,max_iter (1) 初始化β0=0; (2) for t=1 tomax_iterdo (6) 通过yi(wTφ(xi)+b)=1求解b*; (7) 平均所有b*得到b; (9) 利用式(6)更新βi; (10) ifβt=βt-1then (11) Break; 具体过程如下: 对于式(2)的非凸问题,可以表示为min(Qvex+Qcav),其中: (4) (5) 定义: (6) 式中:s=1-a;Iyif(xi) (7) 构建拉格朗日函数: ∑αi(ξi-1+yif(xi)) 求导得到: 将解得的w代入拉格朗日函数得到对偶方程: (8) 1.2.2概率耦合 在得到K(K-1)个二分类的成对条件概率估计后,可以通过概率耦合得到K个类别的概率估计,其中类别概率定义为pj(x)=p(Y=j|X=x),j=1,2,…,k。由于qj|(j,j′)(x)+qj′|(j,j′)(x)=1,可以得到: (9) 从而对于任意类别j∈{1,2,…,K},j′≠j,可以通过式(9)完成多类别的概率值估计。 为了衡量三种SVM概率估计性能,我们使用l1范数误差和l2范数误差以评估对比模型差异,由于实际数据没有真实的概率值,本文使用准确率ACC评估分类结果以反映概率估计的表现,其中分类结果根据概率值最大的标签确定。对于每一数据集,我们测试了不同参数组合下T-Pin-SVM的表现,其中τ∈{0.2,0.5,0.8},a∈{1.5,2,2.5}。每组参数下的性能评估结果均利用随机训练集训练,对同一测试集重复测试50次得到,括号中数值为标准差,结果均乘以100展示。 ACC=(TP+TN)/(TP+FN+TN+FP) 式中:TP和TN表示真阳和真阴数;FN和FP表示假阴和假阳数。 (1) 模拟数据1生成:定义任意样本点(x1,x2)满足方程: 对于模拟数据,均随机抽取500个样本,其中30%作为测试集,其余70%作为调整集和训练集用于C的选择和模型训练。另外,对于500个样本,随机选择20%将其标签以相等概率的更改为其他任意类别以增加噪声。 T-Pin-SVM和Pin-SVM的主要区别在于T-Pin-SVM通过截断位置a对损失进行截断以限制错误分类样本的无界损失,因此a影响了T-Pin-SVM概率估计的性能,另外a的取值也影响了落入损失函数水平区域样本的数量,决定了T-Pin-SVM的稀疏性。表1显示了T-Pin-SVM和Pin-SVM模型的概率估计结果。可以发现,当固定相同的τ值,a的不同设定,5个数据集的大多数概率估计误差指标(l1和l2)均会下降,这表明截断会提升Pin-SVM的噪声鲁棒性,显示了T-Pin-ball在概率估计中的良好表现。另外,在模拟数据和实际数据Pima中,T-Pin-SVM的SVs均小于Pin-SVM,且随a减少而降低,稀疏性增强。同样,在实际数据Vote和Ionosphere中,相比后两种a的取值,a=1.5也会引起稀疏性增强。而在a=2和a=2.5参数条件下,T-Pin-SVM的稀疏性指标SVs均与Pin-SVM无差异,表明在这两个数据集中,损失均小于2,截断不起作用。 表1 不同参数组合下T-Pin-SVM和Pin-SVM模型的 续表1 表2显示了T-Pin-SVM、Pin-SVM和C-SVM在5个数据集中的概率估计对比结果。可以发现,C-SVM在稀疏性指标SVs上的表现明显优于T-Pin-SVM,这是由于在C-SVM中,对于正确分类的点Hinge损失梯度为0,且在所有数据集中,正确分类的点显然多于噪声点,在T-Pin-SVM中,高于某一损失值的噪声点(取决于a)才对应零梯度,而在Pin-SVM不存在零梯度。C-SVM这种强稀疏性也使得测试和调整参数阶段较少的计算成本,T-Pin-SVM的计算成本也少于Pin-SVM。对于类别概率的估计,除Pima数据集外,T-Pin-SVM的结果均优于其他两个模型。 表2 T-Pin-SVM、Pin-SVM和C-SVM概率估计性能对比 针对SVM在多类别概率估计中存在的噪声敏感问题,本文提出了一种截断的Pinball损失,讨论了它的噪声鲁棒性和稀疏性,并证明了基于该损失的T-Pin-SVM具有Fisher一致性。另外,为降低求解复杂度和计算成本,本文将K类别概率估计任务划分为K(K-1)个二分类任务,利用Fisher一致性得到二分类概率估计后,再利用耦合公式实现了多类别概率估计。对于截断Pinball损失导致的非凸问题,本文应用了DC算法求解。模拟数据和实际数据表明,相比于C-SVM、Pin-SVM,本文所提出的T-Pin-SVM可以降低概率估计的误差,提高分类准确性,并且相对于无边界的Pinball损失,它的稀疏性更强。 另外,类不平衡对SVM也有较大影响,进一步的研究可以结合类不平衡提高SVM概率估计准确性。
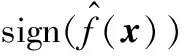
1.2 T-Pinball-SVM多分类概率估计

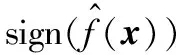
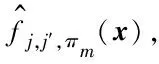

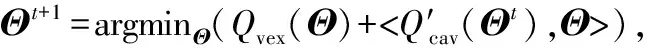
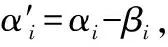
2 实验与结果分析
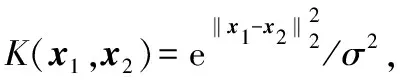
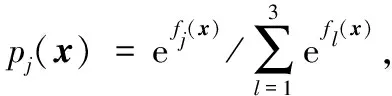
2.1 截断位置a的影响
2.2 不同SVM模型的性能评估
3 结 语
