基于代价敏感卷积神经网络的遥感影像分类

赫晓慧 李志强 李盼乐 田智慧 周广胜,3

1(郑州大学地球科学与技术学院 河南 郑州 450052) 2(郑州大学信息工程学院 河南 郑州 450001) 3(中国气象科学研究院郑州大学生态气象联合实验室 河南 郑州 450052)

0 引 言

随着对地观测和遥感技术的迅速发展,高分辨率数据成为重要的信息来源,比传统图像包含更多的结构化和统一的数据,对高分遥感数据的挖掘应用在社会经济、政治、国防等方面建设中的重要性日益凸显。遥感影像分类是指根据遥感影像的内容,自动为每个遥感影像像素分配一个特定的语义标签,由于其在土地利用、城市规划、土地资源管理等方面的重要应用,已成为遥感图像解译领域的一个重要的研究内容[1-4]。

近年来,随着深度学习方法的普及,在包括图像分类[5]、对象识别[6]和语义分割[7]在内的许多应用中取得了瞩目的成绩。深度学习模型可以通过深层架构神经网络来学习更强大、抽象和有区别的功能,而无需大量的工程技能和领域专业知识。所有这些深度学习模型,尤其是卷积神经网络(CNN),更适用于遥感图像分类并取得优异的结果[8-21]。

尽管基于CNN的方法已大大提高了分类准确性,但是依然没有解决遥感影像分类中类不平衡问题,即样本比例不平衡和难易样本不平衡。样本比例不平衡是指在一个数据集中,一个类的样本很少,即少数类,另一类样本很多,即多数类[22-24]。在遥感影像分类问题中,类别的样本比例存在严重不平衡性,例如背景、道路和建筑物三分类时,背景像素占绝大多数,道路和建筑物占比较小。以马萨诸塞州数据集中1 108幅训练集为例,道路像素平均比例为4.77%,最小占比不到1%,最大也不过20%。难易样本数量不平衡是遥感影像分类中固有的问题。困难样本是指难以分类像素,例如,被树木遮挡的道路像素;简单样本就是可以轻松分类的像素。传统的分类模型给予难易样本相同的误分类代价,包含较多简单样本的类别对整体损失值会起到决定性的影响,而含有较少困难样本的类别对损失的影响微乎其微,其必然导致模型倾向于含有较多易分训练样本的类别进行预测。遥感影像包含丰富的目标信息,不同样本比例差距更大,而且相互遮挡严重,所以解决遥感影像分类中类不平衡问题是至关重要的。

代价敏感学习是从算法层面解决不平衡问题的主要方法。Kukar等[25]表明,将代价信息纳入损失函数可以提高性能。但是,它们的代价是在网络的多个运行中随机选择的,并且在每次运行的学习过程中保持不变。Chung等[26]提出了一个新的CoSen损失函数,用回归损失代替了传统的Softmax,但是该损失函数存在当网络加深使梯度减小的问题,不适用于深度神经网络。Khan等[27]提出了CoSen卷积神经网络,同时对网络的参数和cost参数进行优化,并在多种经典损失函数(MSE loss,SVM loss,CE loss)上进行实验,提升了卷积神经网络的分类准确度,有效地解决了样本不平衡的问题,但是没有考虑到简单样本和困难样本的关系。

以上方法证明代价敏感学习对解决类不平衡问题的有效性,但是都还存在着一些不足,并且没有应用到遥感影像分类困难样本中。为了解决遥感影像分类中类不平衡问题,本文将代价敏感学习与深度学习相结合,提出自适应样本特征的代价敏感遥感影像分类算法(SCoSen-CNN)。算法的核心思想是:首先,分别为每个类分别建立损失函数,同时对损失函数添加自适应正负样本平衡因子,降低样本不平衡问题对分类模型精确度的影响,加速模型参数的自动更新。然后引入误分类代价矩阵,不同误分类给予不同的误分代价,增加模型对困难样本的学习能力,在一定程度上缓解了不平衡数据对模型分类的影响。并且提出一种用于联合交替优化网络参数和类别代价敏感因子的算法。本文算法适用于不平衡遥感影像二分类和多分类问题。

1 自适应样本特征的代价敏感分类算法

在为了解决遥感影像分类任务中数据不平衡问题,本文提出一种自适应样本特征的代价敏感损失函数,将该损失函数引入到卷积神经网络(CNN)中,以构建成代价敏感的卷积神经网络,可以有效地解决遥感影像分类任务中数据不平衡问题,最后通过代价敏感的卷积神经网络的分类结果即为最终的分类结果。具体的算法流程如图1所示。

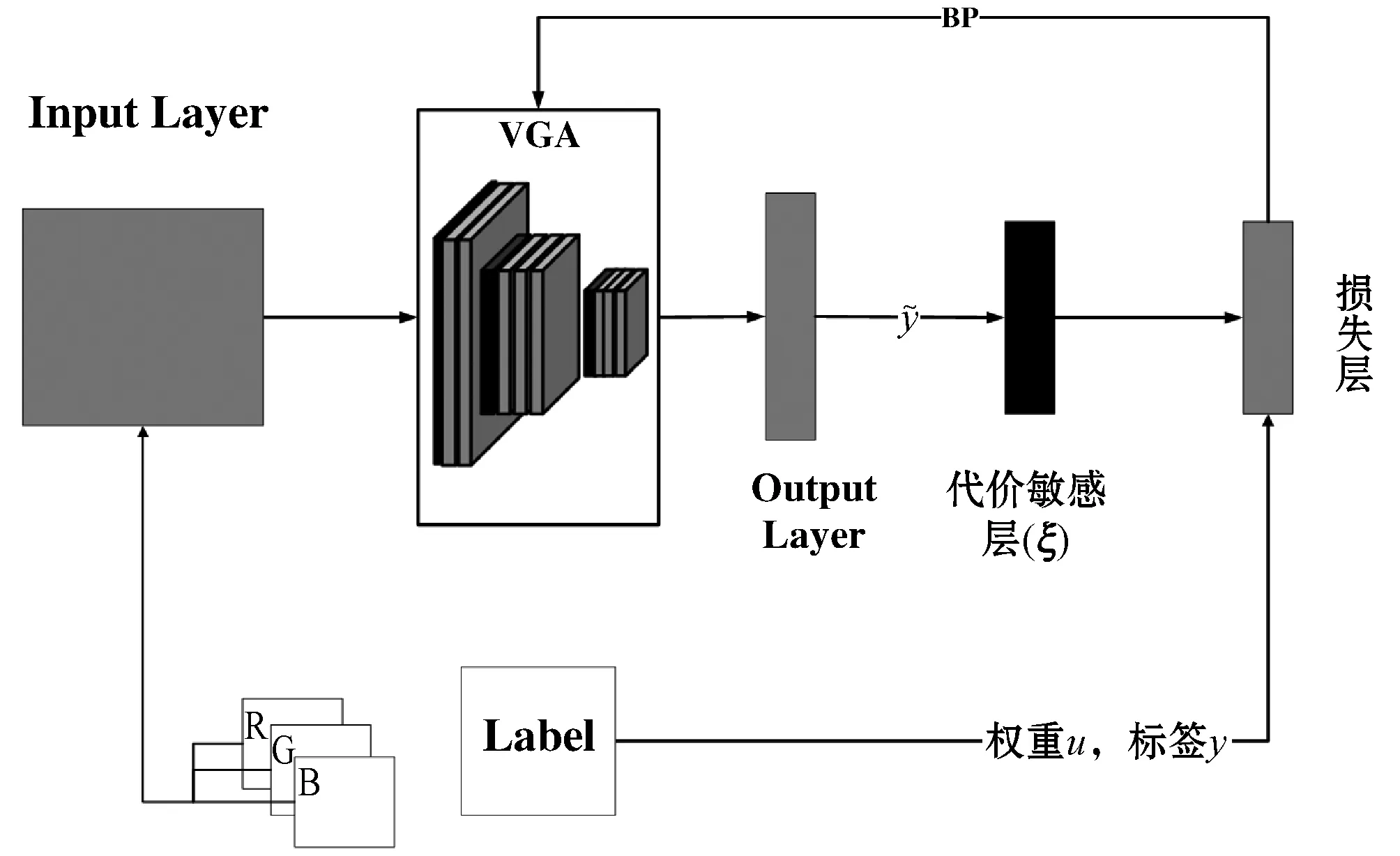
图1 本文算法总体流程

SCoSen首先在训练阶段对各个类分别建立损失函数,计算每一个类别的平均误差,将所有类的平均损失值相加,并且对训练样本进行特征统计,根据统计的结果损失函数进行动态加权(u),最终的损失值由每个类加权损失的平均值相加构成,以解决样本不平衡问题。然后在CNN的输出层和损失层之间增加代价敏感层,利用代价矩阵ξ对模型的输出赋予不同的误分类代价,从而解决困难样本与简单样本不平衡的问题。

1.1 传统损失函数

遥感影像分类使用损失函数通常定义如下:

(1)

式中:y(i)(w,b)是模型第i个样本的预测输出;w、b是网络权重和偏差;M是训练样本总数;d(i)∈{0,1}1×N是第i个样本标签,N表示输出层中神经元的总数,即类别数。

该函数可以表示为训练集的平均损失,其中,l(*)可以是任何合适的损失函数,如均方误差(MSE)、交叉熵损失函数(CE)等,本文中使用的是交叉熵损失函数,如式(2)所示。

(2)

CNN模型在训练集上表现不佳时,会造成更大的误差。学习算法的目的是找到最优参数(w*,b*),该参数给出最小的可能成本E*。因此,优化目标为:

(3)

遥感影像中类别的样本比例存在严重的不平衡性,传统的损失函数无法区分易分样本和稀有样本,较多的样本造成大量的损耗,导致模型倾向于简单样本学习,而忽略了稀有困难样本。

1.2 自适应样本特征的交叉熵损失函数(SCE)

针对遥感影像训练集中样本比例不平衡问题,本文将每个类别的损失分别考虑,分别构建一个损失函数,然后计算每一个类别的平均误差:

(4)

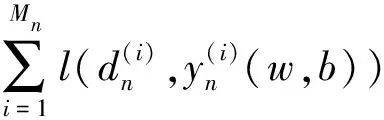
然后将所有类的平均损失值相加,最终的损失值由每类损失的平均值相加构成,以减小不同类别之间训练样本数量不平衡性的影响,平均类别损失如式(5)所示。

(5)

同时,通过原始(训练)数据集中的原始类比例,在损失函数的计算中添加自适应样本特征的权重,将式(5)改进为自适应样本特征的加权交叉熵损失函数(SCE)。其中权重u定义如下:

(6)

式中:N是初始数据集中的类数;un是第n类样本所添加权重;pn是初始数据集中第n类样本占总样本的比例。式(7)展示了自适应样本特征的加权损失函数:

un∈U(D)

U(D)=(u1,u2,…,uN)

(7)

式中:每个类的权重un从包含权重的权重U(D)集合中获取,权重U(D)在学习过程开始时针对初始数据集D计算得出,不需要通过大量的实验进行调整,并且适应随着训练过程变化而变化的数据分布。

SCE通过对每个类都建立损失函数,并且添加权重调节因子,最终的损失值由每个类的加权损失的平均值相加构成。尽管SCE平衡了样本比例,但它并未区分简单/困难样本。本文将SCE函数重塑为轻量化简单样本损失,从而将训练重点放在稀有困难样本上。

1.3 自适应样本特征的代价敏感交叉熵损失函数(SCoSen-CE)

针对遥感影像分类中困难样本与简单样本不平衡问题,本文将代价敏感学习应用到深度学习中,使不同类别之间发生误分类获得不同的惩罚代价,将SCE改进为自适应样本特征的代价敏感(SCoSen)损失函数:

(8)

传统代价矩阵通常具有以下形式:

(9)

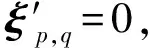
(10)

这种代价矩阵可能将相应的损失增加到很大的值。在CNN训练期间,这种网络损失可能使训练过程不稳定,并可能导致误差函数不收敛。本文使用替代的代价矩阵。

相较于SCE,SCoSen-CE给激活值乘以一个代价矩阵的代价向量,将误分类代价考虑在内。不仅通过原始(训练)数据集中的原始类比例,在计算中添加自适应样本特征的权重,平衡了训练集的样本比例,而且可以区分简单和困难样本,减少了简单样本的损失值,将训练的重点放在了分类困难的稀有样本上。接下来给出本文使用的代价矩阵。

1.4 代价矩阵

本文使用一个适合于卷积神经网络(CNN)训练的代价矩阵ξ。代价矩阵ξ用于修改CNN最后一层的输出(在Softmax层和Loss层之前),如图2所示。然后在计算分类损失之前将得到的激活值(activate)压缩在[0,1]之间。

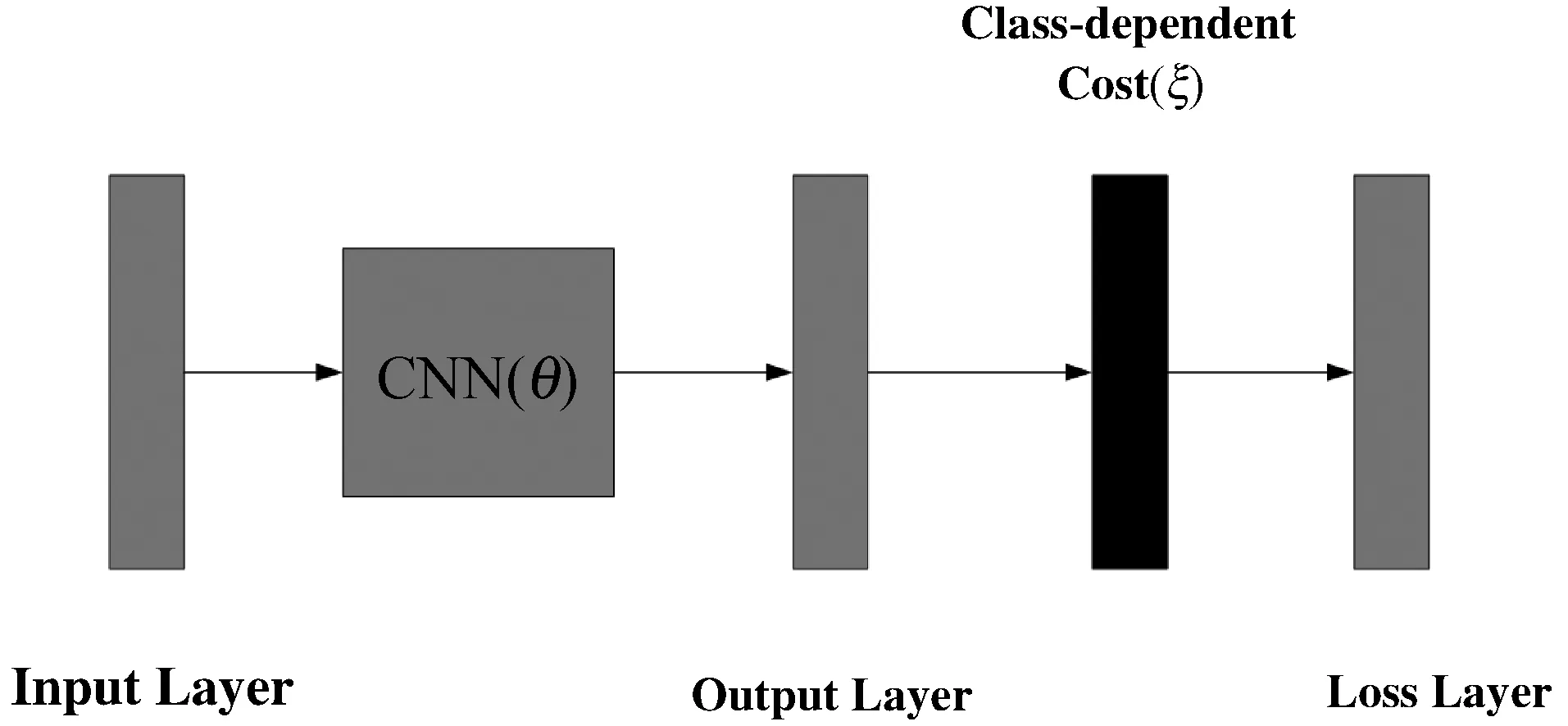
图2 训练过程中使用的CNN参数(θ)与类相关 代价矩阵(ξ)和权重(w)的关系

对于CNN,分类决策是针对具有最大分类得分的类别做出的。在训练过程中,修改分类模型权重以重塑分类模型的置信度(分类概率),使所需分类具有最大分数,而其他分类具有明显较低的分数。由于较少的类别在训练集中所占的比例不足,因此引入了分数级代价(score-level costs),以加强对比例小的类别进行正确分类。因此,根据函数(F)使用代价矩阵ξ修改CNN输出(o),计算如下:

(11)

式中:y表示修改后的输出;p是所需的类;F:R→R表示一个函数,其确切定义取决于损失层的类型。类的代价会扰乱分类模型的置信度,这种扰动可以使分类模型将重点放在数量少且难以分离的类上。引入的代价矩阵具有以下的性质:

(1) 所有与代价无关的损失函数的代价矩阵ξ是全1矩阵,即1p×p。

(2) 代价矩阵ξ中的所有代价均为正,即ξ>0,并且使其所有值都在(0,1]范围内,即ξp,q∈(0,1)。

新的代价矩阵的形式如下:

(12)

与传统代价矩阵不同的是,本文中的代价因子N不是一个人工判别的固定值,而是利用类对类(c2c)的可分离性,通过估计类内样本与类间样本之间的差异来衡量,不需要人工对代价矩阵进行判别,并且使用联合优化算法,在模型迭代的过程中不断地对代价因子进行优化,以得到合适的代价因子N。

根据以上描述的性质,本文引入的代价矩阵ξ既不会过度增加CNN输出激活,也不会将其减少为零输出值。并且可以实现平稳的训练过程,从而可以正确更新模型参数。

1.5 最佳参数优化

当使用SCoSen-CE时,由于平衡因子u可以通过训练样本自适应调节,所以CNN的目标是共同学习参数θ和与类相关的损失函数参数ξ。对于联合优化,本文通过保持一个参数固定不变并使另一个参数最小化代价来解决这两种参数优化,如算法1所示。具体来说,为优化θ,我们使用随机梯度下降和误差的反向传播。接下来,为优化ξ,再次使用梯度下降算法计算更新参数。与类相关的损失函数参数ξ还取决于类-类(class-to-class)的可分离性,即使用当前的参数网络估计CNN所产生的分类误差以及总体分类误差。类对类(c2c)的可分离性是通过估计类内样本与类间样本之间的差异来衡量的。换句话说,它测量同类样本之间的距离与不同类之间分隔边界的大小之间的关系。

算法1参数(θ,ξ)的迭代优化

输入:训练集(x,d),验证集(xv,dv),最大迭代值(MeP),θ的学习率(γθ),ξ的学习率(γξ)。

输出:参数学习(θ*,ξ*)。

1.Net←construct_CNN()

2.θ←initialize_Net(Net)

//随机初始化

3.ξ←1,val-err←1

4.fore∈[1,MeP]do

//迭代次数

5.gradξ←compute-grad(x,d,F(ξ))

6.ξ*←update-CostParams(ξ,γξ,gradξ)

7.ξ←ξ*

8.forb∈[1,B]

//样本训练次数

9.outb←forward-pass(xb,db,Net,θ)

10.gradb←backward-pass(outb,xb,db,Net,θ,ξ)

11.θ*←update-NetParams(Net,θ,γθ,gradb)

12.θ←θ*

13.endfor

14.val-err*←forward-pass(xv,dv,Net,θ)

15.ifval-err*>val-errthen

16.γξ←γξ*0.01

//梯度下降速度

17.val-err←val-err*

18.endif

19.endfor

20.return(θ*,ξ*)

为了计算c2c之间的可分离性,首先计算cP类中的每个点与其所属的cP的最近邻居和cq类中的最近的邻居之间的距离。类间距离通过特征空间中计算,其中每个点都是4 096维特征向量(fi:i∈[1,N′],N′是属于cP类的样本)从倒数第二个CNN层(在输出层之前)获得。然后,为一个类中的每个像素点找到类内距离与类间距离的平均值,并计算平均值的比率以找到c2c可分离性指数。两个类p和q之间的类可分离性定义为:

(13)

式中:dintraNN(fi)为类间距离;dinterNN(fi)为类内距离。

为了避免过度拟合并证明该步骤在计算上可行,本文在一个小的验证集上测量c2c可分离性。而且,发现c2c的可分离性与每个阶段的混淆矩阵相关。因此,本文在每十个周期之后计算一次,以最大限度地减少计算开销。这表明类别相关代价(ξ*)的最佳参数值不应与训练数据分布中类别的频率相同。以下代价函数用于梯度计算以更新ξ:

(14)

式中:Eval是验证误差。矩阵T定义如下:

(15)

式中:μ和σ表示参数,分别为使用交叉验证的集合;R表示当前的分类错误作为混淆矩阵;S表示c2c类可分离性矩阵;H表示使用直方图向量h定义的矩阵,该矩阵对训练集中的类的分布进行编码。矩阵H和向量h的联系如下:

(16)

式中:c是给定数据集中所有类的集合。最优ξ*的最小化目标可以表示为:

(17)

使用梯度下降算法优化式(15)中的代价函数,该算法计算更新步骤的方向如下:

-(va-vb)1T

(18)

式中:va=vec(T);vb=vec(ξ);J表示雅可比矩阵。为了合并F(ξ)对验证误差Eval的依赖性,仅在Eval减小时才采取更新步骤。

2 实验与分析

2.1 数据集

为了验证所提出损失函数的有效性,建立类不平衡的高分辨率遥感影像数据集。如图3所示,数据集覆盖了津巴布韦的多个城市、郊区和农村的遥感影像,包括原影像以及各自影像目标的标签影像,有道路和建筑物两类目标样本,统计数据集192幅训练样本。通过对该数据集每幅影像的像素和平均像素统计发现,单幅影像中背景占有50%以上的像素,平均占比高达80%,而道路和建筑物最大的占比也只有30%,最小不足1%,平均占比只有10%左右,如表1所示,样本之间的比例是极其不平衡的。该数据集的原影像分辨率非常高,分辨率为0.28 m,而且遥感影像来源于开源的Bing地图和OSM的矢量数据,可以根据需要自由地进行扩展。

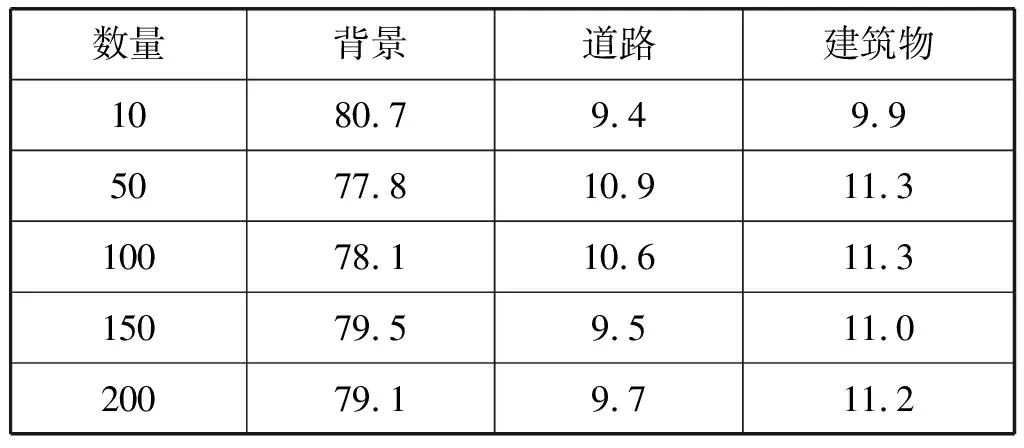
表1 不同数量下各类平均像素占比(%)

该数据集提供了233幅图像,图片为1 500×1 500像素的RGB影像,地面分辨率约为0.28 m,分为建筑物和道路两个数据类,有大量的建筑物和清晰的道路数据。数据集包含训练集192幅卫星照片及其对应标注图,测试集41幅卫星照片及其对应标注图,验证集5幅卫星照片及其对应标注图,每一幅卫星照片中都包含有道路目标。图3给出该数据集的目标信息。

图3 数据集展示

网络的训练采用了数据集中训练集和对应标注图,并且通过数据增强的方法对数据集进行扩充,将原始图片从1 500×1 500像素缩放为92×92像素及对应的24×24像素的标注图,使用其测试集共41幅影像及其标注图对本文提出的损失函数性能进行评估。

2.2 评价指标

在遥感影像目标检测中,正样本类别的实例很少,负样本类别过多可能会影响模型评估表现。由于错误率不能很好地评价样本不平衡的数据集,所以本文采用准确率(accuracy)、召回率(recall)、F1-score和精度(precision)进行衡量:

式中:FN是正样本判定为负样本;FP是负样本被判定为正样本;TN是负样本被判定为负样本;TP是正样本被判定为正样本。

2.3 卷积神经网络

VGGNet使用了3个3×3卷积核来代替7×7卷积核,2个3×3卷积核来代替5×5卷积核。在保证具有相同感知野的条件下,提升了网络的深度,多层的激活层具有更好的非线性表达能力,并且减少了网络的参数,在一定程度上提升了神经网络的效果,大大延长了训练时间。为了验证方法的有效性,本文提出一个深度卷积神经网络VGA来学习用于图像分类任务的鲁棒性特征表示。网络结构如图4所示,该网络受启发于VGGNet,不同的是,为了加速收敛与避免参数过多引起的过拟合问题,本文的网络在输出层和提出的SCoSen损失层之前只有一个的全连接层。

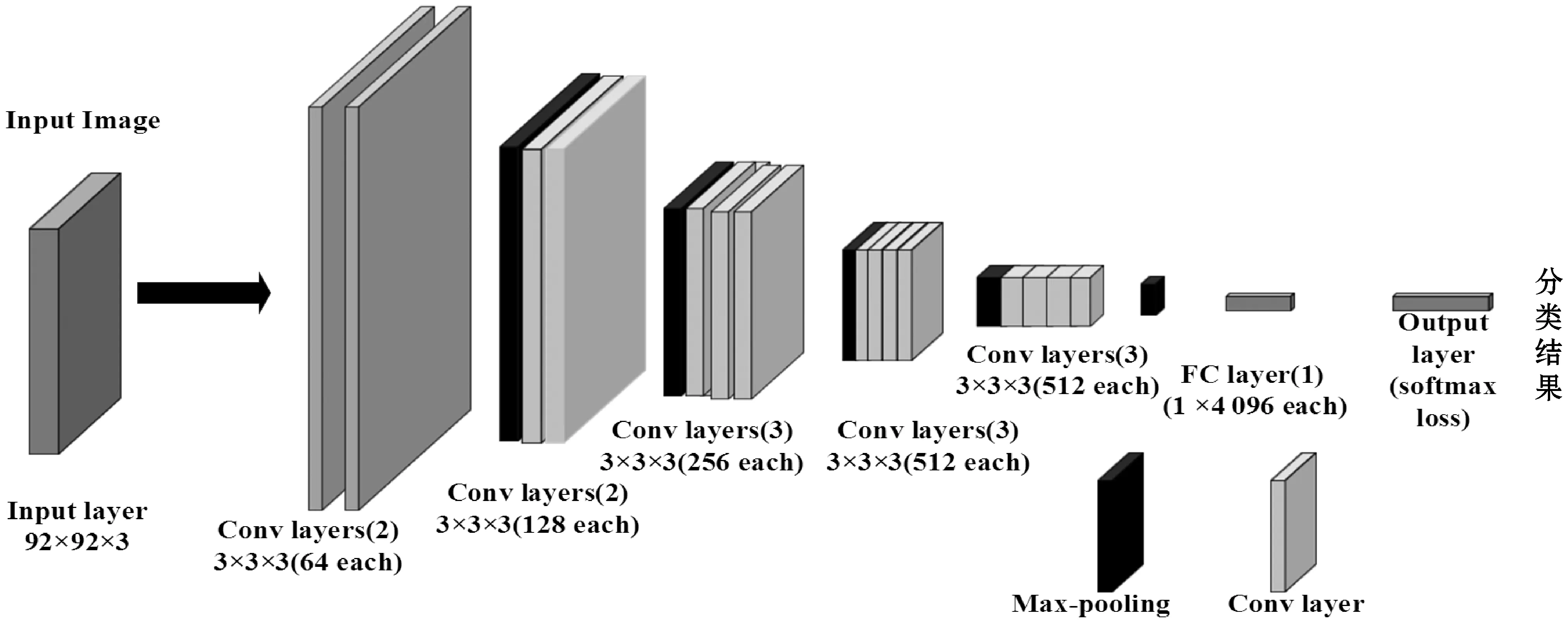
图4 VGA网络结构

本文使用VGG16[28]的预训练模型初始化模型的前16层,并为最后全连接层设置随机权重。然后,以相对较高的学习率训练整个网络,以得到最优的网络参数。并且使用本文介绍的修改后的自适应样本特征的代价敏感损失函数(SCoSen-CE)对网络进行训练。

2.4 实验结果及分析

本文以代价敏感的交叉熵损失函数结合卷积神经网络VGA为基础的遥感影像多目标分类,在VGA实验中,分别使用交叉熵损失函数(CE)、SCE、CoSen-CE、Focal loss和SCoSen-CE进行实验,取得了良好的实验结果,验证了本文方法的有效性。并且通过可视化和数值两个方面进行结果的分析,证明本文方法的有效性。

2.4.1对比实验结果分析

在正负样本不平衡的遥感影像数据集下,通过CE、SCE、CoSen CE、Focal loss[29]和SCoSen CE等方法进行对比,证明了SCoSen CE良好的性能。

使用建立的高空间分辨率数据集的41幅测试图片进行测试,所得结果指标如表2和表3所示。

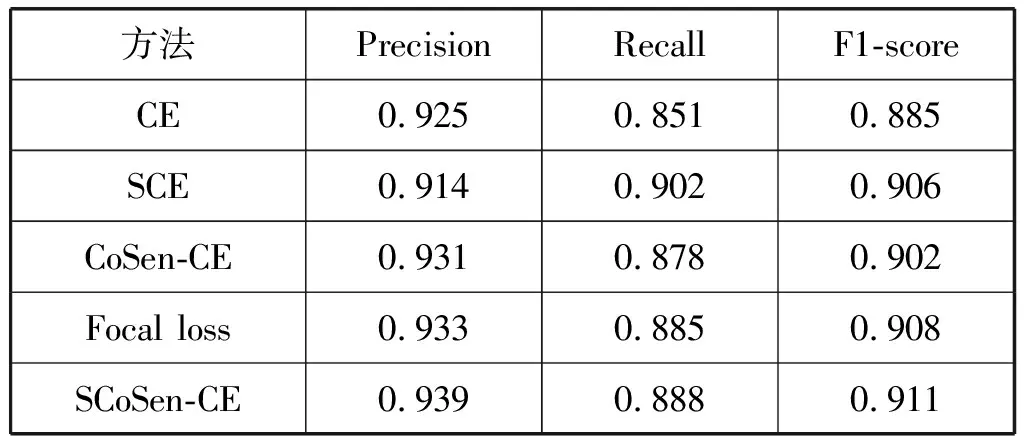
表2 不同方法的道路提取结果对比

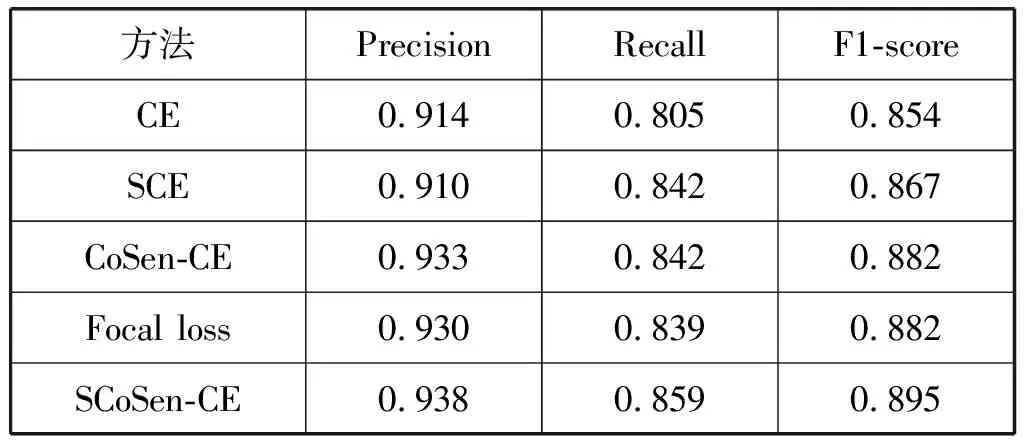
表3 不同方法的建筑物提取结果对比

由于本文方法使用基于自适应样本特征的代价敏感性的交叉熵损失函数,使得训练中的遥感影像正负样本比例更加平衡。同时在训练的过程中,根据样本的比例自适应地进行调节因子的优化,所以更加适合道路和建筑物的特征提取,从而降低了背景的学习概率,使得道路和建筑物的特征提取结果更好。从表2和表3中可以看出,在不使用代价敏感的交叉熵损失函数的情况下,VGA网络对道路检测的F1值为88.5%,对建筑物检测的F1值为85.4%,在引进SCE、CoSen-CE和Focal loss之后,使得道路的F1达到了90.6%、90.2%和90.8%,分别提高了2.1百分点、1.7百分点和2.3百分点,建筑物的F1值达到了86.7%、88.2%和88.2%,分别提高了1.3百分点、2.8百分点和2.8百分点,证明了CoSen-CE对于遥感影像中多目标检测是有效的。

引入SCoSen-CE进一步提高了对道路和建筑物网络的提取能力,使得道路和建筑物的F1值达到了91.1%和89.5%,分别提高了2.6百分点和4.1百分点,除了结果指标有所提升,道路和建筑物边缘区域预测的置信度也显著高于CE、SCE、CoSen-CE和Focal loss,证明了对损失函数的改进可以改善类不均衡带来的影响。

为了更好地体现出本文方法在细节的表现能力,使用四幅分类结果的可视化图进行对比。如图5所示,CE方法存在许多误检测区域,错误点明显多于SCE、CoSen-CE、Focal loss和SCoSen-CE。相较于对照方法,本文方法所得结果错误点较少,且道路结构和建筑物清晰完整。本文方法分辨率高,较好地保存了道路和建筑物的结构细节信息,因而能够有效避免周围背景环境干扰,准确地提取道路结构。可以看出,本文方法在结果的准确性方面优于其他方法。并且通过表4和表5可以看出,本文方法与CE、SCE、CoSen-CE和Focal loss相比有较好的提升。

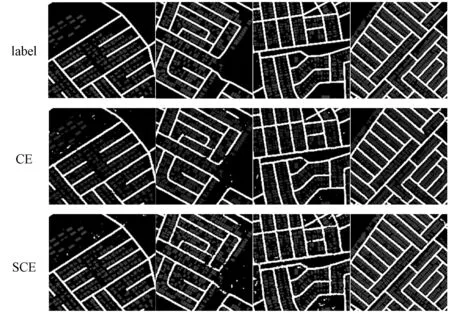
图5 道路和建筑物提取结果的可视化对比

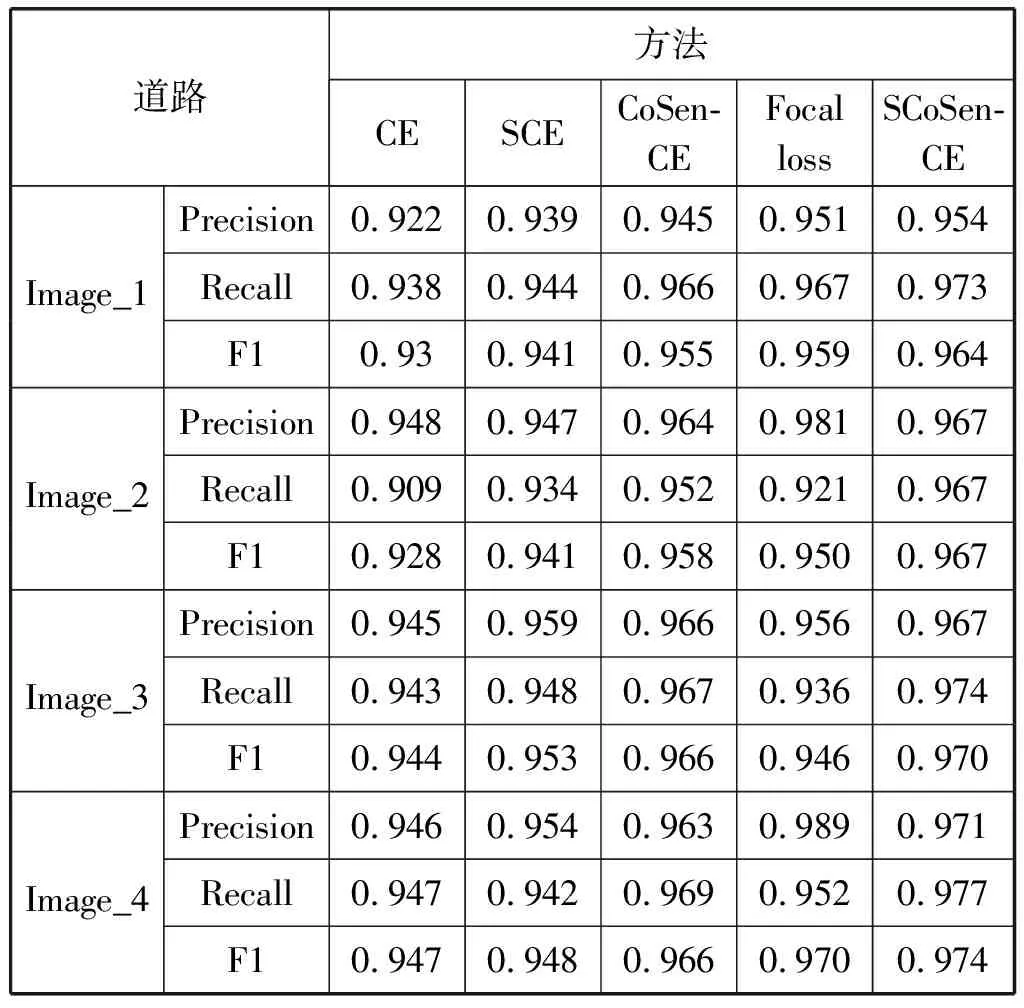
表4 可视化图中使用不同方法的道路提取结果对比

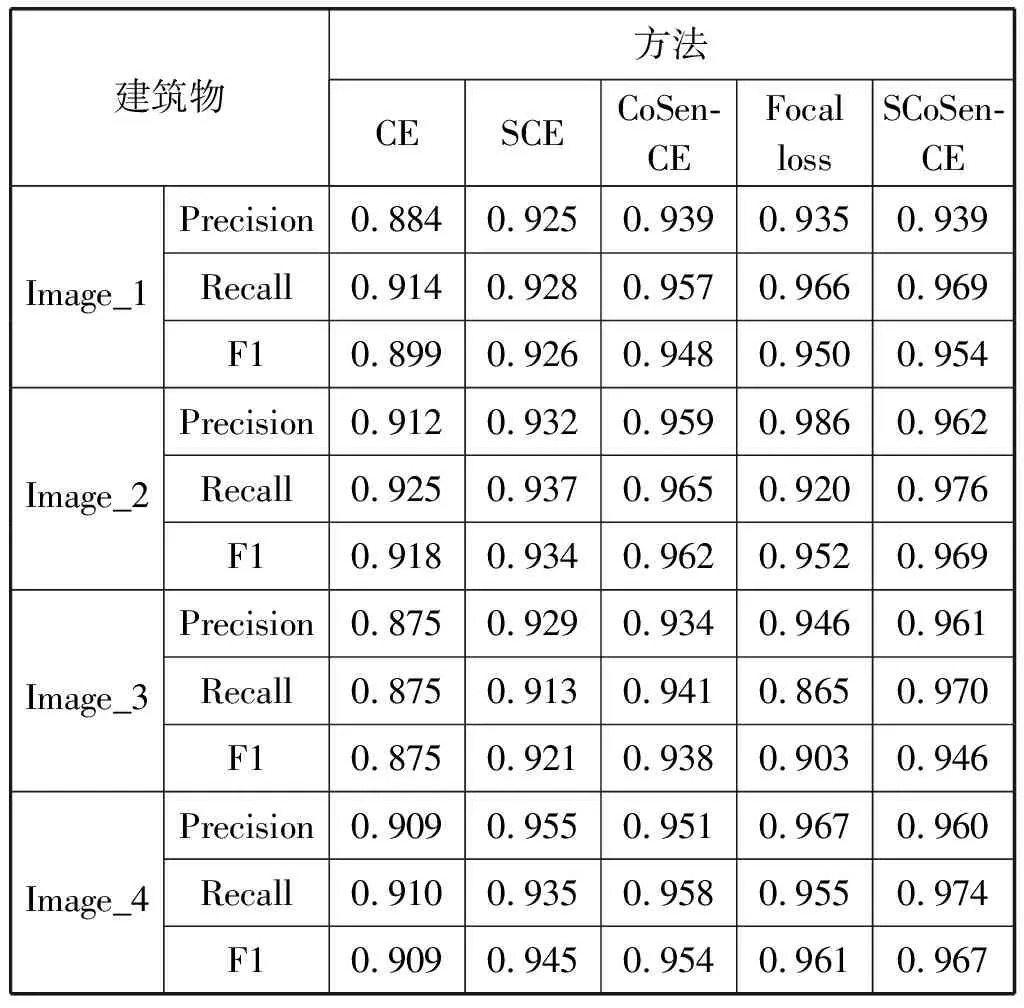
表5 可视化图中使用不同方法的建筑物提取结果对比

2.4.2P-R曲线分析

深度学习网络在应用阶段不需要预设阈值参数,为了证明本文方法具有很强的鲁棒性,在不同的情况下依然可以使用,并且具有较好提取效果,本文还使用设置阈值的方法,选取在不同阈值的情况,进行道路和建筑物的目标检测,并且对结果进行P-R曲线的绘制,如图6和图7所示。

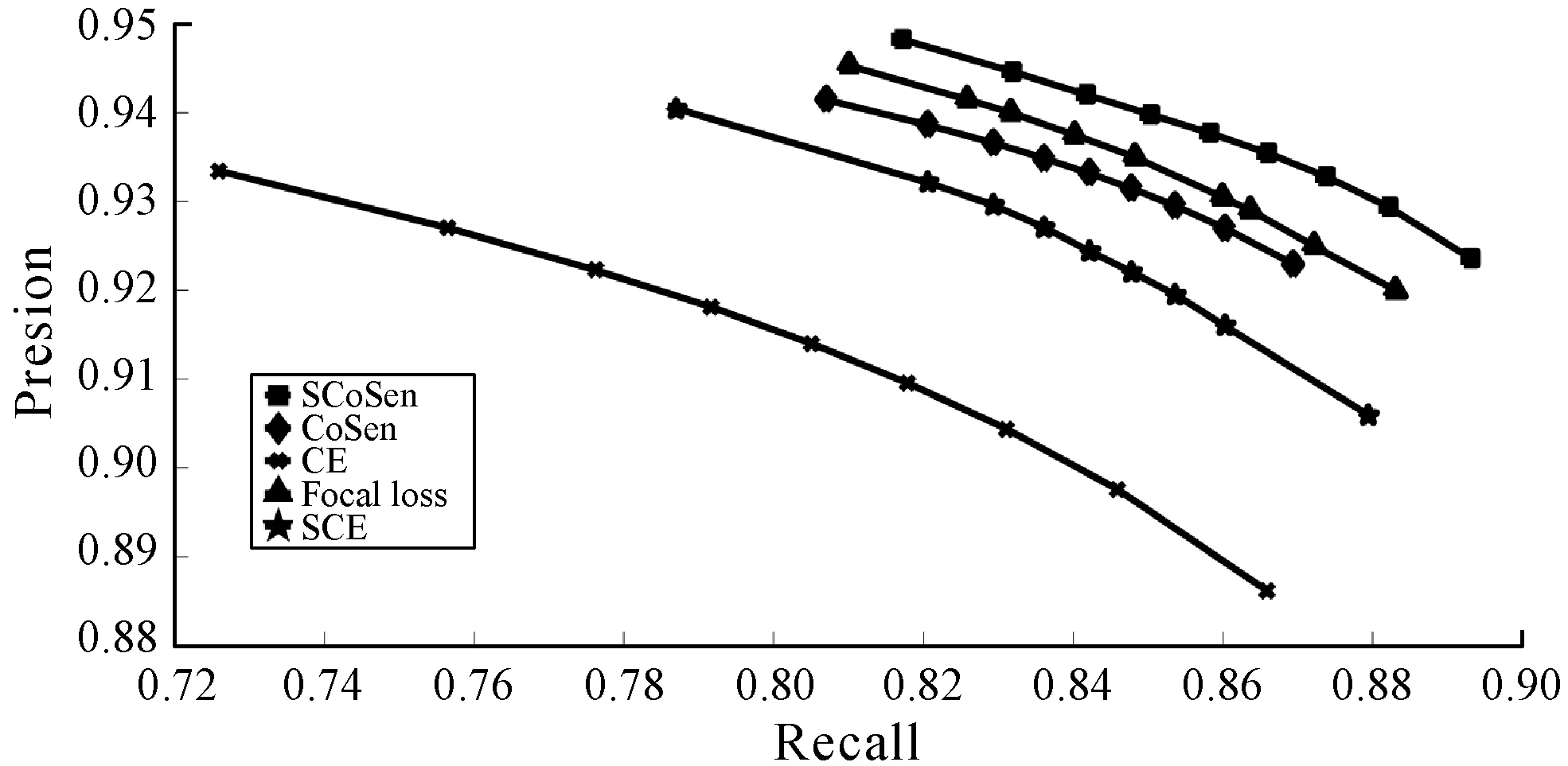
图6 建筑物不同阈值下的P-R曲线

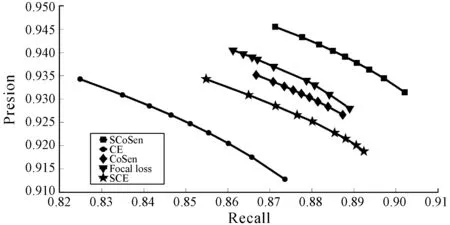
图7 道路不同阈值下的P-R曲线

其中,阈值为α=0.1,0.2,…,0.9,通过图6和图7中的P-R曲线可以看出,在不同的阈值下,SCoSen-CE的提取效果依然要优于CE、SCE、CoSen-CE和Focal loss,这也说明本文方法具有一定的鲁棒性,在不同的阈值下也能达到较好的提取效果。

3 结 语

针对遥感影像分类中数据不平衡的问题,改进交叉熵损失函数,提出适用于多分类的自适应样本特征的代价敏感交叉熵损失函数(SCoSen-CE)。为了验证该损失函数的有效性,建立类不平衡的遥感影像数据集,并且在该数据集与CE、CoSen-CE和Focal loss进行实验对比。

实验表明,SCoSen-CE在Recall、Precision和F1-score指标上均表现优异,所提取道路和建筑物结构完整清晰,且具有良好的适应性能,可以有效地解决遥感影像分类中类不平衡问题。为了验证本文方法的鲁棒性,本文还是使用预设阈值参数的方法,并通过P-R曲线表明在不同阈值的情况下,本文方法依然具有良好的性能。