统计学滤波和引导滤波相结合的点云数据降噪

霍佳欣 杨家志

(桂林理工大学信息科学与工程学院 广西 桂林 541006)

0 引 言

近年来很多学者在三维点云的数据处理领域做出了很多的贡献。三维点云数据在很多方面有广泛的应用,如3D重建、逆向工程、自动驾驶、医疗等[1-4]。激光雷达扫描是目前获取点云数据的主要方式。但由于一些人为或环境因素,以及激光雷达扫描装置本身的缺陷,通常会导致获取的三维数据带有一定的噪声,而这些噪声数据会给后续建模和测量中的相关处理带来严重的问题[5-7]。因此,三维点云滤波是建模前的关键步骤。

噪声大多数表现为高频率信息,常用的大多数去噪方法基本上都是过滤掉高频率的信息,保存低频率的信息。但是,三维点云模型中所具有的几何特征也是属于高频率信息,因此过滤除去高频率的信息有可能会错误地删除点云模型的尖锐几何特征,从而丢失特征相关的信息。而通过视觉观察物体时,对物体上所具有的特征比较敏感,所以三维点云模型数据的处理不但要去除噪声,并且也要保持三维点云数据模型特征。在分析噪声产生原因的基础上,可以将噪声进行分类,分为大尺度噪声也就是距离点云模型较远的噪声、小尺度噪声也就是距离模型较近的小尺度噪声两类,并分别进行三维点云数据处理。

点云数据处理常用的基于数学形态学滤波的算法[8]、斜率滤波[9]、TIN渐进加密算法[10]等虽然在去除点云数据模型主体上的小振幅噪声方面有很好的效果,但对于一些离群的点大多数不能通过自适应的方法去除,只能手工去除,这给点云数据去除噪声带来很多的困难。基于移动最小二乘法(MLS)的[11-12]和基于局部最优投影(LOP)的方法在去噪效果上有很好的表现,但是通常噪声点云模型的过渡平滑,从而丢失几何特征。虽然双边滤波算法[13]可以很好地保持边缘特征,但是该算法在时间上消耗较大。针对以上算法处理点云时存在的问题,本文提出一种新的去噪算法,可以把噪声进行合理的分类,分为大尺度的噪声类和小尺度的噪声类。大尺度噪声具有的特点是小而密集的点云,具有高频、大幅值等。存在于点云主体内部或者边界的散乱点,可以称之为小尺度噪声点,分别使用统计学滤波和引导滤波进行去噪。

1 算法描述

现实世界中的三维点云数据模型是包含很多特征的包括尖锐特征,如边界和角点等,很多三维点云去噪的算法对于点云模型的边界信息以及角等尖锐特征往往会被忽略,这样就会对点云的数据处理产生很大的影响。保持点云的尖锐特征的目的就是为了能够重新构造出精确的三维点云特征模型。滤波的目的是有效地平滑三维点云噪声和消除模型中的噪声,并保留物体表面原有的细节特征。算法的主要思想是先通过统计学滤波算法去除点云的大尺度噪声,保留尖锐特征,之后再通过引导滤波算法进行小尺度噪声的去除。本文算法去噪流程如图1所示。

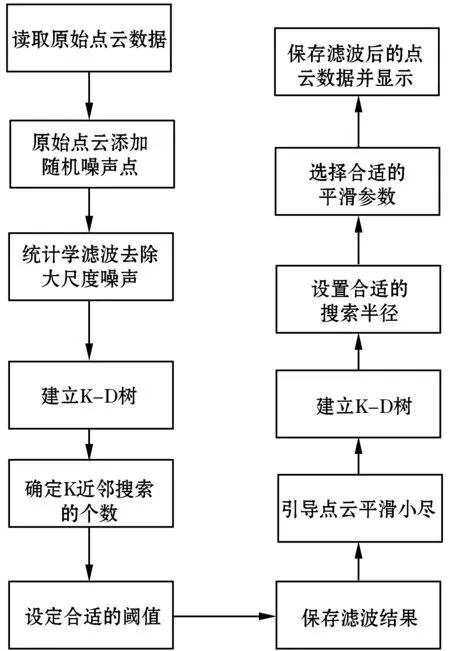
图1 点云去噪流程

1.1 算法实现关键代码说明

1.1.1统计学滤波核心代码

pcl:: StatisticalOutlierRemoval sor;

//创建去噪对象

sor.setInputCloud(cloud); //设置需要进行去噪的点云对象

sor.setMeanK(m); //设置 m 为在进行统计时考虑查询点

//邻近点数

sor.setStddevMulThresh(1.0);

//设置距离阈值,

sor.filter(*cloud_filtered);

//执行去噪计算并保存点到

//cloud_filtered

1.1.2引导滤波核心代码

pcl:: KdTreeFLANN kdtree;

//创建kd树对象

kdtree.setInputCloud(cloud);

//输入带滤波的点云数据

kdtree.setEpsilon(epsilon);

//设置滤波半径

Eigen:: Vector3d mean;

mean=neighbors_as_matrix.rowwise().mean();

//计算矩阵每行的均值

neighbors_as_matrix.transposeInPlace();

//临近点矩阵转置

Eigen:: MatrixXd centered=neighbors_as_

matrix.rowwise()-neighbors_as_matrix.colwise().mean();

//计算矩阵的中心

Eigen:: MatrixXd cov=(centered.adjoint() * centered) / double(neighbors_as_matrix.rows()-1);

//计算矩阵的协方差

Eigen:: MatrixXd e=(cov + epsilon * Eigen:: MatrixXd:: Identity(3,3));

e=e.inverse();

Eigen:: MatrixXd A=cov*e;

Eigen:: MatrixXd b=mean-A*mean;

//通过公式计算线性系数

searchPointEigenType=A*searchPointEigenType+b;

//计算滤波后的点云数据

1.2 基于统计学滤波去除大尺度噪声

激光扫描通常生成的点云数据集具有不同的密度,此外,激光扫描得到的点云数据会有稀疏的异常值产生,这是因为测量误差,从而进一步破坏点云的表达准确性,使得局部点云特征的估计复杂化,从而导致错误的估计结果,进而导致点云的高层应用表现不佳。明显离群点的特征是在空间中分布稀疏,基于离群点的特征可以认为:三维点云数据集中每个点是包括一定信息量的,越密集地分布在某个区域,则可能表示的信息量越大。噪声信息对于三维点云数据模型是属于无用信息,且包含的信息量相对来说较小,所以可以忽略不计。考虑到离群点的特征,则可以定义一个密度,某处点云密度和定义密度作比较,如果小于定义的密度,即可以称为点云无效也就是大尺度噪声。根据大尺度噪声的特点采用统计学滤波算法对此类噪声进行去噪处理。统计学滤波可以通过构建K-D树数据结构来构建KNN(k-nearest neighbor)[14],进而有效对离散点云数据进行划分和管理,加快了计算速度。对于大尺度点云统计滤波算法流程如下所示。

Step1读入存储点云数据的PCD文件,读取三维点云数据为P(p1,p2,…,pn)。

Step2对点云的数据点建立K-D树的数据结构,通过K近邻算法进行K近邻搜索。

Step3对于点云的每个点pi,定义参数K为近邻点的个数,根据K的值通过K近邻算法建立邻域,并计算点云中每个点与其最近的K个点的距离的平均值。

Step4在Step3的基础上。计算点云集中所有点的K近邻点平均距离μ和其标准差σ。

Step5式(1)中的α指的是准差倍数阈值,为确定标准范围D,设置参数μ表示为三维点云数据模型中所有点的K近邻点距离的平均值,设置参数σ表示为三维点云数据模型中所有点的K近邻点距离的标准差。一个点的距离的平均值的差值和准差倍数阈值α作比较,如果低于α,则这一点就会被划分为非噪声点进而保留,否则认为该点是噪声点进而把这个点删除。

D=μ+α×σ

(1)

Step6遍历点云数据集中的所有点,删除大尺度噪声的点云数据,保存没有删除的点云数据。

1.3 基于引导滤波去除小尺度噪声

导引图像滤波常用于图像,是由He等[21]提出的一种时间效率高的保持特征的平滑算子。算法的基本思想是将输出图像作为窗口中制导图像的线性变换。受引导图像滤波的启发,Han等[15]提出了引导点云滤波。由于考虑到三维点云数据与图像不同,图像包含强度信息,而三维点云数据不包含强度信息,直接将引导图像滤波技术的方法用到三维点云滤波不容易实现。所以从三维点云的位置信息考虑,将引导图像滤波技术扩展到点云滤波技术中形成一种通用的滤波器,为引导点云滤波。由于统计学滤波后的点云数据还有一部分小尺度噪声需要去除,引导滤波不仅能去除小尺度噪声,而且能保持点云边缘。通过点云数据建立K-D树结构对点Pi的临近点搜索可以采用K近邻搜索(KNN)或者半径搜索。

(2)

式中:N(Pi)为点pi的临近点。

Step2假设点云的局部线性模型为:

(3)

Step3通过对式(4)中点在KNN邻域的极小值进行求解,因需要对平滑效果控制进而设置参数ε为平滑参数:

(4)

Step4对函数J(ai,bi)取极小值时,对ai和bi的偏导为零。解得:

(5)

(6)

Step5由Step4中的ai、bi,可以得到pi临近点的滤波点云。

(7)

遍历所有点云,得到滤波后的点云数据并保存,平滑参数取值通常是ε<1。

该方法的主要思想是利用导引点云的邻域,将滤波后的输出点推导为导引点云对应点的线性模型。

整体去噪算法伪代码如算法1所示。

算法1整体去噪算法

输入:P(p1,p2,…,pn)。

输出:P(p1,p2,…,pn)。

//输入需要去噪的点云数据

Create KNN tree

//通过KNN来查询近邻点

For each piont i=1 to N

//对数据集中每个点遍历

Build all point K-D tree

//创建K-D树

Build all point KNN

End for

Statistic filter

For each point i=1 to N

Caculate point KNN average distance

//计算每个点临近点的平均距离

Caculate point KNN standard deviation

//计算每个点的方差

End for

Caculate all point KNN average distance μ

//计算所有点的临近点的平均距离

Caculate all point KNN standard deviation σ

//计算所有点临近点的方差

Determine the point is a noise point according to formula(1)

//通过公式(1)判断点是否为噪声点

Guided filter

Denoise the point according to section 1.2

According formula(2),(3),(4),(5),(6),(7)

OutputP(p1,p2,…,pn)

End

2 实 验

2.1 实验环境

实验的主要数据来自斯坦福大学点云模型库[18]。选用兔子模型,对点云数据添加随机噪声。计算机CPU为Intel(R)Core(TM)i5-3317UCPU@1.70 GHz,8 GB内存; 操作系统为 Windows 10 64位; 编程环境为Visual Studio 2017+Point Cloud Library(PCL) 1.8.0。

2.2 实验参数设置

带噪声的点云数据,通过统计学滤波算法去噪,此算法去除离群噪声需要选择合适的参数,图2是不同参数下的去噪结果对比,α表示标准差倍数阈值,点云数据的不同临近点个数通过设置参数K表示,取不同值消除点的个数。先确定参数α的值,因为如果α的值过小会导致部分离群点去除,如果α值过大又会使数据模型原本的数据去除。可以看出当α=1、K=20时较α=2、K=20和α=3、K=20去噪效果好,所以α=1是合适的参数。接下来确定参数K的值,α=1、K=20较α=1、K=30,α=1、K=40,α=1、K=50的去噪效果好,所以在统计学滤波去除大尺度噪声参数时,合适的参数是α=1、K=20。在统计学滤波的基础上选择合适的引导滤波参数,通过实验可以得出在进行引导滤波时,选择半径r=0.01、ε=0.1的参数值去噪效果表现最好,因为如果平滑参数过大会导致数据模型过度平滑,失去模型原有的几何特征。

图2 不同参数去噪对比

表1为带噪声的点云数据通过统计学滤波选择不同的参数得出的结果,由噪点数的多少从而判断合适的α与K的值,通过观察当α=1、K=20时去除噪声点数更多。综上所述,α=1、K=20是统计学滤波最适合参数取值。

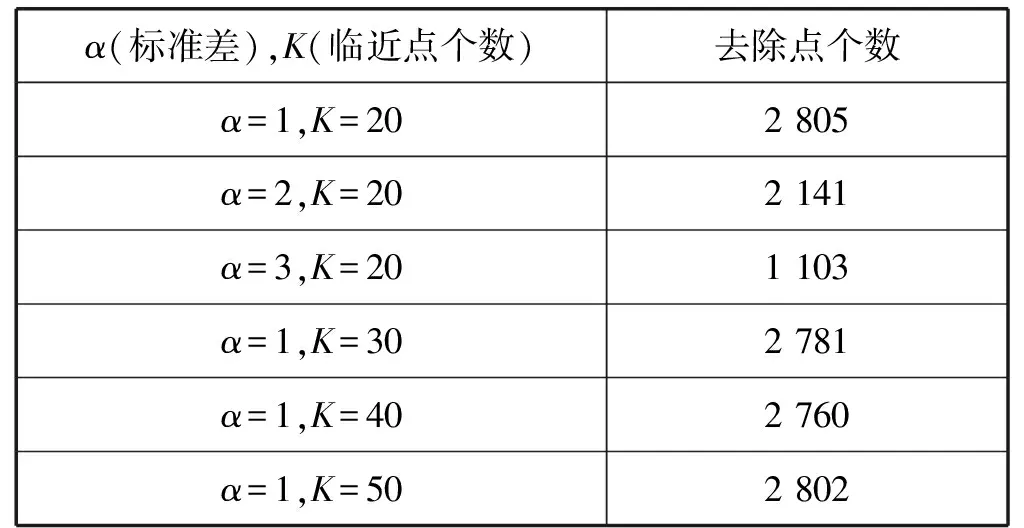
表1 不同参数去噪点的个数

2.3 实验结果及分析

兔子的点云模型数据点个数为35 947,原始点云模型如图3(a)所示,可以看出模型周围是没有噪声点的,在原始点云模型上加上3 000个随机噪声点,加噪声之后点云数据点的个数为38 947,如图3(b)所示。采用统计学方法之后可以明显看出点云的离群点基本上被去除,还存在部分小尺度噪声在兔子模型内部,如图3(c)所示;通过体素化网格滤波,兔子模型周围还存在较多大尺度噪声,如图3(d)所示;半径滤波算法虽然去除了点云模型的大部分大尺度噪声,但是兔子模型周围还有小部分大尺度噪声,如图3(e)所示。本文算法兔子周围大尺度噪声基本上被去除,小尺度噪声也被平滑,如图3(e)所示,可以看出本文算法去噪效果较好,兔子模型的噪声点基本上被去除。

为了验证本文算法的去噪效果,在Bunny模型上与体素网格滤波算法[16]、半径滤波算法[17]进行了比较,其中体素网格算法和半径滤波算法在点云库(PCL)版本1.8.0中提供,通过C++实现。

通过表2算法的运行结果可知,本文算法噪声滤除率要比体素网格滤波算法提升45.5百分点,比半径滤波算法提升了6.7百分点,表明本文算法具有较好的去噪效果。

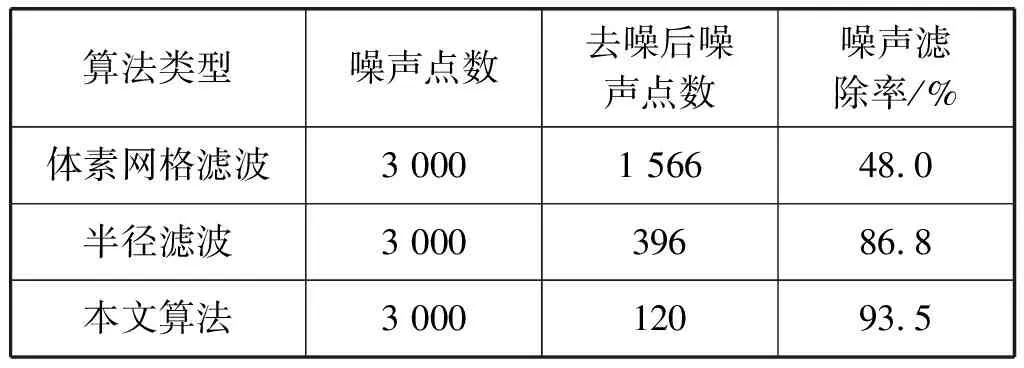
表2 算法性能比较

3 结 语

本文将统计学滤波算法和引导滤波方法相结合,应用于三维点云数据的去噪。对于两类噪声的去除,实验结果表明统计学滤波去除大尺度噪声有很好的表现,引导点云滤波在去除小尺度噪声上面也有很好的表现。所以本文算法在去除大尺度噪声的同时也去除了小尺度噪声,本文算法可以有效提高噪声滤除率,并能较好地保留有效原始点云数据,可以应用于激光雷达装置采集的带噪声的点云数据通过噪声分类进行去噪。