约束聚类算法的多目标QR码定位识别方法

王 华 赵伟甫 张 爽 高金刚 刘孝峰

1(长春工业大学机电工程学院 吉林 长春 130012) 2(长春工程学院机电工程学院 吉林 长春 130012) 3(中车长春轨道客车股份有限公司工业规划发展部 吉林 长春 130062)

0 引 言

在高铁列车轮对智能选配系统中,轮对零部件的各种尺寸铭牌信息作为选配数据支持,需要将这三种零部件的信息录入选配系统中。为了快速地录入信息,可以依据其信息生成一个二维码,使用解码软件将解码到的信息存入系统中。以车轮为例,二维码上记录着车轮的型号、生产厂家、材质、轮孔和车轮直径等信息。如图1所示,将QR码贴在车轮表面上,位于车轮上方的相机拍摄包含QR码的图片,将解码出的信息上传到智能选配系统中,便于后续的轮对选配。

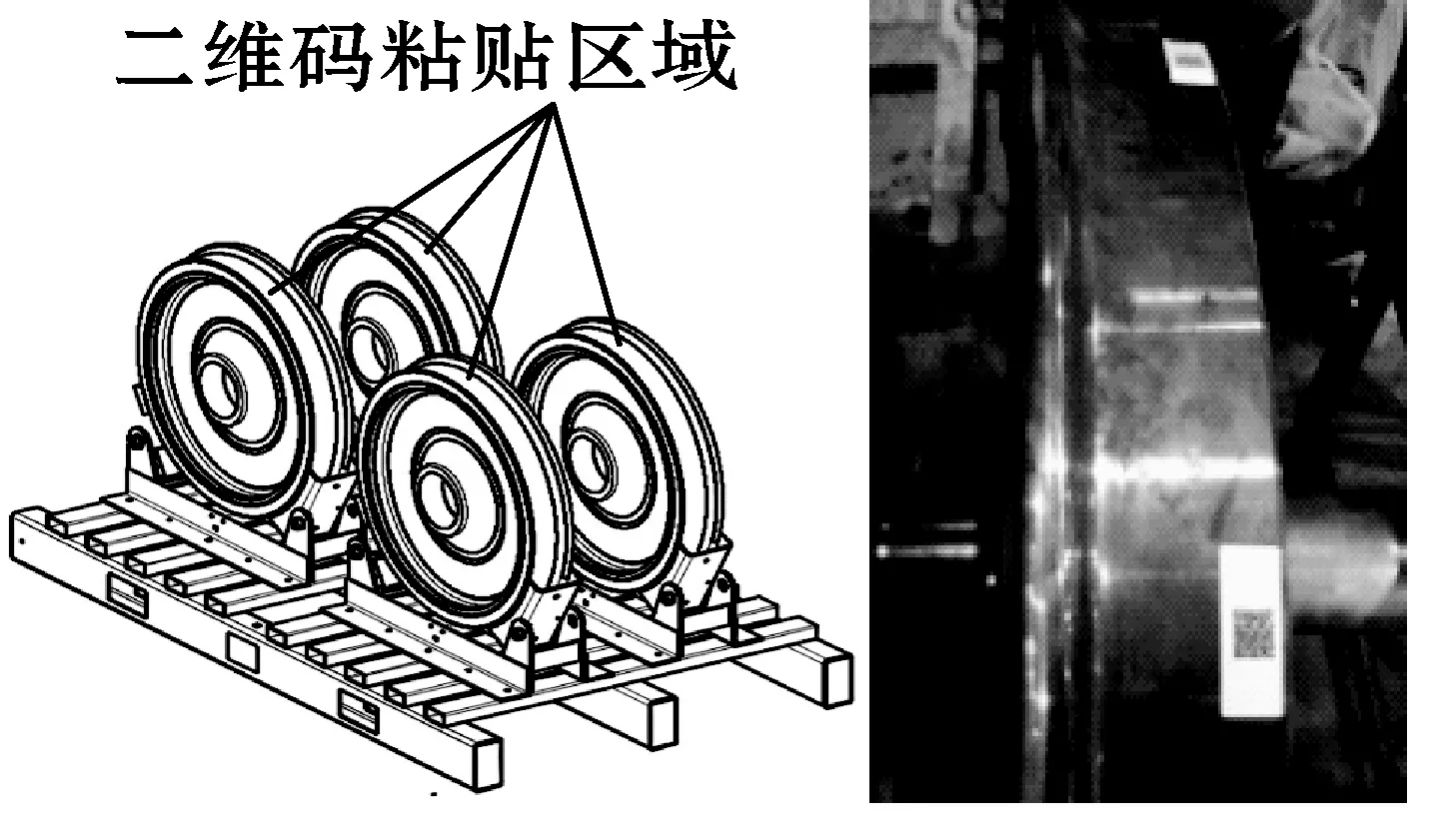
图1 粘贴位置

在日常生活中,QR码常常贴于平整位置,可以很方便获取QR码信息。在工业领域,QR码贴于曲面环境中,但是存在着多种复杂因素,对读取二维码造成了干扰。文献[1]研究了复杂背景下的DPM二维码的图像预处理,提出了自适应多阈值分割出二维码所在区域,信息保有率超过90%。文献[3]研究了一种贴于柱面的二维码生成新方法,依据二维条码和柱形条码的映射关系,对不同半径,生成了尺寸不同的二维码。从实验结论可以看出,曲率达到一定程度后条码的识别率下降,待曲率超过0.62时条码不能被识别。文献[5]研究了在距离、角度、光线、背景等不同的情况下对多个二维码提取,二维码贴于墙壁上,识别率受到上述条件的影响,在90%～98%之间。

为了解决QR码在曲面环境读取时间长,读取率不高的问题,将托盘上的所有货物对应的QR码贴到一张卡片上,只要读取到平面上多目标QR码的信息即可。基于此本文提出了多目标QR码定位识别方法,图2所示为本文算法的流程,该算法有效解决了托盘承载的货物数量和读取到的QR码数量不一致的问题,能够保证进入立体仓库的所有货物的信息全部录入智能选配系统中。

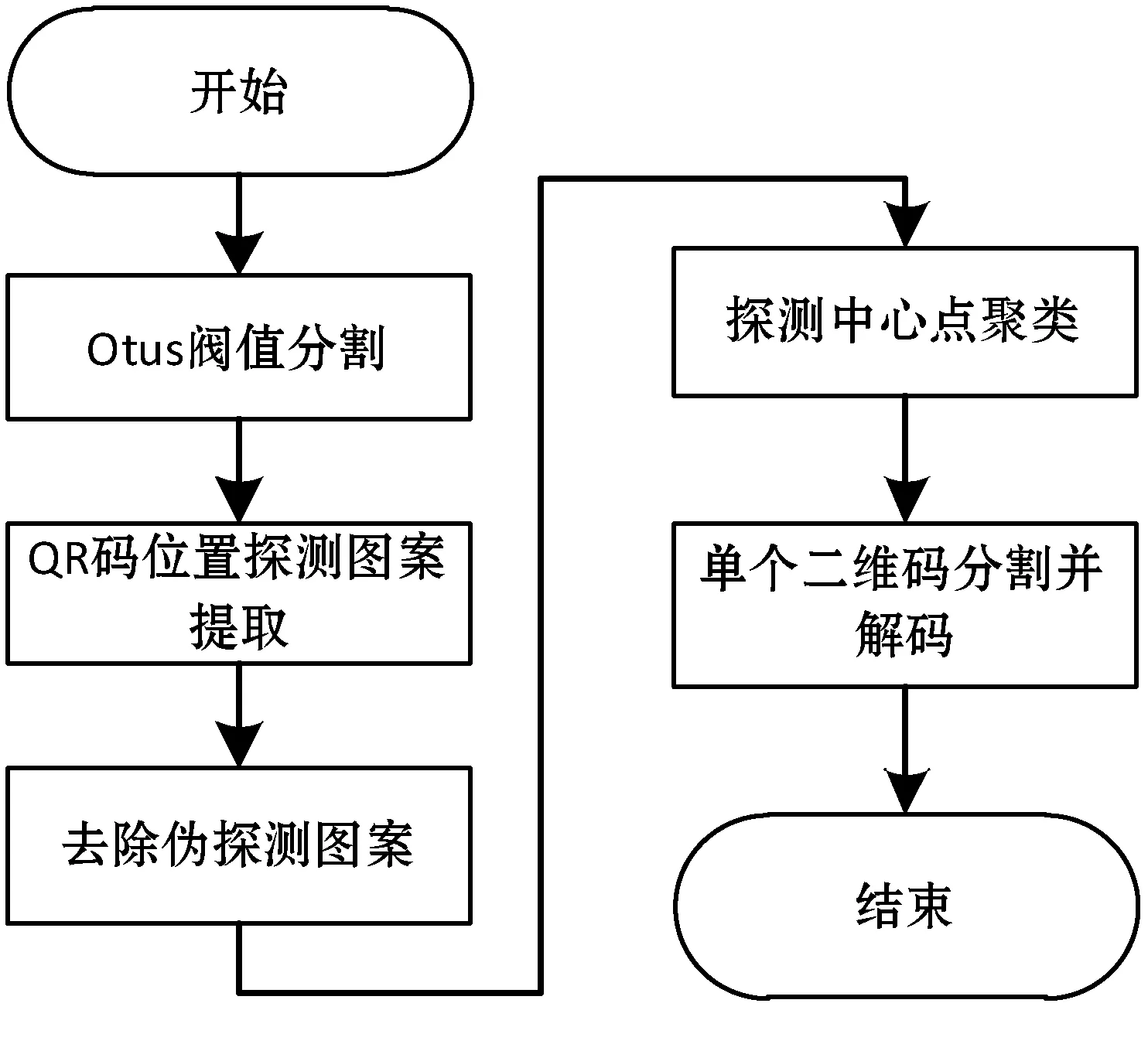
图2 算法流程

1 图像预处理

1.1 图像二值化

采用OTSU算法确定图像二值化分割阈值,图3所示为OTSU算法二值化的图像[1]。该方法又称作最大类间方差法,使得背景与前景的类间方差最大。假设前景、背景两类像素的均值为m1、m2,图像全局均值为mG。同时图像中像素被分为C1和C2类的概率分别为P1、P2。k为要求的理想灰度值[2-3],则有:

(1)

(2)

p1×m1+p2×m2=mG

(3)

p1+p2=1

(4)

类间方差表达式为:

σ2=p1(m1-mG)2+p2(m2-mG)2

(5)

对式(5)化简,可得:

σ2=p1p2(m1-m2)2

(6)

化简得:

(7)

遍历所有的灰度值i∈[0,255],使得式(7)最大的灰度值就是OTSU阈值;将大于该阈值的像素点设置为白色,小于该阈值的设置为黑色。对采集到的图片多次进行OTSU阈值处理,求出的平均灰度值128作为阈值对图像进行分割。

图3 OTSU算法二值化

1.2 QR码探测图案提取

QR码中含有3个探测定位图案,如图4所示,探测定位图案由重叠的同心的正方形组成[4],1、2、3为其在QR码图案中的位置。

图4 位置探测图案

国内外研究学者常利用背景很少出现的长度比例1∶1∶3∶1∶1旋转不变性来对QR码定位,无论从什么方向角度扫描该探测图案,该区域的长度比例是不变的。按行检测定位探测图案的步骤如图5所示,逐行扫描,比较前一像素点与后一像素点相差是否为0,将差值相同的像素点的个数放入矩阵N中,查看是否有近似满足比例的矩阵片段,将其标出。同理,按照列检测也可以得到垂直方向的满足该比例的区域[5]。

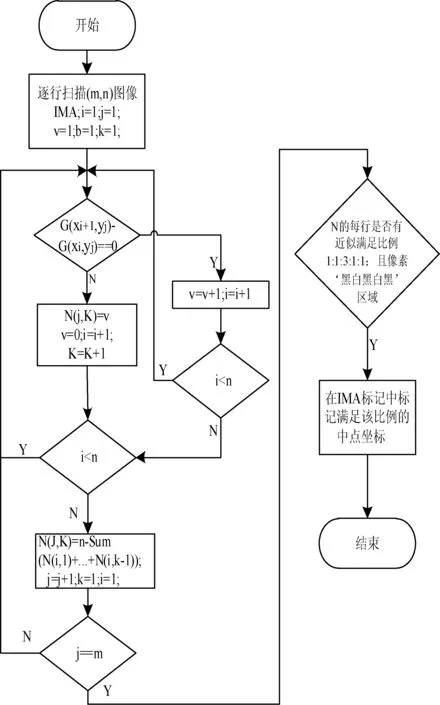
图5 定位探测图案步骤

如图6所示,以单个QR码为例,可以看到满足该比例的区域不只是位置探测图案区域,椭圆处标识QR码内部区域也存在该比例,基于此提出了去除伪探测区域算法。

图6 满足比例的区域

2 去除伪探测区域

QR Code的国际标准规定,位置探测区域与数据区由宽度为一个白色模块的分割符隔开。为了进一步确认该交点是否为位置探测区域的重心,引入了重心确认算法[6],将逐行逐列扫描后获得的中点坐标重合的点记为重心坐标,依据QR码探测图案中三块区域的面积比近似为9∶25∶49,判断的步骤[9]如图7(a)所示,去除后的重心坐标如图7(b)所示。

(a)

(b)图7 重心确认

3 位置探测图案中心点聚类

经过去除伪位置探测区域后,得到每个位置探测图案的重心坐标,其位置探测图案个数计为K,则QR码个数为K/3。需要对获取的所有坐标点进行聚类,划分出只属于同一个QR码的3个位置探测图案的重心坐标。

3.1 聚类算法

聚类思想是数据分析的核心,其核心思想是发现数据中有相同或相似属性的信息,使得这些信息分别聚为不同类别的簇,并使得相同簇中的对象之间的相似度高,而不同簇之间以及不同簇间对象的相似度低[7]。

使用传统的K-means算法是基于样本点距离初始点最小划分出不同的簇,随着迭代次数的变化,聚类算法划分的簇中各个样本点的数量、种类会有差异。而且传统的K-means算法受聚类中心的个数以及初始聚类中心坐标影响。如图8所示,每个坐标点代表位置探测图案的重心,应用聚类的思想把这些重心划分为具有QR码特征的感兴趣区域。因此,本文针对K-means聚类算法存在的缺陷,提出了新的求初始聚类中心的方法。

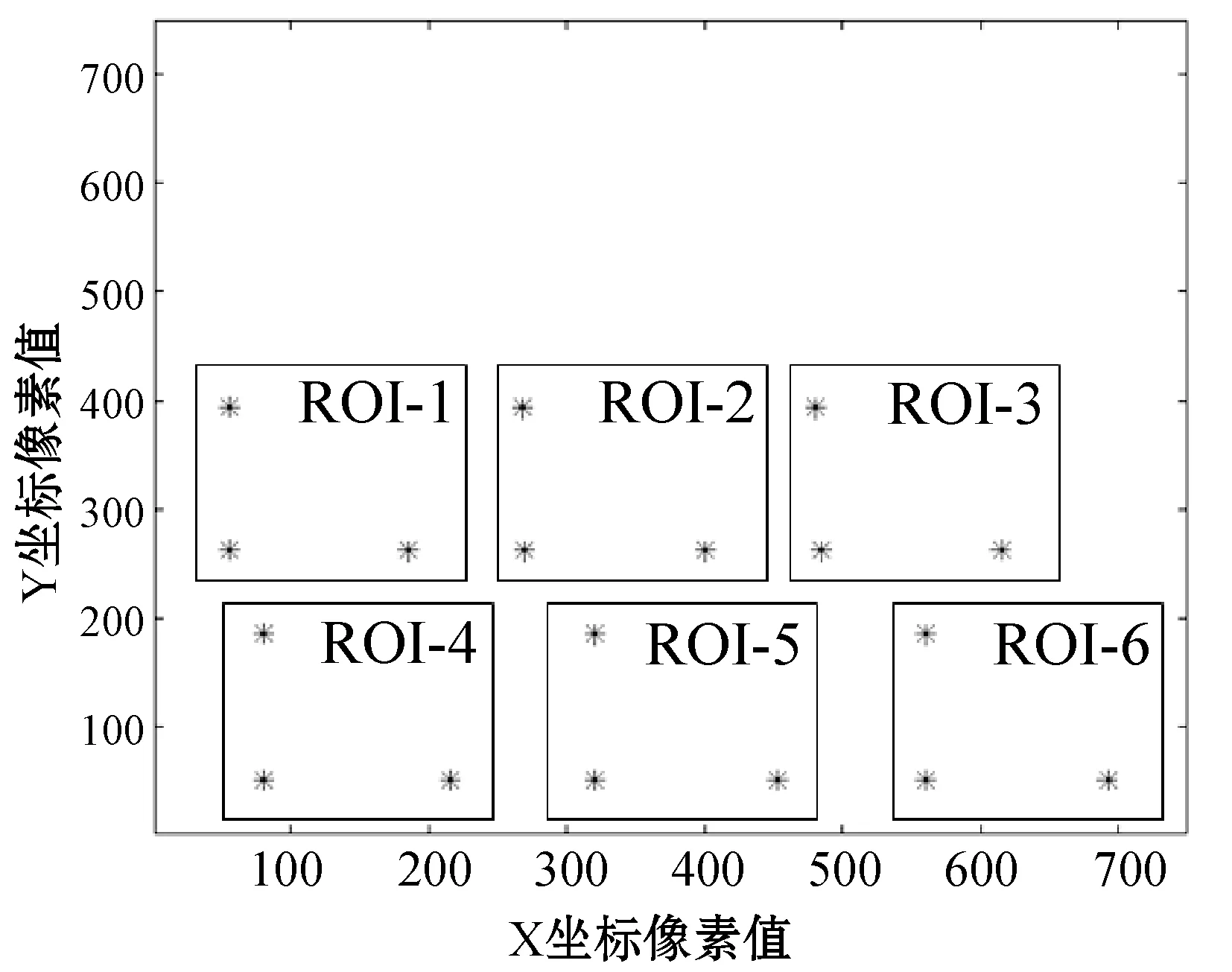
图8 理想的感兴趣区域

3.2 初始聚类中心及簇样本点选择

三个位置探测图案的重心连线近似为等腰直角三角形,考虑QR码会发生几何形变失真,对使用的QR码旋转多个角度拍摄,计算出三个探测图案重心之间的平均距离作为约束,定义直角边的约束范围在[130,135],定义斜边的约束范围在[180,185]。由此提出了基于距离约束的初始聚类中心,具体处理步骤如下:

(1) 以y=max{y1,y2,…,yn}逼近二维码区域,如果此时只有一个点与直线重合,记录该重合点与其余各点的距离和满足直角边与斜边约束范围内的两个点,开始向下搜索下一个重合点,转步骤(3);若此时有多个点与直线重合,转步骤(2)。

(2) 记录这些点的距离,将在约束范围内的点取其中一点,依据约束范围搜索第三个点,转步骤(3);若这些点的距离不在同一约束范围内,依据约束搜索各自的重心点。

(3) 将满足为一簇的移除点集,继续逼近其余二维码区域,重复上述步骤直到确定K个簇。

本文算法主要从初始点的选择以及簇的个数改进,首先簇的个数设置为K/3,然后利用直线搜索算法对初始点进行选取,按照事先定义好的距离约束对点集进行聚类,这样能够在更少的迭代次数内得到最优的聚类中心,如算法1所示。

算法1初始聚类中心选择算法

输入:位置探测图案中心点坐标数组X、Y。

输出:初始聚类中心点。

1．While(length(X)!=0)

2． y=max{y1,y2,y3,…}

//直线方程

3． m=find(Y==y)

//索引

4． n=length(m)

//数量

5．for 1 to n:

//计算这几个点是否属于同簇

6． points=(X(m(n)),y);

7．endfor

8．Distance=CalculateThisDistance(points);

//计算各自的点距

9．If(Distance∉Constraint)

//不在同一簇

10．{

11．For 1 to n

12．Distance=CalculateDistanceTo(X(m(n)),y);

//统计这些点与其余点的距离

13．if(distance in self.Distance∈Constraint)

14． {

//坐标相加

15．X-Center=X(m(n))+X.searched_point_

first+X.searched_point_second;

16．Y-Center=y+Y.searched_point_first+

Y.searched_point_second;

17． }

18． RemoveThisPoints();

19．endfor

20．}

21．Else(Distance∈Constraint)

22．{

//假设有两个点X(m(n)),X(m(n-1))在同一约束范围内;

23． Distance=

CalculateDistanceTo(X(m(n)),y,X(m(n-1)),y);

24．if(distance in self.Distance∈Constraint)

25． {

26．X-Center=X(m(n))+X(m(n-1))+

X.searched_point_first;

27．Y-Center=2y+Y.searched_point_first;

28． }

29． RemoveThisPoints();

30．}

31．endwhile

3.3 K-means聚类算法

每一簇中a(x1,y2)、b(x2,y2)和c(x3,y3)三个成员坐标,通过式(8)求出其质心坐标μ1(x,y)作为初始点。

x=x1+x2+x3/3

y=y1+y2+y3/3

(8)

求出K个质心坐标,将其作为新的聚类中心进行聚类。具体步骤如下:

(1) 将距离某个聚类中心距离近的3个样本点归类到该聚类中心,将样本全部归类完毕后得到K个簇。

(2) 计算每个簇的质心作为新的聚类中心。

(3) 重复步骤(1)和步骤(2),通过式(9)计算出此时的损失函数,直到损失函数趋于稳定值。损失函数定义为K个簇中每个样本点到其质心的平方和。实验表明,迭代10次后,若e不改变,说明聚类中心不在大范围移动。如图9所示,矩形方块内的中心点坐标即为求出的聚类中心点。

(9)

式中:k是聚类中心的个数;x是第i个聚类样本中的点;Ci是第i个聚类样本中的点的集合;μi是第i聚类样本的聚类中心点。

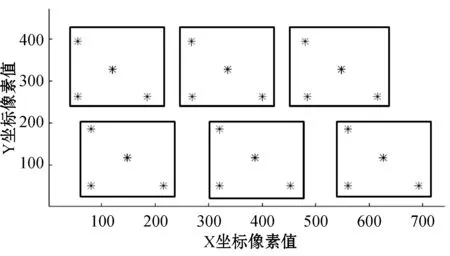
图9 聚类中心点

3.4 单个QR码分割

以单个QR码的三个位置探测图案的重心为参考点,向外扩10个单位模块宽度U,以此从多目标QR码中分割出多幅单QR码图像。 使用的QR码的位置探测图案是由7×7模块组成的,其模块宽度通过式(10)求出[8]。

(10)

式中:S为位置探测图案面积;U为模块宽度。

4 实验结果与分析

为验证本文算法流程,使用某轨道交通企业提供的10 mm×10 mm,12 mm×12 mm,15 mm×15 mm的二维码进行测试,将同一尺寸的二维码贴在一张卡片上,1 628像素×1 236像素的工业相机位于其上方拍摄,10 mm×10 mm测试样张如图10所示。对测试样张进行上述处理,并使用Zxing对分割出的QR码进行解码。

图10 测试样张

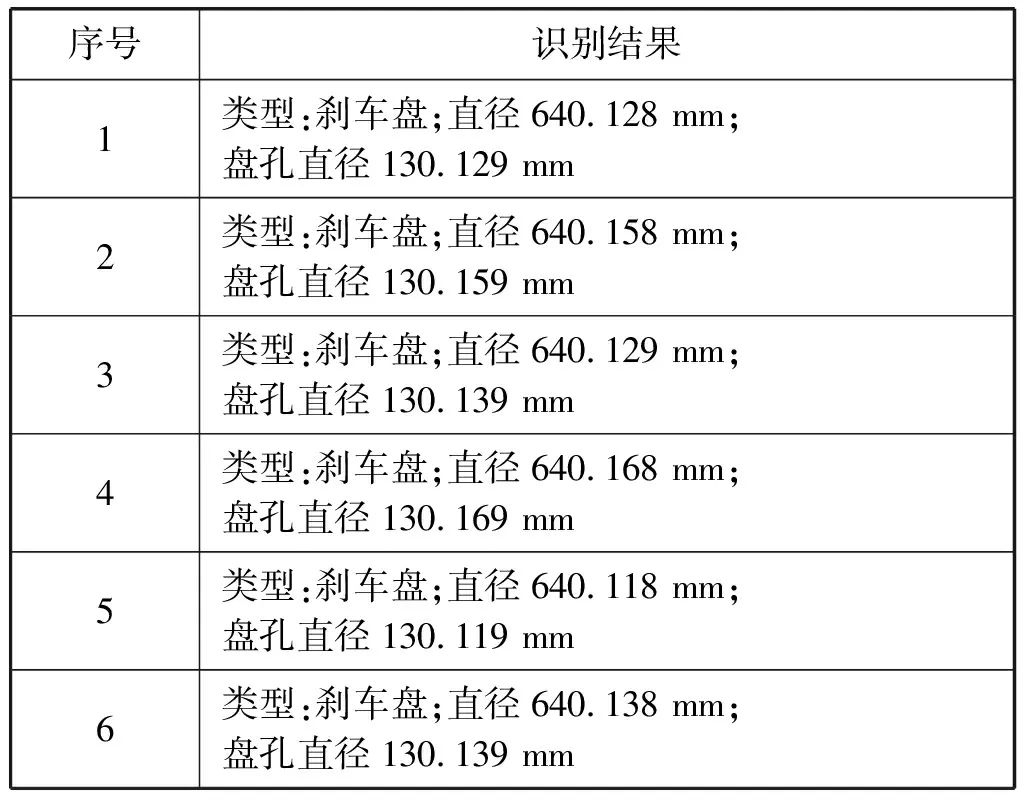
表1 二维码识别结果

实验表明,采用平面上多个QR码一起识别,其准确率相比于在曲面上识别QR码识别率要高。而且对不同尺寸的二维码识别结果进行分析,尺寸在12 mm×12 mm的识别效果要优于其他两种尺寸,识别率为96.7%。总体来说在采集到的100幅图像中,能够全部识别出所有二维码的副数达到96幅。测试过程中发现,有些图像中存在漏检现象的原因有:某些位置的QR码印刷模糊、二维码畸变严重等问题,将上述环境优化后,能够达到全部识别的要求。

5 结 语

本文就某轨道客车制造企业中高铁列车轮对智能选配系统使用的QR码应用情况展开了研究。针对多目标QR码定位问题,提出了以约束聚类算法为核心的定位算法,能够有效地对图像中多目标QR码进行定位与识别。

传统的聚类算法以距离最小为约束,容易受到噪声点的干扰,不但其聚类结果容易受初始聚类点的影响,而且需要事先给定聚类个数。本文提出了基于约束的初始聚类中心的选择算法,对初始点和簇数的选择进行改进。事先给定簇个数k,并以最大y值为扫描起点,逐行扫描探测图案重心,以距离约束选择该簇的点集,并且根据其点集坐标求该三点的质心坐标作为初始聚类中心,以聚类算法损失函数为参考变量,使聚类结果达到最优,从而分割出单幅二维码图像。