基于混合优化XGBoost算法的砂岩储层孔隙度预测
2023-06-07潘少伟郑泽晨雷建永王亚玲
潘少伟 郑泽晨 雷建永 王亚玲
1(西安石油大学计算机学院 陕西 西安 710065) 2(中国石油长庆油田公司第二采气厂 陕西 榆林 719000) 3(中国石油长庆油田公司勘探开发研究院 陕西 西安 710018)
0 引 言
在油田勘探开发中,地球物理测井(以下简称测井)是至关重要的一项技术环节。由测井曲线获得的储层参数在含油层预测中具有非常重要的作用[1]。油田勘探开发中测定储层参数的方法有两类:直接测定方法和间接测定方法。直接测定方法是钻井取心后通过分析化验的方式直接获取各种储层参数值,该方法获得的储层参数与其真实值非常接近,但花费昂贵且在油田应用范围较小,所以具有一定的局限性。间接测定方法是一种方便快捷且不可缺少的方法[2],它一般是由油田科研人员依据测井曲线建立经验公式或者简单的地质结构模型来解释未知地层的储层参数[3-4]。这种间接测定方法一般存在较强的主观性,不同油田之间经验公式和地质结构模型的可移植性也较差。并且由于不同测井曲线参数之间存在大量的复杂非线性关系[5],导致间接测定方法解释储层参数时产生的不确定性也较大。可见,以往的直接测定方法和间接测定方法在储层参数预测时均存在一定不足[6-7]。
机器学习是一种效率极高的数据挖掘方法,近几年飞速发展,在测井数据分析中更是获得了广泛应用。杨柳青等[8]使用深度神经网络(Deep Neural Networks,DNN)对砂岩孔隙度进行预测,发现与卷积神经网络(Convolutional Neural Networks,CNN)和BP(Back Propagation)神经网络相比,深度神经网络的目标预测值与实际值相差较小;安鹏等[9]利用LSTM(Long Short Term Memory)神经网络建立测井参数与泥质含量的非线性关系与时序关系,取得了较高的预测准确率;甘宇等[10]应用BP神经网络和决策树构建孔隙度的预测模型,结果表明BP神经网络具有更好的预测效果;宋辉等[11]提出一种将卷积神经网络与门控循环单元网络相结合的储层参数预测方法;桑凯恒等[12]先使用粗糙集简约地质属性,再使用机器学习方法构建储层参数预测的非线性模型;刘畅等[13]采用广义回归神经网络(General Regression Neural Networks,GRNN)预测致密砂岩储层的孔隙度,取得了较好效果。以上研究表明机器学习方法在通过测井数据预测储层参数领域具有非常广阔的发展空间。
XGBoost(eXtreme Gradient Boosting)算法由陈天奇等[14]于2016年提出,它建立在对极端梯度提升算法的基础之上,但具有更高的预测精度和更强的泛化能力。XGBoost算法目前被初步应用于石油工业领域:闫星宇等[15]在网格寻优的基础上,应用XGBoost算法构建致密砂岩气储层的孔隙度解释模型,结果表明网格寻优之后的XGBoost算法具有更高的预测精度;孙致学等[16]在随机搜索寻优的前提下,以支持向量机(Support Vector Machine,SVM)和XGBoost回归为基础,实现了对储层裂缝开度的准确预测。总体来看,XGBoost算法性能良好,泛化能力较强,运行效率较高,并可以使用多线程进行并行计算。但未经参数寻优的XGBoost算法对已有数据集的拟合度较低,导致其泛化能力和适应性均较差。因此,本文引入网格搜索(Grid_Search)法和粒子群(Particle Swarm Optimization,PSO)算法对XGBoost算法的超参数进行寻优,并把网格搜索法和粒子群算法寻优之后的XGBoost算法应用到我国陕北地区某油田储层孔隙度预测中,最后把网格搜索法和粒子群算法寻优之后的XGBoost模型对测试数据集的预测结果与线性回归(Linear Regression,LR)、支持向量机回归(Support Vector Regression,SVR)、随机森林(Random Forest,RF)、未经优化的XGBoost算法(XGB)和网格搜索法优化的XGBoost算法(GS-XGB)的预测结果进行对比,发现与其他机器学习方法相比,网格搜索法和粒子群算法寻优之后的XGBoost算法对孔隙度具有更高的预测精度。
1 算法设计
1.1 XGBoost算法
Friedman于2001年提出梯度提升树(Gradient Boosting Decison Tree,GBDT)算法[17],其原理是基于所有先前树,使用梯度下降法生成新树,使得目标函数靠近最小的方向。XGBoost称为极端梯度提升树,是一种树集成模型,可以用于分类和回归问题。XGBoost应用于回归问题时,先不断添加新的回归树,再通过新生成的CART树来拟合前一次模型的残差。训练出的完整模型包括K棵树,每棵树对应的结果之和作为最终的预测值[18]。
(1)
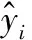
正则项的具体表达式为:
(2)
式中:γ和λ表示惩罚系数。
XGBoost的目标函数又可改写为:
(3)
式中:C为常数项。XGBoost通过不断地寻找ft来优化目标函数,目标函数进行二阶泰勒展开并且移除高阶无穷小项变成:
Ωft+C
(4)
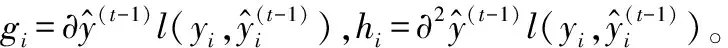
目标函数又可作进一步的化简,具体过程为:
(5)
令Gj=∑i∈Ijgj,Hj=∑i∈Ijhi,则目标函数变成:
(6)
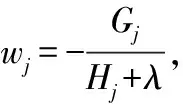
(7)
1.2 网格搜索法
网格搜索法是一种穷举遍历算法,它将所有可能的参数组合在空间中划分成若干个网格,遍历网格中所有交点,对每个参数集合应用交叉验证来计算误差,得到误差最小的为全局最优解[19]。网格搜索法可以从诸多参数中获得最优解,但是效率较低,因此本文仅使用网格搜索法确定XGBoost算法整型超参数的最优值和浮点型超参数寻优的取值范围。
1.3 粒子群算法
粒子群算法是一种随机搜索算法,由Eberhart和Kennedy于1995年提出[20]。它可以较大概率地收敛并得到全局范围的最优解。在动态的、多目标的优化问题中,相比传统优化算法,粒子群算法具有更快的搜索速度以及避免陷入局部最优的能力,可节省大量的寻优时间,并收敛至最接近的最优解。本文采用粒子群算法对XGBoost算法中的浮点型超参数进行寻优。
1.4 网格搜索法和粒子群算法寻优的XGBoost算法
本文采用网格搜索法和粒子群算法对XGBoost算法中的8个主要超参数进行寻优,这8个超参数分别是:树的最大深度(max_depth)、子节点包含实例权重的最小总和(min_child_weight)、子树的数量(n_estimators)、树的叶子节点进一步分裂所需的最小损失减少量(gamma)、训练样本的采样率(subsample)、构建树时对特征的列采样率(colsample_bytree)、权重L1正则项(alpha)和权重L2正则项(lambda)。GS-PSO-XGBoost算法的基本流程如图1所示,具体描述如下:
(1) 利用输入数据集,建立基于XGBoost算法的孔隙度预测模型。
(2) 利用网格搜索法对XGBoost算法中的max_depth、min_child_weight和n_estimators 3个整型超参数寻优,获得它们的最优值,确定gamma、subsample、colsample_bytree、alpha和lambda 5个浮点型超参数寻优的取值范围。
(3) 初始化粒子群,设置最大迭代次数。
(4) 进行训练,计算每个粒子的适应度。
(5) 迭代到一定次数时,如果整个粒子群收敛,此时gamma、subsample、colsample_bytree、alpha 和lambda 5个浮点型超参数的值即为它们的最优值;如果整个粒子群不收敛,且没有达到最大迭代次数,则返回(4)继续进行训练。
(6) 确定XGBoost算法中5个浮点型超参数的最优值,结合(2)中获得的max_depth、min_child_weight和n_estimators 3个整型超参数的最优值,形成基于XGBoost算法的孔隙度预测模型。
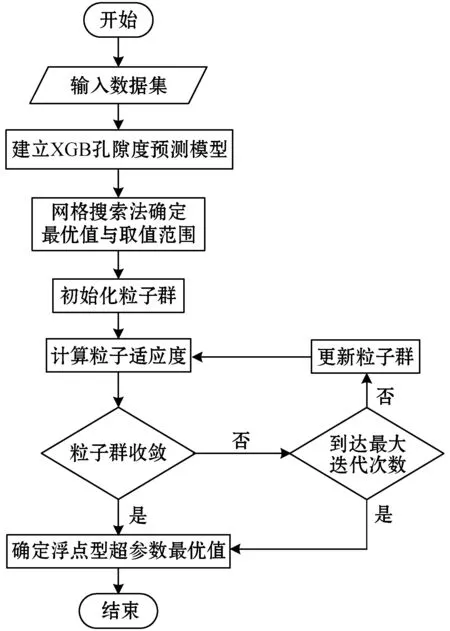
图1 GS-PSO-XGBoost算法流程
GS-PSO-XGBoost算法的伪代码如下:
算法1是关于利用网格搜索法对XGBoost算法的整型超参数寻优、浮点型超参数取值范围确定的伪代码。
算法1GS for XGBoost
Input:ai,bi,Lower and Higher bound of XGB parameter
whileeach XGB parameterdo
forXGB parameter=aitobido
find the min mae of these model
outputXGB parameter of the best model
endfor
endwhile
endprocedure1
算法2是在算法1的基础上,采用粒子群算法对XGBoost算法中5个浮点型超参数寻优的伪代码。
算法2GS+PSO for XGBoost
Input: the optimization range of PSO
foreach particleido
Initialize velocityViand positionXifor particlei
Using particles to build XGB model
Evaluate particle i and setpBesti=Xi
endfor
gBest=min{pBesti}
whilenot stopdo
fori=1 toNdo
Update the velocity and position of particle i
Using particles to build XGB model
Evaluate particle i
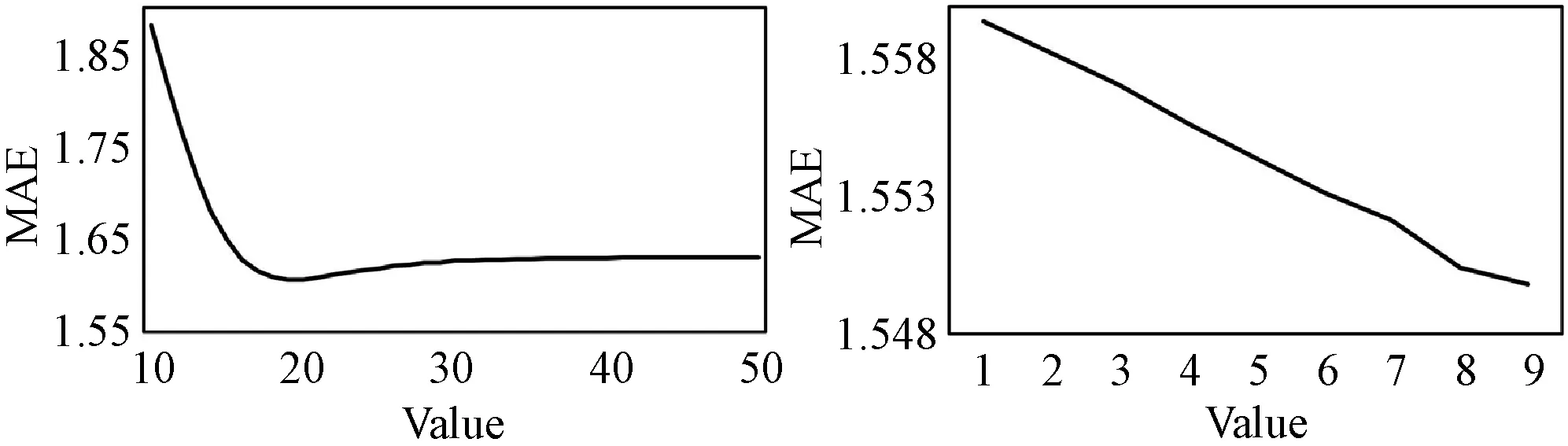
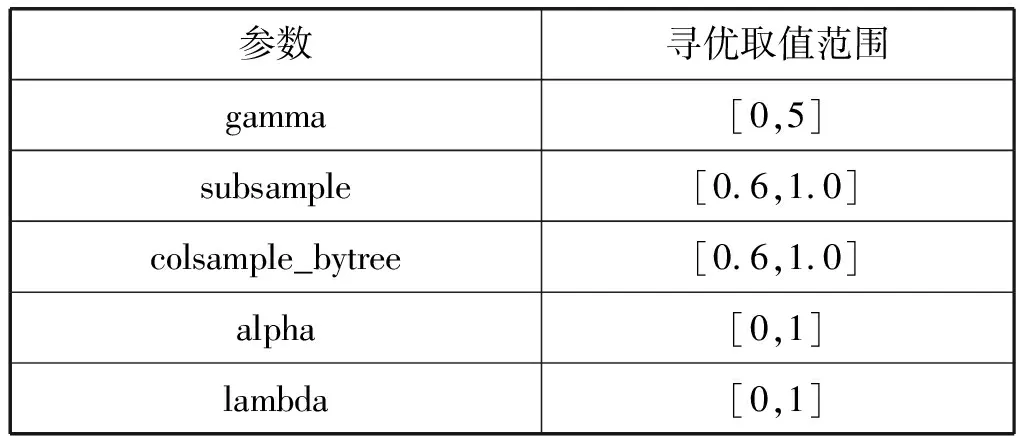
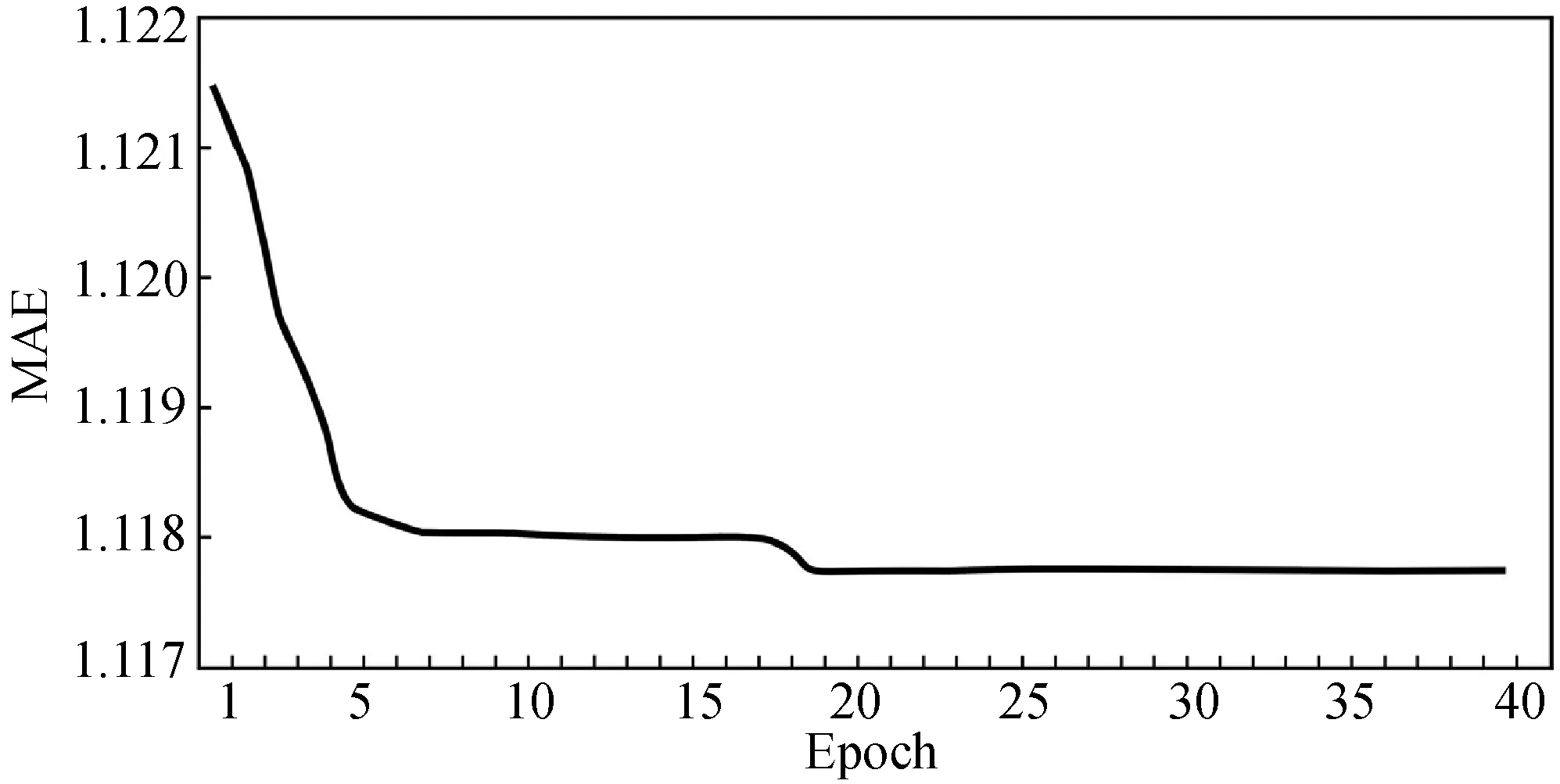
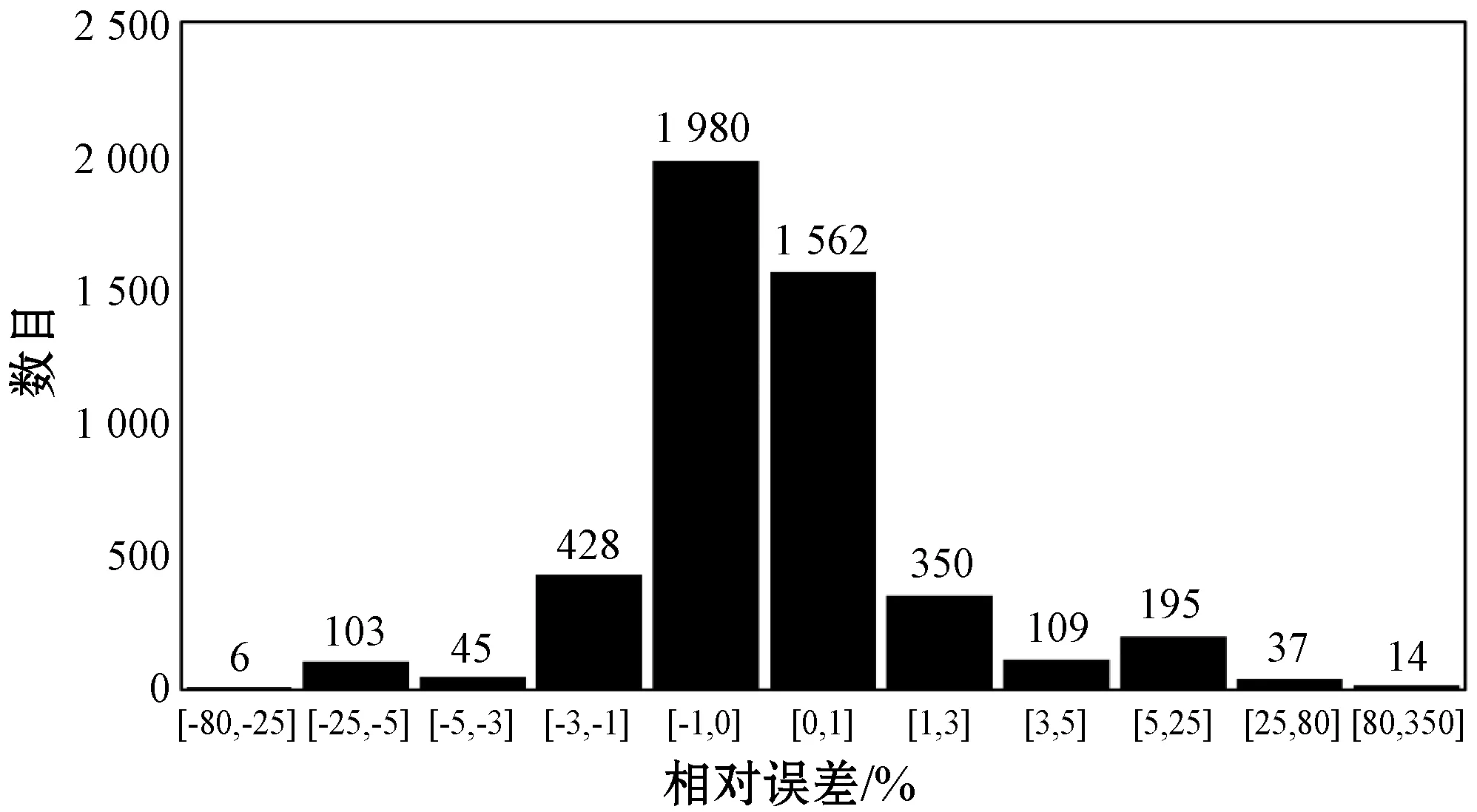
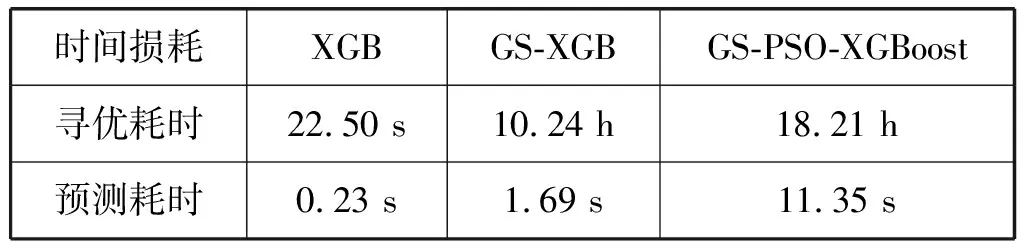
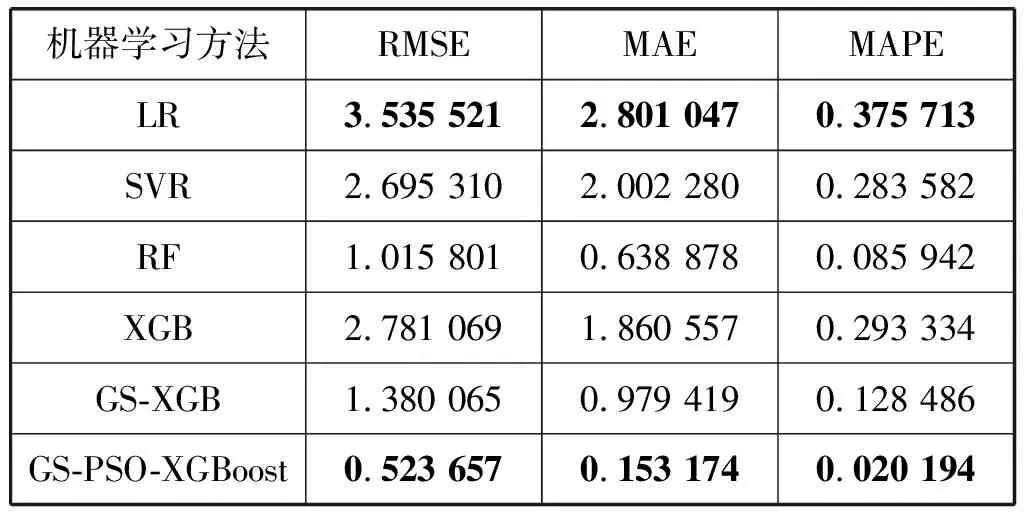
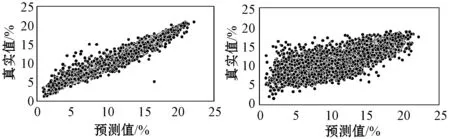
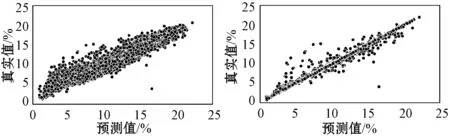
iffit(Xi) thenpBesti=Xi iffit(pBesti) thengBest=pBesti endfor endwhile outputgBest endprocedure2 本文数据集来自我国陕北地区某油田的取心井。该油田综合地质研究表明:声波时差、井径、补偿中子、补偿密度、自然伽马和阵列感应电阻率6种测井参数均与孔隙度具有相关性。为了使所建立的孔隙度预测模型在该油田具有较好的适应性和普及性,把该油田内全部取心井已有数据的顺序打乱,重新随机排列组合,形成新的数据集。训练数据集共35 066组,测试数据集共4 829组,每一组数据的采样间隔为0.125 m。数据集的格式见表1。 表1 构建孔隙度预测模型的数据集 表1中,第一列数据是声波时差,其单位为μs/ft;第二列数据是井径,其单位为cm;第三列数据是补偿中子,它是一个百分数;第四列数据是补偿密度,其单位为g/cm3;第五列数据是自然伽马,其单位为API;第六列数据是阵列感应电阻率,其单位为Ω·m;第七列数据是孔隙度,它也是一个百分数。表1中的前六列数据都是测井参数,它们对孔隙度的影响均较大。因此,在基于GS-PSO-XGBoost算法的孔隙度预测模型中,同一深度的声波时差、井径、补偿中子、补偿密度、自然伽马和阵列感应电阻率均为输入项,处于同一深度的孔隙度则是输出项。 为检验这6种测井参数与孔隙度的相关性,制作了相关性热力图(图2)[21]。图2中,AC代表声波时差,CAL代表井径,CNL代表补偿中子,DEN代表补偿密度,GR代表自然伽马,AT90代表阵列感应电阻率,Porosities代表孔隙度。由图2可看出,声波时差、井径、补偿中子、补偿密度、自然伽马和阵列感应电阻率均与孔隙度呈现出一定的正负相关性,相关系数分别为0.45、0.059、0.092、-0.54、-0.2和-0.32,即补偿密度和声波时差与孔隙度的相关性最强,其他的测井参数次之。 图2 测井参数与孔隙度的相关性热力图 在使用多个维度的测井参数建立孔隙度预测模型时,由于不同测井参数的量纲不一致,且同一种测井参数数值间的差距较大,所以需要对测井参数进行预处理,以提高模型的准确率,减少模型的训练时间。使用标准差归一化公式完成训练数据集和测试数据集的预处理,标准差归一化公式如下所示: (8) 式中:ai和Ai分别为同一数据归一化前后的值,μ是未归一化之前数据的均值,σ是标准差。经过归一化处理后的数据符合标准的正态分布,即均值为0,标准差为1。 为了评价GS-PSO-XGBoost算法对孔隙度的预测效果,选取均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)和平均绝对百分比误差(Mean Absolute Percent Error,MAPE)作为评价指标。它们的计算公式如下: (9) (10) (11) 利用网格搜索法确定XGBoost算法中max_depth、min_child_weight和n_estimators 3个整型超参数的具体做法就是以MAE为评价指标,利用训练数据集来构建孔隙度预测的XGBoost模型。当训练过程中MAE值最小时,就获得了max_depth、min_child_weight和n_estimators的最优值。最终的结果如图3[21]所示。 (a) max_depth (b) min_child_weight (c) n_estimators图3 MAE与XGBoost整型超参数关系变化曲线图 由图3(a)可知,当训练过程中max_depth的取值为20时,XGBoost模型的MAE值最小,为1.61,之后随着max_depth的增大,MAE值也在逐渐增大,说明产生了过拟合现象;由图3(b)可知,当min_child_weight逐渐增大时,MAE值逐渐变小,但min_child_weight的过大会导致XGBoost模型的欠拟合,所以遍历范围选择得较小,最终取8作为min_child_weight的值;由图3(c)可看出,n_estimators取值为140时,XGBoost模型的MAE值最小,为1.55,之后随着n_estimators取值的增大,出现了过拟合现象。这样,通过网格搜索法获得了孔隙度预测的XGBoost模型中max_depth、min_child_weight和n_estimators 3个整型超参数的最优值,分别为20、8和140。 同样利用网格搜索法,确定了孔隙度预测的XGBoost模型中gamma、subsample、colsample_bytree、alpha和lambda 5个浮点型超参数寻优的取值范围,如表2所示。 表2 由网格搜索法确定的XGBoost模型浮点型参数的寻优范围 在通过网格搜索法确定寻优取值范围的基础上,利用粒子群算法确定孔隙度预测的XGBoost模型中5个浮点型超参数gamma、subsample、colsample_bytree、alpha和lambda的最优值。首先设置粒子的种群规模为20,迭代次数为40,之后开始训练,训练过程中XGBoost模型的MAE值随训练轮次的变化曲线如图4所示,横坐标为训练轮次,纵坐标为MAE值。可看出,随着训练轮次的增大,XGBoost模型的MAE值在逐渐减小,当训练轮次达到19时,MAE值趋向稳定,之后一直保持在1.118左右。这样训练21小时后获得了gamma、subsample、colsample_bytree、alpha和lambda最优值,分别是0、0.897 1、1.0、0.071 1和0.01。 图4 XGBoost模型MAE随训练轮次的变化曲线图 当XGBoost算法中max_depth、min_child_weight、n_estimators、gamma、subsample、colsample_bytree、alpha和lambda 8个超参数的取值分别为20、8、140、0、0.897 1、1.0、0.071 1和0.01时,即成功获得了GS-PSO-XGBoost孔隙度预测模型。利用测试数据集对该GS-PSO-XGBoost孔隙度预测模型测试,所得结果如图5所示。 图5 GS-PSO-XGBoost算法对孔隙度预测值与其真实值 相对误差统计直方图 图5中,横坐标为孔隙度预测值与其真实值相对误差统计区间,纵坐标为测试数据数目。由图5可知:在4 829组测试数据中,孔隙度预测值与真实值相对误差在区间[-1,0]的有1 980组,在区间[0,1]的有1 562组,在区间[-3,-1]的有428组,在区间[1,3]的有350组,相对误差位于区间[-5,-3]和[3,5]的分别为45组和109组;孔隙度预测值与真实值相对误差在区间[-80,-25]、[-25,-5]和[5,25]、[25,80]的分别为6组、103组和195组、37组,在区间[80,350]的为14组。经过统计发现:在4 829组测试数据中,孔隙度预测值与真实值相对误差的绝对值小于等于5%的占93%左右,大于5%的占7%左右。可见,GS-PSO-XGBoost算法产生的孔隙度预测值与其真实值非常吻合,GS-PSO-XGBoost孔隙度预测模型具有非常高的预测精度。 XGBoost模型参数优化过程的时间损耗如表3所示。由表3可看出,随着网格搜索法和粒子群算法的引入,XGBoost模型参数寻优的时间从22.50 s增加到18.21 h,时间成本大大增加;与单独网格搜索法寻优相比,时间成本增加了0.8 h。 表3 XGBoost模型的训练时间性能对比 表4是XGBoost模型参数优化前后的泛化能力对比结果。由表4可发现,GS-PSO-XGBoost孔隙度预测模型在训练集和相邻油田10余口取心井数据集上测试产生的MAE分别为1.153 307和0.153 174,均低于未经优化的XGBoost模型和网格搜索法优化的XGBoost模型产生的MAE,这表明经过参数寻优之后的XGBoost算法对数据的泛化能力有了极大的提高。 表4 优化XGBoost模型泛化能力对比 引入网格搜索法和粒子群算法寻优增加了XGBoost算法计算的时间成本,但是与未经寻优的XGBoost算法相比,其MAE下降了12倍;与网格搜索法寻优的XGBoost算法相比,其MAE下降了5倍。可见,在增加的时间成本可以接受的前提下,经过网格搜索法和粒子群算法寻优之后的XGBoost算法的泛化能力和预测准确率均有极大提高,验证了本文GS-PSO-XGBoost算法的实践可行性。 基于相同的输入输出,利用线性回归、支持向量机回归、随机森林、未经优化的XGBoost算法、网格搜索法优化的XGBoost算法构建孔隙度的预测模型,以RMSE、MAE和MAPE为评价指标,通过与GS-PSO-XGBoost算法相同的测试数据集对它们进行测试,并把测试结果与GS-PSO-XGBoost算法的测试结果进行对比,具体如表5所示。 表5 6种机器学习方法预测产生的RMSE、MAE和MAPE值 由表5可知,在上述6种机器学习方法中,线性回归预测孔隙度产生的RMSE值、MAE值和MAPE值均最大,分别为3.535 521、2.801 047和0.375 713;GS-PSO-XGBoost算法预测孔隙度产生的RMSE值、MAE值和MAPE值均最小,分别为0.523 657、0.153 174和0.020 194;其他4种机器学习方法预测孔隙度产生的RMSE值、MAE值和MAPE介于上述两种方法之间。 将线性回归、支持向量机回归、随机森林、未经优化的XGBoost算法、网格搜索法寻优的XGBoost算法和GS-PSO-XGBoost算法对孔隙度的预测值和其真实值做成交汇图,如图6所示,其中:图6(a)为线性回归对孔隙度的预测值与其真实值交汇图;图6(b)为支持向量机回归对孔隙度的预测值与其真实值交汇图;图6(c)为随机森林对孔隙度的预测值与其真实值交汇图;图6(d)为未经寻优的XGBoost算法对孔隙度的预测值与其真实值交汇图[21];图6(e)为网格搜索法寻优的XGBoost算法对孔隙度的预测值与其真实值交汇图[21];图6(f)为GS-PSO-XGBoost算法对孔隙度的预测值与其真实值交汇图。可看出,线性回归、支持向量机回归和未经优化的XGBoost算法对孔隙度的预测值与其真实值相差较大;随机森林和网格搜索法优化的XGBoost算法对孔隙度的预测值与其真实值较为吻合;GS-PSO-XGBoost算法对孔隙度的预测值与其真实值最为吻合,且图6(f)中绝大多数数据点集中分布在y=x这条直线的两侧。 (a) LR (b) SVR (c) RF (d) XGB (e) GS-XGB (f) GS-PSO-XGB图6 6种机器学习方法对孔隙度预测值与其真实值交会图 通过上述分析可以得出:本文提出的GS-PSO-XGBoost算法与线性回归、支持向量机回归这些传统机器学习方法相比,其对孔隙度的预测精度有较大提高;与未经优化的XGBoost算法和网格搜索法优化的XGBoost算法相比,其对孔隙度的预测精度也有较大改善。本文提出的GS-PSO-XGBoost算法体现出了机器学习中参数寻优的重要性。 为克服已有孔隙度预测方法中存在的不足,本文提出GS-PSO-XGBoost算法,利用其构建孔隙度预测模型。与其他孔隙度预测方法相比,本文方法解决了以往孔隙度预测中测井解释方法主观性强、推广性差,机器学习方法泛化能力不足等问题,所建立孔隙度预测模型的精度也有较大提高。 本文提出的GS-PSO-XGBoost算法对孔隙度预测具有较高的精度,同时该方法具有较强的推广性,可以快速应用到陕北地区其他油田孔隙度的预测中。该方法的提出对我国陕北地区油田乃至其他地区油田孔隙度预测模型的建立具有一定的参考意义。 本文的不足之处在于没有设计实现XGBoost并行算法,在今后的工作中,要致力于设计实现网格搜索法和粒子群算法寻优的XGBoost并行算法,以提高孔隙度预测模型的运算速度和有效性。2 基于GS-PSO-XGBoost算法的孔隙度预测研究
2.1 数据集构建
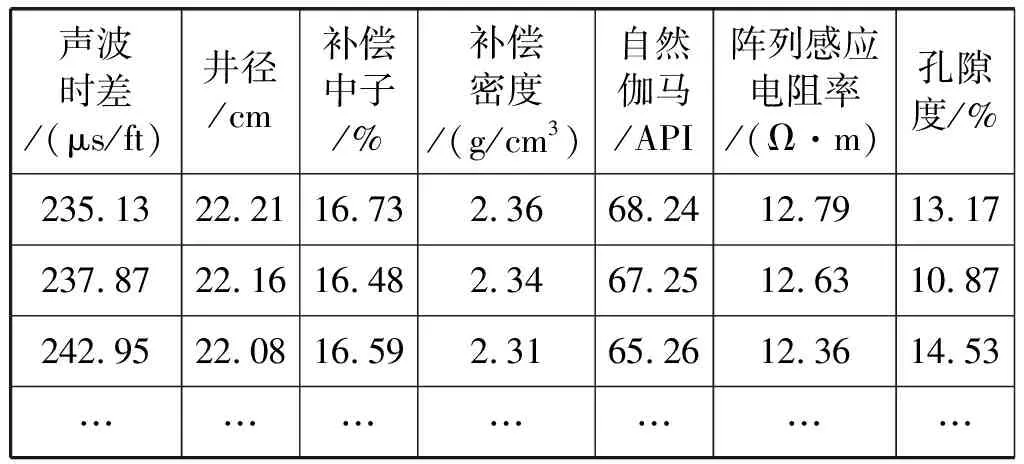

2.2 数据集预处理
2.3 评价指标
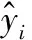
2.4 基于网格搜索法XGBoost算法的超参数寻优

2.5 基于粒子群算法XGBoost模型的浮点型超参数寻优
2.6 GS-PSO-XGBoost孔隙度预测模型的构建与检验

2.7 仿真结果分析

3 结 语
