深厚软黏土地基中大直径单桩基础现场水平受荷试验及p-y曲线适用性研究
2023-06-05鲍金虎苏静波钱荣荣
鲍金虎,苏静波,吴 锋,刘 睿,钱荣荣
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098; 2.中交上海港湾工程设计研究院有限公司,上海 200032)
海上风电作为一种绿色清洁能源,具有储能大、可持续、占用耕地面积少等优点,是诸多国家应对气候变化、节能减排的重要途径之一,也是我国推进产业转型和能源革命的重要手段[1]。与其他新能源或传统能源相比,海上风电平准化度电成本还不具备优势,严重制约了海上风电产业的良性发展[2-3]。相比于风机发电设备的研发与改进,风电基础设计优化带来的降本潜力巨大,是进一步提高海上风电项目经济性和降低海上风电项目平均能源成本的重要手段[4-5]。
由于单桩基础设备和施工技术较为完备,且承载力较高、适用范围较广,是海上风电工程的首选[6]。我国已建的海上风电场中,大部分采用单桩基础[7]。随着单机容量的不断增大,单桩基础直径也随之增大,在未来,大直径或超大直径单桩基础将是海上风力发电建设的主要趋势[8]。海上风电单桩基础在正常运营过程中会承受巨大的顶部倾覆力矩作用,水平荷载为主要的设计控制因素,所以在单桩基础设计阶段,使用高效准确的方法评估大直径单桩基础水平承载性能,从而降低单桩基础的设计成本,对控制海上风电场投资成本和实现海上风电良性发展至关重要[9]。
目前常用的单桩基础水平受荷分析方法有m法和p-y曲线。m法是一种弹性地基反力法,假设土体弹簧为线弹性,无法反映桩-土非线性作用,在桩基大变形情况下使用性较差;p-y曲线能够很好地模拟水平荷载作用下的桩-土响应特性,目前被广泛应用于单桩基础水平受荷分析中,美国API规范(geotechnical and foundation design considerations)中收录了Matlock[10]及Reese等[11]早期提出的软黏土p-y曲线计算方法并且沿用至今,随后Georgiadis等[12]根据模型试验结果提出了考虑初始刚度的双曲线形式的p-y曲线模型。国内一些学者也对p-y曲线进行了改进,王卫等[13]在考虑了桩径和地层深度情况下对黏土中p-y曲线进行了修正;朱斌等[14]基于现场大直径高桩基础实测数据,提出了相应的双曲线型p-y曲线,并分析了水平受荷大直径单桩的内力和变形;Ma等[15]通过数值分析,研究了不同桩径单桩基础土压力分布的影响以及土体的变形机理,指出通过小尺寸桩试验建立的p-y曲线对承载力的预估可能会存在误差。
欧洲针对p-y曲线的适用问题,近年来开展了PISA项目(the pile soil analysis project)研究,利用现场原型试验和数值分析,提出一套适用于欧洲海底地质情况的大直径刚性短桩设计方法[16-17],该方法考虑了单桩水平受荷情况下受到不同阻抗作用,采用圆锥函数来描述不同阻抗与桩身挠度或转角的关系。不同于欧洲紧密砂土海域中的大直径刚性短桩,我国沿海地质情况复杂,软黏土海床地基分布较为广泛[18],多数地区上覆深厚的软土层,持力层埋深较大,风电单桩基础入土深度一般较大,桩身变形呈现柔性桩或半刚性桩特征,因此有必要探究适用于我国软黏土地基大直径单桩基础的p-y曲线计算公式。
目前大多采用小直径单桩进行现场试验、实验室试验或离心模型试验,而由于全尺寸大直径单桩现场原位试验花费巨大,导致大直径单桩的现场试验数据较少,但现场试验是了解桩基在海洋条件下水平受荷响应的直接方法,能够为后续的研究与验证提供高质量的数据,从而为深入研究大直径单桩基础的设计优化奠定基础。Xu等[19]对两根2m直径钢管桩进行现场试验,并选用不同形式的p-y曲线对试桩基进行分析,发现API规范法预测挠度存在较大误差;龚维明等[20]开展海上风电基础现场水平加载试验,对API规范法、Sørensen修正的p-y曲线与实测结果进行对比;翟恩地等[21]结合响水海域2m直径钢管桩水平加载试验成果,采用m法、m折减法和API规范法进承载力计算,发现m法偏向不安全,API规范法计算结果偏保守。
本文依托某海上风电场大直径单桩基础现场静载试验,分析大直径单桩基础的水平受荷特性,并结合现场试验数据对m法、API规范法和双曲线型p-y曲线在深厚软黏土中的适用性进行对比研究,并采用有限元软件对大直径单桩基础水平承载力贡献因素进行研究。
1 工程地质及现场试桩试验方案
大直径单桩现场试验地点位于中国南部某海上风电场,该区域距离陆地最近距离约19.5km。根据区域地质及钻孔资料(图1),试验区域由海相沉积层、中砂、粉砂、砾砂和黏土等地层共同组成。海床表层的海相沉积层由层厚约13.7m的流塑性淤泥质土覆盖,下部是层厚为12.2m的粉质黏土,再下部高程-48.5~99.85m范围内依次为中砂、粉砂、角砾以及砾砂层。中间夹杂两层黏土层(层厚分别为4.8m和5.45m),两层黏土层切面光滑,局部夹中粗砂薄层,属于海陆交互相沉积。海上风电试桩所处海域的地质资料见表1,各土层根据JTS167—2012《港口工程桩基规范》中建议取m值,m为地基土基反力系统的比例系数。
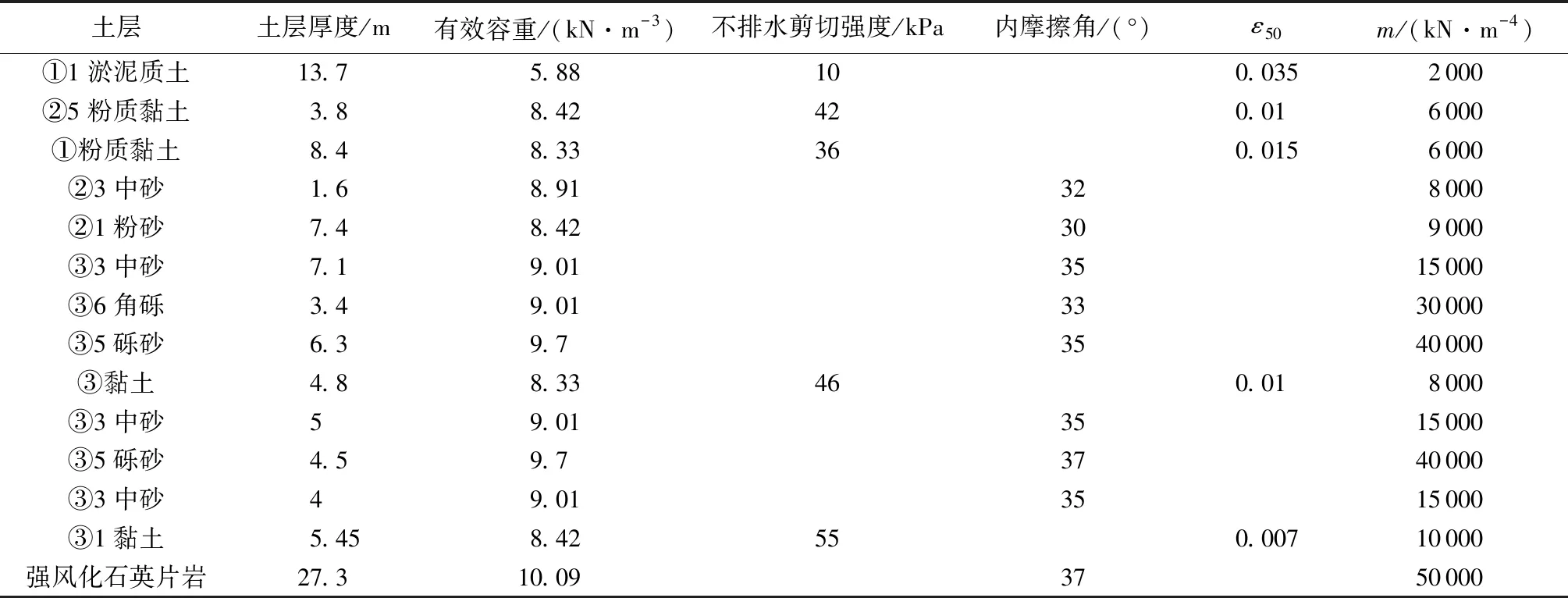
表1 试验场地土层分层及物理力学特性
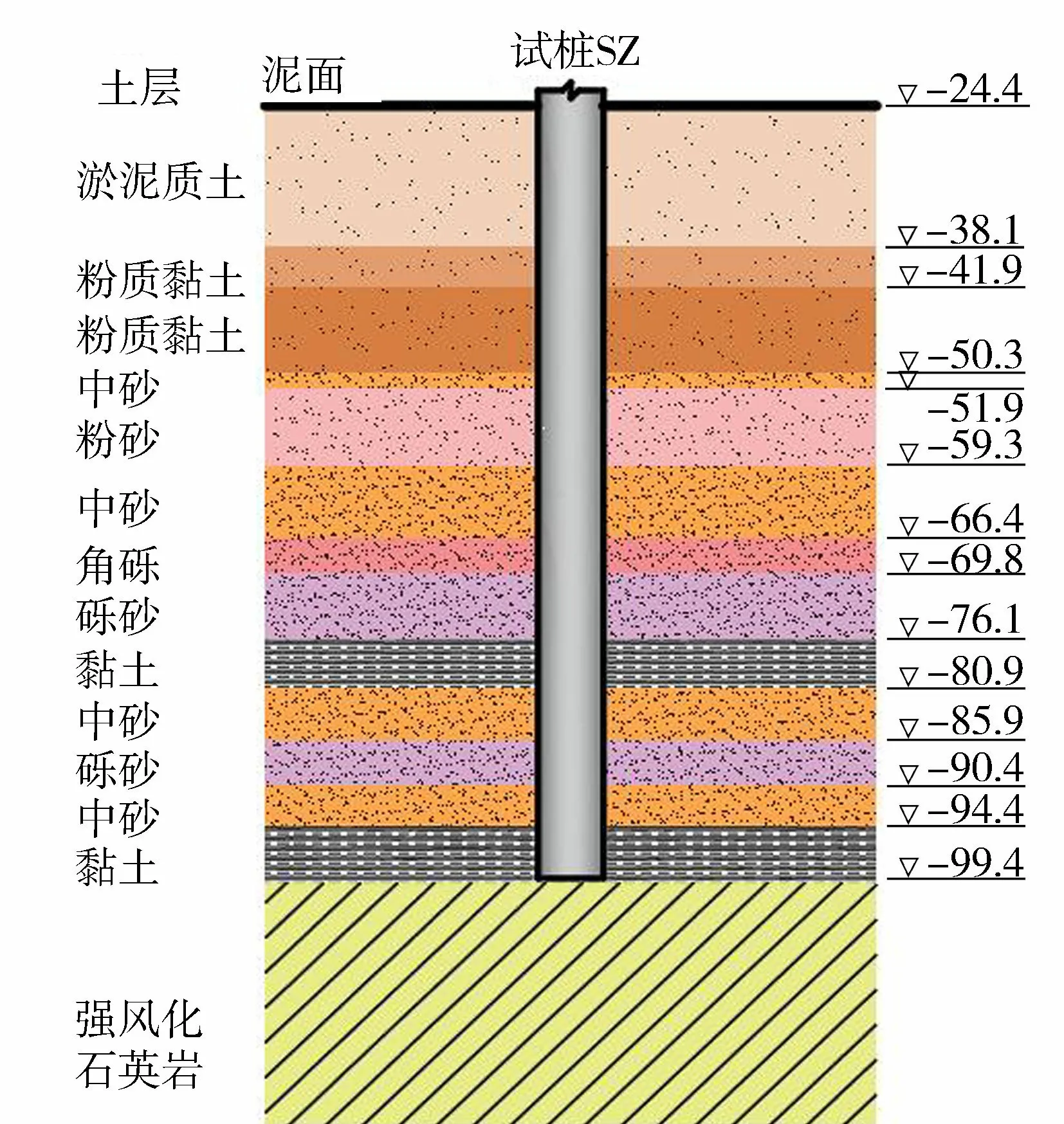
图1 试桩地质剖面(单位:m)
本次现场静载试验装置布设如图2所示,试桩对象为2.4m直径的开口钢管桩;静载试验使用了4根锚桩和2根基准桩,其中M1~M4锚桩为直径2.2m的开口钢管桩,4根锚桩为试桩提供反力;J1和J2基准桩为直径1.5m的开口钢管桩,主要用于架设基准梁。试桩、锚桩、基准桩的类型及尺寸参数如表2所示。
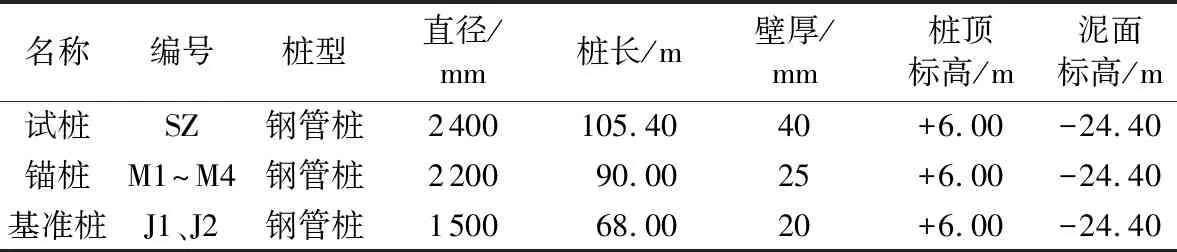
表2 现场静载试验试桩、锚桩及基准桩尺寸
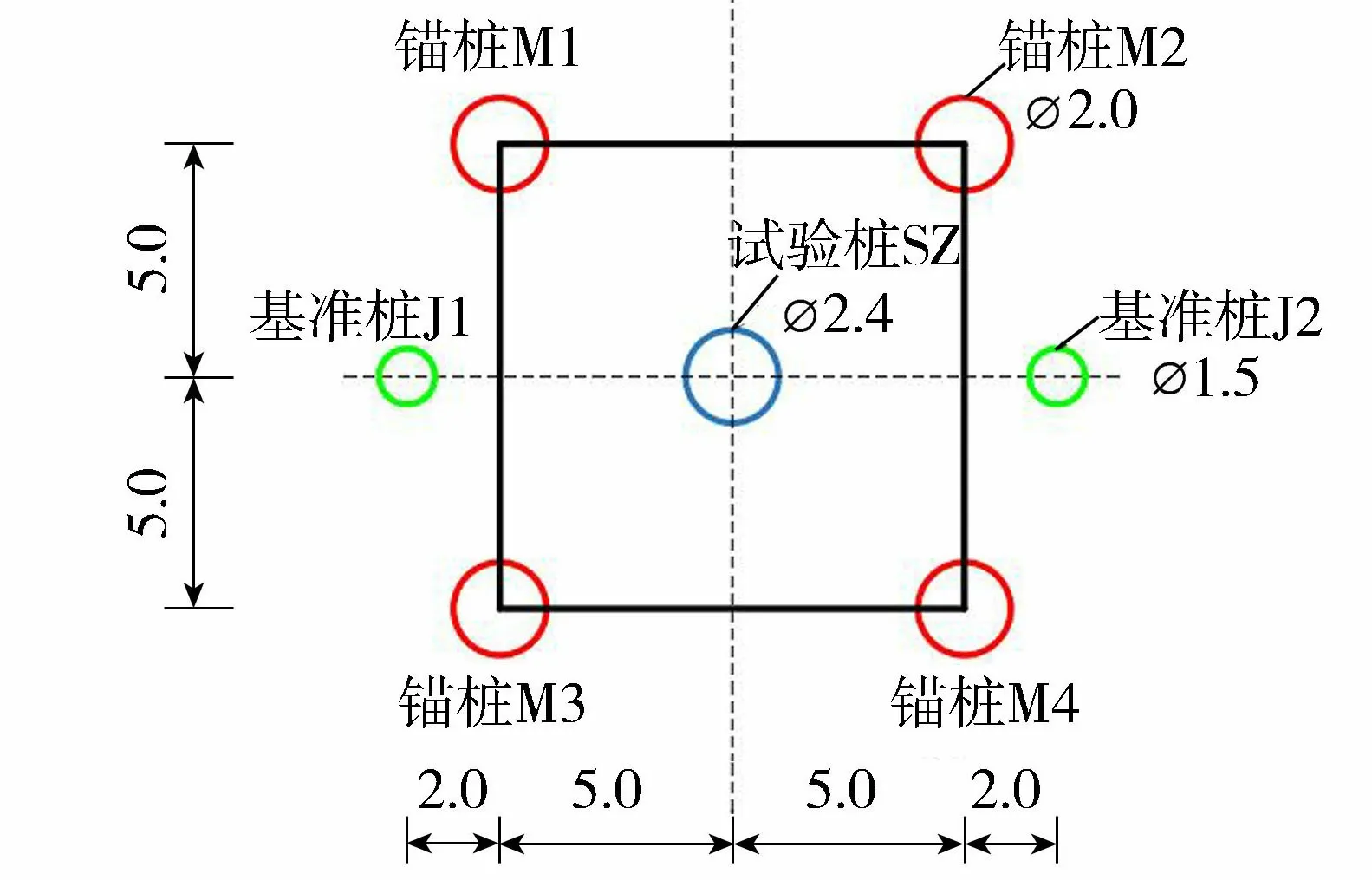
图2 现场静载试验平面布置(单位:m)
2 试桩试验过程及响应分析
根据 JTS237—2017《水运工程地基基础试验检测技术规程》对基准桩静载的试验方法、试验装置的规定,试验时,试桩桩顶位置为自由无约束状态,采用顶推法施加水平荷载,由两侧的锚桩提供试验反力。整个试验具体步骤为:单向单循环加载,试桩每级加载量按100kN控制,根据现场地质勘测情况,预估试桩最大加载量为1600kN。试桩的加载力点标高为+5.10m。
试桩在加载点处的荷载-水平位移曲线如图3所示,在水平静载试验过程中,随着水平荷载的增加,试桩的水平位移逐渐增大。随着水平荷载从100kN增加至700kN,加载段的荷载-水平位移曲线基本保持线性,可以判断单桩在水平受荷过程中处于线弹性阶段。由于荷载装置及试桩条件等限制,试桩未达到极限破坏状态。根据静载试验规范并结合试验目的,当水平荷载提升至700kN时,加载点的水平位移超过了500mm,此时加载点水平位移为537.47mm,达到试验要求。随后停止加荷,逐渐卸载至水平加载为0,此时对应的加载点残余水平位移为71.53mm。
图4为试桩在不同水平荷载作用下的实测桩身水平位移响应。可以发现随着荷载增大,桩周的浅层土体已经无法提供足够的抗力来抵抗桩身变形,此时需要逐渐调动深层土体来提供抗力,即桩身水平位移随着水平荷载的增大而增加,第一水平位移零点的深度也随着横向荷载的增加逐渐往深处偏移,由弯矩积分推导和桩身测斜两种方式得到的桩身水平位移变化规律基本一致。根据试桩桩身水平位移分布可以发现,试桩呈现明显的柔性桩工作特性,到一定深度后桩身水平位移基本没有变化,可以被看成嵌固在地基中。
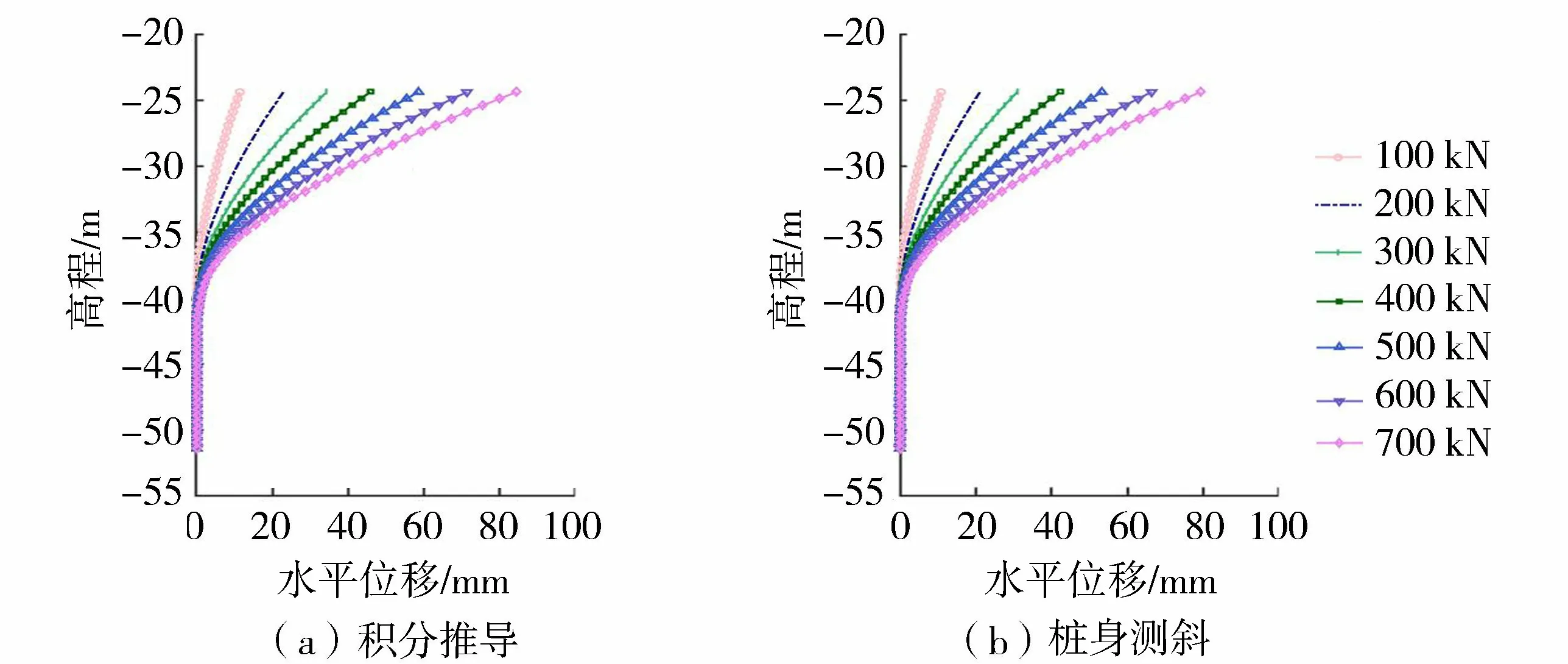
图4 不同水平荷载作用下静载试验桩身水平位移响应
图5为试桩在不同水平荷载作用下实测桩身弯矩响应。现场试验结果表明,随着水平荷载的增加,试桩的桩身弯矩也随之增大。不同荷载的最大弯矩均出现在4倍桩径深度附近。在试验最大水平荷载(700kN)作用下,桩身的最大弯矩为25676kN·m,出现在泥面以下10m处(高程-34.4m),第一弯矩零点出现泥面以下22.1m处(高程-46.5m)。
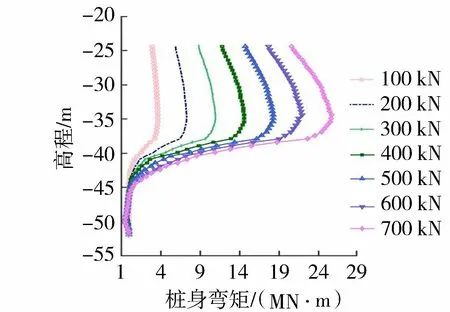
图5 不同水平荷载作用下静载试验桩身弯矩响应
3 软黏土p-y曲线适用性分析
试验单桩场地海床表层上覆13.7m流塑性淤泥质土,地基承载力较弱,而海上风电基础结构的承载力要求较高。为探究大直径单桩基础在水平荷载作用下深厚软黏土地基土体的调动情况,并为深厚软黏土地基中风电基础设计优化提供参考依据,对实测结果、m法、API规范法以及双曲线型p-y曲线进行对比。
3.1 单桩水平承载特性计算方法
3.1.1m法
m法假定地基反力系数随深度线性增加,可以采用有限元模拟或解析法求解[22]。本文采用数值方法进行模拟,将弹簧单元在桩身分段施加,弹簧水平向弹性系数取值为[23]
Ks=mBzh
(1)
其中B=0.9(D+1)
式中:B为桩计算宽度;D为桩径;z为桩在泥面下的深度;h为计算所取土弹簧间距。
3.1.2API规范法
对于软黏土地基,目前使用较多的是API规范推荐的p-y曲线计算方法,公式为
(2)
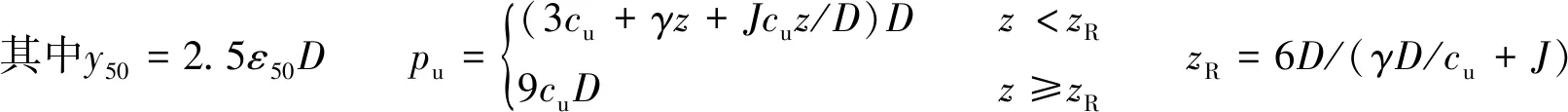
式中:pu为软黏土的极限土反力,kN/m;y为水平位移,m;y50为桩周土体在极限抗力一半时的水平变形;ε50为不排水压缩试验极限强度之半时的应变;zR为极限横向土抗力转折点的深度,m;cu为黏性土不排水抗剪强度,kPa;γ为土体有效容重,kN/m3;J为经验系数,通常取0.5。
3.1.3 双曲线型p-y曲线
朱斌等[24]指出,双曲线型p-y曲线能够较好地反映桩周土的发展趋势,并能考虑桩基的水平小变形和大变形。双曲线型p-y曲线表达式一般为[25]
(3)
其中k=ηz
式中:k为地基反力初始模量[23];z为土层位于泥面以下的深度;η为初始地基反力比例系数,可以根据m法相关规范中地基土水平抗力比例系数取值或通过现场实测获得。pu仍按照API规范法取值计算,JGJ94—2008《建筑桩基技术规范》指出,当水平力为长期荷载时应将地基反力比例系数值乘以0.4降低采用,本文在使用双曲线型p-y曲线进行计算时以该比例折减降低地基反力比例系数。
3.2 软黏土单桩p-y曲线适用性
泥面下4.5m、7m及10.5m处根据实测桩身的计算结果与API规范法和双曲线型p-y曲线计算的p-y曲线如图6所示。从图中可以看出:
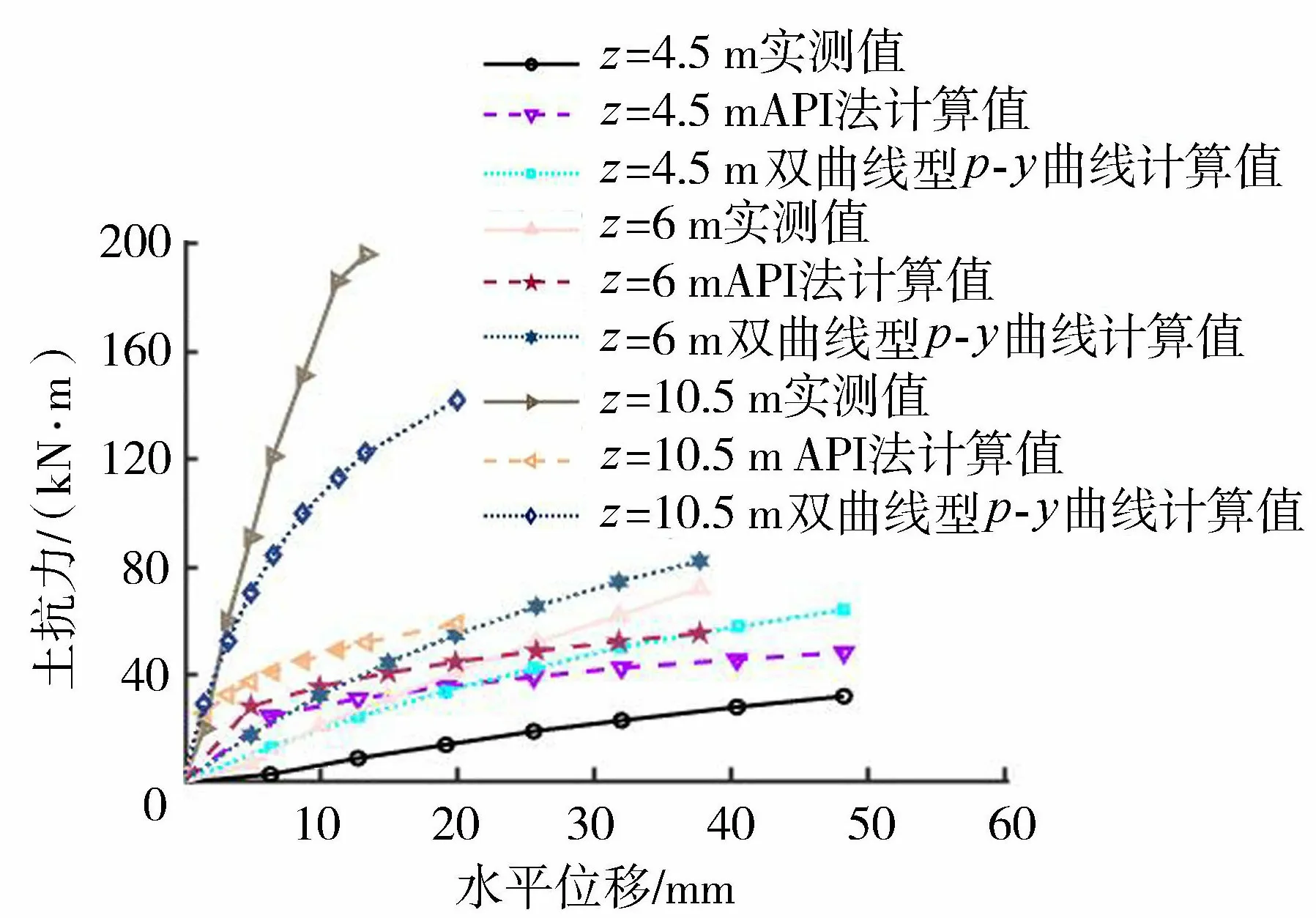
图6 软黏土中不同深度下的p-y曲线
a.浅层土体不同深度下p-y曲线土抗力也随着桩身挠度的增大而呈现线性增加,p-y曲线的初始刚度(p-y曲线线性阶段的斜率)随着深度的增加也随之增大。由于泥面以下13m范围内基本为淤泥质土,表明同一性质土体中的p-y曲线初始刚度和土体侧向应力水平密切相关。
b.在泥面下4.5m处双曲线型p-y曲线与API规范法相较实测值初始刚度以及极限土抗力偏大。
c.在泥面下7.0m处,可以看出小变形阶段API规范法初始刚度偏大,且得出的极限土抗力较实测值较小;双曲线型p-y曲线在该深度与实测值拟合较好。
d.在泥面下10.5m处双曲线型p-y曲线与实测计算结果在小变形阶段初始刚度较为一致,但其极限土抗力较小;而API规范法计算结果与实测值相差较大。综上可以看出,对于深厚软黏土地基中的水平受荷大直径桩来说,API规范法与双曲线型p-y曲线在浅层土中计算的初始刚度偏大,且API规范法严重低估了桩的极限土抗力;双曲线型p-y曲线在一定深度下与实测结果较为接近,且在泥面下较深位置,曲线的初始刚度与实测结果较为拟合,但是根据API规范法计算出的极限土抗力相较实测值偏小。
桩顶处荷载-位移曲线如图7所示。相较于实测值,在水平荷载较小时,双曲线型p-y曲线、m法与实测结果拟合较好;而随着荷载的逐渐增大,m法与双曲线型p-y曲线计算得出的水平位移较实测值偏小。这是由于m法主要应用于小变形阶段的弹性长桩,而在水平加载变形较大时,m法已不适用于估算大直径单桩水平受荷特性,考虑地基承载力比例系数,折减后的双曲线型p-y曲线与实测结果更为接近;API规范法计算所得水平位移较大,其结果偏保守。
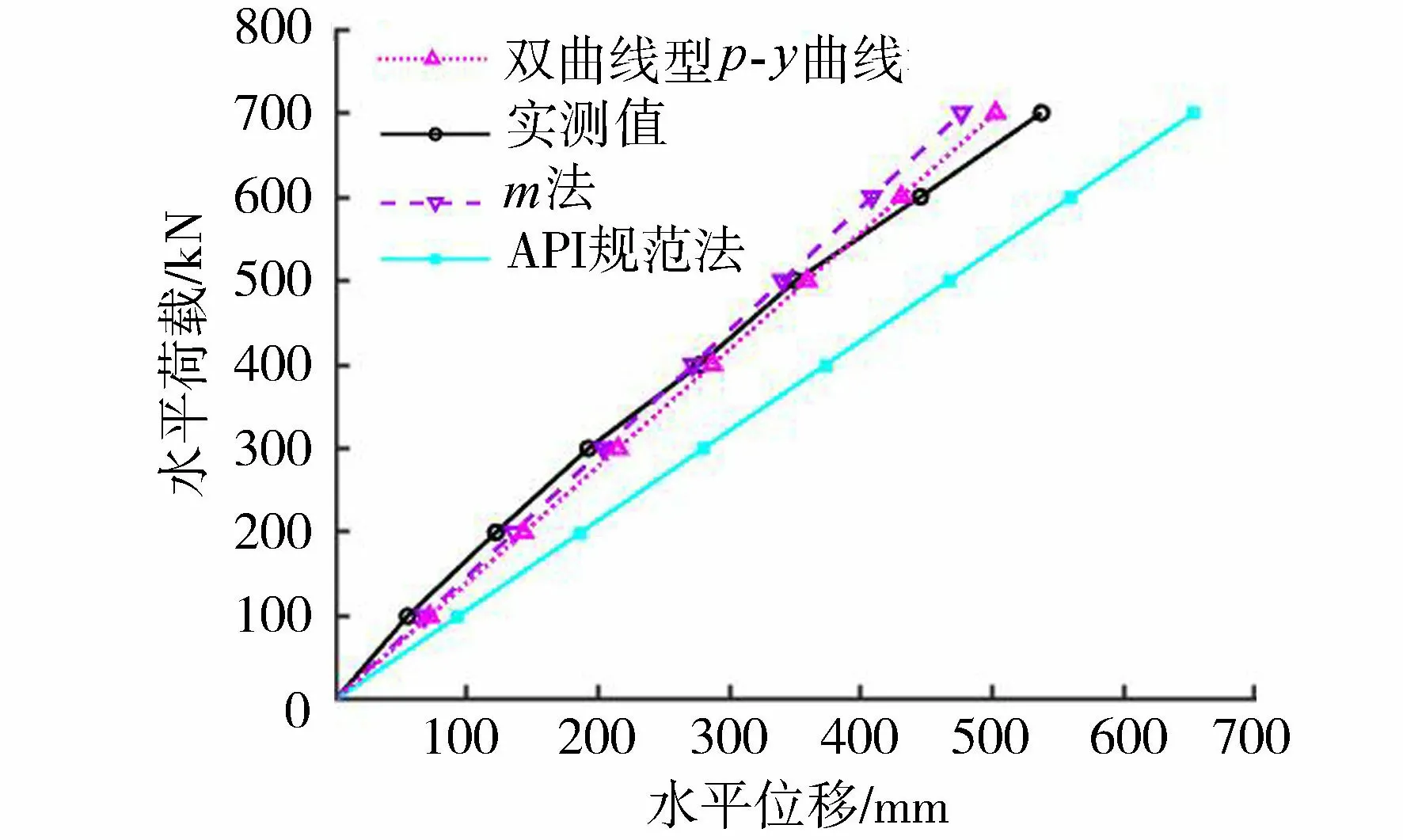
图7 水平静载试桩顶荷载-位移曲线
4 大直径单桩基础水平承载力贡献因素
大直径柔性桩基础与小直径柔性桩桩周土体破坏模式相同,主要为浅层的楔形破坏和深层的平面应变绕桩流动。但是部分学者指出[8,26],现有p-y曲线进行大直径单桩设计时,会高估基础刚度,低估极限承载力,这与本文所得结论一致。对于该现象,Ashour等[27]指出,这主要是由于传统p-y曲线没有考虑侧摩阻力、基底剪力和基底承载力等因素的影响。因此,本文根据不同因素对大直径单桩基础水平承载力贡献的影响建立数值模型进行研究。
4.1 数值模型建立
采用有限元软件Abaqus进行数值模拟,为便于计算,采用1/2对称建模,有限元模型如图8所示。分别建立2m直径、4m直径钢管桩水平受荷模型,壁厚分别为40mm和60mm,埋深为30m,土体深度为50m,宽度方向取30倍桩径。桩单元选用线弹性本构模型,弹性模量取200GPa;土体采用摩尔-库伦模型,选用均质砂土进行单桩基础水平承载力贡献因素分析,土体弹性模量取20MPa,饱和密度取1600kg/m3,摩擦角取38°,膨胀角取8°,泊松比取0.2。桩土间接触采用库伦摩擦形式。由于桩截面对称选取,对该对称面进行垂直向约束,对土体底部和侧面完全约束,桩土顶部自由不受约束。
图8 有限元模型示意图
4.2 水平承载力贡献因素分析
海上风电单桩基础是由正常使用极限状态控制设计的,对单桩基础的水平变形有严格的规定,其泥面处的荷载-位移曲线是单桩基础水平受荷的重要外在表征。以泥面处荷载-位移曲线为表征,定性研究不同因素对大直径单桩基础水平承载力的贡献。
为了便于对比分析大直径单桩的水平承载力情况,对泥面处单桩位移进行了无量纲化处理(即y/D),根据王欢[8]的研究结果,水平极限承载力可以考虑取泥面处单桩水平位移为0.1D时所对应的水平荷载。
分析模型包括正常试验组和对照试验组Ⅰ、Ⅱ和Ⅲ。
a.正常试验组:正常设置的数值模型,未进行特殊处理。
b.对照试验组Ⅰ、Ⅱ:对照试验组Ⅰ和Ⅱ分别将数值模型桩内壁和外壁接触面切向接触设置为无摩擦,以模拟桩内壁、外壁无侧摩阻力的试验工况。
c.对照试验组Ⅲ:通过移除桩内的土塞(桩底以下2m),并设置桩端桩-土相互作用接触面摩擦系数为0,以模拟无基底抗力的试验工况(此时桩内侧摩阻力不存在)。
图9为直径为2m、4m单桩正常试验组和对照组Ⅰ~Ⅲ对应的泥面荷载-位移曲线,可以发现:在桩外侧进行光滑处理后,两根桩的响应刚度均有所下降,此时相同的水平荷载作用下,单桩的泥面位移比正常试验组更大,在泥面水平位移达到极限承载状态(0.1D)时,2m单桩水平极限承载力较正常试验组降低约20%,4m单桩水平极限承载力较正常试验组降低约25%;当桩内光滑处理以及移除桩内土塞时,2m单桩对应的泥面荷载-位移曲线和正常试验组几乎没有差距,4m单桩水平极限承载力有略微下降,约为2%。总体来看,从大直径单桩不同因素的水平承载力贡献可以发现,对于直径较小的单桩基础而言,其侧摩阻力和基底抗力的贡献可以忽略,这也是仅考虑水平土抗力的双曲线型p-y曲线适用的原因。但是随着桩径的增大,侧摩阻力和基底抗力的贡献也随之增大,如果仅考虑水平土抗力,会严重低估单桩的水平承载力。
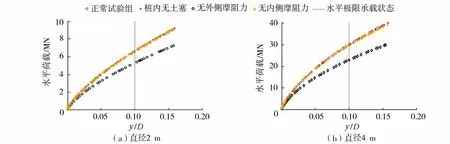
图9 不同直径单桩在不同工况下泥面荷载-位移曲线
5 结 论
a.单桩的桩身挠度和桩身弯矩沿深度方向的分布均表明该试桩水平受荷过程中呈现明显的柔性桩工作特性;试桩力作用点最大实测位移为537.47mm,泥面处位移为79.32m;在泥面以下4倍桩径深度附近出现桩身最大弯矩。
b.对于深厚软黏土地基中的水平受荷大直径桩来说,API规范法与双曲线型p-y曲线在浅层土中p-y曲线初始刚度与桩周土抗力偏大,双曲线型p-y曲线在一定深度下能够较好地预测土反力随位移的变化关系;双曲线型p-y曲线在一定深度下与实测结果较为接近。m法与双曲线型p-y曲线计算的桩顶位移结果在荷载较小时与试验结果较为接近,而随着荷载的逐渐增大,m法与双曲线型p-y曲线的计算得出水平位移较试验值偏小,结果偏向不安全;API规范法计算结果相比试验值较大,计算结果较为保守。
c.随着单桩基础桩径的增大,侧摩阻力和基底抗力的贡献也随之增大,如果仅考虑水平土抗力,会严重低估单桩的水平承载力。对于大直径单桩基础而言,其侧摩阻力和基底抗力的贡献不可忽略,这也是仅考虑水平土抗力的双曲线型p-y曲线不适用的原因,
