基于非密闭气室的风压压损检测与补偿*

沈 坤 张丕状

（中北大学信息探测与处理山西省重点实验室 太原 030051）

1 引言

微气象［1］是研究近地面小范围的气候，是由于某些构造特征（如微地形）所引起的小范围气象要素（温度、湿度、风速风向、气压、雨雪量等）的改变，不至于使大尺度过程（平流、锋面）所决定的天气气候特征发生较大变化，气象部门不能对这些狭小地带的气候情况及时监测和播报，但这些微气象的统计信息在工程建设中具有重要作用。现在很多行业对于微气象测量有越来越强的需求，比如：输电线路［2］、大跨度桥梁［3］、塔吊［4］、风电建设［5］等。因此，需要研究一种可适应外界复杂环境、具备风速测量功能的的新测量技术。

从风压角度分析，流体流动时会产生压强的变化，空气作为流体也具有这种特征，当空气流动时，会产生动压，也称风压，风压的大小与流速呈正相关关系，所以可以通过测量风压的方法来间接测量风速［6］。

目前对于测量特定设备的定向风，通过测量风压方式测量风速，大多数采用皮托管式［7］，只需要考虑来自特定方向的风速，而在自然风测量中，由于风向的不确定性，使用测量风压的方式测风，目前还存在取样方式的问题，采用密闭气室取样要解决产生的谐振问题；而对于非密闭气室要考虑压损的问题。吕永志［8］等针对坦克动力舱排风口气压测量问题，研究了测压取样管道内的空气柱谐振效应对测量的影响。万会雄［9］等在计算超长液压管道沿程压力损失时，建立超长管道数学数学方法：将超长管道针对管道长度求微分得出微小型段压力损失，再对超长管道进行积分便可得到整个管道压损。在实际工程中，除了直管之外，还存在大量弯曲管道。姚利明［10］等根据缩径、扩径圆管压降公式和压力损失规律推导出环空缩径和扩径圆管的压降公式，建立了缩径和扩径圆管数值模型，开展了不同环空变径圆管的流速和压力分布研究，确定了环空缩径和扩径圆管内流体产生不可恢复压降的位置。上述方法针对压损问题通过理论模型计算补偿，可供本文研究借鉴，但是忽略了风压和风速的关系建立，具有一定局限性。

本文针对风动压无法直接测量的问题，采用MEMS 传感器获取风全压，并通过风动压与风全压的关系计算出风动压，再根据风压与风速的数学关系间接实现风速的测量。技术难点其一在于自然风向不确定性，风压取样方式的选取，本文选用非密闭气室进行取样，整个取样结构分为两部分：转动部件与非转动部件，转动部件用来采样，非转动部件实现风速测量，使用非密闭器件来解决转动部件和非转动部件的耦合；其二结构设计方面复杂管件压损计算难题，通过气体管道压损公式推导，建立气体管道压损数学模型，提出一种新的压损补偿方法，成功解决计算压损难点。最终通过风速测试标定实验，对所设计的取样方式进行误差分析，验证了所提方法的可行性。

2 原理

2.1 气体管道压力损失计算

流体力学中，气体管道的沿程压力损失基本式为

式中λ为管道沿程阻力系数，v为气体流速（m/s），d为气体管道的管径（m），l分别为气体管道长度（m），ρ为流体密度（kg/m3）。

局部阻力部件压力损失计算的基本式为

式中n为管道弯头的数量，ξ为局部阻力系数。

根据式（1）和式（2）可计算出气体管道内总的压力损失ΔP为

根据管道压力损失计算公式可知：密闭气室取样，管道内流体速度趋于0 时，压力损失可以忽略不计，进而可知气室内气压等于取样口气压；非密闭气室取样，管道内流体速度不为0 时，需要建立气体管道压损数学模型，提出一种的压损补偿方法，可通过对MEMS传感器测量非密闭气室内风压进行补偿。

2.2 气体管道压损数学模型建立

为了测量不同风向的风压，拟采用风向标技术，通过气室结构、气压取样方式和风速频率特性、稳定性分析等，达到传感器的取样口方向迎风的目的。风压取样结构设计如图1所示。

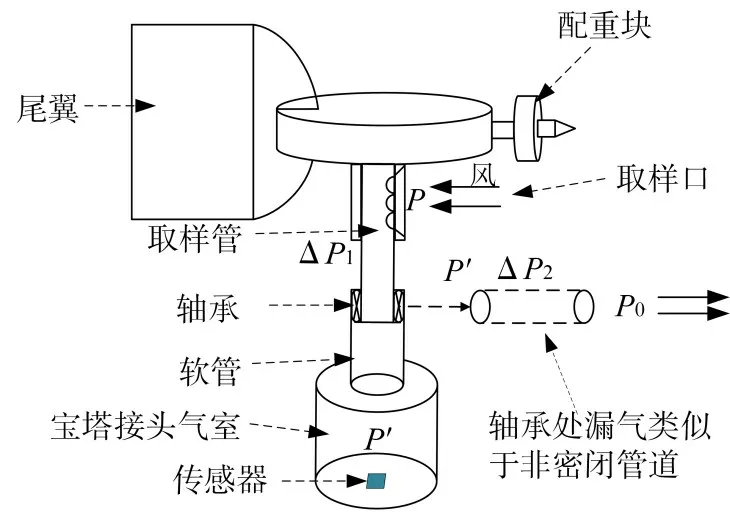
图1 取样模型原理图

根据图1取样结构的设计，整体取样结构为非密闭结构，风从取样口进入取样管，通过软管进入宝塔接头气室，轴承的存在会导致压力损失，压力损失可分为两部分：一部分从取样口到气室内压损称为取样管压损；另一部分从气室到所处环境无风状态下气压称为轴承压损。

取样口气压P与气室内气压P'之间存在如式（4）关系：

气室内气压P' 与同条件下无风状态气压P0之间存在如式（5）关系：

由此可推导出取样口气压P与同条件下无风状态气压P0之间存在如式（6）关系：

其中ΔP1为取样管压损(Pa)，ΔP2为轴承压损(Pa)。

取样管压损与轴承压损既有沿程压损又有局部压损，根据式（1～3）可计算如式（7）、（8）所示：

式中λ1、λ1分别为取样管和轴承摩擦沿程阻力系数，v为管道内气体流速（m/s），d1、d2分别为取样管和轴承气管的管径（m），l1、l2分别为取样管和轴承气管长度（m），ρ为流体密度（kg/m3）。

将式（7）与式（8）进行相比：

整体结构设计完成后，长度l、管道直径d、管道弯头数量n、管道沿程阻力系数λ、局部阻力系数ξ都已确定，式（9）可视为一常数ε；将式（9）带入式（4～6）中，由此推导出：

式中P、P'、P0通过气压传感器测量出来，这样就可以推导出常数ε，就可以得到压损补偿方法，该理论需要实验进一步测量与验证。拟采用方案：使用MEMS 气压传感器测量不同风速下的P、P'，并将数据进行比对分析，验证常数ε的存在。

2.3 风压与风速关系计算

空气从高压流向低压就形成了风，风速的大小与气压梯度基本成正比。根据伯努利方程得出风速与风压关系，风的动压为

其中wp为风压（kN/m2），ρ为空气密度（kg/m3），v为风速（m/s）。

由于空气密度ρ和重度r的关系为r=ρ×g，因此有ρ=r/g。在式（11）中使用这一关系，可得：

在标准状态下（气压为1013 hPa，温度为15℃），空气重度r=0.01225（kN/m3）。重力加速度g=9.8（m/s2），则可以得到：

进而推导出风速计算公式：

由式（14）可知，若测得风压的数据，则可以根据风压来计算风速，通过测量风压间接测量风速。

3 实验方案

随着材料科学、微机械加工技术和微电子技术的快速发展，微机电系统逐步成长起来，它是在微米/纳米技术基础上来完成器件的设计、加工，进而生产出性能优秀、价格便宜、集各类电路和系统为一体的功能系统［11］。气压传感器选用基于MEMS技术的BMP280 芯片，具有高精度、线性和长期稳定性和功耗低，可大批量成产等特点，内部由一个压阻压力传感元件和一个混合信号ASIC 组成，该ASIC 进行A/D 转换，并提供转换结果和具体的传感器通过数字接口补偿数据。BMP280简化方框图如图2所示。

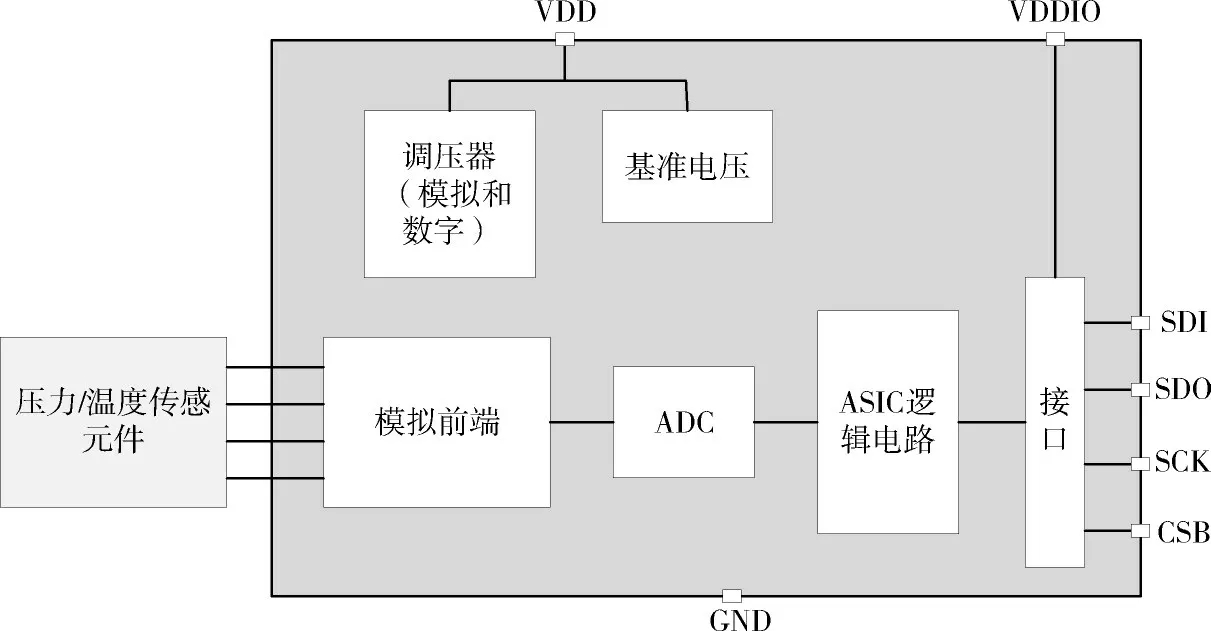
图2 BMP280方框图

由于MEMS传感器测量的绝对精度较低，在低风速下误差大，在目前尚未在风速测量中得到应有应用。但从图3的风速与气压的关系可知，风速越大误差越小，非常适合强风风速的测量，这一特点都使得MEMS 传感器在工程建设规划安全中风速的监测得到应用成为可能。

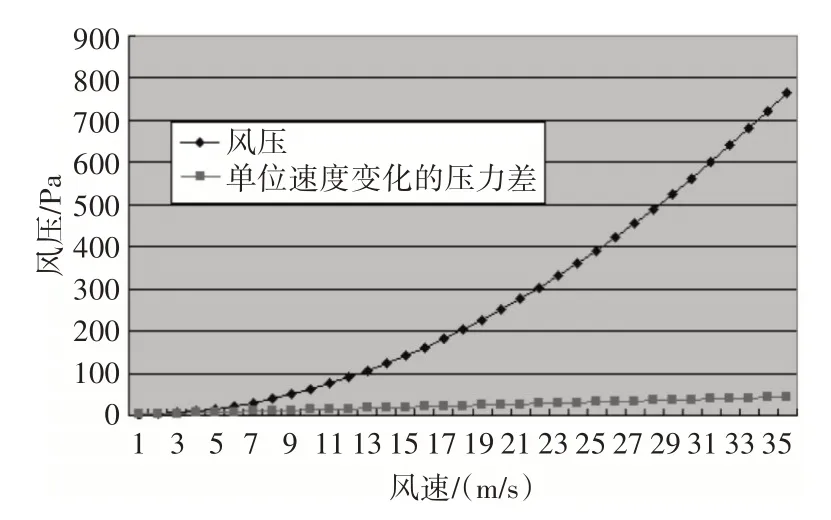
图3 风速风压对照表

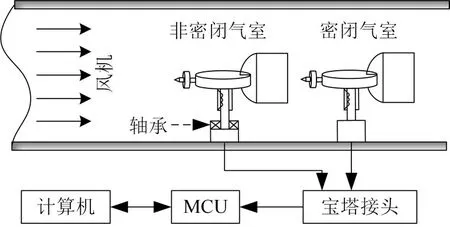
图4 密闭与非密闭气室测试实验

图5 风速测试样机风机标定实验

本文主控芯片选用STM32F103 型低功耗芯片，MCU 作为主设备，BMP280 作为从设备，二者通过I2C 总线进行通信。本项目组在基于MEMS 的电网微气象风速测量方法［12］中使用密闭空间采样，研究表明通过单孔定向风测试验证了3mm×5mm（内径×外径）的硅胶管采样效果最好，长度越短精度越高，并且在风向测试通过发光二极管与三极管外加码盘设计，通过根据三位格雷码设计原理设计而成。本文在此基础上主要对取样口以及取样方式做出了详细设计，取样口由单孔取样改成三孔取样，为了更好地防止野外环境沙尘天气堵塞取样口；取样方式改为非密闭气室，使用非密闭器件耦合方式解决转动部件和非转动部件连接问题。

3.1 非密闭取样压损补偿方法实验方案

本文采用控制变量法，将非密闭气室取样与密闭气室取样同时固定于风机口同一高度位置，为了防止一个位置偶然性，寻找五个测试点进行测试。使用3mm×5mm（内径×外径）的硅胶管分别连接到两个宝塔接头（宝塔接头内放置传感器）。风机产生的风从取样口进入，在气室内形成风压，两块MEMS 气压传感器同时测量。密闭气室测量值为式（10）中P值，非密闭气室测量值为式（10）中P'值，观察两者气压值变化，进而推导出常数ε，及可得到补偿方式。

3.2 非密闭风压取样方式的标定实验

在标定实验中，使用两块MEMS 传感器，一块用于测试当前状态下无风气压值P0，另一块用于测量P'值，加上求取的补偿常数ε，根据式（10）求得当前状态下风的总压。根据动压、静压、全压三者关系，求得风的动压，代入式（14）中，便可求取当前风速。

为了验证取样方式的可行性，本文将取样样机与风杯式测风仪同时放置于风机中，风机变频频率从20Hz～60Hz 以5Hz 为间隔逐步进行多组风速试验，每个频率下样机从0°开始测试，顺时针旋转，以45°为间隔旋转样机，得到传感器测量的风速风向信息，观察两者风速变化，以风杯式风速仪测量的风值为参考对所设计的样机进行相对误差分析。

4 实验结果分析

4.1 非密闭取样压损补偿方法的验证

通过使用两块MEMS 传感器在不同风机频率下同时测量密闭气室气压P、非密闭气室气压P'，经过五个测试点测试记录，将所测真实数据离散点与数据拟合曲线绘制如图6所示。

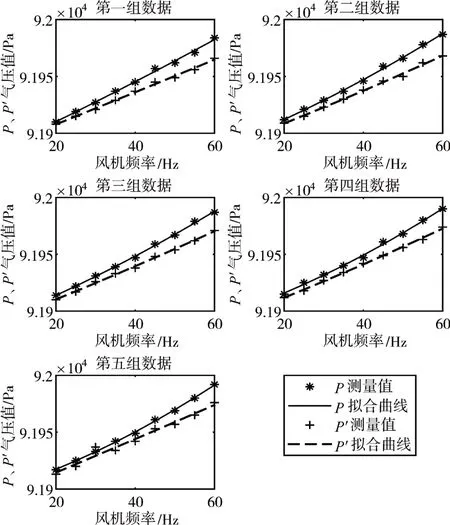
图6 五组数据真实数据离散点与拟合曲线

根据图中测量P与P'的线性拟合曲线可以看出，P、P'之间差值会随着风速的增加而增大。将P、P'同一频率下的数据进行均值计算得到表1数据。通过拟合曲线计算与实际测量，无风状态下气压值P0约为91902.8Pa。

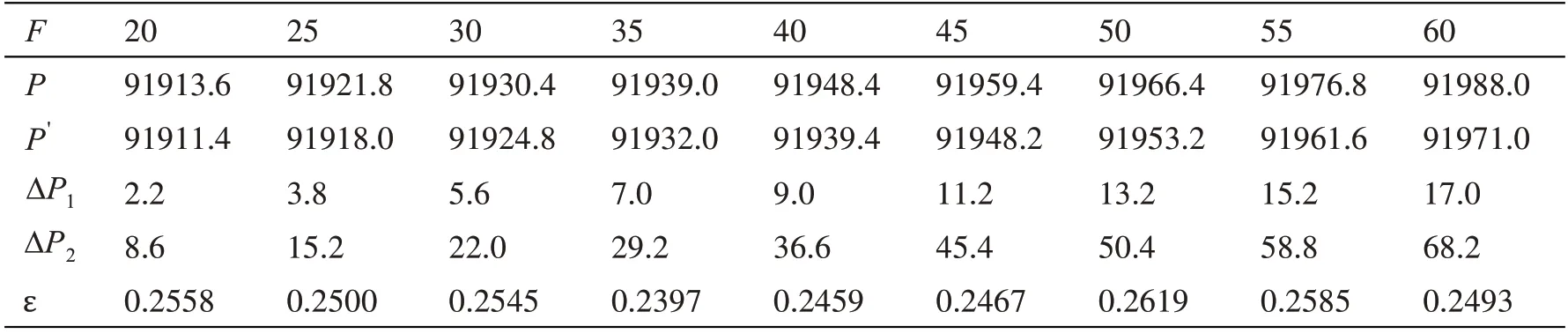
表1 风机不同频率下P、P'、ΔP1、ΔP2、ε 值

根据表1中P、P'数据，再加上无风状态下气压P0值，代入式（10），便可求得常数ε。根据表中数据ε平均值约为0.2514，即得到压损补偿方法。

4.2 风压取样方式标定实验误差分析

通过标定实验，传感器样机总共得到九组实验，并与参考风速进行对比，计算相对误差比。图7所示为八个方向不同风速段相对误差比。

图7 风速测量相对误差

图中坐标图上方风速值为风杯式测风仪在不同风机频率下的风速值。由图7实验数据表明：整体相对误差比不超过5%，通过9 组相对误差比曲线图对比风速越大相对误差越小，风速达到11m/s时相对误差不超过2%。通过此对比试验，便可证明此设计方案的可行性。

5 结语

本文提出一种基于非密闭气室的风速测量方法，突破了风向自适应的风压取样方法以及复杂构件的非密闭气室的风压计算难点，解决了非密闭气室内风压损失的问题。根据气体管道压损公式建立数学模型，提出一种新型的压损补偿方法，最后根据风压与风速关系间接计算风速。本文针对风压取样方式结构进行特殊处理，使用非密闭器件耦合转动部件与非转动部件，将设计的取样结构在风机中进行试验。通过风压取样方式标定实验并对实验数据进行误差分析，验证了本文所提方法的可行性。

本文通过数据求得的补偿常数ε试验风速范围仅在0～12m/s，至于大于12m/s 风速下是否还会存在并且相对误差的大小还需要进一步验证。