基于超宽带非对称双边双程测距的矿山井下定位跟踪算法研究
2023-06-05林正鸿黄麟淇李涵王碧博王志翔陈心怡
林正鸿 黄麟淇 李涵 王碧博 王志翔 陈心怡
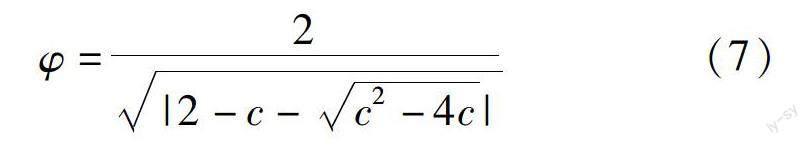
摘要:在地下矿山建立稳定、有效、高精度的人员定位系统和算法,对矿井事故灾害的灾时指导逃生和灾后救援等方面起着至关重要的作用。基于超宽带定位测距系统,进行了室内非对称双边双程测距试验,利用粒子群算法、Taylor级数迭代等智能算法完成对目标的定位,以期获得更精确的定位解析,相较于传统的Wi-Fi通信系统及射频识别人员定位管理方法,能够在保证实时性的同时,有效、准确地提供遇险人员的位置及周边地形状况,达到了厘米级定位精度,实现了井下精确定位,为井下救援工作提供技术支持。
关键词:井下人员定位;跟踪算法;非对称双边双向测距;超宽带;粒子群算法;Taylor
迭代算法
中图分类号:TD65文献标志码:A开放科学(资源服务)标识码(OSID):
文章编号:1001-1277(2023)04-0028-06doi:10.11792/hj20230408
引 言
矿山井下人员定位管理一直是矿山安全监管的重要内容,根据《中华人民共和国安全生产法》有关规定,矿井安全避险系统作为矿山生产建设中不可缺少的部分,有关矿山企业必须建立完善的安全配套设施,做到对入井人员数量、状态、位置及行动路线的实时监测,充分保障入井人员生命安全。基于上述要求,井下人员定位系统需完成位置信息收集、输送、分析等综合功能,同时对于位置信息,应能够及时反馈高精度的相关数据和对人员行动路线的预测等动态信息,并能够实时拟合紧急救援方案,为救援工作提供人员定位数据和救援参考方案。
目前,主要的矿山无线通信和人员定位管理系统包括射频识别(Radio Frequency Identification,RFID)人员定位管理系统[1]、Wi-Fi通信系统等。通过搭建以太环网并作为主传输平台,利用IP网络通信技术、Wi-Fi无线通信技术[2]、RFID射频定位技术[1],在矿井中实现多功能应用。RFID人员定位管理系统和Wi-Fi通信系统均以无线AP和ZigBee通信协议的RFID射频定位技术为基础[3-4],达到无线移动通信和精准人员定位的要求,通信和定位主要靠综合基站实现,但在发生灾害时无法保证设备有效性。而超宽带(UWB)[5]测距系统可获得更为精确的定位数据,且可在近期获得的历史人员定位数据基础上,结合位于地面的智能算法进行拟合定位,最大限度地降低设备因素对精确性的影响,实现在灾害发生后,设备受损的情况下快速准确地定位出受困人员位置,便于施救。
现今人工智能算法技术愈加成熟且应用领域广泛,而将人工智能算法技术与目前使用的定位系统相结合,实现对矿井下目标的精确定位[6-9]将是未来的发展趋势。
1 超宽带原理
1.1 UWB无载波定位技术
常用于井下人员定位[10-11]的技术包括红外定位技术、蓝牙定位技术、Wi-Fi定位技术、超声波定位技术、ZigBee定位技术等,但是大多数定位技术存在传输距离短、定位精度低、抗多径效应差等问题,使得在井下复杂地质条件下难以实现对人员的精确定位[4,12-13]。
作为一种无载波通信技术,UWB无载波定位技术[14-15]与传统通信技术存在许多差异。一方面,UWB不发射载波传递信号,而是发射ns至ps级的非正弦波窄脉冲来实现传输数据的目的。因此,它占据了3.1~10.6 GHz间7.5 GHz带宽频率的频谱范围;另一方面,UWB适用于高速、近距离无线个人通信ns级窄脉冲传输无线信号。相比于其他无线定位技术,UWB无载波定位技术具有节能环保、精度高、信号范围大、成本较低等优势,能较好满足工业级定位要求。
1.2 UWB无载波定位技术原理
UWB无载波定位技术原理是在拟搜索区域内设置若干UWB定位基站,并与待定位对象所配置的UWB定位标签进行信号交流,发射测距请求,从而测量出定位标签与定位基站的距离(或伪距)关系,利用所测数据,结合数学分析方法求解定位标签的具体位置。
目前,应用效果较好的定位方法[16-18]主要有:到达时间(Time of Arrival,TOA)法、飞行时间测距(Time of Flight,TOF)法和到达时间差(Time Difference of Arrival,TDOA)法3种。基于TOA的定位方法,通过使用测距方法获得定位传感器和目标节点之间的线性距离,并且每次TOA测距估计结果对应一个圆方程。而基于TDOA的定位方法也是基于线性距离测量,与TOA法不同的是,基于此方法得到的数据结果是定位传感器与目标节点之间的距离差,并且針对每个时间差距离估测结果在数学上设立一个与之对应的双曲线方程。当然,无论是通过圆方程还是双曲线方程,定位测距的最终目的都是将距离代入对应的数学方程联立求解目标节点的位置,联立形成的方程越多,所得出的节点坐标就越精确,这也是基站数量越多,位置越精确的原因。但二者均存在定位精度有限、严格时钟同步、时钟偏差等问题。
TOF是一项基于双向测距原理的新型测距技术,它以规避时钟偏差,降低定位误差为目标,该方法以UWB信号在定位基站与拟定位目标之间的往返飞行时间为基准,并结合公式定理计算相对距离。根据几何关系可以得出,平面内某点到已知点的距离为常数时,该未知点一定落在以已知点坐标为圆心,以该常数为半径的圆上。有2个已知点,就有2个交点。以3个已知点和距离作3个圆,他们交于同一点,该点就是标签的位置。因此本次研究采用TOF测距技术。
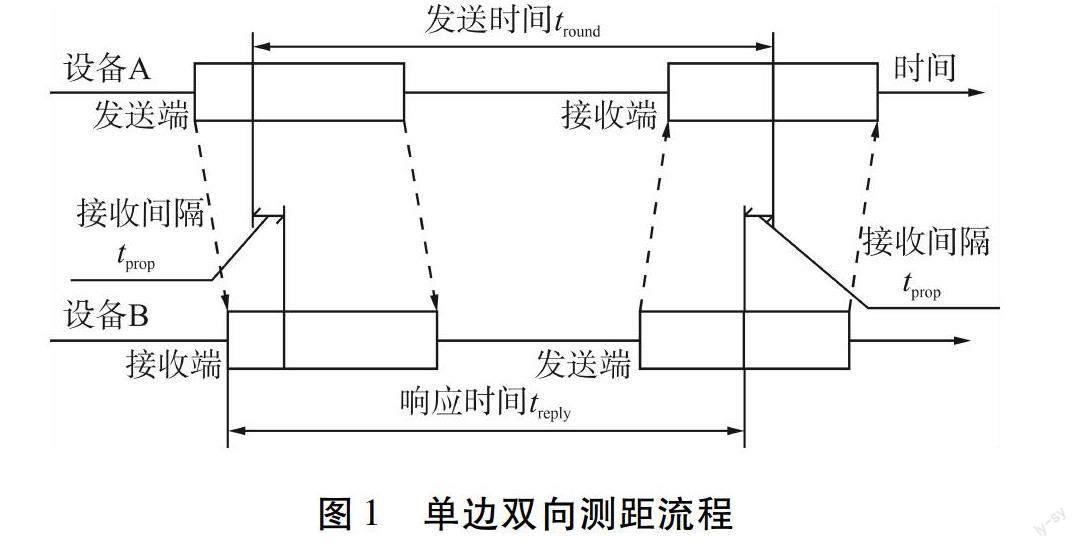
TOF测距技术又分为单边双向测距和双边双向测距两种方法。
1)单边双向测距(Single-sided Two-way Ranging,SS-TWR)是对单个往返消息时间上的简单测量(如图1所示),设备A主动发送数据到设备B,设备B返回数据响应设备A[17]。
2)双边双向测距(Double-sided Two-way Ranging,DS-TWR)是在单边双向测距方法基础上进行扩展的一种测距方法(如图2所示),其相较于单边双向测距增加了记录两个往返的时间差,进而得到飞行时间,此方法显著降低了测距方法带来的系统误差。
在双向测距中,测量精度主要受设备时钟漂移系数之差、设备B的响应延时等因素影响,本系统采用更高精度的非对称双边双向测距(Asymmetric Double-sided Two-way Ranging,ADS-TWR)[19]技术,在理论范围内,尽可能减少不良因素对测量精度的影响,以达到提高定位精度和定位实时性,减少数据传输时间的效果。
1.3 ADS-TWR测距技术
通过对标签基站进行双向测距,并利用基站与标签之间UWB信号的单向平均传播时间(ttof)[17]进行ADS-TWR测距,测距原理如图3所示。
移动标签将响应时间(treply)、发送时间(tround)值通过终止帧(Final)发送到基站,基站利用treplyA、treplyB、treplyC的值,进行相应的数据处理,计算标签与基站之间的UWB信号单向平均传播时间(ttof),其由式(1)计算得出。
已知电磁波的传播速度为3×108 m/s,代入速度时间公式后,可得到准确的基站与标签之间的距离(d)。
2 井下人员定位算法
2.1 定位算法的改进
各测量基站运用测距技术对定位标签测量后,相关距离数据由UWB无载波定位技术传输至总基站,并运用定位算法对数据进行处理以实现对目标的精确定位,找到目标在空间系统的坐标值。目前,现行使用的算法中,以Taylor迭代算法[20-23]为当下较优算法,但其不足之处在于其受算法初始值准确性的限制,定位精度不足。为较好规避Taylor迭代算法自身的结构性弱点,本文将结合标准粒子群(PSO)[24-25]算法,初步求解数据的定位方程组,提高Taylor迭代算法初始值的精确度后,再进一步利用Taylor迭代算法求解标签距离数据所指向的具体坐标。将PSO算法及Taylor迭代算法二者有机结合后,能够实现提高定位精度的要求。
2.2 PSO算法
PSO算法是一种动态群体优化智能算法。对于求解定位标签的实际具体位置,本文将以测距数据为基础求解目标定位问题转化为求解以测距数据为基础的非线性方程组最优解的动态规划问题。对于此方程组的求解,PSO算法体现出考虑参数范围小、粒子收敛速度快(即得出最优解速度快)、方便快捷的特点。
设在有限维度的搜索空间条件下,非线性方程组的n个解可用数量为n的粒子群代替,通过不断修正粒子速度与粒子位置这两个参数,来驱使粒子不断搜索所设空间中的最优位置,即非线性方程组的最优解,粒子群速度(vi)公式见式(2)、式(3)。
粒子的位置:
式中:k为粒子群当前迭代次数;pbi为第i个粒子当前的个体最优值;gbi为种群当前的全局最优位置;c1、c2为非负学习因子;r1、r2为[0,1]的随机数,用于保证个体差异性;w为惯性权重,主要修正算法的局部与全局搜索能力。
粒子的个体速度按上述公式进行变化,且已知粒子速度主要由惯性权重[26]、学习因子[27]决定。针对这两种参数如何选择和变化,可以从惯性权重变化函数和学习因子动态变化函数两个方面进行考虑。
2.2.1 惯性权重变化函数改进
由式(2)可知,惯性权重主要影响粒子的速度,而速度大小将影响粒子的搜索范围大小。因此,惯性权重的取值对于粒子群算法的收敛程度及寻优结果影响较大。通过建立wmax、wmin的函数关系对惯性权重进行调整,现行常调用线性递减函数[28-29]来调整惯性权重,该函数在算法开始时保持较大的惯性权重,以充分保证粒子在初期搜索更多区域,体现较强的全局搜索能力,随着数据迭代次数的不断增加,惯性权重值相应递减,搜索区域进一步收敛,粒子在最有可能出现最优解的局部区域进行更为细致的搜索,同时不斷加快收敛速度。
惯性权重按照式(4)进行变化。
式中:T为终止迭代次数;wmax、wmin为惯性权重的最大值和最小值,分别取0.9和0.4。
针对粒子群算法的拟合结果,需要构建一个评判标准来对算法拟合结果的精确程度进行评价。设f(xi,yi)为定位标签与n个定位分站的测距总和,那么构建的适应度函数为:
式中:ri为测量半径(m)。
在粒子全局搜索最优解的过程中,若根据函数评价得出本次结果的适应度值比前一次更高,将会对当前粒子群速度公式中的pbi、gbi进行更新,否则粒子将进入下一轮搜索并根据适应度函数再次进行调整。
目前,使用的线性递减函数能够较有效地调整惯性权重,以期达到利用精确的粒子群求解最優解的效果,但线性递减函数仍存在初值搜索范围相对固定,迭代变化为静态,且惯性权重取值存在系统误差,无法根据适应度变化而调整的弊端。针对此函数所暴露的缺点,本项目创新性地提出以适应度为参考因素的自适应调整权重函数,见式(6)。
式中:f为当前适应度值;fmin为最小适应度值;favg为平均适应度值。
引入适应度值作为参考因素,能够使惯性权重根据适应度值变化进行自我调整,并不断选取适应度更高的惯性权重值以对粒子速度和收敛趋势加以约束。采用本函数实现惯性权重值的控制,其优点在于能够在粒子搜索初期保证足够的搜索范围,相比于线性递减函数能更快地使粒子群趋近于全局最优解,实现了计算的动态控制和计算量的减少,在算法结构上更加简洁。
2.2.2 学习因子c1、c2动态变化函数
使用较为广泛的粒子群算法中,粒子群速度公式中非负学习因子c1、c2[30-31]取值一般默认为常数2。但当学习因子为定值时会导致粒子在寻找最优解时缺乏更为精确的目标,从而造成前期、后期粒子移动目标差异性不足,算法效率严重降低。针对该问题,提出两种有待实验验证的方案:
1)方案一:异步变化学习因子。在不断寻找局部最优解的过程中,不同的学习因子随时间呈现出不同规律的变化称为异步变化。如果c1的取值过大,将使得粒子在局部范围内过多徘徊,进而使得搜索效率降低、算法速度减慢、浪费计算量。而较大的c2值,则又会促使粒子过早收敛到局部最小值,从而严重降低寻找更大范围内最优解的可能性。
2)方案二:引入压缩因子。为达到人为控制粒子飞行速度的目的,使粒子速度更好地在全局搜索和局部搜索之间达到有效平衡,更快更好地找到全局最优解,可引入压缩因子(φ)进行算法优化,其优化原理见式(7)。
式中:c=c1+c2,c>4,一般取4.1(预设参数中可令c1=c2=2.05)
c1、c2常用取法有:
(1)c1=c2=2.05,压缩因子φ=0.729,在形式上可以等效w=0.729,c1=c2=1.494 45的基本PSO算法。
(2)微粒规模N=30,c1=2.8,c2=1.3,压缩因子φ=0.729。
通过上述参数的调整,实现对粒子群速度的有效调整。
3 试验结果与定位算法分析
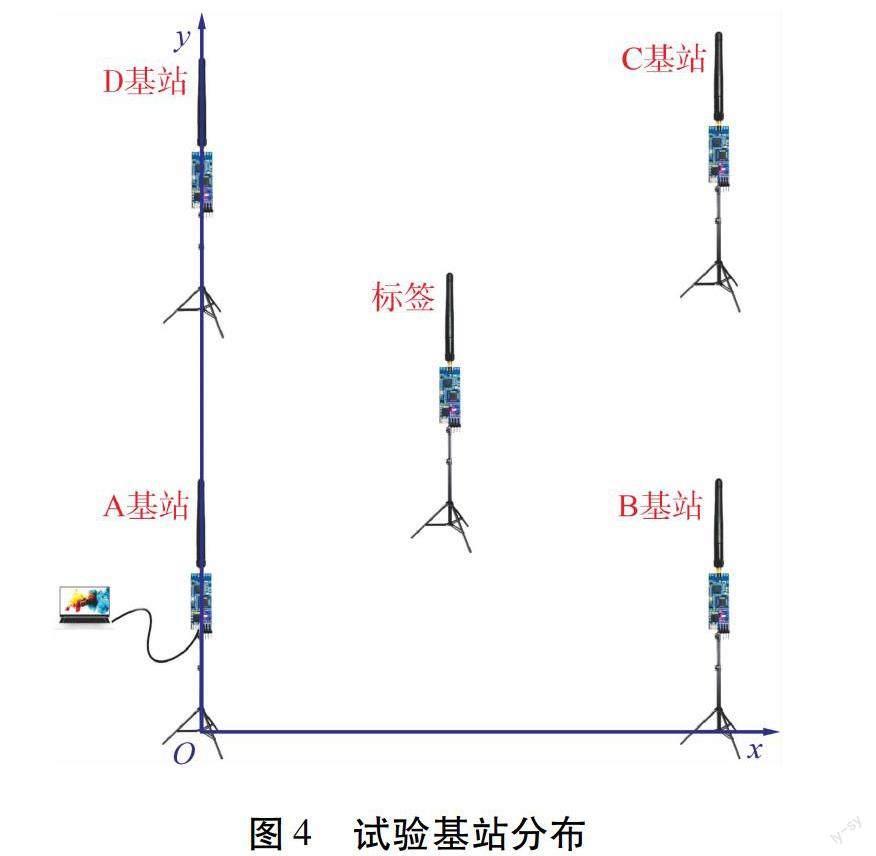
假设有4个基站,如图4所示,其位置分别是A(0,0),B(50,0),C(50,50),D(0,50),每个基站的通信半径为60 m。
移动标签信号实时确定标签信号距离各个基站的距离,当标签信号位置为1,2,3,4,5,6时,部分距离信息如表1所示。
将距离信息代入改进后的PSO算法中,经过MATLAB仿真的标签信号预计初始位置坐标如表2所示。
将得到的标签信号初始坐标代入Taylor迭代计算中完成对标签信号的定位。在相同仿真情况下,使用标准的TDOA定位方法对初始标签信号定位,综合两种定位方法得到标签信号的坐标如表3所示。
对比实际坐标,优化定位坐标及标准TDOA定位坐标可得到其散点图,如图5所示(横纵坐标均表示为坐标值,连线以示区分)。
4 结 论
本文基于超宽带(UWB)非对称双边双向测距(ADS-TWR)技术,利用距离各个基站所测的精确位置信息,将粒子群算法、Taylor迭代算法有机结合,完成对目标位置的定位与解析,得出以下几点结论:
1)通过采用PSO算法获取精确初始值,再运用Taylor算法迭代分析的运算模式,能使所得坐标与真实坐标显著接近,同时相较于目前的标准TDOA定位方法有较为明显的精度提升。
2)目前优化后的运算模式已经能够将大部分坐标的精确度提升至厘米级别,但部分坐标的误差仍然较大,有待进一步优化。
3)未来的工作将讨论在现有的运算模式基础上,如何结合实际案例和现场分析,利用实验室建模操作来进一步调整粒子群算法中的学习因子初始值及压缩因子取值,从而调试出最合适的算法参数,为井下救援提供更有效、精准度和鲁棒性更强的优化参数算法。
[参 考 文 献]
[1] 邵国强.矿用无线通信及人员定位管理系统设计[J].工矿自动化,2013,39(3):10-12.
[2] 张鹤丹,卢才武.基于WiFi技术的井下人员定位系统研究[J].金属矿山,2012(9):99-102.
[3] 蒋磊,于雷,王振翀,等.基于WiFi和ZigBee的井下人员无线跟踪与定位系统设计[J].工矿自动化,2011,37(7):1-6.
[4] 张定国.基于ZigBee技术的煤矿井下人员精确定位研究[D].太原:太原科技大学,2016.
[5] 刘书伦,王树森.基于超宽带技术的井下人员定位系统[J].工矿自动化,2014,40(10):81-83.
[6] 毕林,王黎明,段长铭.矿井环境高精定位技术研究现状与发展[J].黄金科学技术,2021,29(1):3-13.
[7] 方文浩.基于UWB的煤矿井下高精度定位技术研究[D].合肥:合肥工业大学,2018.
[8] 张岩松.基于UWB技术的煤矿井下人员精确定位系统研究[D].徐州:中國矿业大学,2021.
[9] 王洋洋,郭长娜.煤矿井下人员精确定位方法[J].中国新通信,2020,22(11):83.
[10] 邓凯伦.井下人员定位系统的研究[D].西安:西安工程大学,2015.
[11] 叶伟.煤矿井下目标定位的研究现状与展望[J].中国矿业,2021,30(1):82-89,105.
[12] 李夕兵,王世鸣,翁磊,等.Damage constitutive model of different age concretes under impact load[J].Journal of Central South University,2015,22(2):693-700.
[13] 张楚旋,李夕兵,董陇军,等.顶板冒落前后微震活动性参数分析及预警[J].岩石力学与工程学报,2016,35(增刊1):3 214-3 221.
[14] AL-GBURI A,IBRAHIM I,ZAKARIA Z,et al.High gain of UWB planar antenna utilising FSS reflector for UWB applications[J].Computers,Materials & Continua,2022,70(1):1 419-1 436.
[15] SUBUH P,FERI A,SRI S.Improvement of the performance characteristic of UWB antenna using a novel double-layer FSS operating at the Ku-Band[J].Wireless Personal Communications,2021,121(4):3 297-3 308.
[16] 周仁斌.基于UWB技术的煤矿井下人员精确位置监测系统设计[J].煤矿机械,2022,43(6):181-184.
[17] 姜文峰.基于区域判定的超宽带井下高精度定位[J].电子世界,2019,561(3):193-194.
[18] 郭爱军.UWB技术在煤矿井下的应用[J].陕西煤炭,2021,40(3):51-54.
[19] 刘永立,吴闻轩,单麒源,等.井下人员定位的超宽带TWR改进算法[J].黑龙江科技大学学报,2021,31(2):135-139.
[20] 康婷,魏胜非.基于混沌粒子群与Taylor算法的协同定位算法研究[J].仪表技术与传感器,2019(1):118-121.
[21] 谢芝玉,刘雄飞,胡志坤.基于Taylor展开的UWB井下定位算法研究与实现[J].计算机工程与应用,2017,53(2):231-235.
[22] 刘倩,夏斌,谢楠,等.基于多元Taylor级数和AFS的混合定位算法[J].计算机仿真,2020,37(4):290-293,370.
[23] 江晨芳,侯克鹏,孙华芬.基于GM(1,1)模型的矿业安全生产事故预测分析[J].黄金,2013,34(12):63-67.
[24] 冯茜,李擎,全威,等.多目标粒子群优化算法研究综述[J].工程科学学报,2021,43(6):745-753.
[25] 钟倩漪,钱谦,伏云发,等.粒子群优化算法在关联规则挖掘中的研究综述[J].计算机科学与探索,2021,15(5):777-793.
[26] ZHAO Q,LI C W,ZHU D,et al.Coverage optimization of wireless sensor networks using combinations of PSO and chaos optimization[J/OL].(2022-03-09)[2022-10-2].https:∥doi.org/10.3390/electronics11060853.
[27] DUTTA M K,KAUR M,SARKAR R K.Comparative performance analysis of fuzzy logic and particle swarm optimization (PSO) techniques for image quality improvement:With special emphasis to old and distorted folk paintings[J].Optik,2022,254.
[28] 罗平,向凤红,毛剑琳,等.基于自然选择的线性递减权重PSO与Taylor算法的TDOA协同定位算法研究[J].计算机应用研究,2014,31(4):1 144-1 146,1 150.
[29] 刘永立,吴闻轩.井下超宽带人员定位的改进卡尔曼滤波算法[J].黑龙江科技大学学报,2021,31(4):500-505.
[30] 孙彦景,霍羽,陈岩,等.矿山动态协同作业场景无线通信关键技术[J].煤炭学报,2021,46(1):321-332.
[31] 毕林,段长铭,任助理.基于RANSAC的地下矿山巷道边线检测算法[J].黄金科学技术,2020,28(1):105-111.
Study of underground locating and tracking algorithm in mines based on ultra-band asymmetric bilateral two-way ranging
Lin Zhenghong,Huang Linqi,Li Han,Wang Bibo,Wang Zhixiang,Chen Xinyi
(School of Resources and Safety Engineering,Central South University)
Abstract:It plays a vital role in runaway guidance and post-disaster rescue in mine shaft accidents to establish a stable,effective,and high-precision personnel locating system and algorithm.Based on the ultra-band locating ranging system,the study carries out tests on indoor asymmetric bilateral two-way ranging.In the test,particle swarm optimization,Taylor series iteration,and similar smart algorithms are used to complete the target location,in hope that a more precise location analysis is obtained.Compared to conventional Wi-Fi communication systems and frequency-emission personnel location identification methods,the method,as well as guaranteeing real-time information,can effectively and accurately provide the location of troubled personnel and their peripheral terrain status.Besides,the precision of locating reaches the level within centimeters,which realizes precise underground location and provides technical support for underground rescue.
Keywords:underground personnel location;tracking algorithm;asymmetric bilateral two-way ranging;ultra-band;particle swarm optimization;Taylor series iteration algorithm
