“探索筝形”数学活动课堂教学实录与思考

高铭

【摘要】为了让学生能够综合运用数学知识解决实际问题，提高实践能力，教师可以将数学活动课应用到教学实践中.数学活动课通常是以学生为主体，围绕具体问题开展活动，以此培养学生分析问题和解决问题的能力.文章以“探索筝形”这节数学活动课为例，让学生通过自主探索的方法，主动利用从特殊到一般的数学思想，了解图形的性质和特点，掌握研究数学的基本方法，为以后学生将数学知识应用于实际生活打下坚实基础.

【关键词】筝形；全等；类比；数学活动

引 言

数学教育要面向社会现实，课堂教学就必须要联系生活实际，注重培养和发展学生发现数学问题的能力.本节课是在苏教版八下数学第9章“中心对称图形———平行四边形”“矩形、菱形、正方形”学完之后，补充的一节数学活动课.学生通过本节课的教学活动，能够了解筝形与菱形、正方形之间的区别与联系，掌握从特殊到一般的数学思想，最终将所学应用到实际生活中.

以下为课堂实录：

一、引入———初识筝形

课前准备：平时学生跳绳用的绳子.

活动一：上课伊始，教师让一名学生来做一个动作（如图1）：手捏着绳子的两个最顶端，双脚并拢，人站立在绳子上，脚踩在绳子的最低处，挺直腰杆、伸直手臂并拉紧绳子.

师：（请大家来观察）如果将这名同学的头、两只手、并拢的双脚都近似地看作数学中最基本的圖形———点，那么从整体看，这是一个什么图形？它有什么特点？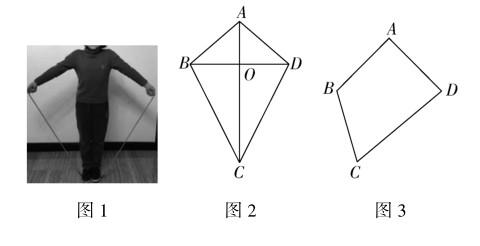

生1：这是一个四边形.

生2：感觉这是一个轴对称图形.

生3：这个图形可以看成由两个全等三角形组成的.

生4：它有两组边分别相等.

师：大家说得都很好！

学生回答问题的同时，教师在黑板上画出图形（如图2），并结合学生的回答进一步给出定义：在四边形ABCD中，AB=AD，CB=CD.像这样的，有两组邻边相等的四边形叫筝形.

师：请同学们看一看，老师画的这个图形（图3）是筝形吗？在这个图形中，它也符合“有两组邻边相等”这个条件，但是它为什么不像筝形呢？

定义中为什么一定要写“像这样的”.“这样”是怎样的呢？是“两组邻边”的位置要在对角线BD的两侧，否则两组邻边相等的方式还有图3中的AB=AD，AB=BC.而图3中的图形并不是我们要研究的筝形.我们给出的定义一定要体现数学的严密性.

【设计思路】会观察是研究数学第一步，是数学活动中最基本的元素.眼睛观察到的东西能够快速地让学生有直观的感受.活动一中，用我们生活中常见的绳子作为道具，再配合相应的动作，能够让学生轻松说出自己熟悉的风筝形状，并且能够非常直观地得出“有两组邻边相等”这个条件，为后面进一步探索做铺垫.

二、探索活动———探究筝形

（一）风筝的由来

师：大家知道风筝是怎么来的吗？从什么时候开始有风筝的呢？“筝”字为什么是竹字头呢？

最早的风筝是用木头做成的，那个时候叫“木鸢”，比较重.后来鲁班选用了更轻的竹子为材料并加以改造.最早，风筝只是用来传递信息的，后来才在民间流行成一种玩具，并有了一个好听的名字“纸鸢”.到了晚唐时期，渐渐演变成风筝.

师：风筝到底有什么特点，能够在古代就成为重要的军事用具呢？请同学们一起来研究一下.

【设计思路】要让学生更好地研究筝形，就要让学生对它产生兴趣———风筝的由来.往往知识背后的东西都源于真实的情境.本活动的创设成功激发了学生对风筝的好奇心，进而让学生从不同的方面来细细研究筝形的性质.

（二）活动二：探索筝形的性质

课前准备：教师提前将学生分成4组.

师：请大家来回忆一下，之前我们学习四边形的时候，是从哪几个方面来研究图形的？

生：我们是从图形的对称性、边、角、对角线这几个方面来研究的.

师：那么就请每一组同学选择一方面进行研究，然后上台将你们组的研究结果展示给大家.

小组1：我们组研究的是图形的“对称性”.我们发现筝形是一个轴对称图形，对称轴是对角线AC所在直线（如图2）.

师：怎么用数学方法来证明筝形是轴对称图形？

小组1：根据筝形的定义，可以证明△ABC和△ADC全等，就能证得筝形是轴对称图形.

小组2：我们组研究的是“边”.筝形中有两组邻边相等，AB=AD，CB=CD.这一点在筝形的定义中就已经写明了.

师：请思考下如果在满足这个条件的前提下，我们适当地改变两组邻边的长度，你们还有什么发现？（提问的同时在白板上演示动画，让学生有初步的感知.

小组2：当筝形中四边都相等时，它就变成了菱形！

由此，学生有了进一步的探索结果———菱形是特殊的筝形.

小组3：我们组研究的是“角”.在图2中，我们发现筝形中有一组对角相等，还有4对相等的锐角.由等腰三角形中的“等边对等角”和三角形全等可以证得.

小组4：我们组研究的是“对角线”.筝形的对角线互相垂直，AC垂直平分BD.

师：非常好！那么如果调整AC和BD的长度和位置，当AC与BD互相平分且相等时，大家又有什么发现？（调整白板中的图形）

生齐答：这个时候的筝形就变成了正方形！

师：大家说得非常好！那么我们所熟悉的菱形和正方形与今天刚认识的筝形到底有什么区别和联系呢？我们同样从上述研究的四个方面来比较一下（给出表格）.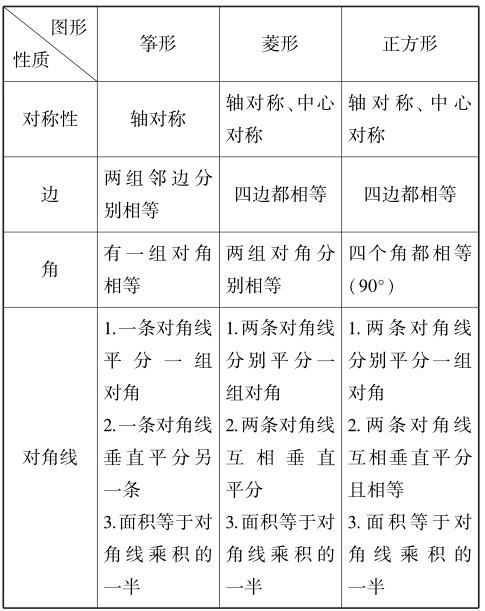

【设计思路】分组研究，不但能让人人参与，还能在课堂有限的时间内完成学习任务.研究结果分享交流也是数学活动课的重要环节之一，可以加强学生的主体性.构建主义认为学生学习是学生自己构建知识的过程，是根据自己已有的认知，对外部信息进行主动选择、加工和处理，从而获得知识的过程.本活动中，教师先让学生回忆是如何研究平行四邊形的，再引导学生通过类比的数学方法自主探索出筝形的各种性质.教师适当地指导和提问，可以引导学生更全面地去探索问题，并让他们感受到从特殊到一般的数学思想，进而在研究的过程理解数学原理、触及数学本质.

（三）活动三———作出筝形

课前准备：学生自备圆规和直尺.

师：现在同学们已经了解了筝形的性质，那么你能利用手边的圆规和直尺作出一个筝形吗？

学生给出了作法，并说明了作图原理.

作法1：画任意一条线段AB，再作AB的垂直平分线，在这条垂直平分线上、线段AB两侧分别找点P，Q，连接AP，BP，AQ，BQ即可（如图6）.

生1：我们知道筝形中有两组邻边相等，所以我就想到了垂直平分线的性质：垂直平分线上的点到线段两端点距离相等.这样就有和定义一样的两组邻边相等了.

作法2：画线段AB，在线段外有一点C，作点C关于线段AB的对称点D，再连接AC，AD，BC，BD（如图7），可构成筝形.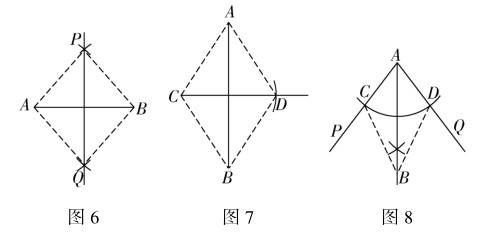

生2：我这样画是因为筝形是轴对称图形，先固定好对称轴，接下来我只需要作对称点，再连接四个点即可.

作法3：任意画一个角∠PAQ，在角的两边截取相等的线段AC，AD，再作出这个角的角平分线，在这条角平分线上任意找一点B（不与点A重合），连接BC，BD即可（如图8）.

生3：我想到的是筝形中它的对角线平分一组对角，再结合对称性得到的.

师：同学们的作法都非常棒！大家从筝形的轴对称性、边、角、对角线这些不同的方面作为切入点，都作出了漂亮的筝形！

【设计思路】动手操作也是研究数学的重要手段.在本节数学活动课中，同学们不但有自己动手操作的机会，也有向别人学习的机会.最后通过学生自己作图，进一步加深了对筝形的理解，学生的基本素养也得到提高.

三、数学应用———再探筝形

例 如图9，在矩形ABCD中，E，F分别在AB，BC上，EF∥AC，将△BEF沿着EF翻折，点B的对应点为点G.

如图10，若∠BFE=30°，当点G落在AC上时，求证：E为AB中点.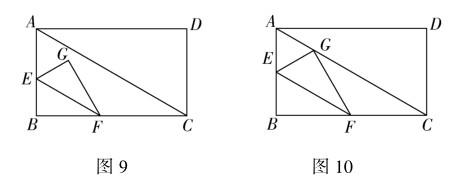

【设计思路】学生的“再创造”核心就是数学过程的再现，实际上就是一个“做数学”的过程.显而易见，学习数学，要不断地“往里走”，要会解题.本活动中教师带领学生一起读题并适当提问引导学生思考，结合所学的筝形性质来解题，还说明了读题，不能只看文字，要深入思考，探究本质.

四、课堂小结

师生互动：

1.本节课我们学习了筝形的哪些性质？你是从哪些方面来研究的？还学到了哪些数学方法？来谈谈你的感受.

2.现实生活中，你还发现哪些物品和筝形有密切联系？

【设计思路】课堂最后，教师根据学生的回答将一节课的内容再次联系起来，进一步促进了学生的深度学习.

结 语

“探索筝形”这节课作为“矩形、菱形、正方形”之后的补充，让学生认识了新的图形，了解了筝形的性质和特点.对学生而言，整节课中他们有体验、有经历，并在一个个问题中通过不断思考获得进步.这也证实了学生学习数学既要会静态推理，还要会动态操作；既要解决内部问题，还要解决外部问题，学数学，就要学身边的数学，学真实的数学，并服务于其他学科，最终将其应用到实际中创造更美好的生活！

【参考文献】

[1]董红峰.活动，让数学课堂教学变得鲜活[J].河南教育（教师教育），2022（7）：61.

[2]黄智灵，陈鑫荧.基于深度学习的初中数学活动课教学设计[J].福建中学数学，2022（4）：32-34.

[3]高婧婧.基于课标的初中数学课堂说数学教学活动研究[J].中学数学，2022（6）：92-93.

[4]张维蓉.利用探究活动提高数学课堂教学有效性的尝试[J].新课程研究，2022（25）：114-116.

[5]吴炳兴.教学活动在初中数学课堂中的应用探究[J].教育界，2021（43）：8-10.