火箭发动机涡轮泵故障检测及预测算法研究

王姝淇，刘梓琰，王 冠，陈海宝

(1.上海交通大学，上海 200240；2.北京宇航系统工程研究所，北京 100076)

0 引言

在液体火箭发动机中，涡轮泵是用于输送推进剂的核心部件，被称为液体火箭发动机的心脏，火箭发动机的多数故障都与它有关，振动则是涡轮泵故障的重要起因之一。涡轮泵工作转速高、工作环境复杂恶劣，易发生组件断裂、烧蚀等问题，造成严重后果。因此有必要研究高效的火箭发动机故障检测、故障识别方法，保障火箭的安全性与可靠性。

由于火箭发动机系统的复杂性，构建基于物理模型的方法十分困难，而近年来，随着深度学习及计算能力的发展，数据驱动的方法取得了广泛的应用。Zhang等[1]设计了一种基于端到端的深度学习模型，利用振动信号实现轴承故障诊断分析；马俊添等[2]通过深度残差网络结合时空卷积网络构建健康因子完成轴承剩余寿命预测；Hong等[3]使用小波包分解提取衰减过程，并使用经验模态分析算法提取波形趋势，共同处理振动信号的时频域特征，最后用自组织神经网络进行健康预测；Guo等[4]利用卷积神经网络(Convolutional Neural Network，CNN)构建了健康因子；Ren 等[5]结合了时域特征和频域特征，并提出频谱分割求和方法提取了退化趋势。

为了进一步揭示机械的退化过程，通常基于监测信号来构建健康指标(Health Index，HI)，用以表征机械的健康状态。HI的构建有不同的方式，如Huang等[6]、Hu等[7]通过RMS进行了滚动元件轴承的剩余使用寿命(Remaining Useful Life，RUL)预测；Li等[8]通过计算信号的数学形态模式谱构建HI；Hu等[9]通过计算旋转谐波振幅的平均对数比来监测齿轮的损伤过程。另外，通过融合多个物理特征构建HI模型的方法取得了广泛的应用，如Guo等[10]基于循环神经网络(Recurrent Neural Net-work，RNN)构建了用于轴承的RNN-HI，并进行了后续的RUL预测；Malhotra等[11]通过一个包含编码器-解码器的长段时间记忆网络(Long Short Term Memory，LSTM)构建HI。

基于上述综述方法，本文首先构建时频混合特征集及精简特征集，提出了基于特征集的故障预测方法和HI模型，以及基于时频谱图异常谱线的故障检测方法。

1 数据描述

本文使用的数据为某型液体火箭发动机试车数据。全部试车数据覆盖共计9台发动机29次试车试验，每次试车提供一个包含大量测量参数的数据集，参数可分类为缓变数据(如氧涡轮出口压力、燃气发生器室压等)、速变数据(如氧涡轮轴向振动、氧泵轴向振动等)。各次试车的基本状态统计如表1所示，其中试验编号方式为发动机编号-该发动机试车次数，如09-1代表9号发动机第一次试车(后文对发动机统一表述为xx号发动机，对试车试验统一表述为xx-yy次试车)，时长代表该次试车试验点火时间长度，健康状态与故障模式代表该次试车后发动机的状态，由试车试验后拆机检查得到，健康状态为无法判断的则代表未拆机检查，可能正常也可能故障。

由于振动信号具有响应快、敏感、特征丰富的特点，本文主要对其中的振动数据进行分析。数据中振动参数共有9个：氧泵壳体轴向振动、氧泵壳体径向振动、氧泵壳体切向振动、氧涡轮轴向振动、氧涡轮径向振动、氧涡轮切向振动、泵后支座轴向振动、泵后支座径向振动、泵后支座切向振动。

实际数据记录中并非所有参数均有记录，考虑到希望覆盖更多次试车，本文中的特征集构建采用各次试车的共有振动参数：氧泵壳体轴向振动、氧泵壳体径向振动、氧泵壳体切向振动，而故障预测方法和HI模型方法均基于特征集完成；而时频谱图的异常检测采用具有异常谱线特点的氧涡轮轴向振动、氧涡轮径向振动、氧涡轮切向振动数据。

2 特征集构建及精简

航天发动机是一个高度复杂的精密系统，而实际测量的振动数据包含大量无用信息，混杂着固有振动频率、零部件的振动、故障缺陷引起的振动、环境噪声，因此需提取混合信号中的有效特征。下面首先构建时域频域统计特征集[12]，并通过特征矢量降维对时频域特征集进行精简。

2.1 时频混合特征集

从时域、频域两方面分别进行统计特征集的计算，混合后形成完整的时频混合特征集。

2.1.1 时域特征集

时域分析根据传感器采集到的振动信号在时间域上的统计特征作为输入特征。通常通过对时域信号切片，计算切片窗口内的统计特征来代表该切片的特征，以此进行数据降维。目前，常用的时域特征及相应计算公式如表2所示。

表2 时域特征集构成Tab.2 Time-domain feature set

另外，不同监测数据表示不同的物理特性，具有不同的量纲和数量级，为消除数据不规范对效果的影响，进一步对特征集进行归一化处理。

2.1.2 频域特征集

振动信号包含各类要素信息，不同要素通常对应于不同频段的信号，可通过分析频域特征抽取所需的故障要素。信号经过傅里叶变换后，得到的各频率的幅值大小，对该频域信息做统计特征的分析作为频域特征提取，常用的频域特征如表3所示。与时域特征集构建类似，完成频域特征集构建后，同样须要对其进行归一化处理。

表3 频域特征集构成Tab.3 Frequency-domain feature set

分别按照表2与表3所示的特征，构建氧涡轮泵轴向、径向与切向振动3个参数的特征集，每个参数11个时域特征，12个频域特征共计23个特征。将上述3个参数特征混合在一起，形成69维时频特征集，用于生成第3章算法所需的精简特征集以及第5章HI模型构建算法的输入。

2.2 精简特征集

上述69维时频特征集虽然可以从不同的方面反映发动机的状态，但特征总维度大，包含冗余信息。为了降低数据维度，采用主成分分析(Principal Component Analysis，PCA)方法来进行特征降维，从原始数据集中精简得到显著特征集。

PCA通过正交变换将可能存在相关性的变量重新组合成一组新的线性不相关的综合变量，以实现采用较少的综合变量来尽可能多地反映原来变量大部分信息的目的。2.1节中构建的69维特征集，经PCA计算后成为69维的正交特征，按每个特征的方差大小排序，可得到表4。其中单个成分方差贡献率为某主成分的方差与全部主成分方差和的比值，累积贡献率为前k个主成分方差贡献率的累加。PCA降维的有效性常用降维后主成分的累积贡献率来表示，如果前k个主成分的方差累计贡献率超过了85%，那么说明用前k个主成分去代替原来的n个变量后，不能解释的方差不足15%。

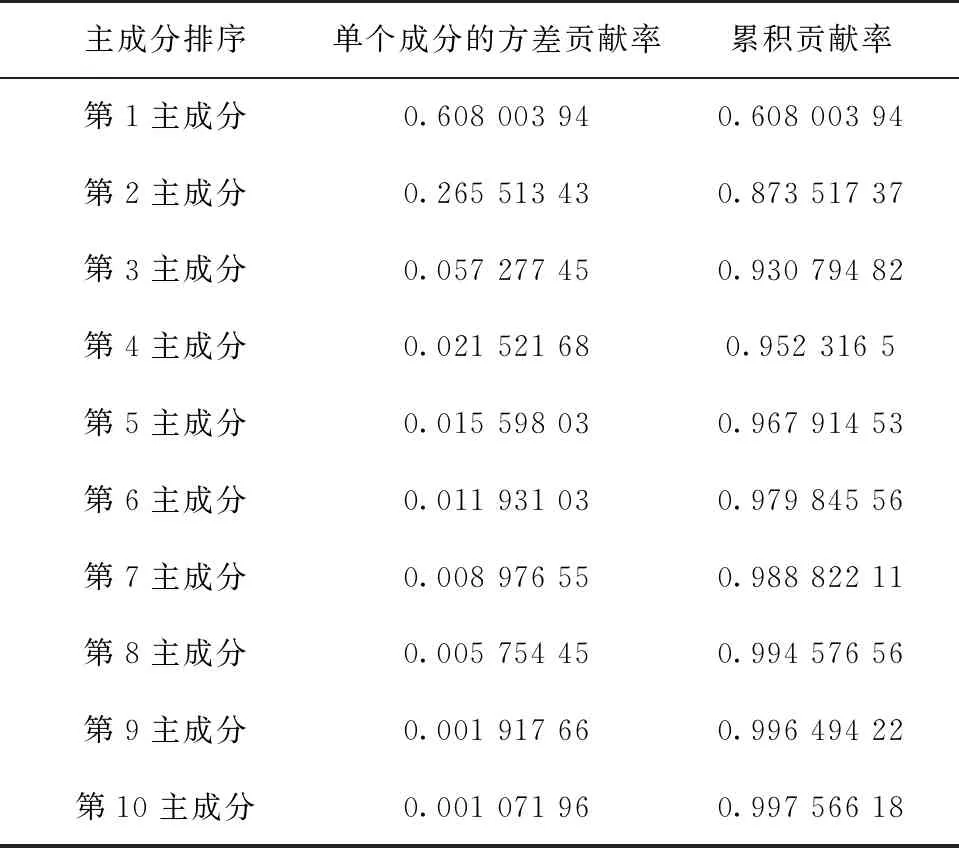
表4 69维特征集PCA主成分方差贡献率Tab.4 Variance contribution of principal component for 69 features

在氧泵轴径切的69维时频混合特征集中，前10个成分的方差贡献率及累积贡献率如表4所示。前4个主成分的累积贡献率达到了95%，而随着主成分的增加，累积贡献率上升逐渐缓慢。因此仅保留前4个主成分即可保留足够的信息量，将PCA后的前4个主成分作为精简特征集，用于故障预测方法。

3 基于精简特征集的故障预测方法

考虑火箭射前发动机短程试车的场景需求，因此本章开展故障预测方法研究，实现通过上一次试车数据预测下一次试车是否会出现异常的功能。该问题属于时间序列分类(Time Series Classification，TSC)问题。

根据Fawaz等[13]对传感器读数、光谱图、模拟数据等不同领域的数据集的实验结果，ResNet在时间序列分类上有出色的表现。ResNet通过调整模型结构，引入快捷连接的方式构建输出为F(x)+x的残差块，由该残差块叠加的网络更容易优化，能使网络层数大大加深。该结构如图1所示，上文中F(x)对应图中残差块输出中的W2·ReLU(W1·x)，其中W1和W2分别为两网络层的权重矩阵。

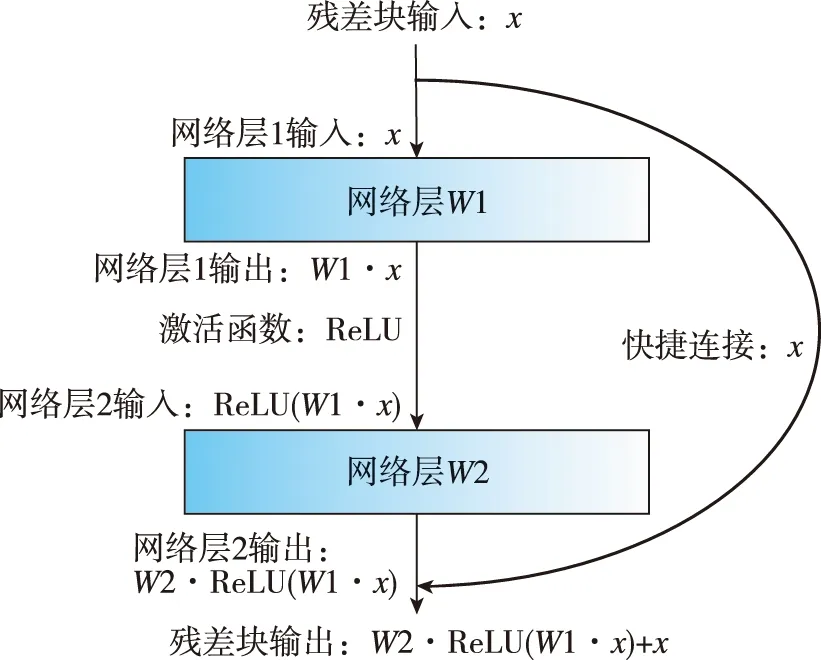
图1 ResNet网络残差块结构Fig.1 Structure of residual block

鉴于ResNet在时间序列分类问题的良好效果，这里也采用ResNet网络来完成，多维时间序列采用精简特征集，通过训练网络完成该特征序列到下一次试车预测结果的映射。网络结构如图2所示。

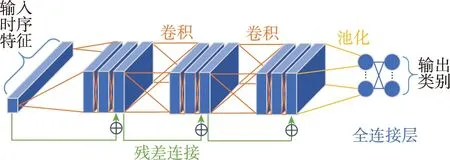
图2 残差结构的时间序列分类网络Fig.2 Classification network with residual structure

本章使用的数据为氧泵壳体轴向、氧泵壳体径向、氧泵壳体切向振动数据的精简特征集，将下一次试车的“正常”或“异常”情况作为当前试车数据的训练标签。在全部29次试车的数据中，以异常试车结束的发动机由于没有维修，下一次试车必然也是异常的，因此标签为“异常”；而以正常试车结束的发动机，包括09-1、14-6、28A-6、33-2次试车，其下一试车状态未知，从而标签“未知”。将上述4个标签“未知”的试车去除后，剩余可用的数据共计25次试车。将25个可用试车随机划分为19个训练集试车和6个测试集试车。

为了增加样本量、并挖掘局部的特征，提升预测结果的稳定性，采用了时间切片处理和投票机制。时间切片和标签设置如图3所示，切片时长设置为100 s，切片的标签与当前试车的预测标签一致，即每个时间切片样本都对应着下一次试车的分解检查情况(正常：0；异常：1)，进而作为网络监督训练的输入信息。经过时间切片后的数据样本量分别为：训练集77个样本，测试集30个样本。

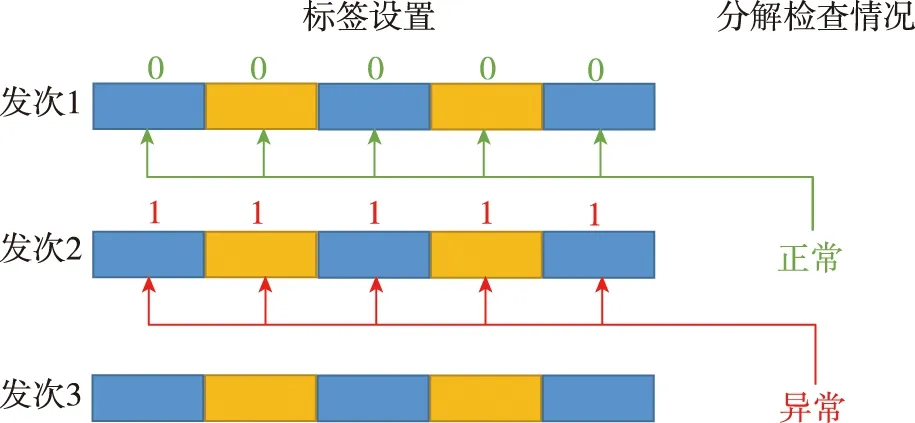
图3 时间切片和标签设置示意图Fig.3 Diagram of time slice and label setting

对于一个包含多个时间切片的试车，最终预测结果采用投票机制：当预测异常的切片数目多于正常时，认为综合预测结果为异常；当预测正常的切片数目多于异常时，认为综合预测结果为正常。最终预测结果以各个切片的综合结果来决定，以此提高预测的准确率和可靠性。

测试集预测效果如表5所示，对于测试集的6次试车预测均准确，最终效果准确率100%。值得指出，这里由于随机划分的因素，测试集均是500 s的试车长度，因此都是5个时间切片，实际上对于任意长度的试车可同理预测。

表5 测试集预测结果Tab.5 Prediction results on test dataset

4 基于时频谱图异常谱线检测的故障检测方法

前期研究表明氧涡轮泵试验中32号发动机的异常试车在氧涡轮轴向、氧涡轮径向、氧涡轮切向振动参数的时频谱图5 kHz附近呈现倾斜异常谱线的特点，而正常试车在该频段并没有出现倾斜谱线，且该情况在多台设备出现，因此推测时频谱图异常谱线，是判断氧涡轮泵异常与否的重要判据。

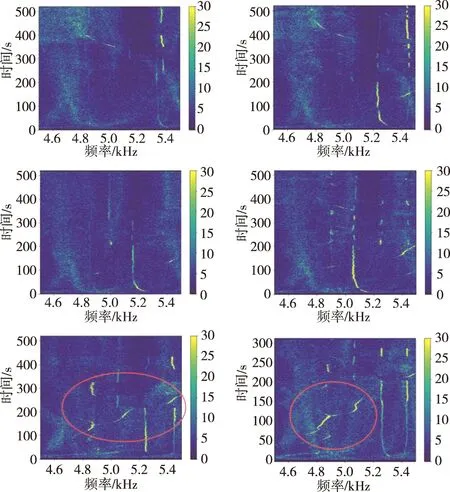
图5 氧涡轮径向振动时频谱图Fig.5 Time-spectrum diagrams of oxygen turbo pump radial vibration

本章针对时频谱图的异常谱线检测展开研究，采用的振动参数是氧涡轮轴向、氧涡轮径向、氧涡轮切向，采用32-1、32-2、32-3、32-4、32-5、32-6次试车。通过时频域分析绘制时频谱图，采用神经网络方法对时频谱图中的异常谱线进行检测，由此确定故障检测的目标。

4.1 时频谱图绘制

上述时域特征、频域特征是单独在时域或频域的分析，但考虑到信号的频率特性可能随着时间变化，为了捕获这一时变特性，时频域分析提供一种在时域和频域均有分辨率的分析方法。短时傅里叶变换是时频域分析的主要方法，其定义如下

(1)

式中，x(m)为输入信号，ω(m)为窗函数。通过短时傅里叶变换获得时间和频率的二维函数X(n，ω)，利用二维图像表示，即得到信号时频谱图。

前期研究表明，氧涡轮泵试验异常试车在时频谱图5 kHz附近呈现倾斜异常谱线的特点，因而重点关注5 kHz附近的频谱，同时放大频段4.5～5.5 kHz 绘制时频谱图。图4、图5、图6分别是32号发动机6次试车的氧涡轮轴向、氧涡轮径向、氧涡轮切向振动参数在5 kHz附近的时频谱图，由左至右，由上至下分别为32-1至32-6次试车。

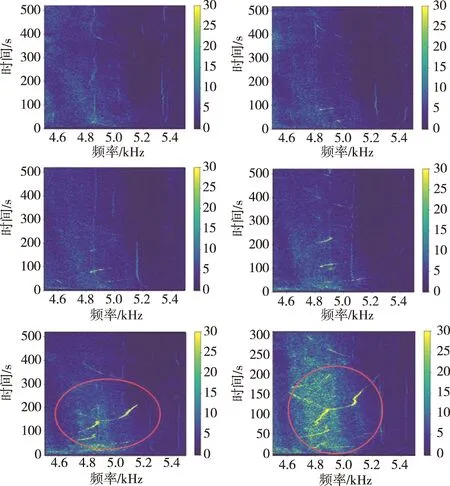
图6 氧涡轮切向振动时频谱图Fig.6 Time-spectrum diagrams of oxygen turbo pump tangential vibration

图4～图6中，32-1至32-4均表现出高亮竖纹特征，而32-5、32-6则表现出高亮斜纹特征(红圈标记处)，可见32号发动机的氧涡轮轴向、径向、切向振动数据在状态异常时均表现出相近的异常谱线特征，这为后续异常谱线识别分析检测奠定基础。

4.2 基于ResNet的故障检测方法

ResNet网络在图像特征提取方面具有较好的优势，本文将采用ResNet对时频谱图检测。为了挖掘小时间范围的异常谱线，将频段为4.5～5.5 kHz的时频谱图做每1 s的切片，如图7所示。

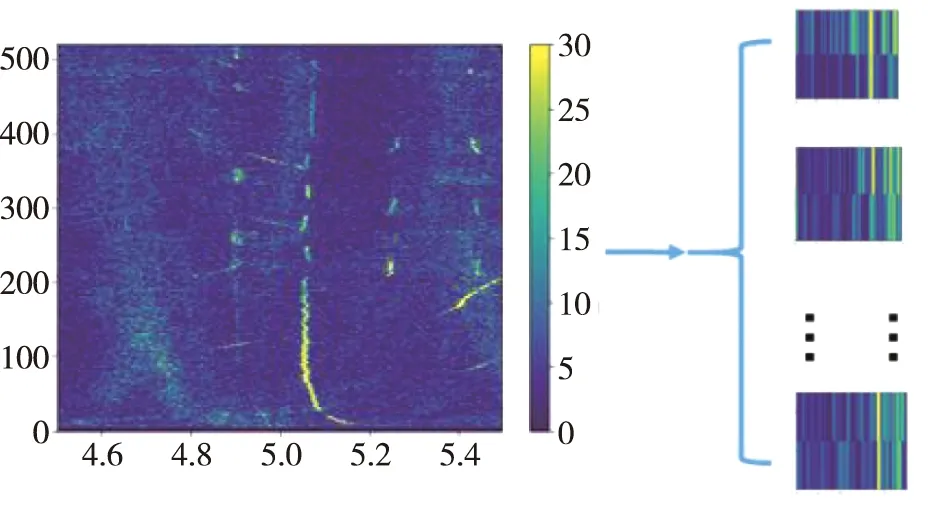
图7 局部时频谱图获取方法Fig.7 Method of obtaining local time-spectrum diagram

根据局部时频谱图中有无斜向谱线作为第一个训练标签，考虑到不同工况下的不同情况，使用工况作为第二个训练标签。类别标签，即有无异常，用1表示异常，用0表示正常；工况标签分别用0，1，2表示低、中、高工况。利用32-5和32-6次试车的氧涡轮轴向振动参数的时频谱图切片作为数据集，随机划分为训练集和测试集。将数据的局部时频谱图按秒切片，将每个切片图像转换成 (3，224，224)维度的数组，作为ResNet网络输入，以对应的类别标签与工况标签作为网络输出的期望。图8、图9分别展示了ResNet网络训练和测试的结果中，由每个局部时频谱图的1 s 时间切片样本经ResNet网络预测得到的类别与工况与其真实状态的对比情况，其中横坐标的值代表样本的序号，每个样本代表1 s时间切片的时频谱图。

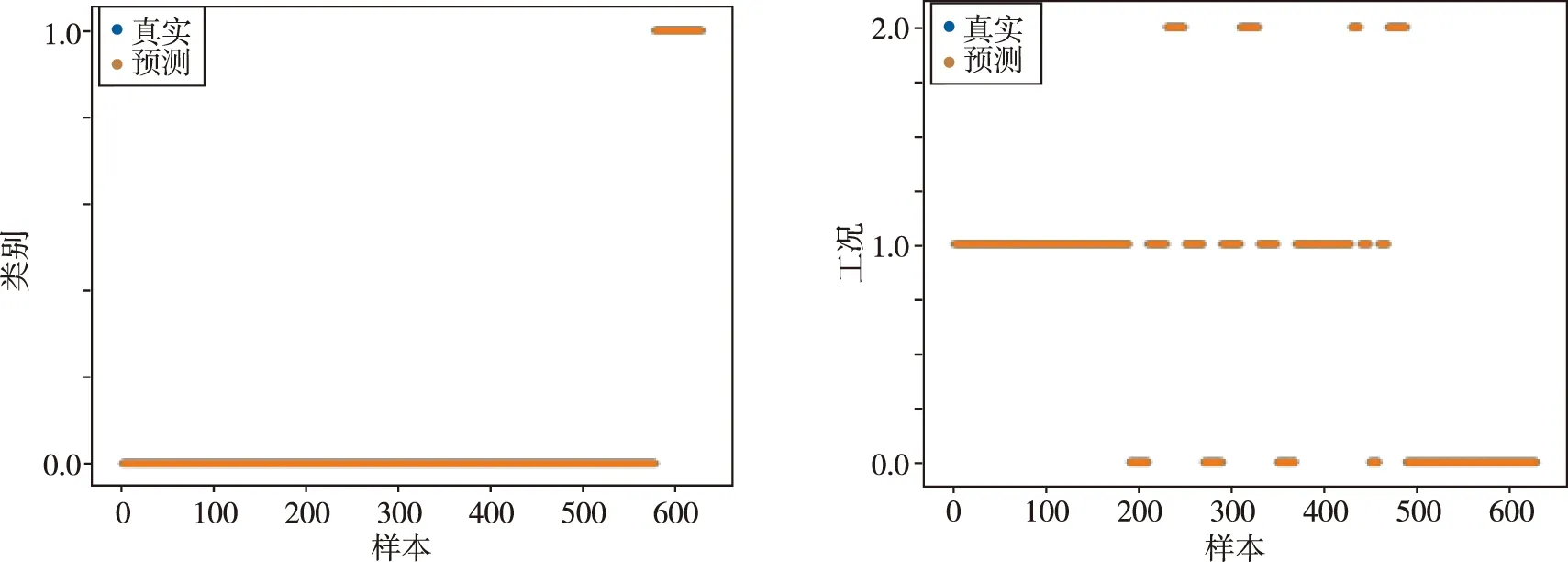
图8 训练效果Fig.8 Training effect

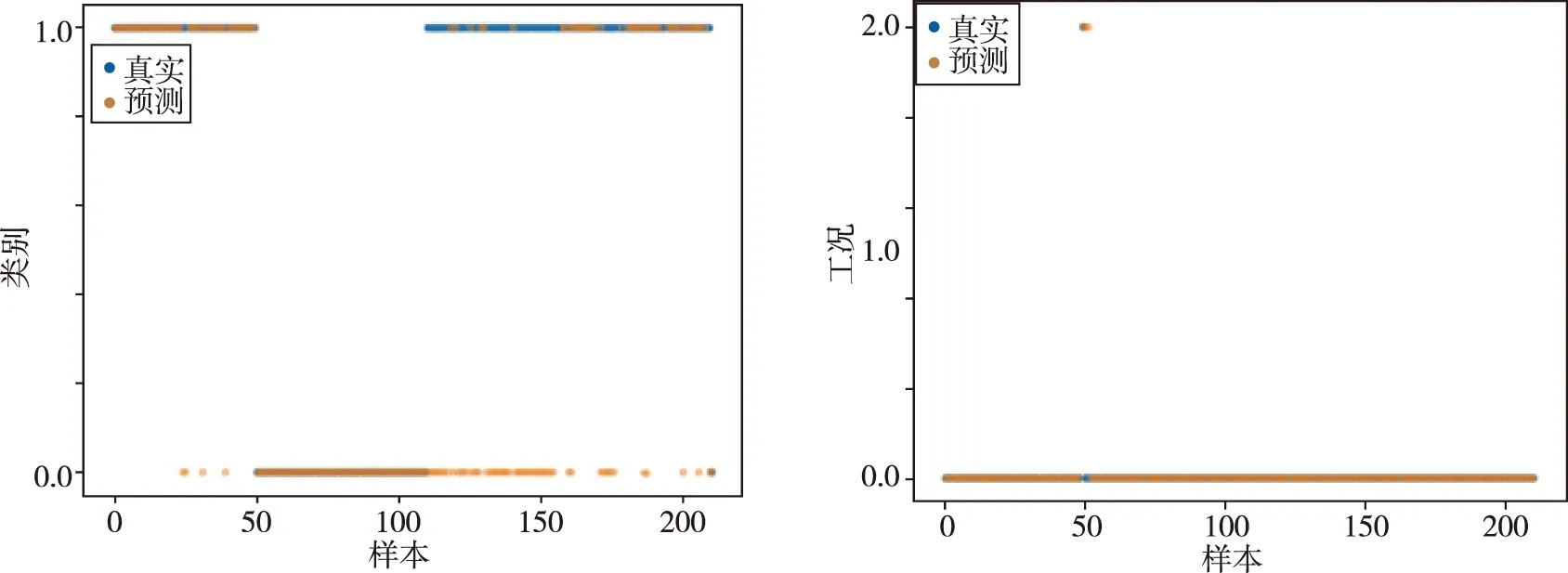
图9 测试效果Fig.9 Testing effect

图9表明了算法的测试结果，在每个横坐标对应的样本上，若橙色点与蓝色点重合则代表准确，反之则不准确，经过统计，在200余个测试样本中，异常谱线检测的准确率约77%，工况识别的准确率约为99%，证明了利用小样本数据进行故障诊断的可行性。

5 基于时频混合特征集的HI模型构建

为了为氧转子运行提供一个能够及时发现隐患的评价工具，应用上述构建的69维时频混合特征集来构建HI，该特征集的特征量较多，从而可以对HI有更好的拟合。本节使用包含19、32、21、28A、33、14、09号发动机共26次试车的数据，将试车数据按2.1节中方法构建的氧泵壳体轴向、氧泵壳体径向、氧泵壳体切向振动数据的69维完整时频混合特征集。

将同一个发动机不同次试车在去除不稳定的启动段后连接起来，模拟HI问题的连续运行到失效的数据形式，构建线性回归的HI模型。在目标HI退化曲线中最常用的、最成功的形式是指数衰减[14]，由于指数衰减模式的前期平缓、后期加速的模式更符合实际情况，如下式所示

ht=

(2)

式中，β代表起始为1的部分占总体的比例(也是末尾为0的部分占总体的比例)，L为数据长度。

在对HI进行拟合时，最常用的是线性回归方法[14-15]，逻辑回归会因扭曲系统原有的退化模式(如指数模式)而不适用[11]。为了保留信号/特征中的原始模式，采用线性回归模型对指数衰减进行拟合，线性回归模型为

(3)

式中，f(x)代表HI的值，x=(x1，x2，…，xN)是N维特征矢量，(α，β)=(α，β1，β2，…，βN)是N+1个模型参数，该模型完成从N维矢量到HI值的映射。根据表1，仅有19号发动机的6次连续试车是确定满足条件的从正常到失效的试车(19-1正常，19-2正常，19-3正常，19-4正常，19-5无法判断，19-6异常)，因此基于19号发动机建立损伤模型，拟合效果如图10所示。对存在异常的试车验证，其数据如表6所示。

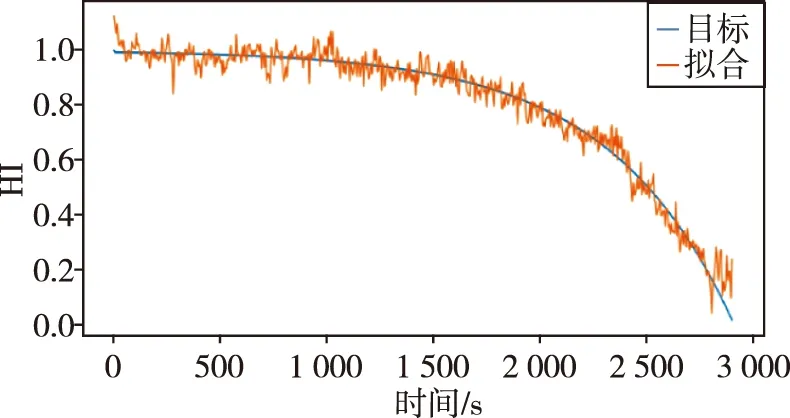
图10 19号发动机拟合效果Fig.10 Fitting effect of No.19 engine

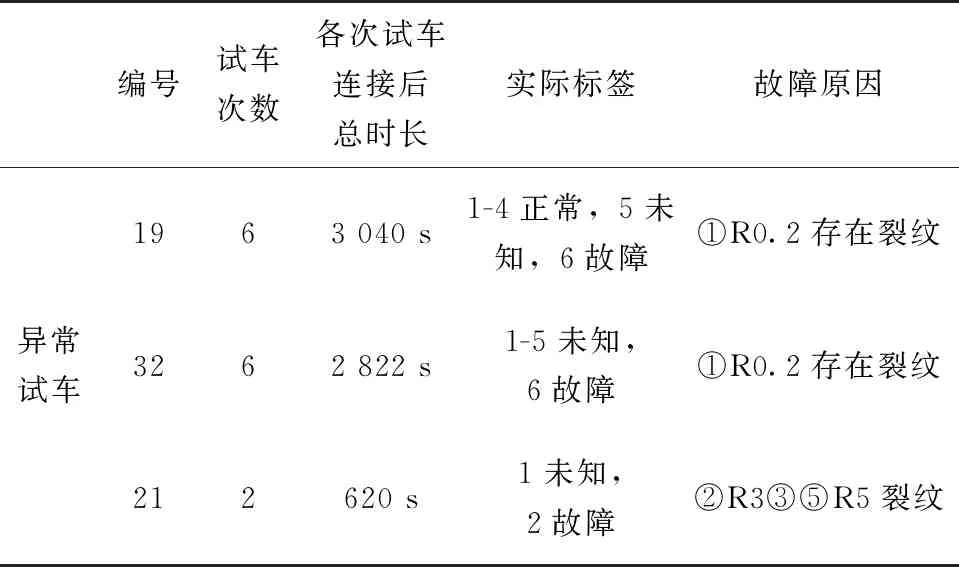
表6 异常试车数据详情Tab.6 Data information of abnormal operation

在跨发动机验证时，模型输出结果体现出扰动较大、毛刺较多的情况，为了更好地判断曲线趋势，还对模型输出结果曲线进行平滑降噪处理，通过S-G滤波降低噪声干扰，放大趋势性的变化，降噪后体现为结果图中的橙色曲线。

对于异常的32和21号发动机验证如图11所示。由图11可以看出，32号发动机前面健康值一直较高，但在末尾体现出明显的衰退趋势，表明32号发动机在末尾有明显退化趋势，对应着32-6次试车可能存在异常，这与32-6次试车的实际标签相符合；21号发动机在末尾也存在明显的健康衰退趋势，因此认为其存在异常，这与21-2次试车的实际标签符合。另外，参考表1，24与34号发动机，各自仅有一次时长为100 s的试车，且事后检查存在故障。对于这类发动机该方法并不适用，这是由于经过数据预处理和特征提取后的数据长度非常小，构建的HI曲线可能完整地处于异常状态，难以观察到退化趋势，而各类试车故障模式，对应故障状态的HI不同，没有趋势仅观测数值难以进行判断。

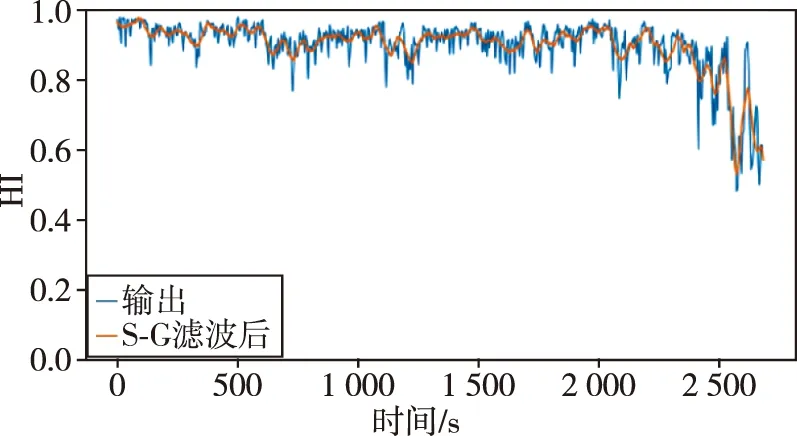
(a)32号发动机

对于正常发动机的HI趋势曲线如图12所示，分别是28A、33、14、09号发动机，可见均未表现出健康值的下降趋势，没有显著的退化特征，其中33号发动机构建的HI曲线时间长度短，但计算得到的HI很高，因此也可以表征该发动机状态正常。

综上所述，在跨发动机验证中，异常发动机能够在HI曲线中表现出明显的下降趋势，表征了健康状态的衰退；而正常发动机未表现出健康值的下降趋势，没有显著的退化特征。证明该方法可以对涡轮泵健康状态进行有效评估。

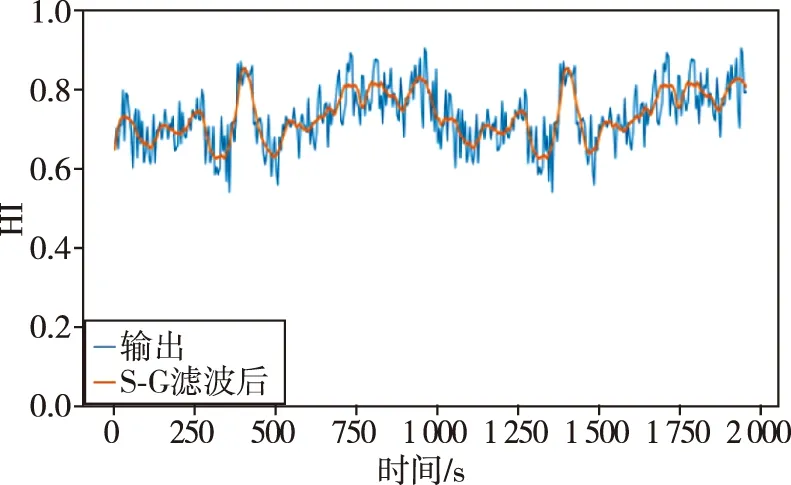
(a)28A号发动机

6 总结

本文提出了针对某型液体火箭发动机涡轮的故障预测、故障检测与健康状态评估方法，并在真实火箭发动机数据集上进行了测试验证。在故障预测方面，基于精简特征集和ResNet实现了对下一次试车正常或异常的预测，引入时间切片的方法，最终达到100%的预测准确率。在故障检测方面，通过时频域分析对于时频谱图中的重点关注频段体现出的异常谱线与异常之间存在的关联问题，设计ResNet网络来实现对于异常谱线的识别，达到了较好的识别准确率。在健康状态评估方面，通过设立的经验退化趋势函数和时频混合特征集拟合试车数据实现健康评估，并在发动机涡轮泵数据进行测试，验证该方法可以量化表征涡轮泵健康状态。