无筋超高性能混凝土板的受弯性能及承载力计算

苏捷，陈俊廷，方志，3†，陈佳醒，曹清，周腾

［1.湖南大学 土木工程学院，湖南 长沙 410082；2.绿色先进土木工程材料及应用技术湖南省重点实验室（湖南大学），湖南 长沙 410082；3.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南 长沙 410082；4.广东省交通规划设计研究院集团股份有限公司，广东 广州 510507］

超高性能混凝土（Ultra High Performance Concrete，UHPC）以其高强、高韧和高耐久性等特征有望在工程结构中得到广泛应用［1-3］.由于基体内钢纤维的存在，即使不配置钢筋，UHPC 受弯构件受拉区的钢纤维也可有效抑制裂缝的开展并使构件具有较高的抗弯承载力［4-7］.采用无筋UHPC可使结构轻薄、易于成型并大幅简化施工［8-9］，因此无筋UHPC 板在国内外非重载的板壳结构中得到较广泛的应用.如国内多条高速铁路或客运专线上使用的无筋UHPC 人行道板、电缆槽盖板和轨道板［10-13］；Shawnessy 轻轨车站采用了板厚仅为20 mm 的无筋UHPC 薄壳屋盖［14］；Millau Viaduct 收费站使用无筋UHPC 建造了面积达2 800 m2的屋盖［15］.

国内外学者对无筋和配筋UHPC 板的受力性能进行了研究.余自若等［4］对5 块钢纤维掺量为3.5%的无筋UHPC 单向板进行了受弯试验，发现板在开裂后仍能承担较大的荷载；Duque 等［5］对18 块钢纤维掺量为2%的无筋UHPC 单向板进行了弯曲破坏试验，发现相比于钢纤维取向垂直板带方向的试件，钢纤维取向沿板带方向试件的受弯承载力提升约1.4 倍；Harris［16］对12 块钢纤 维掺量 为2%的无筋UHPC 方板进行了局部加载试验，其中5 块板发生受弯破坏、7 块板发生冲切破坏，确定了避免发生冲切破坏的临界板厚；樊健生等［17］对11 块钢筋UHPC 单向板进行了局部加载试验，基于塑性极限法提出了配筋UHPC 单向板的抗弯承载力计算方法；Zohrevand 等［18］对局部后浇钢筋UHPC 方板进行了局部加载试验，发现利用塑性铰线法能较好地预测板的抗弯承载力；周凯［19］对10 块局部后浇钢筋UHPC 方板进行了冲切试验，发现UHPC 的加入能使板由脆性的冲切破坏转为延性的弯曲破坏；方志等［20］对9 块局部荷载作用下钢筋UHPC 方板的抗冲切性能进行了试验研究，提出了可考虑局部荷载作用位置影响的抗冲切承载能力计算方法.目前对于无筋UHPC单向板的受力性能研究较多，但鲜见关于无筋UHPC方板抗弯性能的研究报道.

预测UHPC 受弯构件的抗弯承载能力时，宜考虑截面受拉区UHPC 的抗拉作用以反映UHPC 较高抗拉强度的有利作用.为简化UHPC 构件的抗弯承载力分析，一般将极限状态时截面受拉区较复杂的拉应力分布等效为矩形分布来计入UHPC 的抗拉作用，其应力大小为kft，ft为UHPC 的抗拉强度，k为受拉区等效均布应力折减系数.杨剑等［21］基于9 根配筋UHPC 梁的弯曲性能试验结果，建议k取0.5；刘超等［22］基于5根配筋UHPC梁的弯曲破坏试验结果，建议k取0.9；瑞士超高性能混凝土设计指南建议k取0.9［23］；彭飞等［24］分析了配筋率、梁高、钢纤维长度和预应力水平等参数对配筋UHPC 梁系数k的影响，提出了考虑构件尺寸效应影响的系数k的取值方法.现有关于构件受拉区UHPC 等效均布应力折减系数k的研究主要集中在配筋的梁式构件且其取值范围变化较大.

不同于UHPC 梁式构件中钢纤维的三维分布，UHPC 薄板中的钢纤维更趋向于二维分布状态并有利于构件弯曲性能的改善［25］；不同于配筋UHPC 梁的极限状态一般由受压区UHPC 达到其极限应变控制，极限状态时无筋UHPC 板受压区应力将远低于其抗压强度，板的破坏通常由受拉区UHPC 达到其极限拉应变所控制，因此钢纤维的影响会更趋显著［26］，受拉区UHPC 等效均布应力折减系数k的取值亦可能会有所不同.

基于此，本文首先对无筋UHPC 单向板和方板分别进行弯曲破坏试验，以期明确相应的受力破坏特征；再基于UHPC 的轴拉试验结果，提出不同钢纤维掺量UHPC 的受拉应力应变关系并用其对单向板的受弯性能进行数值分析，以期确定UHPC 受拉区等效均布应力折减系数k的合理取值，并建立无筋UHPC单向板截面抗弯承载力的简化计算方法；最后依据方板的破坏特征选取合理的破坏机构对其进行塑性极限分析，以期明确塑性铰线法确定无筋UHPC方板极限承载能力的适用性.

1 试验概况

1.1 试件设计

设计和制作了无筋UHPC 单向板和方板各1 块.单向板试件尺寸（长×宽×厚）为900 mm×430 mm× 60 mm，方板试件尺寸（长×宽×厚）为900 mm× 900 mm×80 mm，计算跨径均为800 mm，如图1 所示.其中方板试件采用了较大的板厚（80 mm）和较小的跨厚比（1/10），以使板在集中荷载作用下发生期望的受弯破坏而非冲切破坏.

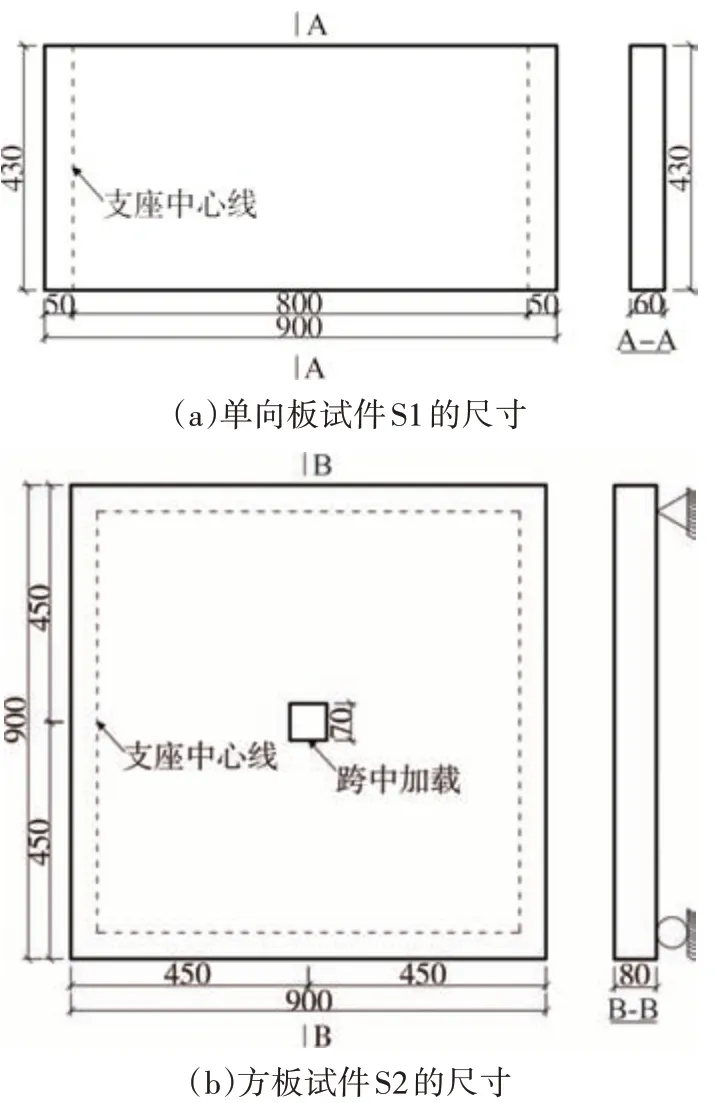
图1 截面尺寸（单位：mm）Fig.1 Dimension of section（unit：mm）

1.2 材性试验

试件所用UHPC 材料为商品预混料.配合比（质量比）见表1.UHPC 中所掺钢纤维为镀铜平直钢纤维，体积掺量为2%，直径为0.2 mm、长度为13 mm、长细比为65，抗拉强度大于2 000 MPa.

表1 UHPC配合比Tab.1 Mixture ratios of UHPC

依据《活性粉末混凝土》（GB/T 31387—2015）［27］，立方体抗压强度采用边 长100 mm 的立方体进行测量，棱柱体抗压强度和弹性模量采用100 mm×100 mm×300 mm 棱柱体测量，抗折强度采用100 mm× 100 mm×400 mm 棱柱体测量；UHPC 轴拉性能参考《超高性能混凝土基本性能与试验方法》（T/CBMF 37—2018）中建议的狗骨头形状试件确定［28］，如图2 所示.实测UHPC 的抗压强度、抗折强度、抗拉强度和弹性模量见表2.

表2 实测UHPC的性能Tab.2 The measured properties of UHPC

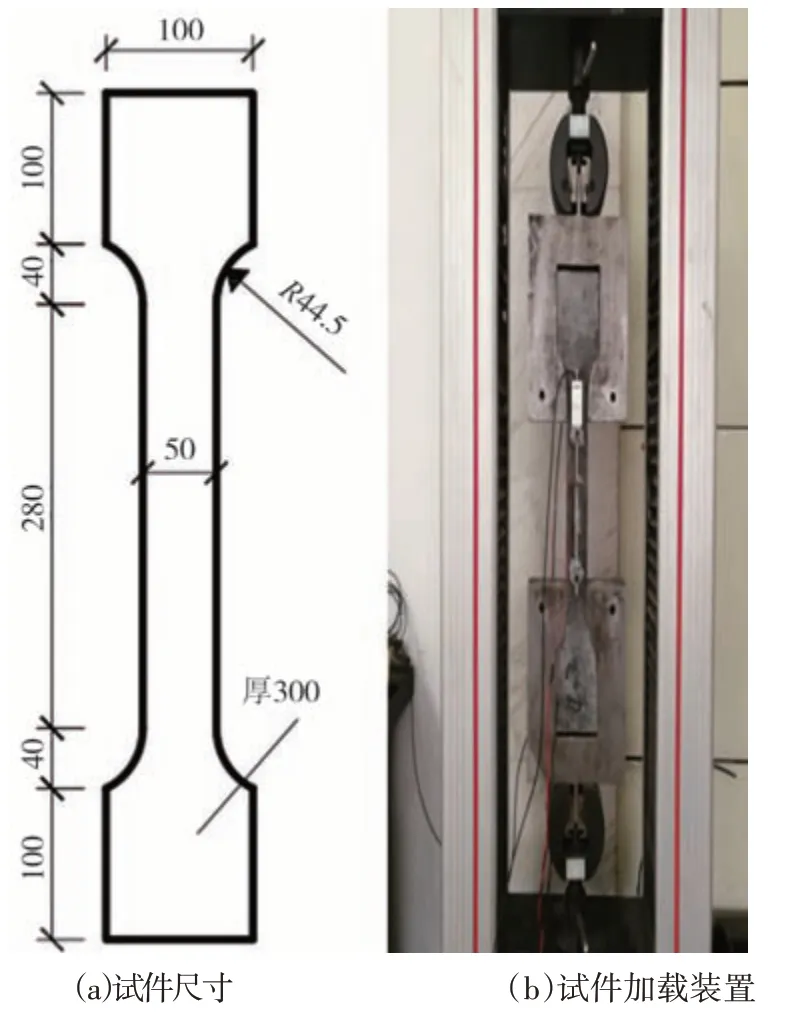
图2 轴拉性能试件尺寸及加载装置（单位：mm）Fig.2 Axis tension specimen dimension and loading device（unit：mm）

1.3 加载方式与测点布置

单向板一端为固定铰支座，另一端为滑动铰支座；方板相邻两边的支承为固定铰支座，另外两边为滑动铰支座以实现方板的四边简支.由50 t 液压千斤顶进行加载，采用压力传感器测定荷载大小.如图3（a）所示，单向板加载装置中借助横向分配梁及其下方宽10 cm的矩形橡胶垫块实现跨中横向线荷载的施加；如图3（b）所示，方板加载装置中千斤顶下放置钢制球铰以保证加载方向垂直于试件表面，板跨中局部加载板边长为70 mm×70 mm，加载板下放置与加载板大小一致的橡胶垫块以保证荷载由加载钢板均匀传至试件.

图3 加载装置Fig.3 Loading derice

试验采用分级加载.峰值荷载前采用力控制加载，峰值荷载后改为位移控制加载，当荷载下降至峰值荷载的85%时终止加载.板的实测抗弯承载力均取峰值荷载.

采用百分表测量试件加载位置和支承中心处的竖向位移，单向板跨中截面左、右两侧对称位置设2个位移测点；在单向板试件跨中沿截面高度布置应变片以测量截面的应变分布，在方板试件顶面沿加载板周边布置应变片以测试板顶不同位置的混凝土应变.测点布置如图4所示.

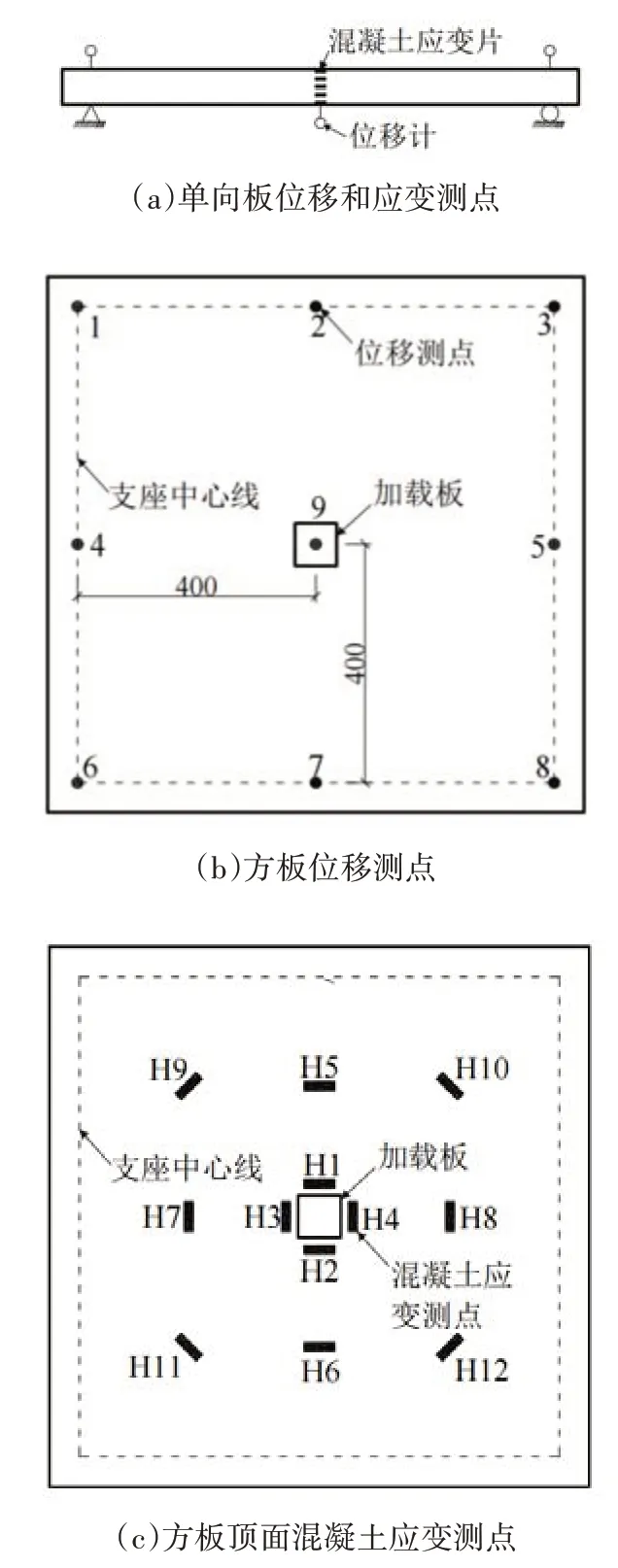
图4 测点布置（单位：mm）Fig.4 The measuring point layout（unit：mm）

2 试验结果及分析

2.1 UHPC轴拉性能

不同钢纤维掺量UHPC 轴拉性能试验结果如 表3 和图5 所示.定义图5 所示轴拉应力-应变曲线初始线性上升段末端的转折点为基体开裂点或弹性极限点，对应的应力和应变分别为初裂应力σte和初裂应变εte，斜率为弹性模量Ec；受力过程中经历的最大应力点为峰值点，对应的应力和应变分别为峰值应力σtp和峰值应变εtp；峰值应力点后应力下降至峰值应力85%处的点定义为极限点，相应的应力和应变称为极限应力σtu和极限应变εtu.基体开裂点、峰值点和极限点间的曲线近似呈线性变化.不同于不含钢纤维的素UHPC 开裂后即断裂，即使1%钢纤维掺量的UHPC，基体开裂后仍能继续耐受变形，但曲线呈现软化特征；当钢纤维掺量增加到2%时，基体开裂后表现出应变强化特征.基于文献［29］及本文试验结果，分别采用如图6 所示的双折线和三折线来描述应变软化和硬化UHPC的轴拉应力应变关系.

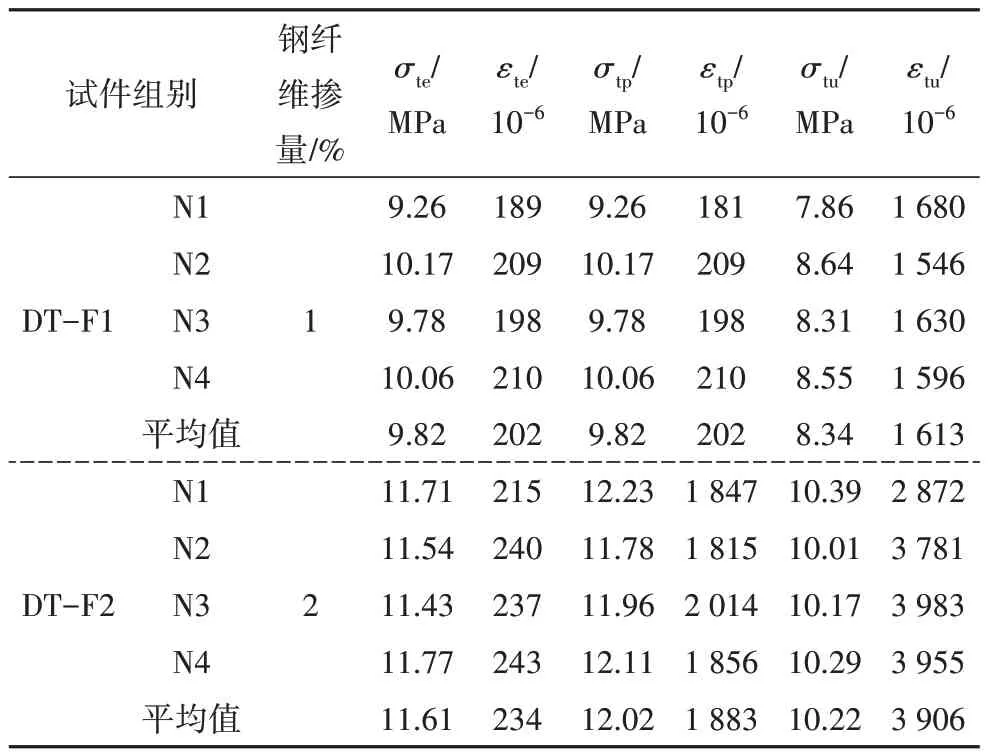
表3 UHPC轴拉性能试验结果Tab.3 Test results of UHPC under axial tensile

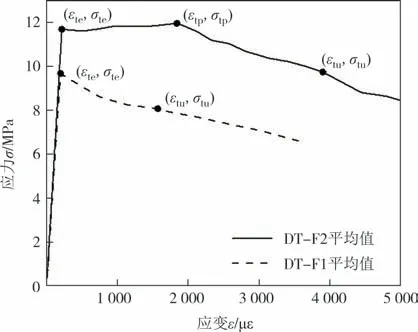
图5 不同钢纤维掺量UHPC轴拉应力应变关系Fig.5 Axial tension stress-strain relationship of UHPC with different steel fiber content

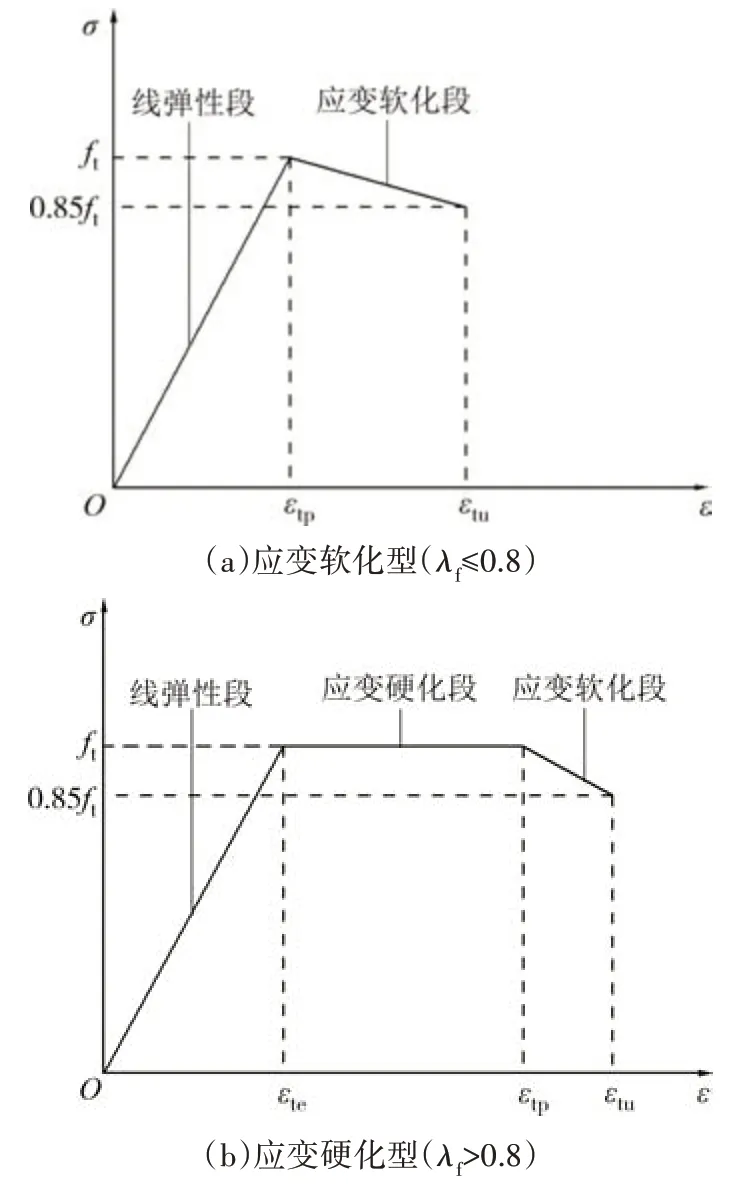
图6 UHPC轴心受拉本构关系Fig.6 Constitutive model of UHPC under axial tension

采用纤维特征参数λf［如下述式（4）］来描述钢纤维对UHPC 抗拉性能的影响［30］.为明确纤维特征参数对图6所示UHPC轴拉应力-应变曲线中峰值应变εtp和极限应变εtu的影响，收集了国内外文献中的120 个UHPC 轴拉试验数据［4，29-39］，如图7 和图8 所示.样本试件的钢纤维掺量为1%～4%，纤维长度为9～25 mm，长径比为45～125，相应的钢纤维特征参数变化范围为0.65～2.6.从图中可以看到：当λf≤0.8 时，UHPC 表现为应变软化，峰值应变εtp即为初裂应变且 受λf的影响较小；当纤维 特征参数λf＞0.8 时，UHPC表现为应变硬化，其峰值应变则随纤维特征参数增大而接近线性增大；无论是应变软化型还是硬化型，极限应变εtu均随纤维特征参数的增大接近线性增加.基于试验结果，可确定图6 所示应力-应变曲线上各特征点的取值如式（1）～式（4）所示.

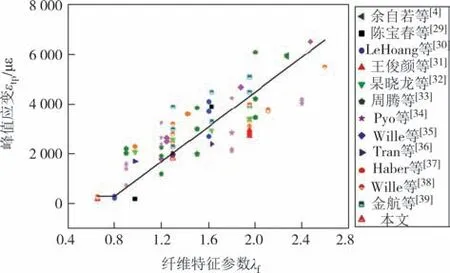
图7 峰值应变-纤维特征参数Fig.7 Peak strain-fiber characteristic parameter

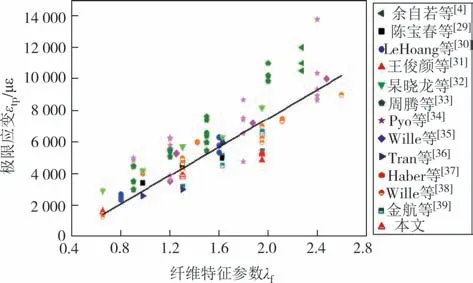
图8 极限应变-纤维特征参数Fig.8 Ultimate strain-fiber characteristic parameter

式中：εte、εtp和εtu分别为UHPC 轴拉弹性极限（初裂）应变、峰值应变和极限应变；ft为UHPC 的轴拉强度；ρf、lf和df分别为钢纤维的体积掺量、长度和直径.

图7 和图8 表明：基于式（4）所示的钢纤维特征参数，按式（2）和式（3）确定的UHPC 轴拉峰值应变和极限应变，在钢纤维规格参数处于样本数据所包含的范围内（长度9～25 mm，长径比45～125）时，尚能较好地反映试验结果的变化特征.但需要说明的是，当UHPC 中配置的钢纤维长度较短（lf＜9 mm）、长径比较小（lf/df＜30）时，仅依据钢纤维特征参数λf，不足以完全确定UHPC 的受拉变化特征，尚与钢纤维的长径比有关［40］.为此，需要确定式（2）和式（3）适用的钢纤维长径比.

日本JSCE 相关规程建议［41］UHPC 中钢纤维长度取值范围为10～20 mm，直径为0.1～0.25 mm，长径比一般为40～100［41］；国内相关规程建议UHPC 中的钢纤维规格为：直径0.12～0.2 mm，长度8～20 mm，长径比一般为60～100［42］；工程实际中，常用钢纤维的长度、直径和长径比一般分别约为13 mm、0.2 mm和65.

参考国内外相关技术规程的规定及工程实际常采用的钢纤维规格，规定所提UHPC 受拉本构适用的钢纤维长径比为40～100，且这一取值范围亦包含在回归式（2）和式（3）所用的样本数据范围内.

2.2 UHPC板的抗弯性能

2.2.1 破坏形态

图9是单调加载下单向板试验结束后的板底裂缝形态.开裂荷载时，板底面首先出现2条短细裂缝，其宽度约为0.03 mm；继续加载，裂缝宽度和数量逐渐增加，裂缝逐渐延伸至板边，其中一条裂缝发展较快形成主裂缝；峰值荷载时，主裂缝宽度增至0.43 mm，随后试件较快丧失承载能力而破坏.板底裂缝较多，平均裂缝间距约为5 cm.由于板底线性支座欠平整或板顶条形荷载沿板横向施加欠均匀，因此板内存在一定的扭转作用，使得如图9 所示板底横向裂缝走向与支座中心线或条形加载板纵向有所偏离，但偏离较小，板最终仍然发生期望的弯曲破坏，且板开裂后跨中截面左、右两侧对称位置处的实测位移增量相近，表4 中挠度值取为两侧位移实测值的平均值，以尽可能消除实测结果中扭转产生的影响.

表4 UHPC板试验结果Tab.4 Test results of UHPC slabs

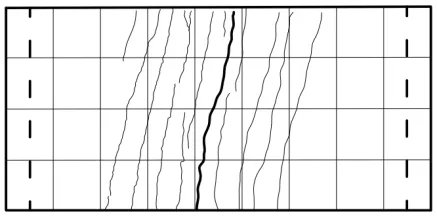
图9 UHPC单向板破坏形态Fig.9 UHPC one-way slab failure mode

图10 是单调加载下方板试验结束后的板底裂缝形态，主裂缝近似呈“十”字形.加载到开裂荷载时，板底跨中位置出现两条纵、横交叉的短细裂缝；继续加载，裂缝逐渐加宽并向板边延伸，同时裂缝出现分叉；峰值荷载时，两条主裂缝扩展至板边缘，形成纵、横通长裂缝，随后试件也较快丧失承载能力，破坏时板底裂缝较少.

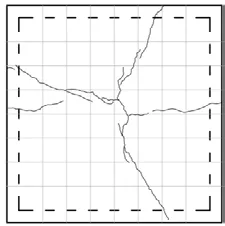
图10 UHPC方板破坏形态Fig.10 UHPC square slabs failure mode

2.2.2 荷载-挠度曲线

两类试件的荷载-挠度曲线及曲线各特征点的数值分别如图11 和表4 所示，试件受力均可分为弹性阶段、裂缝发展阶段和失效阶段.

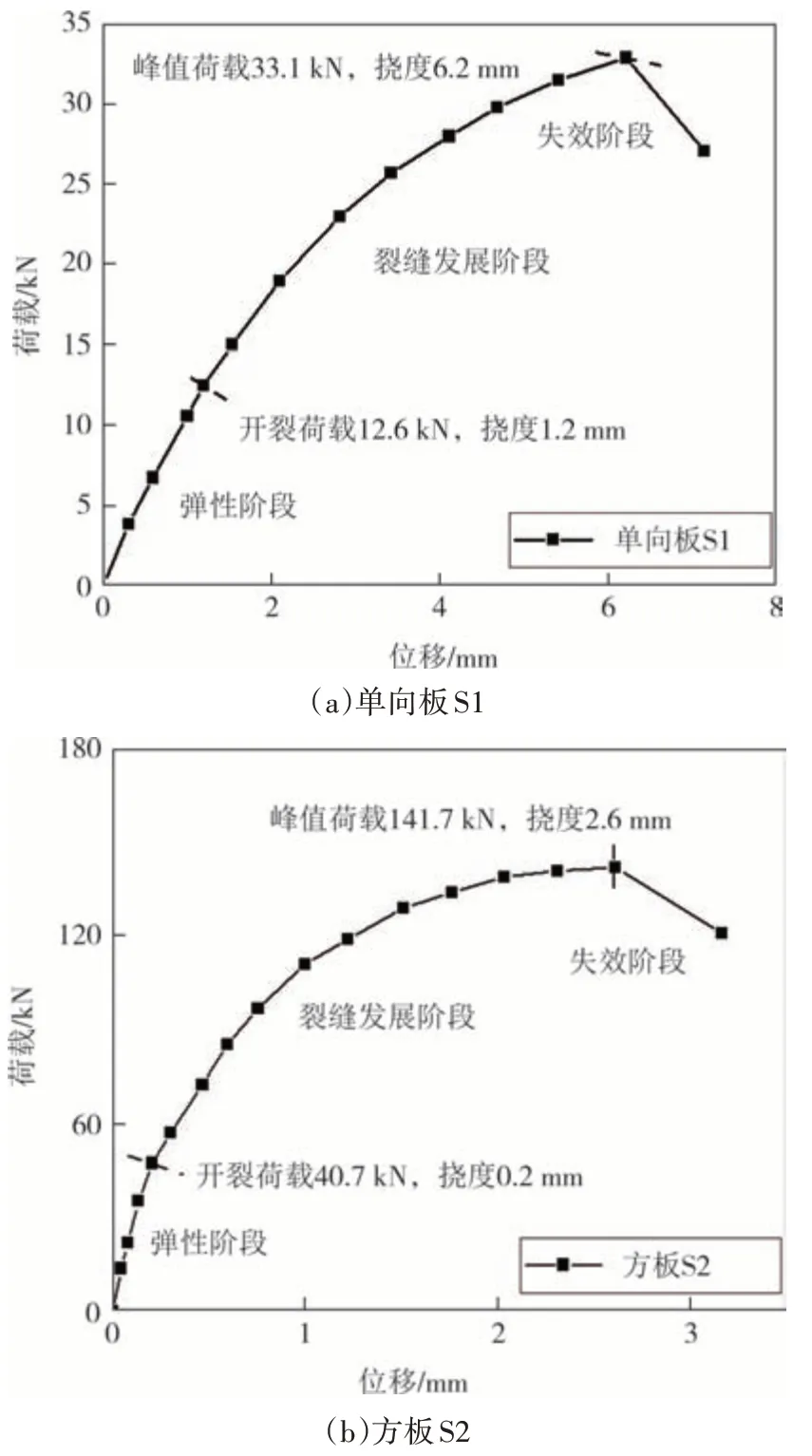
图11 荷载-跨中挠度曲线Fig.11 Load-midspan deflection curves

1）开始加载到基体开裂为弹性阶段.荷载与挠度呈线性关系，开裂荷载时，板底受拉区UHPC 达到材料的初裂应变，试件出现裂缝.单向板和方板试件的开裂荷载分别为峰值荷载的38.1%和28.7%.

2）基体开裂到峰值荷载为裂缝发展阶段.荷载-挠度曲线呈现非线性特征，试件刚度逐渐降低，加载过程中可听到钢纤维被拔出的响声，主裂缝逐渐形成.定义峰值荷载和开裂荷载时的挠度比为延性系数，则单向板和方板试件的延性系数分别为5.2 和13.0.可见：超静定方板内存在的弯矩重分布过程，可使方板的延性得以明显加强.

3）峰值荷载后为失效阶段.峰值荷载后，伴随更明显的纤维拔出响声，钢纤维的桥接作用快速退化，曲线进入下降段，试件因主裂缝快速发展而破坏，但受压区UHPC较加载前无明显变化.

实际上，无筋UHPC单向板的抗弯承载力本质上反映的是板的抗折强度.由表2 可知：UHPC 棱柱体（400 mm×100 mm×100 mm）的抗折强度为24.8 MPa，基于单向板S1（900 mm×430 mm×60 mm）的极限承载能力，确定的UHPC抗折强度为25.6 MPa，二者相近，仅相差3.2%.

2.2.3 UHPC应变

单向板试件受力过程中跨中截面的应变分布如图12（a）所示.可见：直到峰值荷载，截面应变沿高度均接近线性分布，平截面假定较好地得到满足；截面受压区高度由开裂前的30 mm（50%板厚）降低到开裂后的约15 mm（25%板厚）后基本保持不变，反映了截面开裂至峰值荷载期间开裂截面受拉区钢纤维桥接作用的稳定发挥.

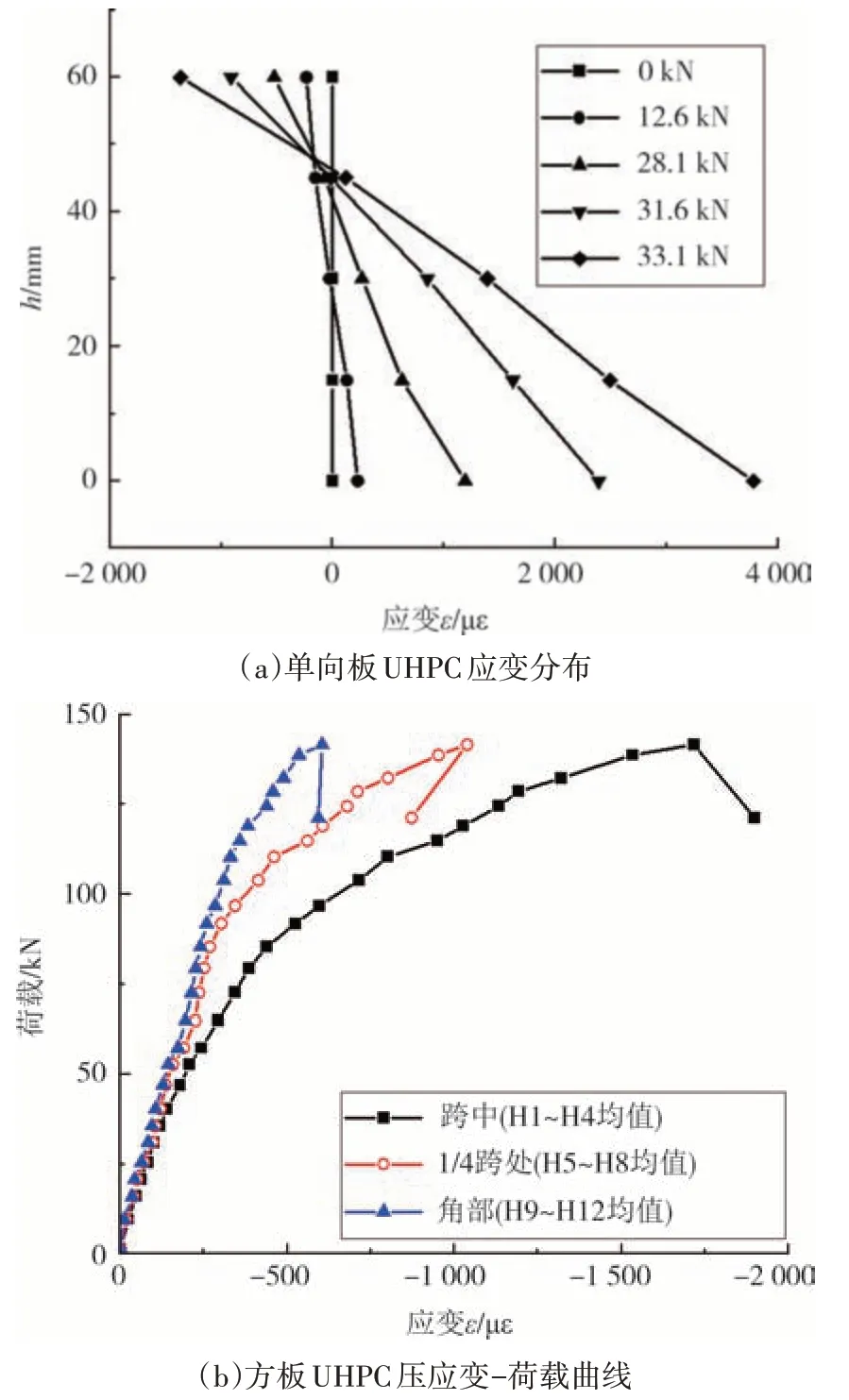
图12 UHPC应变曲线Fig.12 Strain curves of UHPC

方板试件受力过程中板顶面中心、1/4 跨以及角部对角线处的UHPC 应变变化如图12（b）所示.考虑结构和应变测点布置的对称性，且对称位置处应变测点压应变实测值亦较接近，为降低测点应变值的离散性，图中12（b）将相同区域对称布置应变测点的实测结果予以平均.H1～H4 为绕板中心对称布置在局部加载板周边的4 个应变测点，H5～H8 为绕板中心对称布置在板1/4 跨的4 个应变测点，H9～H12 为绕板中心对称布置在1/4 对角线长度位置处的4 个应变测点.可见：中心处的应变增长最快，1/4跨处应变次之，角部对角线处应变增长最慢.另从图12（b）中1/4板跨和角部1/4对角线长度处的应变发展比较可知：约65%峰值荷载以前，虽然角部对角线处的应变发展稍慢，但二者极为接近；其后1/4 板跨处的应变发展明显加快，使得板底主裂缝主要沿平行板边方向而非沿对角线方向发展，与图10 所示板底裂缝接近十字形的分布相对应，也与双向正交等强配筋钢筋混凝土方板极限状态时的主裂缝一般沿对角线发展的形态存在明显区别［43］.这主要是源于钢纤维在板平面内任一方向上的随机分布，使得无筋UHPC方板沿正交和对角线方向单宽截面上的抗弯承载能力基本一致，但板顶荷载主要沿路径较短的正交方向传递，因而板正交方向承受较大的单宽弯矩而更趋不利，使得破坏截面沿正交方向发展而接近十字形.文献［16］发生弯曲破坏的四边固支无筋UHPC方板试验中，也出现了类似的破坏形态.

峰值荷载时单向板板顶的压应变为1 337 με，方板板顶跨中、1/4 跨和角部等位置处的压应变分别为1 716 με、1 038 με 和604 με，均远未达到相应UHPC 的极限压应变（一般不小于4 500 με［42］），表明受压区的UHPC并未压碎，与试验现象吻合.

总之，无论是单向板还是方板，破坏均由临界截面受拉边缘附近区域UHPC 开裂、钢纤维受拉失效导致，而截面受压边缘的UHPC 均远小于其极限压应变而不可能被压碎，这里将这种破坏形态定义为受拉破坏.由于UHPC内钢纤维的增强作用，无筋UHPC板的抗弯承载能力和极限变形分别较相应的开裂荷载和开裂变形显著提高且表现出较好的延性破坏特征.

3 单向板截面的抗弯承载力

3.1 基本假定

计算无筋UHPC 单向板正截面抗弯承载力时，采用如下基本假定：

1）截面应变分布符合平截面假定.

2）因极限状态时，受压板边缘应变远小于UHPC的极限压应变，故UHPC 受压本构采用如图13 所示的线性关系，即为：

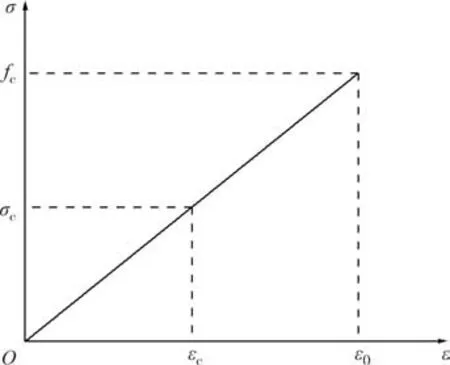
图13 UHPC受压本构关系Fig.13 Compressive constitutive model of UHPC

式中：σc为应变εc时的应力；fc为UHPC 的抗压强度，MPa；ε0为峰值应力fc对应的应变；Ec为UHPC的弹性模量，MPa.

3）不同钢纤维配置时UHPC 的轴拉本构关系分别采用如图6所示的双折线和三折线.

4）板在受拉边缘应变达到UHPC 的极限拉应变（εtu）时达到其极限状态，即板发生受拉破坏［44］.

3.2 数值分析方法及验证

图14 为极限状态下板截面的应变和应力分布，沿高度将截面划分为n层单元，截面的应变协调条件可表示为：

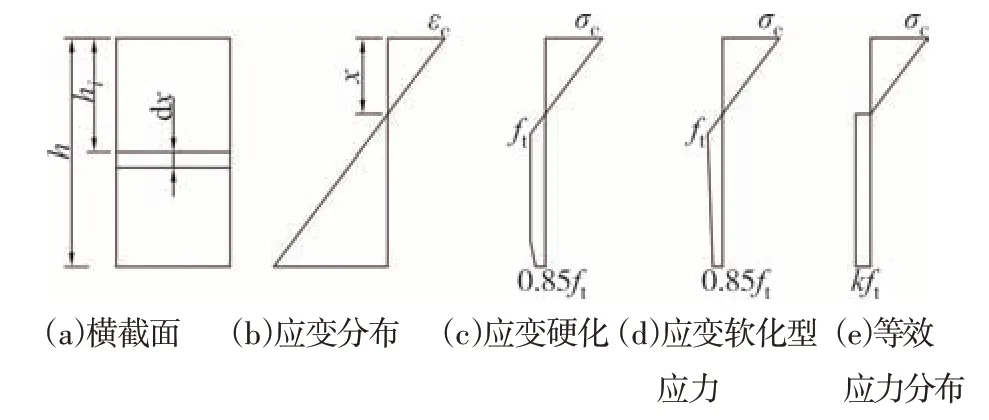
图14 极限状态下截面应变和应力分布Fig.14 Strain and stress distribution on the section at ultimate state

式中：φ为截面曲率；x表示受压区高度，mm；xo表示中性轴高度，mm；h表示截面高度，mm；hi为第i层单元重心距受压边缘的距离，mm；εci为高度hi处的UHPC 应变；εcf为受压边缘UHPC 的应变；σci和σti分别为第i层UHPC 单元的压应力和拉应力；bi为第i层单元的宽度.

图15为单向板S1跨中截面弯矩-曲率关系的计算和实测结果对比，其中截面的实测曲率系基于平截面假定依据图12（a）截面的实测应变确定.即基于板顶压应变和有效测点应变测值确定的受压区高度按式（7）近似计算截面应变分布的截面曲率.可见计算和实测结果吻合较好，验证了计算方法的适用性.

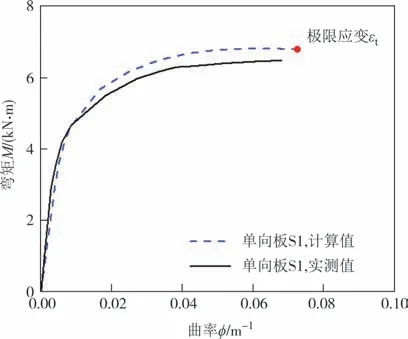
图15 单向板S1弯矩-曲率曲线Fig.15 Moment versus curvature curves of one-wayslab S1

3.3 纤维特征参数影响分析

不同纤维特征参数λf下截面的弯矩-曲率计算结果如表5 和图16 所示.定义截面的曲率延性系数为极限曲率φu（受拉边缘达到UHPC 极限拉应变时的曲率）与开裂曲率φcr之比.可见，随纤维特征参数λf的增大，截面的开裂弯矩Mcr、极限弯矩Mu和延性系数均相应提高.当纤维特征参数λf由0.65 分别增加到1.3、1.95和2.6时，开裂弯矩相应增加18%、34%和59%；极限弯矩相应增大39%、64%和98%；延性系数相应增大158%、283%和367%.这是UHPC的抗拉强度和极限拉应变均随着纤维特征参数的增大而提高所致.

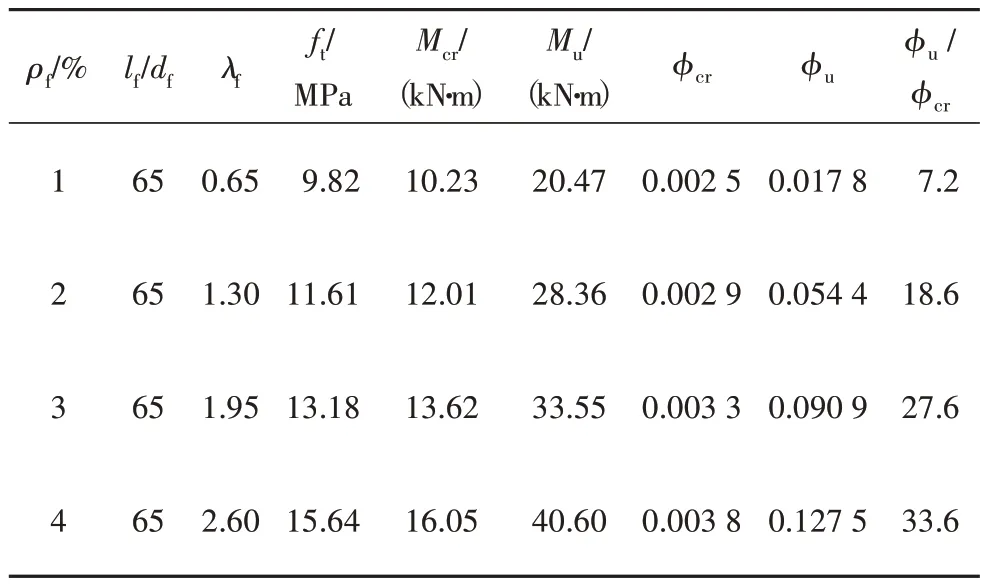
表5 不同纤维特征参数下板计算结果Tab.5 Calculation results of different λf

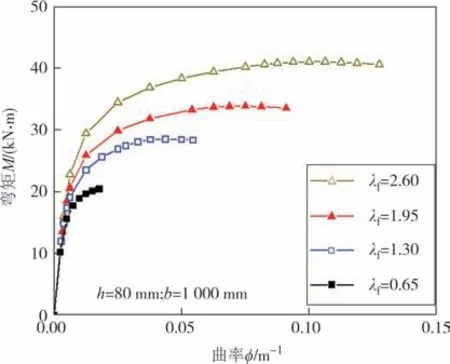
图16 不同纤维特征参数M-φ曲线Fig.16 M-φ curves under different λf

3.4 截面抗弯承载力简化计算

将受拉区UHPC 拉应力分布等效为矩形分布，相应的拉力T如式（10）所示.

系数k随纤维特征参数λf的变化规律如图17 所示.可见：系数k随纤维特征参数λf的增大而增大.λf由0.65 增加到2.6 时，k由0.84 增加到0.96.表明随钢纤维体积掺量和长径比的增大，极限状态时受拉区的应力分布更趋完全的塑性分布.对k进行曲线拟合可得到式（11）.

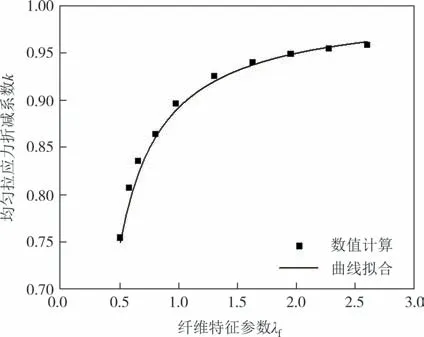
图17 k-λf 曲线Fig.17 k-λf curve

基于极限状态时截面的平衡条件和变形协调条件可得方程（12）～（14），并可据此确定截面的极限抗弯承载能力Mu.

式中：εcf为极限状态时受压边缘UHPC 的应变；εtu为UHPC的受拉极限应变，按式（3）确定.

对本文中S1 及国内外文献中22 块无筋UHPC单向板的抗弯承载能力进行了分析.这23 个试件（包含本文S1）的钢纤维体积掺量为1%～2%，板厚为40～60 mm，分析结果如表6所示.

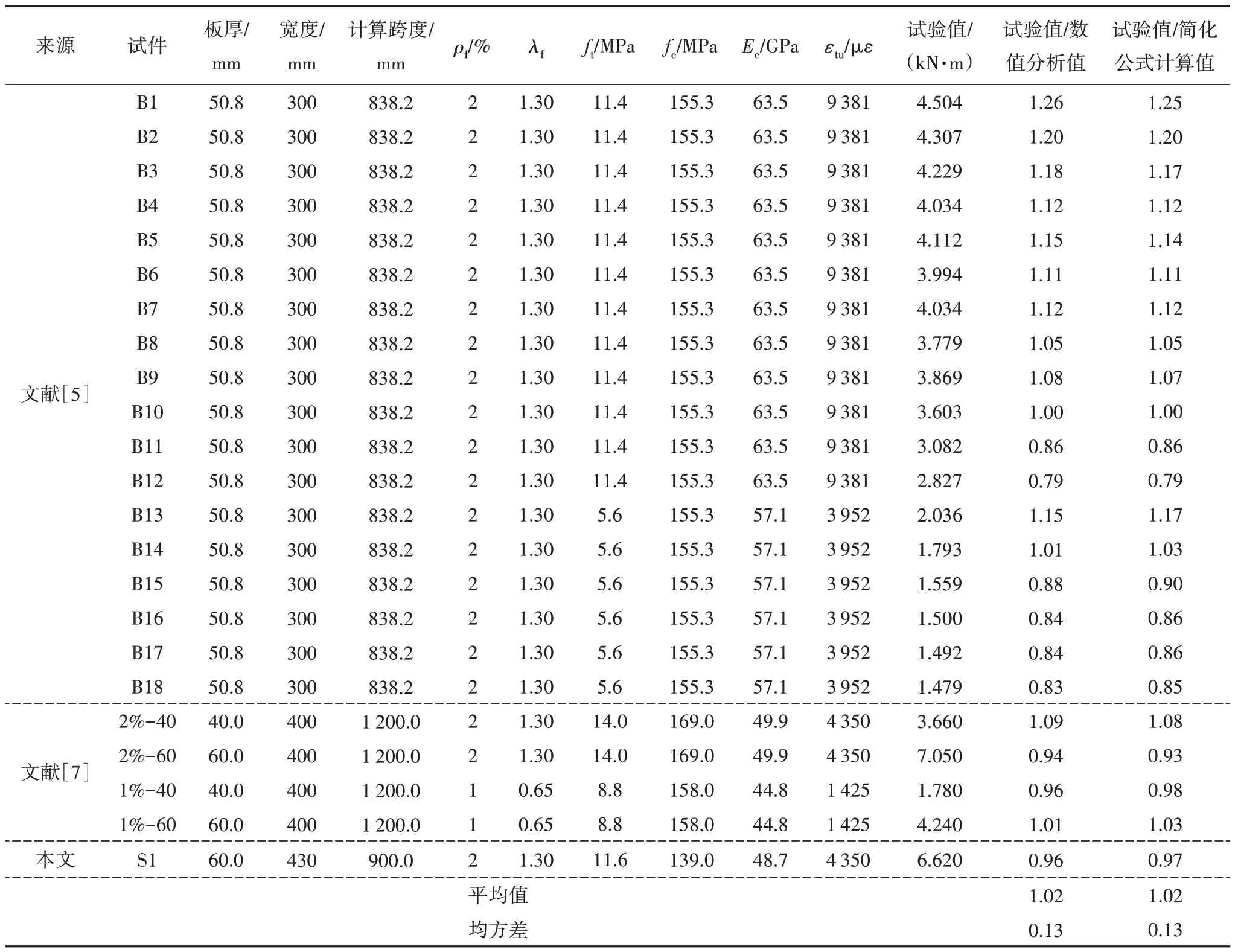
表6 UHPC单向板截面抗弯承载力试验值和计算值对比Tab.6 Comparison of experimental and calculated values for the flexural bearing capacity of UHPC one-way slabs

1）试验值与数值分析值及简化公式计算值之比的均值和均方差分别为1.02 和0.13 及1.02 和0.13.可见：简化分析方法和数值分析具有相近的精度，且均能较好地预测无筋UHPC板的抗弯承载力.

2）文献［5］中试件B1～B12 的UHPC 实测极限拉应变为9 381 με，B13～B18 的UHPC 实测极限拉应变为3 952 με，与式（3）计算得到的极限拉应变（4 350 με）相差较大.这源于试验中人为地控制了UHPC 基体内纤维取向，B1～B12中控制钢纤维沿纵向取向，能提高极限拉应变，而B13～B18中控制钢纤维沿横向取向，则会降低极限拉应变.而本文所提极限拉应变公式（3）是基于纤维分布近似于随机分布的试件，故实测值与计算值相差较大.当极限拉应变取为实测值时，B1～B12抗弯极限承载力试验的平均值约为计算值的1.07倍，B13～B18试验平均值约为计算值的94%.考虑纤维取向影响后计算值吻合较好.

4 方板的极限承载能力

4.1 塑性极限解

上述试验和数值分析结果均表明无筋UHPC 板截面和方板均表现出一定的塑性性能，故首先采用塑性极限分析方法来确定无筋UHPC 方板的极限承载能力，并分别采用机动法和静力法获得无筋UHPC方板极限荷载的上、下限解，以评价此时塑性极限分析方法的适用性.

参考板中部局部荷载作用下普通钢筋混凝土方板的塑性破坏机构［45］，对于无筋UHPC 方板，采用 图18所示的“X”形破坏模式确定相应的极限荷载.

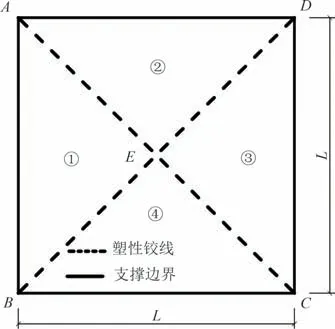
图18 方板破坏模式Fig.18 Failure mode of square slab

采用机动法分析时，取图18 塑性破坏机构的板块①为脱离体，其受力状态如图19所示［45］.根据脱离体的极限平衡条件可得无筋UHPC方板的极限荷载为：

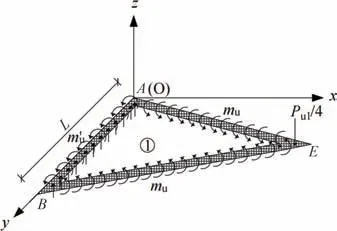
图19 机动法中板块①极限平衡状态图Fig.19 The limit equilibrium state of plate ①in kinematic method

采用静力法分析时，对于中部局部荷载作用下的方板，假定极限状态时连接板中和支座间任一板带内的弯矩均为图20 所示的线性分布且忽略截 面上的扭矩作用，则图示的弯矩分布同时满足平衡方程、边界条件和屈服准则［45］，并可确定此时无 筋UHPC方板的极限荷载为：

图20 静力法中板块①极限平衡状态图Fig.20 The limit equilibrium state of plate ①in static method

上述式中和图中：mu和分别为无筋UHPC 方板单宽截面上的正、负极限弯矩，均按式（12）～式（14）计算；四边简支时，取0.

采用式（15）和式（16）分别对文献［16］中发生弯曲破坏的四边固支无筋UHPC 方板和本文试验的简支无筋UHPC 方板S2 的极限承载力进行分析，计算结果和试验值列于表7.可见：基于机动法或塑性铰线法的式（15）计算值与试验值之比的均值和均方差分别为1.59 和0.19，计算值与试验值相差较大，表明塑性铰线法并不适用于预测无筋UHPC 方板的极限承载力，即受拉UHPC 的塑性尚不足以在无筋UHPC方板中形成完全的塑性铰线机构［16］；基于静力法的式（16）计算值与试验值之比的均值和均方差分别为0.79 和0.10，虽然静力法预测值偏小，但较机动法能更好地预测无筋UHPC方板的极限承载力.

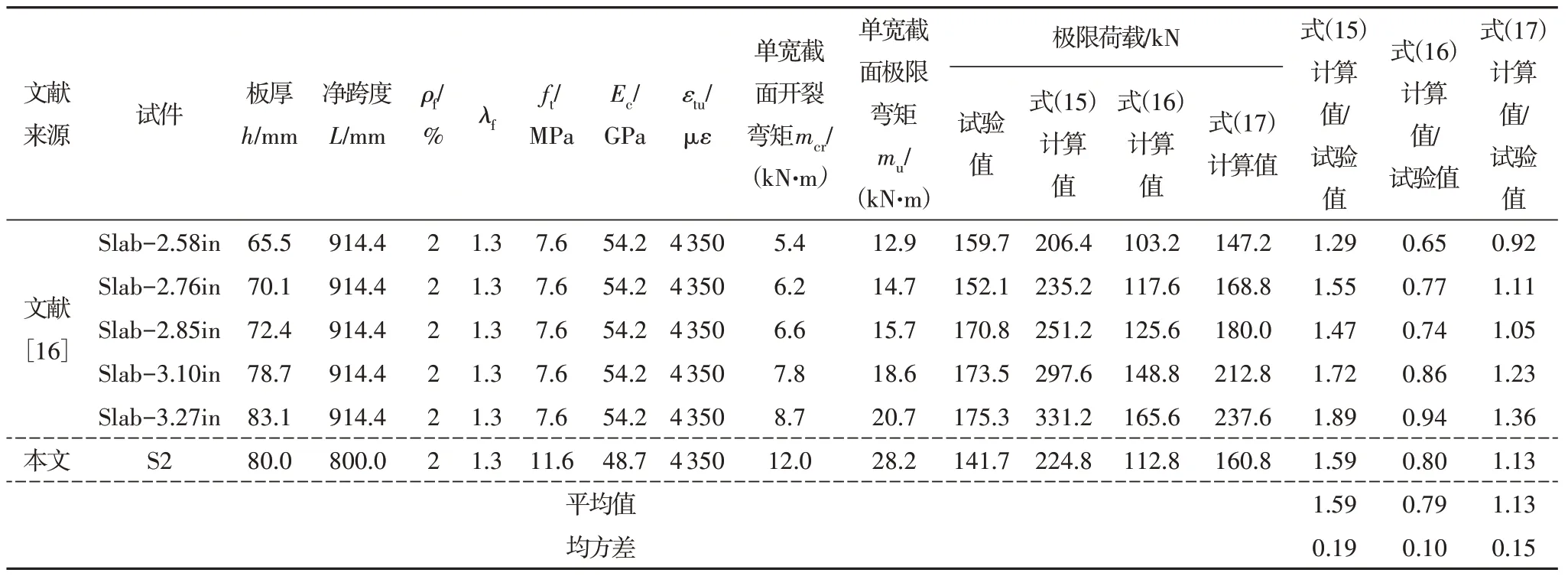
表7 方板的极限承载能力比较Tab.7 Comparison of ultimate bearing capacity of square slabs

4.2 近似分析解

前已述及，基于式（15）的塑性铰线解会过高地估计无筋UHPC 方板的极限承载力，表明极限状态时，沿图18 所示无筋UHPC 方板各破坏线上并非任一处截面上的弯矩均能达到极限弯矩.为此，假定板底正弯矩破坏线和板顶负弯矩破坏线上的弯矩均为如图21 所示的线性分布，且板底正弯矩由板中点处的截面极限弯矩mu线性变化至支座处的截面开裂弯矩mcr，板顶负弯矩由支座中心处的截面极限弯矩m'u线性变化至支座边缘处的截面开裂弯矩m'cr.则参照机动法，根据图21 所示脱离体①的受力状态，可确定板的极限承载力Pu3如式（17）所示.

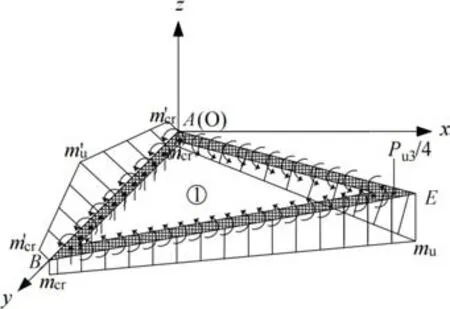
图21 近似分析法中板块①极限平衡状态图Fig.21 The limit equilibrium state of plate ①in approximate method

式中：mcr和分别为板单宽截面上的正、负开裂弯矩；mu和分别为板单宽截面上的正、负极限弯矩.四边简支时，和取0.

采用式（17）计算文献［16］中发生弯曲破坏的无筋UHPC 方板和本文试件S2 的极限承载力，结果亦列于表7.可见：式（17）计算值与试验值之比的均值和方差分别为1.13 和0.15，表明所提方法尚能较好地预测无筋UHPC方板的极限承载力.

值得注意的是，文献［16］中有不同板厚但仍发生弯曲破坏的无筋UHPC 试验方板，随着板厚增加，塑性绞线法对板的极限承载力高估更多，表明板厚越大，板的延性越差，完全的塑性铰线机构越难形成，即无筋UHPC 方板的极限承载能力存在明显的尺寸效应，这一点无疑值得进一步研究.

5 结论

基于国内外无筋UHPC 单向板和方板受弯破坏性能的试验结果及本文的试验研究和理论分析，可得出以下结论：

1）虽然无筋UHPC 单向板和方板均发生由UHPC 抗拉性能所控制的受拉破坏，但由于UHPC 内钢纤维的增强作用，无筋UHPC 板的抗弯承载能力和极限变形分别较相应的开裂荷载和开裂变形显著提高且表现出一定的延性破坏特征；周边支承超静定方板内存在的弯矩重分布过程，使无筋UHPC 方板的延性性能有所增强，但受拉UHPC 的塑性尚不足以保证板中完全塑性铰线机构的形成.因此，塑性绞线法并不适用于预测无筋UHPC 方板的极限承载能力，而静力法却能给出相对较好且偏于安全的预测结果.

2）基于本文及文献的试验结果，考虑钢纤维特征参数的影响，提出了UHPC 材料的受拉本构和无筋UHPC 板截面受拉区等效均布应力折减系数k的计算公式，建立了无筋UHPC 单向板截面抗弯承载能力的简化计算方法，并以试验结果验证了方法的适用性.

3）假定极限状态时沿板破坏线上的弯矩近似呈线性分布，提出了周边支承无筋UHPC 方板极限承载力的近似估计方法，试验结果表明所提方法尚能较好地预测无筋UHPC方板的极限承载力.

文献［16］的试验结果表明，周边支承无筋UHPC方板的极限承载能力存在明显的尺寸效应，这一点值得进一步研究.