基于块体体积和岩体波速的岩体力学参数估算方法

刘婷婷，李闯闯，黄文旭，李新平，2，郭运华，2

（1.武汉理工大学 土木工程与建筑学院，湖北 武汉 430070；2.武汉理工大学 三亚科教创新园，海南 三亚 572024）

由于岩体力学参数在岩体工程的设计、分析中占据着重要地位，加之不同地理环境、不同地质条件、不同工况等使得岩体力学参数复杂多变，因此如何获得可靠的岩体力学参数一直是广大岩体力学工作者面临的难题之一.

如何在易操作、简便快捷的原则上，提出一种可以满足工程需要的岩体力学参数估算方法，已成为近年来人们关注的目标和趋势.由于较全面地考虑了岩体的结构特征对岩体强度的影响，Hoek-Brown准则更符合工程实际，也是发展最为完善的方法，使用该准则的关键是确定地质强度指标GSI 和岩体扰动参数D，但其创立者Hoek 仅给出了GSI 的概化取值［1-3］和D值的概化取值区间［4］，无法使其定量化，造成取值主观性强、误差大，无法满足工程实际需要的问题.随后，一些学者对此进行了研究并取得了相应成果.例如，Sonmez 和Ulusay［5］为了改善参数计算精度，引入开挖影响系数df，但准确获得df值较困难；苏永华等［6］针对GSI 量化困难问题，将可量化参数RMR 分类值、岩体块度指数、风化指标引入，使该问题得以解决；闫长斌和徐国元［7］虽然给出了计算D的具体方法，但缺点在于RMR 值仍需要量化；夏开宗等［8］提出以岩体波速Vp计算Hoek-Brown 准则参数，虽然给出了实用的具体量化方法，但缺点在于对扰动岩体的适用性较差；李硕标及薛亚东［9］在岩体波速法的基础上提出的改进计算方法，也不适用于质量差的岩体.

针对上述Hoek-Brown 强度准则参数量化问题，结合学者们对传统Hoek-Brown 准则的改进成果，提出Hoek-Brown 准则参数的量化方法，采用块体体积Vb（节理密度的体积表达式）计算地质强度指标GSI及采用岩体纵波波速Vp计算岩体扰动参数D，进而求取岩体力学参数.同时采用数值模拟软件FLAC3D对所获取的力学参数进行反演计算，结合田西高速项目黄果峰隧道实测数据对比分析，验证其工程应用效果.

1 Hoek-Brown准则

Hoek 和Brown［10］在基于Griffith 强度理论的基础上提出了狭义的Hoek-Brown 强度破坏准则，后续又针对该准则的不足，提出了修正后的经验公式：

式中：σ1、σ3分别为岩体破坏时的最大和最小主应力；σc为岩块单轴抗压强度，MPa；mb、s及a均为岩体的材料参数，与其岩性和结构面状况有关，且均可表示为地质强度指标GSI和岩体扰动参数D的函数：

式中：mi为完整岩块的Hoek-Brown 准则常数，其值反映岩石的软硬程度；GSI 与岩体结构、岩体中岩块的嵌锁状态及结构面表面特征有关.

2 基于块体体积和岩体波速的岩体力学参数估算方法

2.1 块体体积Vb计算方法

块体体积是由节理间距、节理方位、节理组数以及节理连通性决定的，是衡量岩体质量的重要指标.块体体积是节理密度的体积表达式.当岩体存在3个或3 个以上节理组数且节理贯通的情况下，如图1所示，其体积可计算［11］为：

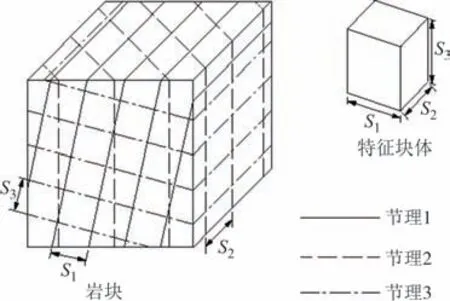
图1 含3组节理的块体示意图Fig.1 Block diagram containing 3 joint sets

式中：S1、S2及S3分别表示同一节理集相邻节理的间距，m；γ1、γ2及γ3为节理集之间的夹角，°.但与节理间距变化相比，节理集交角的影响相对较小.因此，块体积可以近似为：

2.2 地质强度指标GSI计算方法

基于大尺度节理剪切试验和数据反分析，Palmstrom［12］给出了用于定量描述块体体积大小、节理表面特征和延展度的特征参数Jp的计算公式：

式中：Jc为节理条件因子，K为与Jc相关的参数，可由式（6）计算［12］：

Jc的取值与节理尺寸和连续性系数（JL）、粗糙度系数（JR）和蚀变系数（JA）等三个参数有关，可由下式计算：

基于大量的数据回归分析，意大利学者Russo［13］建立了基于特征参数JP的地质强度指标GSI 定量计算公式：

将式（5）～式（7）带入式（8），可得地质强度指标GSI与块体体积Vb的定量关系：

2.3 岩体扰动参数D的计算方法

根据岩体波速，可计算得到岩体扰动参数D［12］为

式中：Vp和Vup分别是扰动后岩体波速和未扰动岩体波速，m/s.

将式（9）和等（10）带入公式（2），可得Hoek-Brown 常数mb、s、a与块体体积（Vb）和岩体波速（Vp）的定量关系.

结合本文所给出的计算公式（9），代入式（2）可得到mb，s，a值：

2.4 岩体力学参数估算

2.4.1 岩体变形模量Em的计算

岩体单轴抗压强度σc和岩体单轴抗拉强度σt的计算可参照文献［8］，此处给出岩体变形模量的计算方法：

2.4.2 岩体抗剪强度

根据Hoek 等［4］的研究表明，对于Hoek-Brown 准则，与之等效的岩体抗剪强度参数内摩擦角φ和黏聚力c的计算公式为：

其中：

σ3max为最小主应力上限值，对于岩石边坡和隧道工程σ3max取值为：

式中：σcm为岩体抗压强度，MPa；γ为岩体重度，kN/m3；Ht为隧道埋深，m；Hs为边坡坡高，m；当σt＜σ3＜σc/4时，有：

将式（11）～式（13）计算结果带入式（15）和式（16）中即可得到基于块体体积计算的岩体抗剪强度参数.

2.5 地质强度指标GSI计算值对比

许多学者就如何量化地质强度指标GSI 值进行大量研究，如Russo［13］和Cai［11］提出了基于块体体积并考虑节理结构面条件的GSI值计算方法，在GSI系统中，节理结构面条件由结构面粗糙度、风化条件和填充条件决定，这些因素的结合表征了节理块体的强度，采用节理条件因子（Jc）来量化.

结合Winn 等［14］的文献数据，将本文计算GSI 方法与Russo法、Cai法作对比，计算结果如表1所示

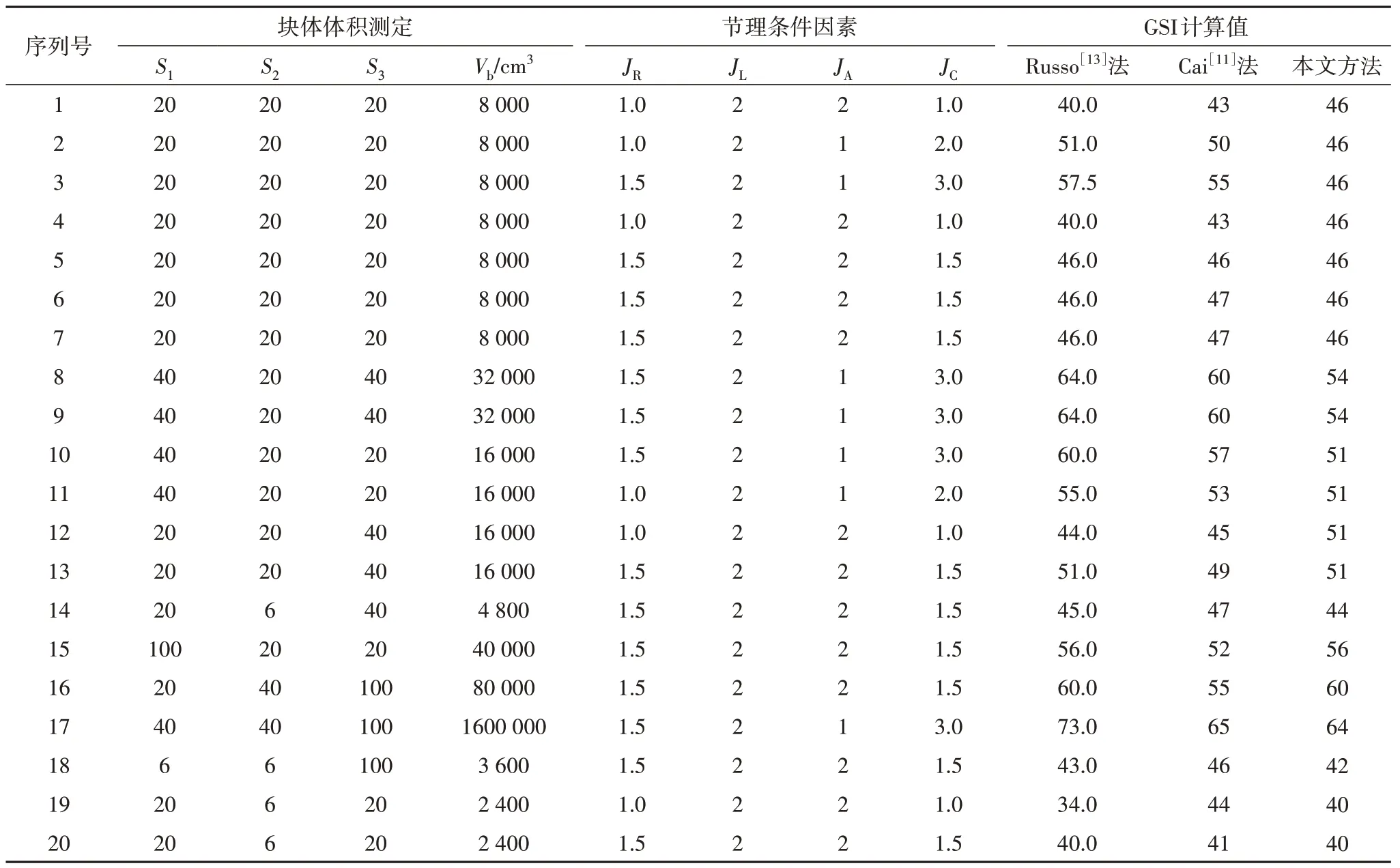
表1 3种方法计算GSI值比较Tab.1 GSI values calculated by three methods

本文所给出的计算GSI 的方法取决于块体体积的测定，其值的获取较为简便，且量化程度高、人为因素误差小，计算结果稳定.从表1可以看出，本文计算GSI所得值与Russo［13］法、Cai［11］法计算值的平均相对误差分别为3.4%、2.4%，说明基本与Russo［13］法和Cai［11］法所给出的GSI 值等效，由此可见采用块体体积来计算GSI 值，不仅所需考虑变量少，还更易应用于工程实际，而且计算结果的准确性也能得到保证.

3 工程实例验证

3.1 工程背景

拟建田西至西林（滇桂界）高速公路K183+565黄果峰隧道位于西林县马蚌村西北侧山体，隧道地区属构造剥蚀、侵蚀中低山地貌，山体连绵起伏，地形地貌主要受地层岩性及地质构造控制，山脉走向多呈北西-南东向，与构造线走向基本一致，与隧道走向大致斜交.拟建隧道分左、右线，左线起止桩号：ZK183+574～ZK185+590，设计长度为 2 016 m，进、出口路基设计高程分别为943.632 m、925.541 m，最大埋深约225 m（ZK184+720 处）；右线起止桩号：K183+572～K185+555，设计长度为 1 983 m，进、出口路基设计高程分别为943.621 m、926.241 m，最大埋深230 m（K184+660处）.

3.1.1 岩体波速测取

为使研究具有代表性、适用性，选取隧道入口段、中段、出口段以及左、右线共计六个掌子面进行分析.根据现场超前地质预报（图2）对相邻掌子面原岩波速结果进行分析，为了确定开挖爆破对岩体的扰动范围和未扰动范围，通过计算相邻掌子面的岩体波速变化率ƞ，以ƞ=10%为界限，其中较小的区间为爆破开挖扰动范围，较大的区间为原岩波速［15］，如表2所示.

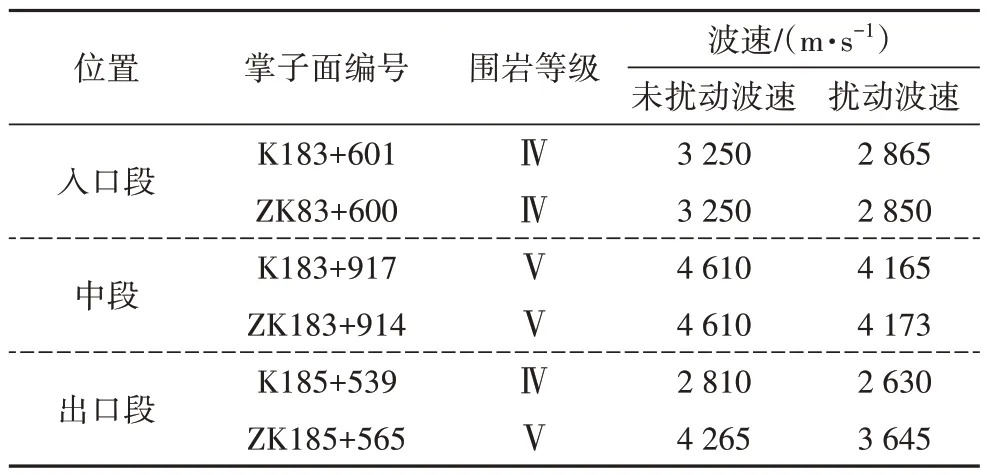
表2 岩体波速平均值Tab.2 Average ultrasonic velocity values of rock mass

图2 现场波速测取Fig.2 Field ultrasonic velocity measurement

3.1.2 节理分布统计

此处对隧道中段进行举例说明，根据该区域地质资料并结合地质调勘成果，发现隧址区穿过三叠系中统兰木组（T2Ⅰ）地层，表面受风化、构造等影响，节理裂隙发育.现场节理裂隙分布图如图3～5 所示，其下伏基岩为砂岩，局部夹杂泥岩，多以中厚—厚层状构造为主，裂隙多以风化裂隙为主.在隧址附近测得三组节理，产状分别为第一组（J1）：150° ∠68°（2～4 条/m）取S1=0.33 m；第二组（J2）：70°∠25°（3～5条/m）取S2=0.25 m；第三组（J3）：240°∠32°（5条/m）取S3=0.5 m，统计结果如表3所示.

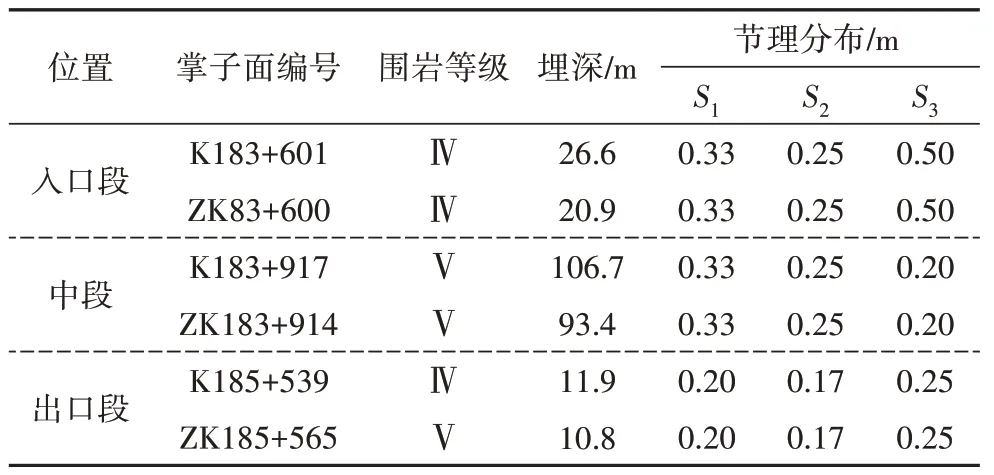
表3 节理分布统计Tab.3 Statistics of Joint sets

图3 节理产状J1Fig.3 Joint sets J1

图4 节理产状J2Fig.4 Joint sets J2

图5 节理产状J3Fig.5 Joint sets J3

3.1.3 围岩物理参数

根据设计资料结合现场原位测试及室内试验成果，对隧址区内各岩土层的物理力学性质按有关规范进行统计，如表4所示.

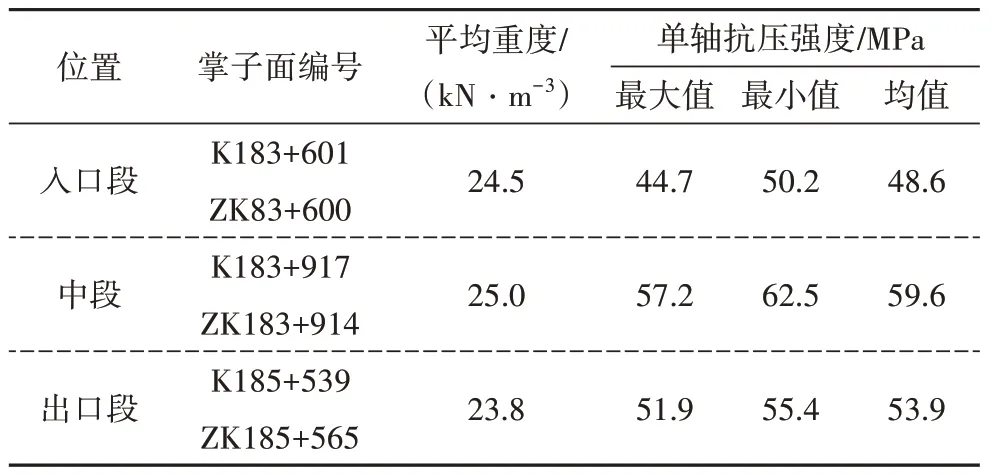
表4 室内岩石物理力学参数Tab.4 Physical-mechanical parameters of rocks from laboratory tests

3.1.4 岩体评价值及Hoek-Brown参数

将表4 中数据代入式（4）可得Vb值，而后代入式（11）～式（13）即可求得GSI 值；将表3 中数据代入式（14）得到扰动参数D值，结合表5各掌子面室内岩石试验成果，将以上计算所得代入式（15）求得Hoek-Brown常数，如表5所示.

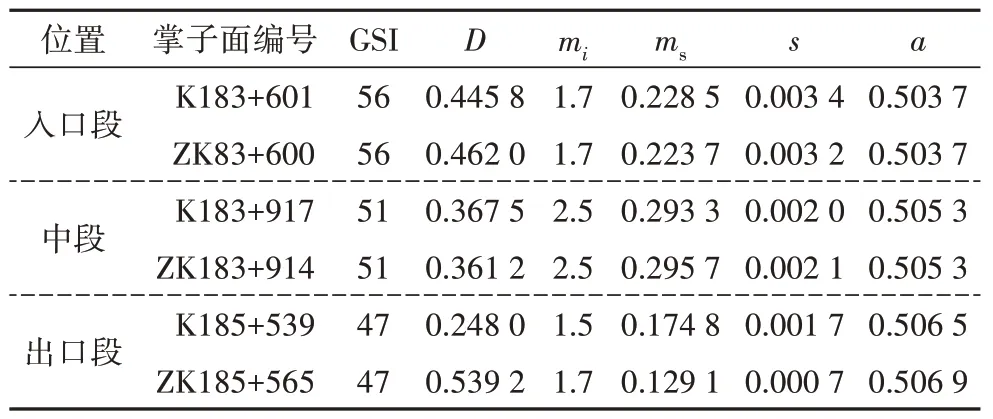
表5 岩体评价值及Hoek-Brown参数Tab.5 Evaluation result of rock mass and Hoek-Brown constants

3.1.5 岩体力学参数估算

由表5 所列出的Hoek-Brown 参数mb、s、a以及表3 所给出的室内岩石物理力学参数，代入式（14）～式（16）中计算得出岩体力学参数.如表6所示.

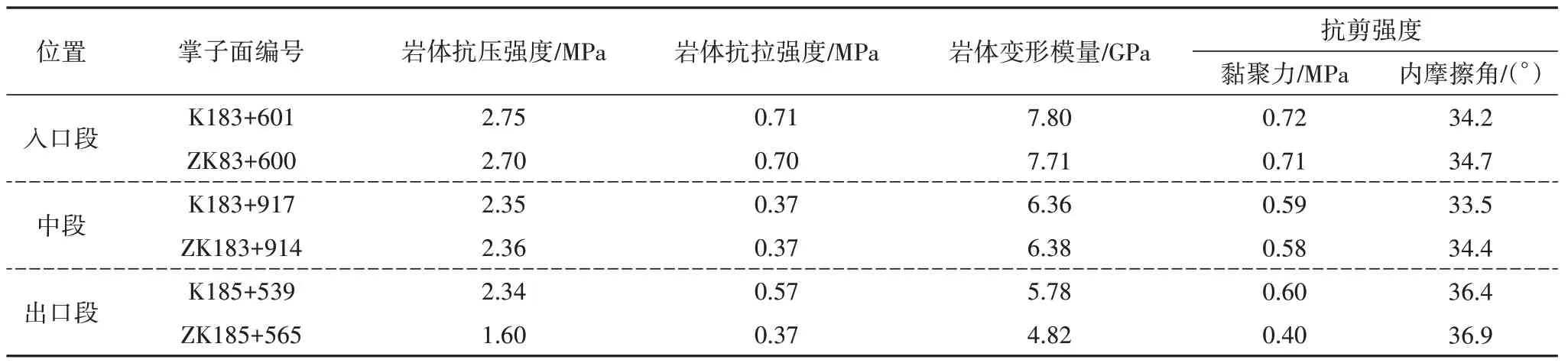
表6 岩体力学参数估算值Tab.6 Estimated value of rock mass mechanical parameters

3.2 基于FLAC3D数值模拟的预测参数评估

使用FLAC3D数值模拟软件对拟建隧道进行建模，取表6 隧道中各掌子面数据导入其中，设置垂直和水平测点，测点布设如图6 所示，模拟拱顶下沉和水平收敛，将模拟结果与实测值对比分析.依据隧道建筑限界拟定隧道断面内轮廓为单心圆曲边墙形式，隧道的中心垂直剖面为其对称面，可对一半隧道进行建模，隧道长40 m，净宽11.1 m，净高8.85 m，其中仰拱开挖深度为3.3 m；采用台阶法开挖，以喷射混凝土、钢筋网片、钢拱架作为衬砌支护，衬砌厚度为0.2 m，初始应力取决于重力荷载，水平应力与垂直应力关系为σzz=σxx=2σyy，建立模型如图7所示

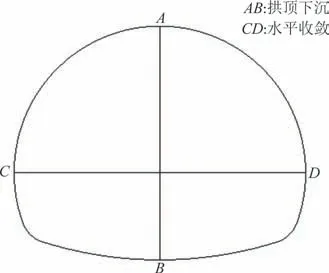
图6 测点布设示意图Fig.6 Equipment layout sketch of measuring points

3.3 现场监测工作

水平收敛及拱顶下沉的监测工作，在每次开挖后尽早进行，最迟不大于12 h，并且应在下一循环开挖前完成.现场监测工作如图8 所示，该隧道采用台阶法开挖，在拱腰处设置一条测线，采用激光测距仪监测水平收敛，拱顶下沉主要在拱顶中央布设了一个测点，为了防止在施工过程中的破坏，在拱顶两侧各补充了备份测点，采用高精度水准仪监测.检测周期：掌子面建成后2 次/d 持续7～10 d，此后1 次/d 直至累计变形值收敛且稳定5 d以上，监测终止.

图8 现场监测情况Fig.8 Scenarios of field test

将现场实测值与模拟值监测曲线列举如下：

1）隧道入口段，见图9～图10；

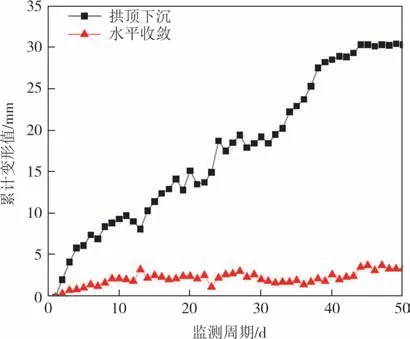
图9 K183+601实测曲线图Fig.9 Field measurement of K183+601

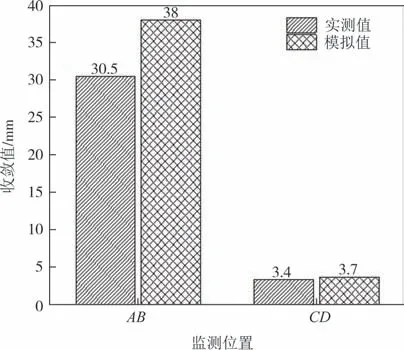
图10 K183+601实测模拟比对图Fig.10 Comparison between field measurement and model test results of K183+601

2）隧道中段，见图11～图12；

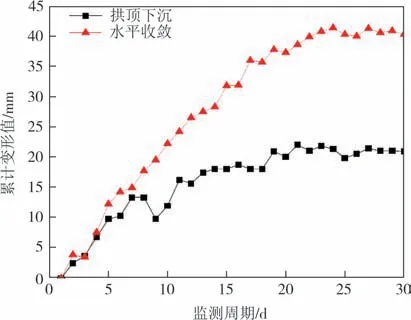
图11 K183+917实测曲线图Fig.11 Field measurement of K183+917

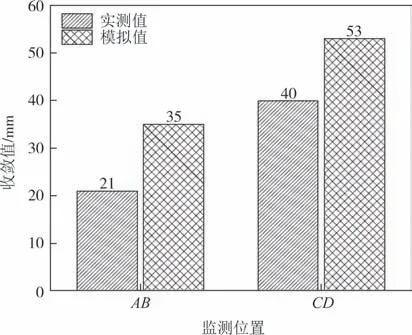
图12 K183+917实测模拟比对图Fig.12 Comparison between field measurement and model test results of K183+917

3）隧道出口段，见图13～图14.

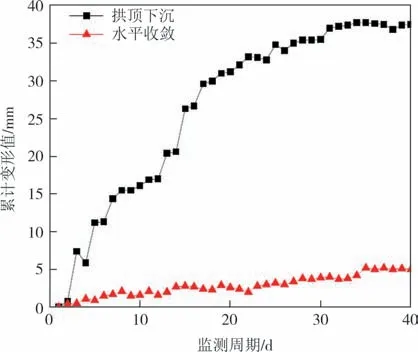
图13 K185+565实测曲线图Fig.13 Field measurement of K185+565

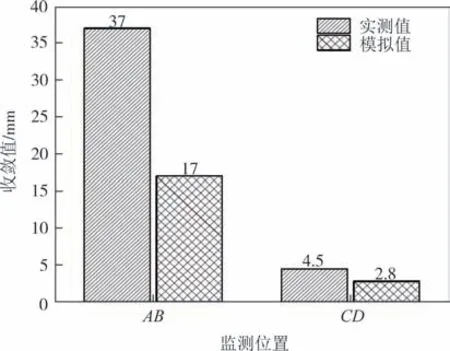
图14 K185+565实测模拟比对图Fig.14 Comparison between field measurement and model test results of K185+565

3.4 对比结果分析

图10、图12、图14分别列出了隧道入口段、中段及出口段各掌子面的拱顶下沉、水平收敛的累计变形实测值与模拟值，通过对比可知，实测拱顶下沉值与模拟值最大相差20 mm，最小仅为 3 mm，实测水平收敛值与模拟值最大相差13 mm，最小仅为1.6 mm，均在误差范围内.由此可见，估算的岩体力学参数基本符合现场实际情况，说明本文方法是可行的.

图9、图11、图13分别列出了隧道入口段、中段、出口段各掌子面的拱顶下沉、水平收敛实测曲线，通过对比分析可知，各掌子面的剧烈变形阶段均出现在掌子面开挖后的7～10 d内，说明隧道开挖后，改变了原有的应力环境使得内部应力释放而产生较大变形，而后在衬砌及支护的作用下又逐渐恢复平稳达到新的内力平衡，故而最终变形均收敛在一个定值范围内.此外，分别位于隧道入口及出口处的K183+601、K185+917 掌子面的拱顶下沉及水平收敛的累计变形值均较小，这是由于隧道出入口处埋深较小，内部应力主要为垂直方向上的地应力，水平方向的构造应力几乎不产生影响，所以拱顶下沉与水平收敛累计变形值小.但对于隧道中段的K183+917 掌子面，埋深达到106.7 m，此时其内部的应力环境复杂，垂直方向上的地应力较高但构造应力作用更加凸显，因此水平向的变形速率大于拱顶下沉，并且最终水平收敛的累计变形值也大于拱顶下沉.

3.5 数值模拟分析

根据上述估算所得力学参数，对隧道开挖过程采用FLAC3D法进行稳定性分析.如图15 所示，为新进开挖掌子面塑性区分布图.其中，“Liner”表示衬砌，“None”表示未发生屈服，“shear”表示剪切屈服，“tension”表示拉伸屈服，“n”表示当前屈服，“p”表示过去屈服.

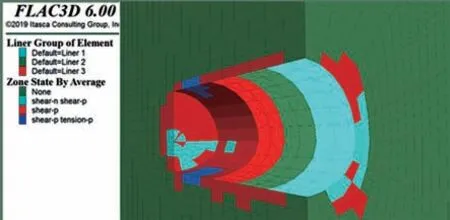
图15 掌子面塑性区Fig.15 Plastic zone of tunnel face

图15模拟的是掌子面K185+565的开挖工况，从图15 中可以看出在开挖后在掌子面以及拱腰处出现了一定区域的拉伸和剪切破坏区，特别在仰拱开挖界面出现了临塑状态.结合现场调查发现，此处虽已经支护完毕，但仍出现了喷浆混凝土脱落、钢拱架变形的迹象，现场状况如图16～图18 所示.结果表明：数值模拟结果与现场情况吻合，印证了估算所得岩体力学参数的适用性.

4 结论

以Hoek-Brown 准则为理论依据，建立了基于块体体积和岩体波速的岩体力学参数估算方法，结论如下：

1）以节理条件因子Jc来确定结构面特征参数Jp与块体体积Vb之间数量关系，并以Jp为中间变量建立基于块体体积Vb计算地质强度指标GSI 值的方法，其计算结果与已有方法计算值较为一致，验证了基于Vb计算GSI值的可行性.

2）采用基于块体体积Vb和岩体波速Vp的岩体力学参数估算方法获取的岩体力学参数对隧道的开挖过程进行模拟，其计算结果与现场实测数据基本吻合，进而验证了其工程效果的合理性.

3）块体体积计算方法既适用于规则节理，也适用于不规则节理.当节理分布不规则，或是现场存在多个节理组时，可以选择有代表性的块体，即可直接测量块体体积.此外，在计算地质强度指标GSI 时，文中方法可以克服岩体波速法仅适用于岩体波速大于1 700 m/s 的情况，对于质地较差的岩体也同样适用，因此其应用范围更广.