海洋场地Rayleigh 波传播特性及其影响因素分析

肖萌，崔杰，李亚东†，江杰，单毅，Duhee Park

（1.广州大学 土木工程学院，广东 广州 510006；2.广东水利电力职业技术学院 市政工程学院，广东 广州 510000；3.广西大学 土木工程学院，广西 南宁 530004；4.汉阳大学 环境与土木工程学院，韩国 首尔 04763）

地球是一种复杂的层状多相介质，包含了空气、水、土壤和岩石层等，自然场地的复杂性和地震波自身的不确定性让地震波的传播特性和对土体的动力响应影响特性研究进展缓慢.特别是在海洋环境中，海水和土层两种不同介质运动状态的不同，以及相互之间的影响和接触，导致地震传播界面和传播介质的性质对地震波的传播有很大影响，因此，地震波在饱水地层中传播的研究也曾引起了广泛关注［1-3］.1976 年唐山大地震、1995 年日本阪神大地震、2008年汶川大地震、2017 年墨西哥地震等这些危害极大的地震均为浅源地震.对浅源地震而言，体波在距离震中较远的地区已经衰减得很弱了，此时地震面波起主要作用，其中Rayleigh 面波传播远、振幅大、影响大，易引起土体液化.像唐山大地震这类震级高、危害大的地震，都离不开Rayleigh 波的影响.然而，针对海洋工程结构的破坏目前还鲜有案例.也因此，建立完善的海洋场地地震动力模型对地震波及其影响研究尤为重要.

Biot［4-5］提出的弹性波在饱和多孔介质中的低频和高频传播行为的扩展理论，反映了固液两相耦合的特性，目前已成为声学、地球物理等领域的标准参考以及后续研究的基础.许多学者如Deresiewicz等［6-7］、Berryman［8］也对多孔介质中波的传播进行了理论研究.在Biot 理论的基础上，Zienkiewicz 等［9-10］讨论了饱和多孔介质动力学行为的数值方法，特别是描述饱和岩土材料力学行为的数值方法.黄江等［11］通过饱和多孔介质动力学方程，对Rayleigh 波在两相介质中的传播以及一维土层的动力反应问题进行了分析，研究了惯性力与不同荷载类型对饱水土体动力反应的影响.Liu 等［12］研究了频域下Rayleigh波和Love波在由微观不可压缩线性弹性固体骨架组成的饱和多孔介质中的衰减和传播特征，其中孔隙液体视为不可压缩.陈炜昀等［13］在Chen 等［14］不渗透边界的基础上对非饱和土中Rayleigh 波的频散方程进行了推导，讨论了透水和不透水边界条件下土体的饱和度对Rayleigh 波传播速度与衰减的影响.Li 等［15］针对渗透系数极端条件下的线弹性各向同性饱和孔隙介质的瞬态动力分析问题，提出了一种u-U形式的时域黏弹性簧传输边界.但以上研究主要针对的是土体的饱和度、边界条件或是渗透系数极端条件下的研究分析，对于弹性模量、孔隙率、渗透系数的变化对Rayleigh 波的影响情况并未进行详细深入讨论，也没有涉及Rayleigh 波对土体参数的动力响应影响.

国外学者多用物理方法研究Rayleigh 波在饱和多孔介质中的传播，而Rayleigh 波的衰减和传播特性常被放在多孔弹性半空间中讨论.Kumar 等［16］研究了非均质和均质两层液体下饱和不可压缩多孔半空间中Rayleigh 表面波的传播.Kumari 等［17］对饱和多孔半空间中Rayleigh 波在不规则界面的传播和衰减特性进行研究，讨论了孔隙的微极性和水土的相互影响.Mahmoodian 等［18］在Biot 理论框架下，对Rayleigh 波、Love 波和Stoneley 波在横观各向同性饱和弹性半空间中的传播特性进行了对比分析，研究了多孔介质的力学参数（如孔隙率、地震波频率、渗透性等）对弹性波传播的影响，从物理角度解释了波速和相应衰减系数对材料参数的依赖性.Dao 等［19］从理论角度讨论了弹性半空间条件下，正交各向异性介质中时谐载荷作用下的Rayleigh 波的传播.通过公式推导，对弹性半空间正交各向异性表面波的运动进行了精确的解析预测，讨论了载荷类型对所产生的波场位移幅值的影响.Asano［20］和Vashisth等［21］研究了弹性波在波纹界面上的反射和折射.以上研究仅涉及传播介质的微观孔隙性质、传播界面，或荷载类型对Rayleigh 波传播的影响，同样并未考虑Rayleigh波对介质力学参数的影响.

为研究Rayleigh 波在复杂海洋场地的传播特性及其对海床土力学参数的动力响应影响，本文建立了Rayleigh 波在海洋场地传播的数学模型，并对无上覆海水、水-土界面平整有上覆海水、水-土界面不平整且有上覆海水这3 种不同场地条件的模型进行分析.建立了海洋场地饱和两相介质动力学方程，考虑了传播界面、土体的剪缩和剪胀的体变等本构特性，以及海水渗流的影响.通过公式推导得到不同情况下的Rayleigh 波方程，分析了不同场地条件下Rayleigh 波的传播和衰减情况，研究了孔隙率、渗透系数、弹性模量等参数对Rayleigh 波相速度和衰减的影响，并讨论了孔隙率、渗透系数等土体力学参数与Rayleigh 波波速对土体位移、应力、孔压等参数的动力响应影响，旨在为海洋工程抗震设防提供参考.

1 模型的建立

为讨论Rayleigh 波在上覆海水的不规则海底中的传播特性及对土层的影响，本文建立了Rayleigh波在饱和多孔弹性半空间中传播的数学模型.由于Rayleigh波在固液两相介质中传播会发生衰减，故取其波数k的复数形式为：

同样地，式（2）中表示的地震波波速的实部也是实际波速，虚部表示波速的衰减，w为地震波角频率.

图1 所示为所建立的坐标系和简化模型，考虑了有限厚度H的液体层覆盖在有褶皱界面的饱和多孔半空间上，其中：g（x）为海水层与土体之间的不规则界面的函数，g（x）≤z≤ ∞；g（x）是x的连续函数.在坐标系中，x轴和y轴是两个垂直的水平坐标，z轴垂直向下.地震波波前垂直于y-z平面入射，并在x-z平面上传播，因此，只讨论x-z平面上的波的二维传播问题.

图1 模型的建立Fig.1 Establishment of model

以O为原点，根据Asano［20］的研究，褶皱界面的傅里叶级数为：

式中：gn和g-n是傅里叶级数展开的系数，n是级数展开的阶数；，dn和sn分别是cos 和sin 傅里叶系数.本文采用的界面函数表示为g(x)=d⋅cospx，其褶皱的波长是 2π/p.在后续有褶皱界面的计算中，两个褶皱参数d的取值为1，p取π/2.设（U1，U2，U3）为两相介质的位移，（u1，u2，u3）和（v1，v2，v3）分别为半空间多孔介质固相和液相的位移分量，均为与时间t有关的函数.关于Rayleigh 波在x方向上的传播，有：u1=u1（x，z，t），u3=u3（x，z，t），v1=v1（x，z，t），v3=v3（x，z，t），U1=u1（x，z，t），U3=u3（x，z，t），

2 运动方程

2.1 上覆海水的欧拉方程

对于上覆海水的液体层，给出了运动方程和应力分量：

其中：（U1，U2，U3）是沿（x，y，z）方向的位移分量；λ1是液态层弹性常数（体积弹性模量）；ρ0是密度；σij是应力分量.把位移分量U1、U3和流体压力p1用位移势函数ψ表示，可得：

式中：A1和A2是任意常数；k是波数；c/β0是无量纲的相速度.

2.2 两相介质的运动方程与本构关系

Rayleigh 波在饱和两相介质中传播的运动学方程由以下微分方程表示［22-23］：

利用式（10）和式（11）中给出的本构关系和传播特性，推导得到：

为了求解方程（12），引入标量势函数φ1、φ2和矢量势函数φ1、φ2的Helmholtz表示：

由于仅讨论二维平面波（xoz平面）的传播问题，因此，uy=vy=0，可得到以下公式：

引入势函数后整理得到：

s表示压缩波P 波波数，r表示剪切波S 波波数。w为圆频率即角频率，k为Rayleigh波波数，B1、B2、C1、C2为任意值.经过推导，得到：

其中，Q1、Q2、Q3、Q4为与孔隙率、渗透系数、密度、拉梅常量、弹性模量、角频率、波数等参数有关的解析式，在附录中给出.

通过上式推导得到P波与S波波数表达式：

根据前人的研究，给定的频率下体波的色散方程通常为带复数的多项式.其中，纵波波数通过求解可得到6 个根kp=Re（kp）+iIm（kp），Re 表示实部，Im 表示虚部.存在3 种压缩波：P1 波、P2 波和P3 波.而本文中的s12、s22，也可解出2 个以上P 波的波数值，求解得到的r值代表剪切波S波的波数，仅有一个.

3 不同模型边界条件的设定

3.1 上覆海水深度Hm且水-土界面不平整

Rayleigh 波在上覆海水的饱和多孔弹性半空间中传播时，其边界条件为：

1）海水表面z=-H处被认为是无应力的，因此，在表面z=-H上的每一点上合力为0，由此可知：

2）界面g（x）处应力分量的能量平衡可以用数学表达式表示为：

3）由界面处压力的连续性z=g（x），可知：

4）根据Kumari 等［17］采用的流体颗粒微极性理论，流体介质中固体颗粒的法向速度和液体的法向速度之和应等于多孔介质的总速度.因此，法向位移连续性表示为：

5）三种不同模型中，z≥0 的土层范围内，土层的变形（剪切膨胀和收缩特性）关系均满足数学公式：

将式（7）、式（8）、式（15）给出的位移分量的期望表达式，代入边界条件式（16）～式（20）中，得到的一个含有6 个未知 数（A1，A2，B1，B2，C1，C2）的 方程组：

为求解方程组式（21），使任意的常系数（A1，A2，B1，B2，C1，C2）均满足方程组式（21）.这也意味着常系数不会影响方程式（21），因此，消去常系数A1、A2、B1，B2、C1、C2，推导得出：

上式即为有上覆海水且水-土界面不平整时的Rayleigh 波的波动方程.其中，aij、aij0（i=1，2，3，4，5；j=1，2，3，4，5，6）为复杂解析式的简化，在附录中提供.

3.2 无上覆海水(H=0)且水-土界面为平面[g(x)=0]

Rayleigh波在无上覆海水的饱和土中传播，其边界条件为：

1）界面z=0 处被认为是自由边界条件的，由此可知：

2）在界面z=0处时，e-rz、e-sz=1，g（x）=c常数时即海水与土体接触界面为平面时的应力分量平衡可以用数学表达式表示为：

3）由界面z=0处孔隙水压力为0：

将式（5）、式（6）、式（13）代入边界条件式（22）～式（25）与式（20）中，得到的一个化简后含有6 个未知数（A'1，A'2，B'1，B'2，C'1，C'2）的方程组：

式中：

式中：aij、bij（i=1，2，3，4，5；j=1，2，3，4，5，6）为推导过程中波数与频率解析式的简化形式，cij（i=1，2，3；j=1，2，3）是与海床参数（渗透系数除外）相关解析式的简化，与M，W，T均在附录中提供.cij与孔隙率、拉梅常数、液体弹性模量、土骨架弹性模量、土颗粒弹性模量等材料参数有关.参数M、W、T与传播介质性质（密度、拉梅常数、弹性模量、土颗粒弹性模量等）参量有关.

单相介质时Rayleigh波角频率与速度方程为：

根据上式计算得到单相介质中的无量纲相速度c/β0为定值，不随波数k1的改变而改变，只与传播介质的材料属性有关.波数与相速度在传播过程中均未产生衰减现象.根据计算得到的角频率w与速度c的关系可知，波速c不随角频率的变化而变化，始终为定值也并未产生衰减，介质的材料参数若未发生改变则波速c保持不变.因此，在本文的模型中，Rayleigh波在均质的单相介质中传播不发生衰减.

3.3 有上覆海水(H≠0)且水-土界面为平面[g(x)=0]

Rayleigh波在有上覆海水的饱和土中传播，其边界条件为：

1）海水表面z=-H处被认为是自由边界条件，因此，在表面z=-H（上表面）上的每一点上合力为0，由此可知：

2）在界面z=0处时，e-rz、e-sz=1，g（x）=c常数时即海水与土体接触界面为平面时的应力分量的能量平衡可以用数学表达式表示为：

3）由界面处压力的连续性z=0，可知在土层中：

4）介质中固体的法向速度和液体的法向速度之和应该等于多孔介质的总速度.因此，法向位移连续性表示为

将式（7）、式（8）、式（15）代入边界条件式（26）～式（29）与式（20）中，得到的1个化简后的含有6个未知数（A''1，A''2，B''1，B''2，C''1，C''2）的方程组：

4 Rayleigh 波在不同模型中的传播与衰减 特性

为了讨论Rayleigh 波在无上覆海水且土层顶部为平面、有上覆海水且水土接触面为平面、有上覆海水且水-土接触面为不平整界面这3 种不同模型中的传播特性，研究孔隙率f、渗透系数K、泊松比υ、弹性模量（E、Es）等土力学参数对Rayleigh 波传播的影响，及各因素对Rayleigh 波诱导下土层的位移、应变和孔隙水压的影响.通过对推导的公式代入数值进行计算，将不同条件下的结果用图线绘制出.参数根据Yew 等［24］的实验结果，并结合Paul 等［25］在饱和多孔半空间的数值模拟中采用的参数进行综合选取.本文中的部分未明确说明的数值分析参数取值如下：

E=6.017×1010Pa，Es=3.6×1010Pa，Ek=4.36×107Pa，Ew=2.0×109Pa，ρw=1 000 kg/m3，ρs=2 650 kg/m3，H=10 m，λ1=0.214×1010N/m2，Rayleigh波波速cr=286 m/s，频率fv=15 Hz.

由于Rayleigh 波可被认为是纵波和横波在半空间自由表面上的叠加［26］，本文也将Rayleigh 波视为横波和纵波的叠加进行计算.

4.1 简化模型Ⅰ

简化模型Ⅰ为无上覆海水（H=0）且水-土接触界面为平面界面［g（x）=0］的简化模型.

表1为对应的计算参数选取表.图2为无上覆水且水-土接触面为平面时不同孔隙率f、渗透系数K下Rayleigh 波波速与频率的关系.其中，蓝色、橙色、黄色曲线分别代表传播介质的孔隙率f为0.1、0.2、0.3 时Rayleigh 波波速随频率的变化关系，可见在E=6.017×1010Pa 等岩石地层参数条件下，孔隙率越低，Rayleigh 波的波速越大.在低频区域，渗透系数K对Rayleigh 波波速的影响较大，渗透系数的值越大，波速越大.随着频率的增加，渗透系数对Rayleigh 波波速影响逐渐减小，超过一定频率后波速趋于稳定.频率100 Hz 以内时，与Liu 等［12］在渗透系数分别为0.005 m/s、0.05 m/s、0.01 m/s 高渗透系数情况下的速度相比，本文在低渗透系数条件下Rayleigh 波的速度更小.图3 所示为简化模型Ⅰ情况下，孔隙率与渗透系数对Rayleigh 波衰减的影响.在岩石地层弹性模量为E=6.017×1010Pa 情况下，地震波频率越高，衰减越快.这与Mahmoodian［18］研究的弹性半空间中不同材料下衰减系数随频率的变化趋势相近，随频率的增加，衰减系数的增加速率逐渐减小，高频区域的衰减系数逐渐趋于稳定.

表1 参数取值表Tab.1 Parameter Choice

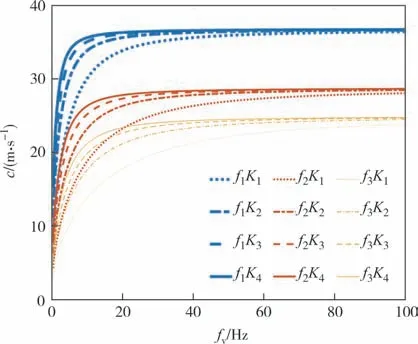
图2 简化模型Ⅰ-频域下孔隙率和渗透系数对相速度的影响Fig.2 Effect of porosity and permeability coefficient on phase velocity in the frequency domain in simplified model Ⅰ

4.2 简化模型Ⅱ

简化模型Ⅱ为有上覆海水（H≠0）且水-土接触面为平面界面［g（x）=0］的简化模型.

图4 为简化模型Ⅱ中不同孔隙率f、渗透系数K下Rayleigh 波波速与频率的关系，图中参数取值可参考表1.从图4 可知，孔隙率与渗透系数对波速的影响规律与模型Ⅰ一致，但在有上覆水的条件下Rayleigh波波速比无上覆水情况下明显更快.

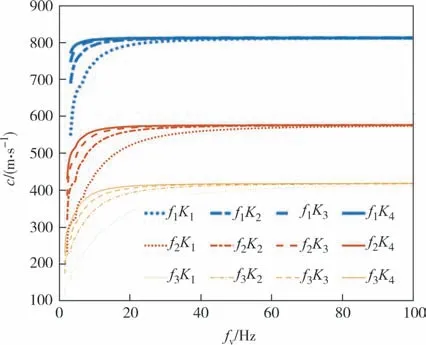
图4 简化模型Ⅱ-频域下孔隙率和渗透系数对相速度的影响Fig.4 Effect of porosity and permeability coefficient on phase velocity in the frequency domain in simplified model Ⅱ

从图5 可知，孔隙率的减小将会使Rayleigh 波波速增加.泊松比υ的变化将影响Rayleigh 波波速，由于泊松比的改变将影响材料其他参数如拉梅常数λ、μ的变化，因此，不能一概判定泊松比大小与波速变化之间的关系，但可以确定的是传播介质材料性质对Rayleigh 波的影响较大，尤其在低波数区域影响更为明显.

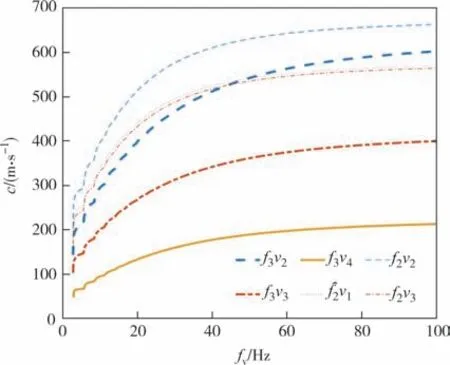
图5 简化模型Ⅱ-频域下孔隙率和泊松比对相速度的影响Fig.5 Effect of porosity and Poisson's ratio on phase velocity in the frequency domain in simplified model Ⅱ

4.3 模型Ⅲ

模型Ⅲ为上覆海水且水-土接触界面为不平整界面的模拟复杂海底模型.图6 所示为模型Ⅲ在不同孔隙率下，Rayleigh 波无量纲相速度c/β0及衰减系数δc/β0随波数k1的变化.孔隙率f的取值分别为0.3、0.35、0.4、0.45、0.5、0.55、0.6.褶皱参数：d=1，p=π/2.其他参数：υ=0.38；E=2.0×106Pa；K=2.0×10-7m/s.从 图6 可知，孔隙率的变化对低波数时Rayleigh 波的无量纲相速度与衰减有明显影响.此规律与Kumari等［17］在考虑孔隙微极性条件下和Xiao等［27］考虑渗流时，计算岩层弹性模量E=6.017×1010Pa 时的规律一致，均是随波数的增大迅速减小后趋于平缓.但此处所用弹性模量适用于软土层而非岩层，在波数0.4＜k＜1 时，大部分相速度c/β0的值小于0，这时Rayleigh波实际并不存在，此波数的取值范围会随着孔隙率的改变而改变.

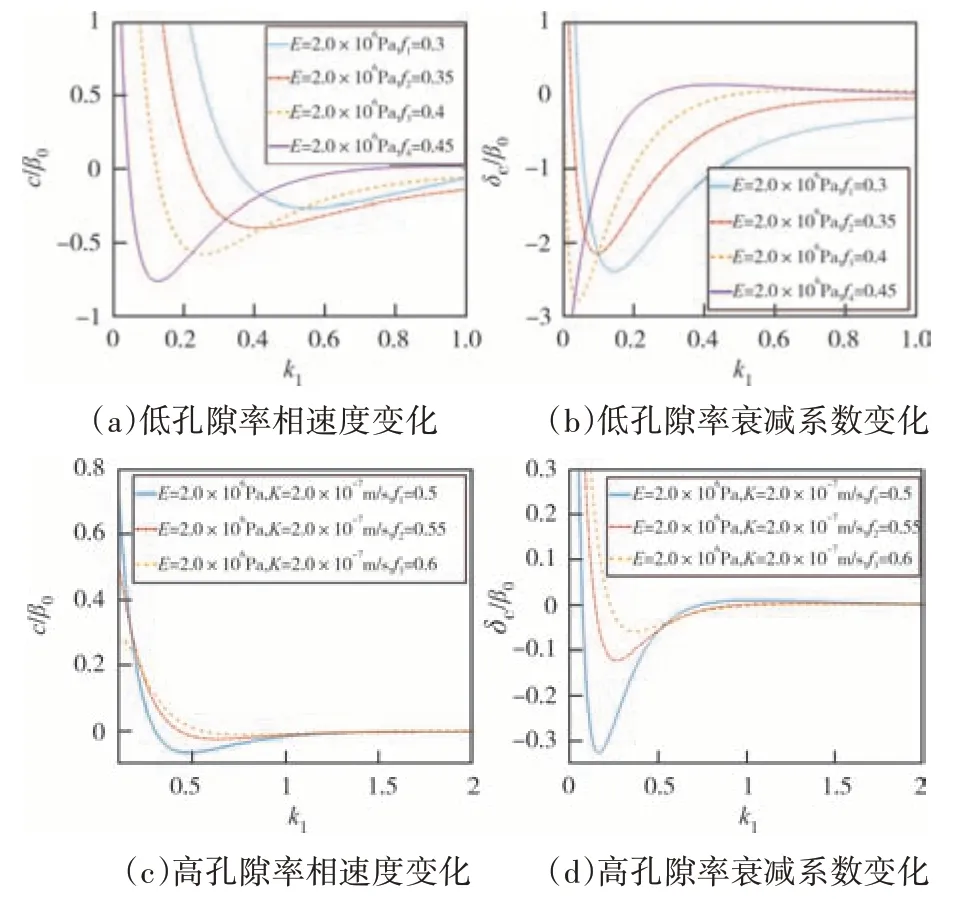
图6 模型Ⅲ-孔隙率对无量纲相速度与衰减的影响Fig.6 Influence of porosity on non-dimensional phase velocity and attenuation in model Ⅲ

图7 所示为模型Ⅲ有上覆海水且水-土接触界面为不平整界面场地时，不同泊松比与渗透系数下的Rayleigh 波无量纲相速度与衰减随波数k1的变化情况.各参数取值为：f=0.3；υ=0.38、υ=0.3；E=2.0×108Pa；K=3.0×10-7m/s、K=4.0×10-7m/s、K=5.0×10-7m/s、

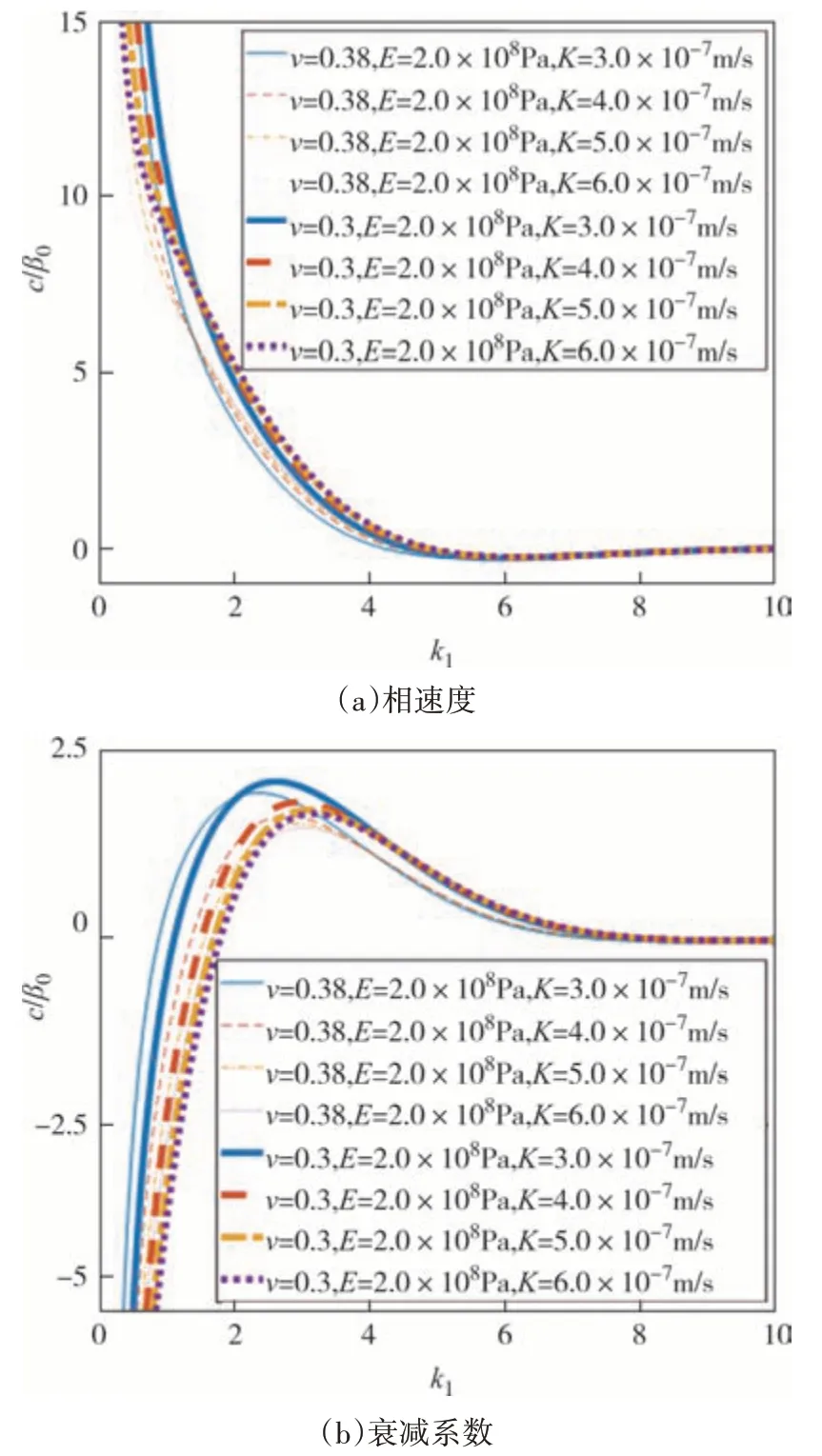
图7 模型Ⅲ-泊松比与渗透系数对无量纲相速度与衰减的影响Fig.7 Influence of Poisson’s ratio and permeability coefficient on non-dimensional phase velocity and attenuation in model Ⅲ

K=6.0×10-7m/s.可知，当波数逐渐增加时渗透系数和泊松比对Rayleigh 波无量纲相速度与衰减的影响逐渐减弱.对比图6 中E=2.0×106Pa 软土地层情况，土体模量的增加，会导致高波数区域中渗透系数K等参数的变化对Rayleigh 波无量纲相速度和衰减的影响增加.由于弹性模量E=2.0×108Pa 取值为砂土地层参数，因此，图7（a）结果与Alam 等［28］在计算扭转波在干砂中传播的结果相近.结合岩层E=6.017×1010Pa 情况可发现，弹性模量越小，无量纲相速度出现负值的概率更大，因此Rayleigh 波易在弹性模量更大的良好地层中出现.此外，Rayleigh 波相速度与衰减与弹性模量、泊松比、拉梅常数等材料性质相关参量有很大关联，这种现象在低波数区即低频区域的影响比较显著.

4.4 Rayleigh波传播影响因素分析

本文将影响Rayleigh 波传播与衰减特性的因素归为两类.第一类是模型自身特性（模型本身的状态，例如：有无上覆海水、水-土界面是否平整以及是否需要考虑介质的多相性），模型本身的状态决定了边界条件的设定，对比图2 和图4 可知，有无上覆海水对Rayleigh 波的相速度影响很大，无上覆海水的饱和土中的波速要明显小于有上覆海水的饱和土.对于无上覆海水的单相介质，通过公式计算得到Rayleigh 波的相速度不随波数改变，Rayleigh 波的传播不发生衰减，即在不考虑能量衰减与阻尼等因素影响的情况下，Rayleigh 波在单一介质中传播波速不变.

第二类为传播介质的参数，例如介质的模量土骨架的弹性模量、土颗粒的弹性模量、渗透系数、孔隙率、泊松比等.由图2～图6 可知，这些参数在低波数区域对Rayleigh 波相速度的影响较大，随着波数的增加即频率的提高影响将逐渐减小.由图6和图7可知，弹性模量与泊松比的改变会影响相速度随波数的变化，弹性模量的增加会提高波数区域其他参数对Rayleigh 波相速度与衰减的影响.更形象地，也就是在高波数区坚硬的岩石对Rayleigh 波诱导下的动力反应要比较软的土层更敏感.

5 Rayleigh 波诱导下海床土动力响应影响因素分析

本节对模型Ⅲ中Rayleigh 波的传播对土体的动力响应影响进行分析，讨论了土体的力学参数（位移、应力、孔隙水压、体变等）随土层深度、渗透系数、孔隙率以及Rayleigh 波波速的变化情况.其中：E=6.017×1010Pa，υ=0.265，f=0.32，K=1×10-4m/s，图表中应力的单位统一为Pa，位移单位为m.

5.1 土层深度的影响

图8（a）～（f）为位于x轴不同位置不同Rayleigh波波速情况下土体的横向位移、水的横向位移、土体x与z方向的剪应力、土体的体变、孔隙水压力随土层深度的变化.由图8 可看出，相同波速下位于x轴不同位置的土体应力应变有差异，这主要是由模型Ⅲ中的水土交界处为褶皱界面导致的.依据文献［29］可知，地震波以不同角度入射会对土体造成不同程度的影响.因此，由于水-土交界面不同程度的起伏使Rayleigh 波入射角度发生改变，位于x轴不同位置产生的结果略有差异.这也说明了考虑水土交界面的不平整程度有益于提高计算的准确性，更切合实际情况［30］.Rayleigh 波对表面土层的影响较大，沿土层深度衰减很快，波速较大的地震波对深层土的影响要大一些，低波速地震波在浅层土中很快衰减.

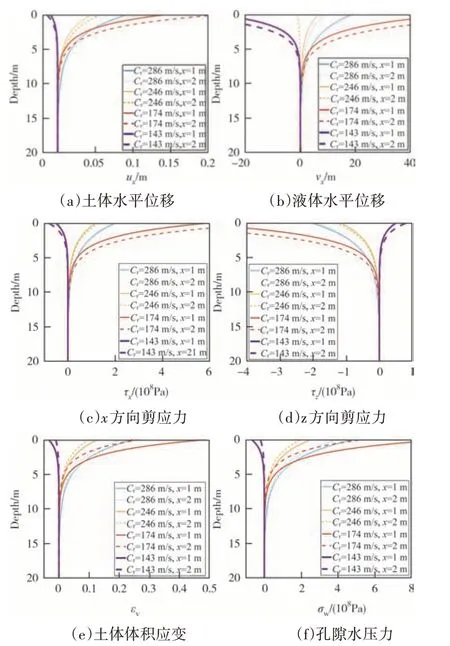
图8 不同横向位置与波速下各力学参数随深度的变化Fig.8 Variation of mechanical parameters with depth at different transverse positions and wave velocities

图9（a）～（d）为位于x轴相同位置不同深度处z=3 m、z=4 m、z=5 m、z=6 m，土体的横向位移、竖向位移、土体的体变、孔隙水压力随波速的变化.可见，随深度的加深，土体的位移、体变与孔隙水压力逐渐减小.由于土层中的各质点进行间歇振动，运动状态随波速频率会有不同，因此图中随波速的增加各参数的峰值起伏不定.

图10（a）～（d）所示为沿x轴不同深度位置的土体体变、孔隙水压、土体与孔隙水的横向位移.由于质点在Rayleigh 波激励下做均匀的间歇振动，因此沿x轴各处孔隙水压与体变呈余弦函数变化，并随土层深度的加深振幅逐渐减小.孔隙水压力峰值约为0.7×108Pa，单位体积的土体产生的剪胀（剪缩）体应变峰值约为0.04 m3.由图10（c）、（d）可知，位于土层深度2 m 位置的土和液体的横向位移最大值分别不超过0.03 m、15 m，幅值随深度加深而减小.从孔压、土体剪胀和剪缩的体积变形εv、位移的减小速率来看，在土层浅层处减小幅度更大，随着土层深度的增加，减小幅度降低.

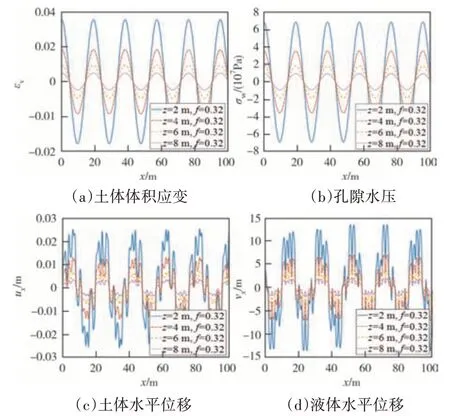
图10 沿x轴不同深度位置各力学参数的变化Fig.10 Variation of mechanical parameters at different depths along the x-axis

5.2 孔隙率的影响

图11（a）～（f）为不同孔隙率下，土层不同深度某一点处的力学参数（土体的横向位移、水的横向位移、土体x轴正应力、剪应力、土体的体变、孔隙水压力）随波速的变化.可以看出，不同孔隙率对于土体和水的位移与应力的峰值影响不同.土体的体变规律与孔隙水压和x轴正应力随波速增加的变化规律相似，不同的仅是数值上的差异.可以推断，此时沿x轴方向的正应力是产生孔压和体变的主要因素之一.

5.3 渗透系数的影响

图12（a）～（d）所示为不同波速下，土体的横向位移、土体x轴剪应力、孔隙水压力随渗透系数的变化.由图12可知，低渗透系数下（K＜10-6m/s）渗透系数的增加对土层各力学参数的影响较大，但当渗透系数增大到一个定值时，渗透系数的增加将不会影响土层各力学参数的值.但是，从图12 中仅能确定Rayleigh 波波速的改变对土层应力应变等参数有影响，不能确定波速的高低对土层各参数的影响规律.

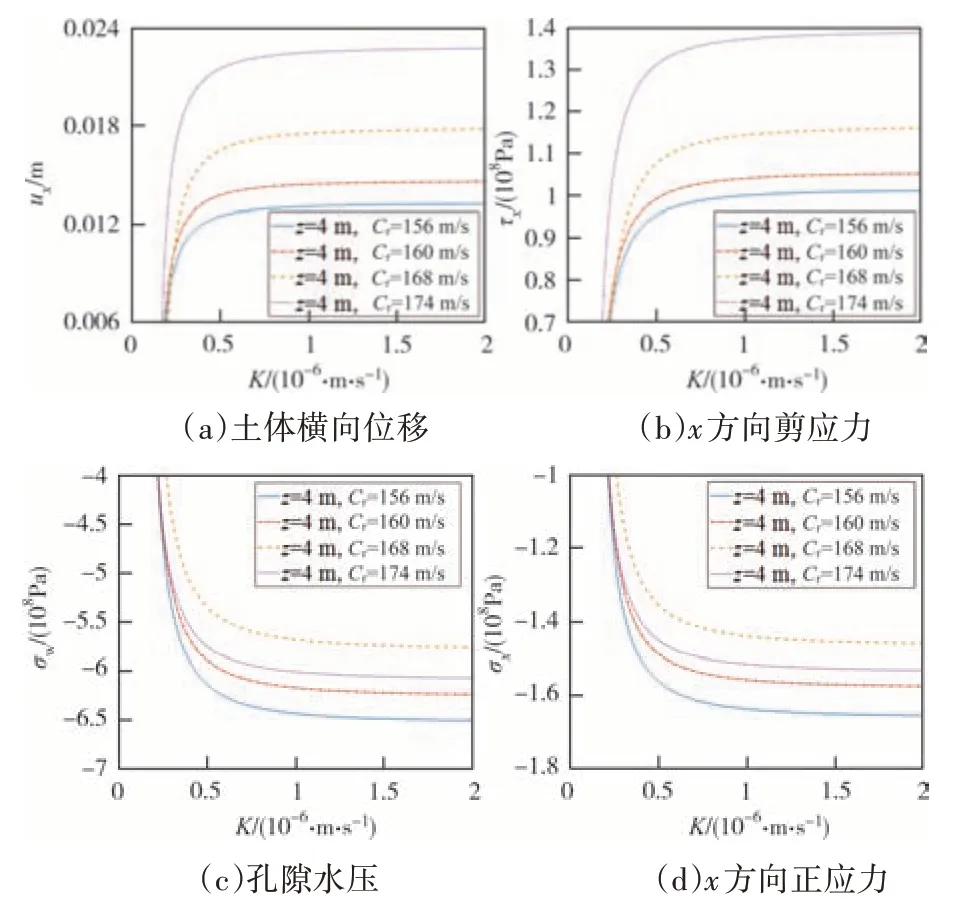
图12 土体各力学参数随渗透系数的变化Fig.12 Variation of mechanical parameters of soil with permeability coefficient

6 结论

本文建立了Rayleigh 波在不同模型中传播的数学模型，分析了Rayleigh 波在上覆海水且水-土界面为不平整的场地、上覆海水且水-土界面为平面的场地、无上覆海水的饱和场地与单相介质土层中的传播与衰减特性，并针对上覆海水且水-土界面不平整的场地动力响应影响因素进行分析，得到了以下结论：

1）模型自身与边界条件的设定对Rayleigh 波传播的影响很大，Rayleigh 波在无上覆水且水-土界面为平面的模型中的传播速度要远小于有上覆水模型中的传播速度.综合软土E=2.0×106Pa、砂土E=2.0×108Pa、岩石E=6.017×1010Pa 三种不同地层情况可以发现，软土地层中无量纲相速度出现负值的概率更大，而砂土和岩层相速度基本为正值.可知Rayleigh波易在弹性模量更大的良好地层中出现，软土地层不利于Rayleigh波的产生与传播.

2）渗透系数、孔隙率、泊松比对低频率、低波数区域Rayleigh 波相速度与无量纲相速度的传播影响较大.随着频率、波数的增加，Rayleigh 波相速度将逐渐维持稳定，相同孔隙率、不同渗透系数下的Rayleigh 波的波速将维持在同一定值.土体弹性模量的增加会扩大渗透系数、孔隙率f等参数在高波数区对Rayleigh波无量纲相速度和衰减的影响.

3）Rayleigh波在地表浅层衰减极快，随着土层的深度加深，对土层应力应变变化的影响逐渐减小.水-土界面的不平整状态对土体浅层的应力应变影响较大.孔隙水压和土体剪胀和剪缩的体积变形变化规律一致，说明孔压对土体变形起着至关重要的作用.

4）Rayleigh 波波速、孔隙率、渗透系数均是影响土层应力、变形与孔压变化的因素.其中，Rayleigh波波速越大，对深层土体的影响也越大.在低波数（低频）时渗透系数会对Rayleigh 波传播速度、衰减特性以及土层的各力学参数造成明显影响，随渗透系数的增加影响变小.波速以及土体弹性模量的变化，会改变孔隙率和渗透系数对土体应力应变等力学参数的影响程度.