基于车桥接触点响应和盲源分离的桥梁模态识别
2023-06-03李岩施雪晴刘文
李岩,施雪晴,刘文
(1.哈尔滨工业大学 交通科学与工程学院,黑龙江 哈尔滨 150090;2.上海市政工程研究总院(集团)有限公司 贵阳分公司,贵州 贵阳 550002)
桥梁健康监测常规方法,是通过安装在结构上的传感器系统获取桥梁的动态信息,进行结构状态评估.该类方法目前主要针对悬索桥、斜拉桥等大跨度复杂体系大型桥梁,可实现结构状态实时监测,但其传感系统更换复杂且费用很高.对于道路网络中占比最大的中小跨径桥梁,近年来基于车辆响应的桥梁间接测量法正获得越来越多的关注.采用这类方法,有望实现对中小型桥梁整体状态的快速评估,可大幅提高检测效率和经济性.
移动车辆过桥时车辆与桥梁发生耦合振动,车辆动力响应中会包含桥梁结构信息,因此桥梁结构状态的改变将导致车辆响应受到影响.基于该原理,Yang等[1]在2004 年提出通过安装在测试车上的传感器进行桥梁状态评估和诊断的间接测量法(又称车辆扫描法)技术构想并开展了相关研究.近年国内外学者针对该方法开展了大量研究工作并取得了丰富成果.2021 年杨永斌等[2]在对该方向的研究综述中分析指出,桥面不平度仍是利用车辆扫描法进行桥梁模态参数识别和状态评估所面临的主要问题和挑战;Chang等[3]从理论上推导了考虑桥面不平度条件下过桥车辆响应的近似解,结果表明桥梁信息会被不平度影响覆盖从而难以识别;Yang等[4]基于双梁轨道模型的间接测量发现,对于平滑轨道,桥梁一阶频率易于识别,考虑轨道不平顺后桥梁一阶频率的识别难度大大增加;贺文宇等[5]提出一种基于间接法识别桥梁振型的损伤定位指标,试验结果表明当路面粗糙度等级为B或C时,桥梁振型识别准确性很差.
一些学者尝试多种方式滤除桥面不平度对基于车辆响应的桥梁模态识别方法的影响:Toshinami等[6]考虑桥面不平度影响实现了桥梁基频的识别;Yang 等[7]提出采用两辆完全相同的小车组成测试车系统,在频域上对前后两车效应相减,以滤除桥面不平度效应的方法;Kong 等[8]提出在时域上对参数相同的两车的加速度效应相减,再进行傅立叶变换滤除桥面不平度的策略;Yang等[9]发现适当的车辆阻尼可降低不平度的干扰;张彬[10]研究发现增加车辆的重量在一定程度上可减少桥面不平度的影响;Yang等[11]采用双自由度车辆模型在考虑桥面不平度条件下识别出桥梁第二阶频率;Nayek等[12]使用输入估计方法获得车桥接触点响应,进而开展模态识别研究发现,桥面不平度对桥梁低阶频率识别精度有较大影响;阳洋等[13]利用两辆质量、刚度等参数具有特定关系的小车前后驶过桥梁,对其加速度响应积分得到位移响应并做差以去除不平度的的影响,开展了桥梁模态识别研究.
综上所述,现有研究所提出的方法一定程度上能滤除桥面不平度的影响,并识别得到一些桥梁模态信息,但普遍存在高阶模态信息识别准确性差的问题;同时采用较多的前后车响应相减策略中,需要前后两车参数相同且行驶迹线完全重合,但这种理想化假定增加了方法实际应用的难度.可见,针对基于移动车辆响应的桥梁模态识别,研究更加有效的处理和滤除桥面不平度影响的新方法十分必要.为此,本文以间接测量法既有研究成果为基础,基于车桥接触点响应中桥面不平度效应与桥梁振动效应在空间上具有独立性的特征,考虑桥面不平度影响,提出针对车桥接触点响应的盲源分离(Blind Source Speration)处理策略.应用二阶盲识别(Second Order Blind Identification,SOBI)算法,以两组车桥接触点加速度响应信号作为输入信号,并对其进行预白化处理,求解解混矩阵与输入信号相乘获得桥梁振动信号的估计信号,有效滤除了桥面不平度的影响,实现了桥梁多阶模态频率和振型的识别.采用数值仿真算例对所提出方法的准确性和适用性进行了验证,并开展了多种关键参数对方法的影响分析.
1 基于车桥接触点响应盲源分离的桥梁模态识别方法
1.1 车桥接触点响应的间接估计
既有研究表明,车桥接触点响应中无车辆频率成分,基于车桥接触点响应进行桥梁模态识别可以避免车辆频率的干扰[1].由于实际测量中一般无法直接测得车轮和桥梁接触点处响应,针对单自由度车辆模型,本文采用中心差分法,利用车体加速度响应对车桥接触点加速度响应进行估计,如式(1)所示,将其与式(2)所示的单自由度车辆运动方程联立,可得到车桥接触点加速度响应.
式中:mv为车辆质量;t为车辆运行时间;i表示第i时刻.通过该法估计车桥接触点响应的准确性将在后文结合数值算例进行验证.
1.2 车桥接触点响应盲源分离信号处理算法
为解决桥面不平度对基于车桥接触点响应进行桥梁模态识别的影响问题,提出采用二阶盲识别(SOBI)算法滤除车桥接触点信号中的桥面不平度影响的方法,具体流程如图1所示.

图1 基于SOBI估计桥梁振动源信号的流程Fig.1 The process of estimating bridge vibration signal based on SOBI
盲源信号分离(Blind Source Speration)[14]是指对于直接采集到的由多个源信号混合形成的信号进行处理,从中分离出相对独立源信号的过程.车桥耦合振动系统中车体和车桥接触点响应信号均可视为由未知源信号组合得到.对车辆子系统来说,输出为车体振动信号,输入为桥梁振动和桥面不平度,这两种输入信号具有非依赖性(统计独立性、不相关性)、非高斯性(至多一个高斯分布)、非平稳性和非白性(频域非平稳性),满足盲源信号分离对于源信号的基本假设[15].根据源信号混合过程,盲源信号分离问题可分为线性混合问题与非线性混合问题,而线性混合问题又可分为瞬时混合信号盲分离和卷积混合信号盲分离两类.本文所涉及的车桥接触点响应信号可视为由桥梁振动和桥面不平度经线性叠加得到,属线性混合问题.
线性盲源分离系统模型如图2 所示,其中s(t)=[s1(t),s2(t),…,sn(t)]T,表示n个源信号,各源信号间满足非依赖性假设;x(t)=[x1(t),x2(t),…,xm(t)]T,表示m个观测信号,需满足m≥n;x(t)由s(t)经线性混叠组成,即x(t)=As(t),其中A为m×n阶系统混合矩阵.盲源分离是在仅已知观测信号x(t)条件下,求解解混矩阵B,使得y(t)=Bx(t)是未知源信号s(t)的最优逼近.
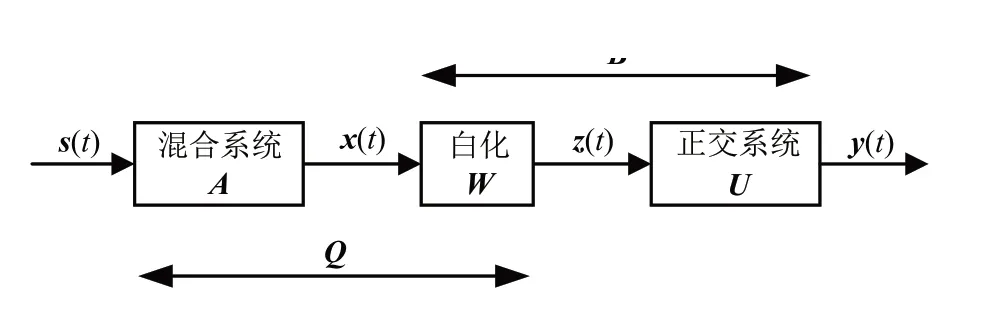
图2 线性盲源分离系统模型Fig.2 Linear blind source separation system model
本文采用盲源分离中基于信号二阶统计量分解线性混合信号的二阶盲识别(SOBI)算法,具体实现过程如下:
1)对一组车桥接触点竖向加速度响应信号x(t)进行预白化处理.
a)由观测信号估计零时间延迟相关矩阵:Rxx(0)=E[x(t)xT(t)].
b)对Rxx(0)进行奇异值分解:Rxx(0)=UΛUT,则预白化矩阵为,其中Λ为对角矩阵,主对角线元素为Rxx(0)的奇异值,其余元素为0.
c)经预白化处理后信号变为z(t)=Wx(t),z(t)与源信号s(t)之间的关系为正交变换.
2)求解解混矩阵.
a)定义延 时相关阵Rs(τ)=E[s(t)sT(t+τ)],Rz(τ)=E[z(t)zT(t+τ)],取τ为一组 不同值τ1,τ2,…τp,得到一组Rz(τi)的估计,i=1,2,…,p.
b)定义矩 阵Q满 足z(t)=Qs(t),由Rzz(0)=E[z(t)zT(t)]=QE[s(t)sT(t)]QT=I可得知Q是正交归一阵,Rs(τi)=QTRz(τi)Q,i=1,2,…,p.可对Rz(τi)进行联合对角化逼近求取Q.
c)求得解混矩阵B=QTW.
3)根据如图2所示关系计算得到桥梁振动响应估计信号:y(t)=Bx(t).
1.3 基于信号带通滤波和Hilbert变换的桥梁模态识别
基于经SOBI 算法分离获得的桥梁振动响应时域信号,通过傅立叶变换获得频域信号并对信号峰值对应频率进行提取,得到桥梁各阶频率.采用带通滤波器分离出各阶频率成分对应的信号,进行Hilbert变换,获得桥梁各阶振型.
带通滤波方法通过对桥梁振动响应信号进行滤波,滤去不需要的频率对应波形,留下桥梁振动各阶频率对应波形.具体做法是将经傅立叶变换得到的桥梁振动频域信号进行各阶频域筛选,根据识别得到的桥梁振动频率,截取各阶频率范围内的信号序列,对其进行逆傅立叶变换,得到该段频率范围对应的一组新的时间序列信号,记为s(t),为保证后续振型识别效果,截取频率范围不宜过大,一般取1~ 2 Hz.
Hilbert 变换是将一个连续时间信号与具有脉冲响应h(t)=1/πt的线性时不变系统作卷积后输出信号的过程.现有各阶频率对应的时程信号s(t)经变换后变为:
1.4 基于支点数据延拓的振型修正
由于Hilbert 变换方法存在端点处频谱泄露现象,且车辆作用下桥梁支点附近梁体振动响应相对较小,导致支点位置附近振型识别误差较大.为解决该问题采用支点单元数据延拓的方式进行振型识别修正[13].通过已获得的远离支点位置数据对支点及支点以外数据进行估计,延拓原理如图3 所示.具体做法如下:1)选取远离支点的一组振型数据,考虑到距离支点越近振型识别误差越大,因此需结合桥梁实际长度综合考虑.2)计算得到已选振型数据关于支点中心对称的反对称点数据,从而增加振型识别有效数据数量,提高有效数据在数据总体中占比,达到减小支点附近识别误差的目的.3)对延拓后新数据进行曲线拟合,选取支点间部分曲线作为修正后的振型.
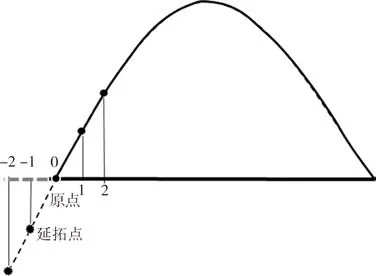
图3 振型支点数据延拓示意Fig.3 Schematic diagram of modal data extension on support position
1.5 基于车桥接触点响应与盲源分离方法的桥梁模态识别方法框架
基于前述的原理和方法,建立了基于车桥接触点响应与盲源分离方法的桥梁模态识别方法框架,如图4所示.主要实施步骤如下:
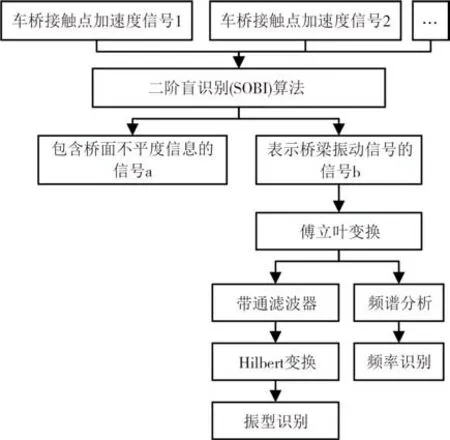
图4 桥梁模态识别框架Fig.4 Bridge modal identification framework
1)根据实测车体加速度响应信号(两组或两组以上),采用中心差分法估计车桥接触点竖向加速度响应信号.
2)将得到的车桥接触点加速度响应信号采用二阶盲识别(SOBI)算法分离桥面不平度与桥梁自身振动信号.
3)对得到的桥梁振动信号进行傅立叶变换获得振动频域信号,据此进行桥梁频率识别.
4)采用带通滤波和Hilbert变换进行桥梁振型识别并作修正.
需要说明的是,上述基于车桥接触点响应的桥梁模态识别方法主要适用对象为中小跨径桥梁.
2 数值算例
2.1 算例基本参数
跨度25 m 简支梁桥,单位长度质量2 000 kg/m,主梁弹性模量27.5 GPa,截面惯性矩I=0.15 m4,截面面积S=1.8 m2,有限元模型梁单元划分尺度为0.1 m,共250 个单元,阻尼比取为0.05.建立桥梁的空间梁单元计算模型并进行模态分析得到结构的前3 阶频率为3.60 Hz、14.33 Hz、31.95 Hz.采用SOBI 进行混合信号处理求解源信号时,需观测信号不少于源信号数量.车辆接触点响应包括桥面不平度和桥梁振动2个源信号,故算例采用参数相同的 2辆车过桥以获取2 组车桥接触点响应数据.车辆质量mv=1 000 kg,刚度kv=200 kN/m,不考虑阻尼,频率为2.25 Hz.过桥时两车间距1 m,速度2 m/s.桥面不平度取“好”,车辆与桥梁关系示意图如图5 所示.车桥耦合数值仿真时程分析时间步长为0.001 s,采用课题组自编的车桥振动程序[16-17]进行上述数值仿真模拟.上述算例及有限元建模参数等选取与文献[18]一致,文献[18]中已通过模型试验对桥例有限元模型及动力分析结果正确性进行了验证,由此也可间接表明本文上述建立的桥例有限元模型及动力特性分析结果的正确性.
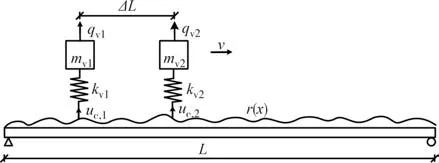
图5 车辆与桥梁关系示意图Fig.5 Relationship of vehicle and bridge
以两车车体响应估计得到的车桥接触点加速度响应信号作为两组已知混合信号,采用SOBI 算法进行分离,联合对角化的时延个数取10,通过本文前述的模态识别分析方法和流程,求解两组估计源信号.
2.2 车桥接触点响应估计与信号盲源分离
2.2.1 接触点响应估计
图6 为采用车体加速度中心差分法估计的两车车桥接触点加速度,二者将作为盲源分离的输入信号.取车1 的车体加速度中心差分法估计的车桥接触点加速度信号,与直接提取的车桥接触点处桥面加速度进行对比,结果如图7 所示.从图7 可见二者一致性良好,表明所采用的车桥接触点加速度响应估计方法具有较高的准确性,可用于后续识别分析.
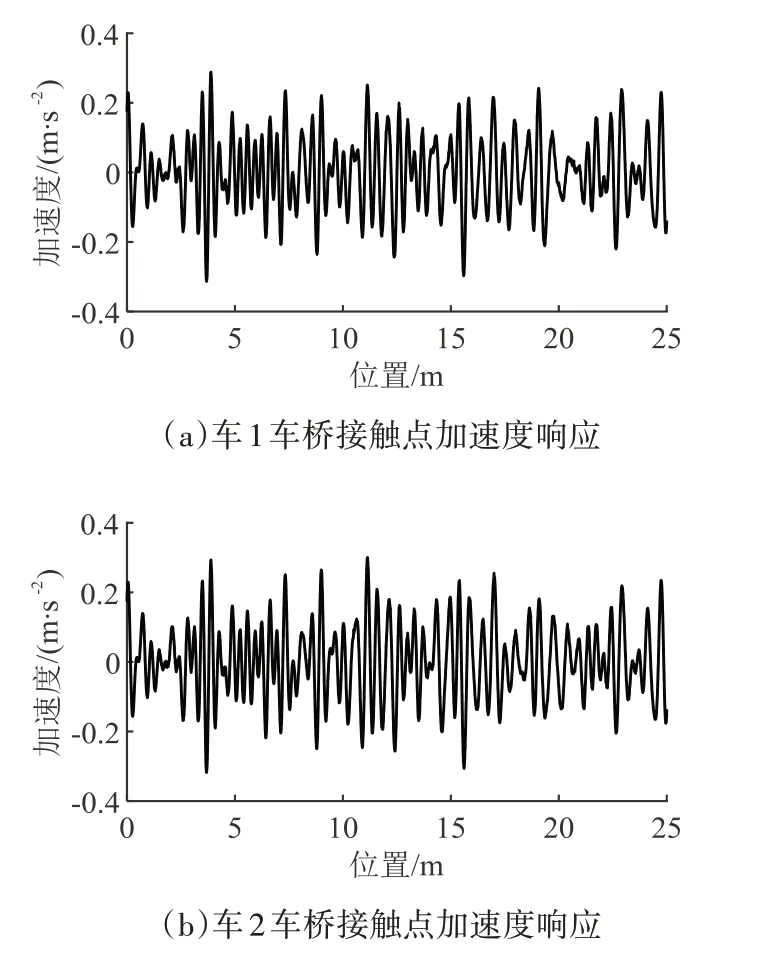
图6 车桥接触点加速度响应Fig.6 Acceleration response of vehicle-bridge contact point
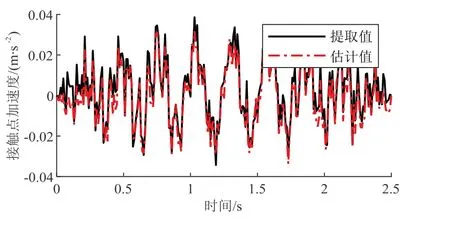
图7 接触点加速度时程响应对比Fig.7 Comparison of contact point acceleration response
2.2.2 信号盲源分离结果
两组车桥接触点响应经过前述提出的SOBI 分离方法处理后,得到两个源信号的时域图和频域图如图8 所示.可以发现,图8(c)源信号1 频域分布随机性较强,为不平度效应,图8(d)源信号2 频域分布规律为桥梁振动效应.同理,源信号1的时域图[图8(a)]也表现出分布随机性,源信号2 的时域图[图8(b)]呈现振幅先增大后减小的规律,为估计的桥梁振动信号.
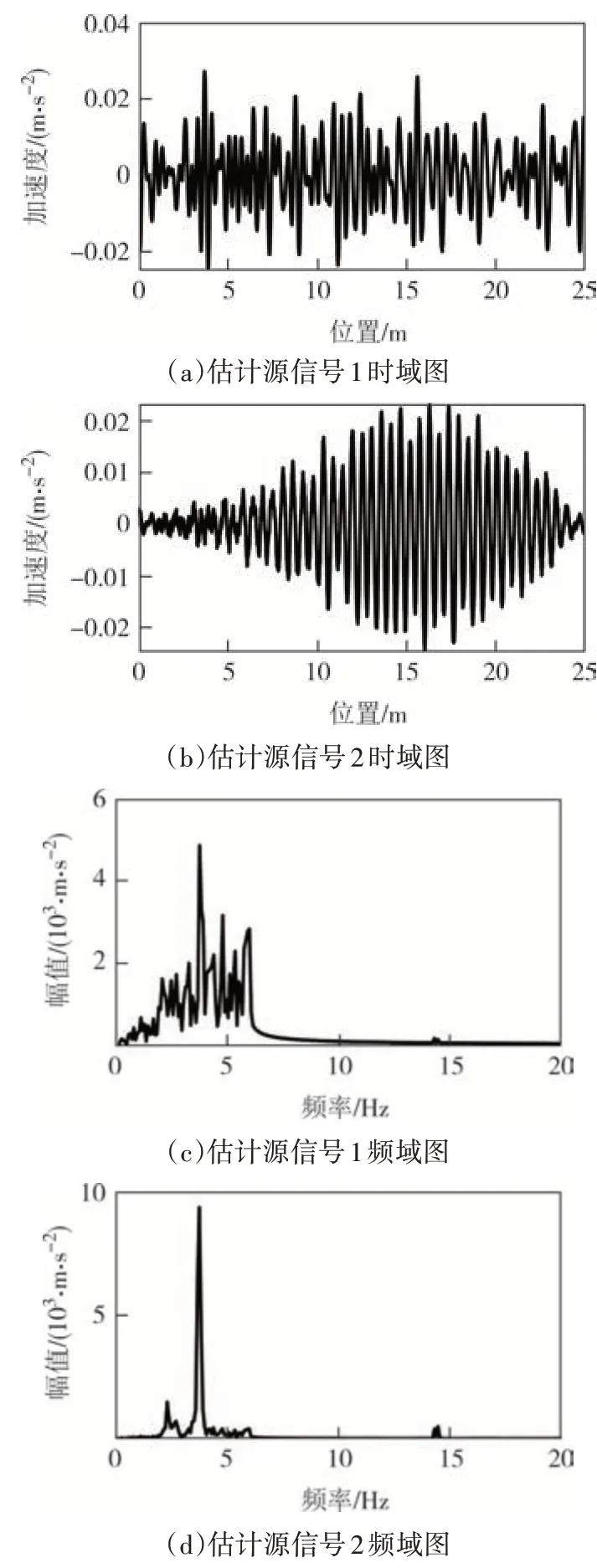
图8 SOBI估计源信号Fig.8 Estimated source signals based on SOBI
将源信号2 与车辆2 行驶过程中对应车桥接触位置的桥梁振动信号在频域上进行对比,将其按照各自最大值进行归一化,结果如图9 所示.可见二者频域分布基本一致,表明SOBI 处理后得到的源信号2基本滤除了不平度的影响.
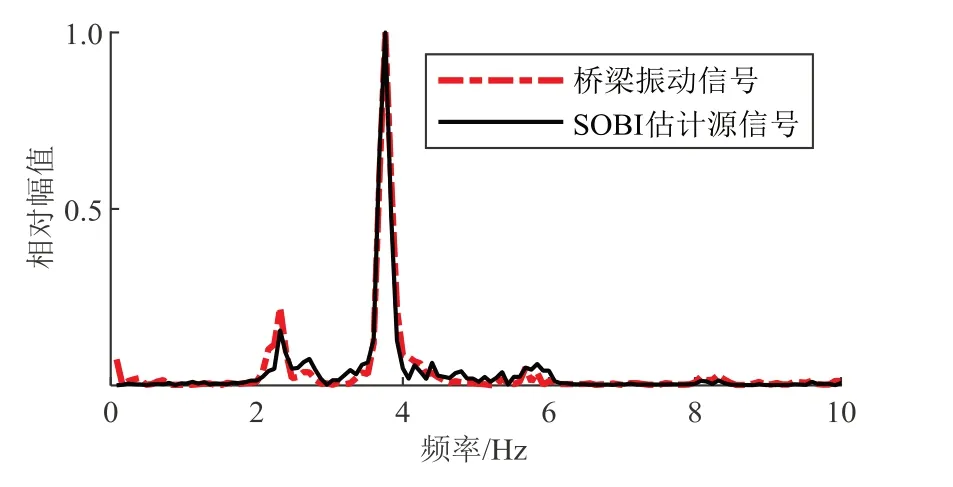
图9 加速度信号频谱分析对比Fig.9 Comparison of spectrum analysis for accelerations
为考虑实际测量中可能存在的噪声干扰,通过在车辆加速度响应信号中加入信噪比为20 dB 的高斯白噪声模拟其影响.采用SOBI处理得到考虑噪声前后的源信号频域对比如图10(a)所示,可见白噪声对源信号的估计产生了影响.信号经滤波器滤除高频噪声后得到的估计源信号频域对比如图10(b)所示,可见此时和未引入白噪声前信号频域分布基本一致,表明以上方法可有效去除测试噪声的影响,白噪声对使用SOBI 估计源信号的影响基本可忽略不计.
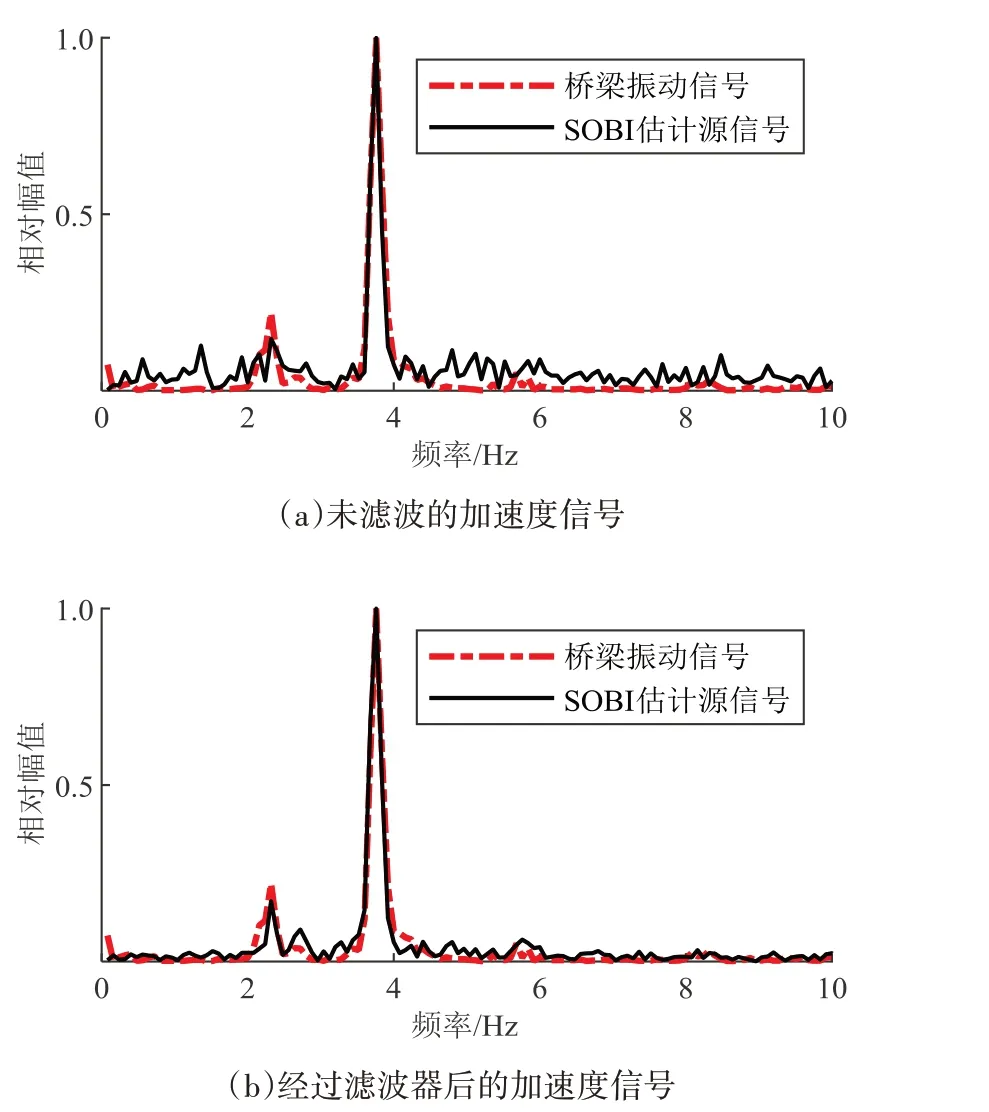
图10 考虑噪声的频谱对比分析Fig.10 Spectrum comparison and analysis under noise
2.3 基于车桥接触点响应的桥梁模态识别
基于估计源信号2 的频谱分析结果,可识别得到前3 阶频率.桥梁高阶频率有明显双尖锋现象,取其平均值作为频率识别结果.对SOBI处理获得的源信号采用带通滤波器及Hilbert变换识别得到桥梁前5阶振型.模态识别结果如图11所示,频率相对误差及振型MAC 值见表1.频率识别值与理论值相对误差为0.03%~4.44%,振型识别仅在支点处存在一定误差.分析该误差产生原因:首先是支点处振动较小,导致车辆测得振动信号较弱,造成结果分辨率相对较低;其次全桥处于同等不平度状况下,支点附近车辆响应中受桥面不平度影响占比较大,导致信号分离过程中会产生一定误差;此外车桥接触点响应间接获取计算过程存在一定的小幅误差,这对支点处振型提取也存在一定不利影响.考虑到梁端位置模态振型值对桥跨振型识别结果MAC 值贡献很小,且总体上MAC 值在0.99 以上,表明该识别结果可满足实际动力测试工程精度要求.
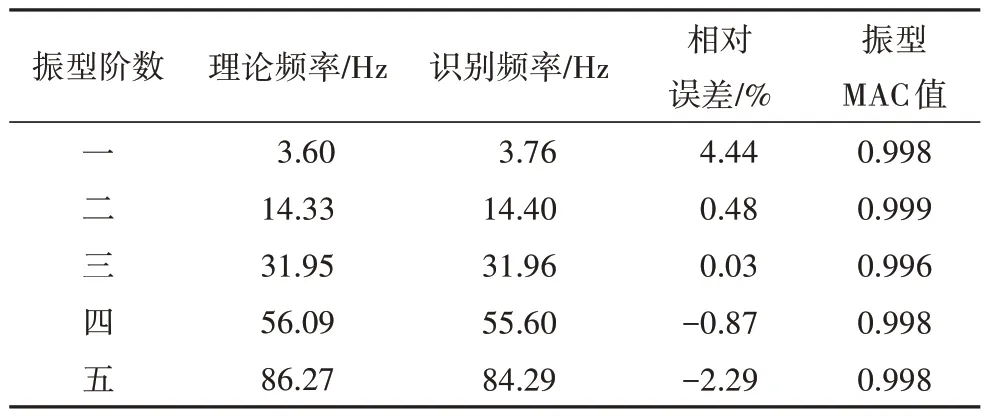
表1 桥梁频率与识别振型MAC值Tab.1 Identified frequences of bridge and MAC of modes
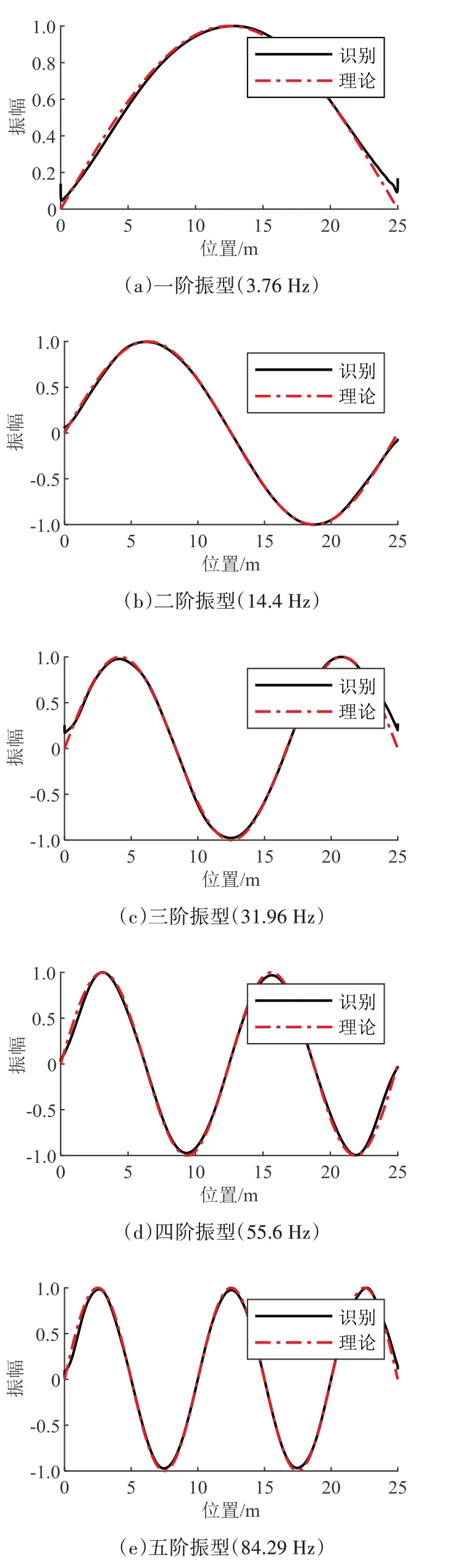
图11 振型识别结果Fig.11 Identified modes of bridge
3 影响参数分析
既有相关研究表明,测试车间距、桥面不平度状态、车辆自振频率及车辆行驶速度[19-20]是影响基于移动车辆动力响应进行桥面模态识别的主要参数.为此,考虑上述4 个参数对所提出桥梁模态识别方法的影响,进行分析研究.
3.1 车辆间距的影响
考虑两辆检测车间距从0.5 m 到3.5 m,每1 m 增幅设置一个工况,其余参数与2.1 节所述参数相同,基于前述所提出的方法进行桥梁模态识别.不同车辆间距工况下桥梁频率识别结果见表2.随着车辆间距增加各阶频率识别结果基本保持一致,表明所提方法对测试车间距不敏感.
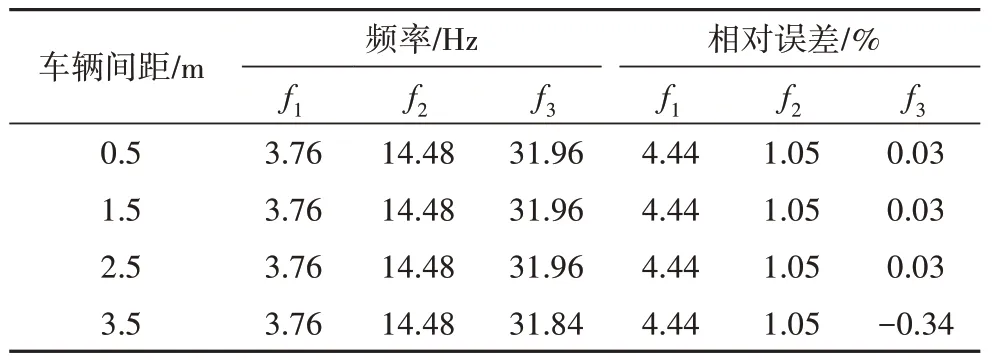
表2 不同车距下桥梁频率识别结果Tab.2 Identified frequencies of bridge under different vehicle distances
各阶振型MAC 值如图12 所示,对第1 阶振型,随车辆间距的增大MAC 值呈增长趋势,识别误差减小;对第2、第3阶振型,随车辆间距增大MAC值逐渐减小,识别误差增大.总体上不同车辆间距下的MAC 值均在0.97 以上,车辆间距的增大对高阶振型识别精度会产生不利影响.
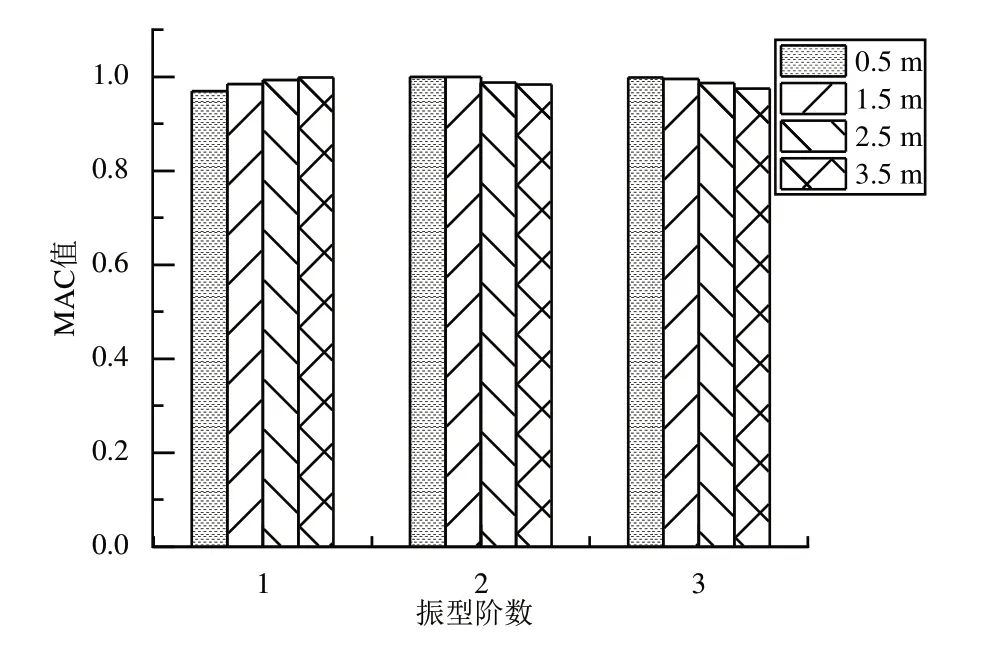
图12 车距对桥梁识别振型MAC值的影响Fig.12 Influence of vehicles distance on MAC of bridge identifien models
3.2 桥面不平度的影响
采用和前述算例相同的桥梁和车辆参数,车辆以间距2 m 通过桥梁,考虑“很好”“好”“一般”和“差”4 种桥面不平度状况.桥梁频率识别结果见表3,识别得到各阶振型MAC值如图13所示.
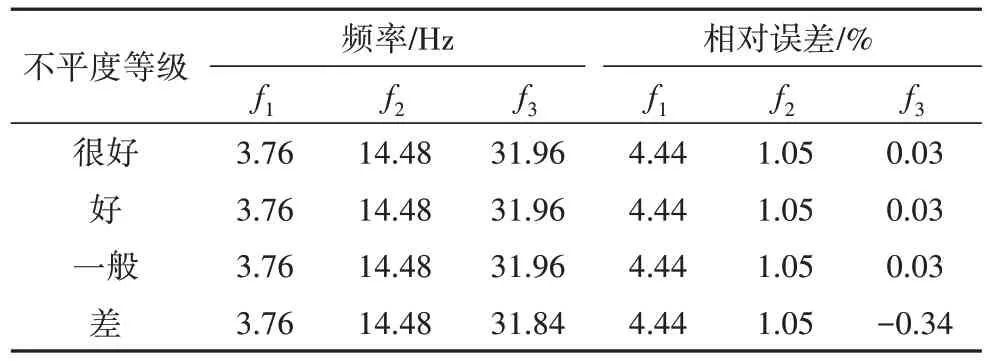
表3 不同桥面不平度下桥梁频率识别的结果Tab.3 Identified frequencies of bridge under different deck roughness
由表3 可见,桥梁不平度状况对各阶频率的识别结果基本无影响.由图13 可见,第1 阶振型MAC值随桥面不平度劣化整体呈下降趋势,当桥面不平度为“差”时,振型MAC 值降为0.93;第2、第3阶振型MAC 值随桥面不平度劣化变化不大,最小值为0.97.综上,不同桥面不平度等级条件下,基于所提出的方法均可较为准确地分离桥面不平度效应与桥梁振动,进而实现桥梁频率和振型识别.桥梁模态识别误差对桥面不平度等级变化不敏感,所提出的模态识别方法在各级桥面不平度等级下都具有较好的稳定性.
3.3 车辆频率的影响
通过改变车辆弹簧刚度的方式设置多种车辆频率,车辆其余参数保持不变.当车辆刚度分别为100 kN/m、200 kN/m、350 kN/m、500 kN/m 时,对应车辆频率分别为1.59 Hz、2.25 Hz、2.98 Hz、3.56 Hz.采用所提方法进行桥梁模态识别,各工况下桥梁频率识别结果及振型识别结果分别如表4和表5所示.
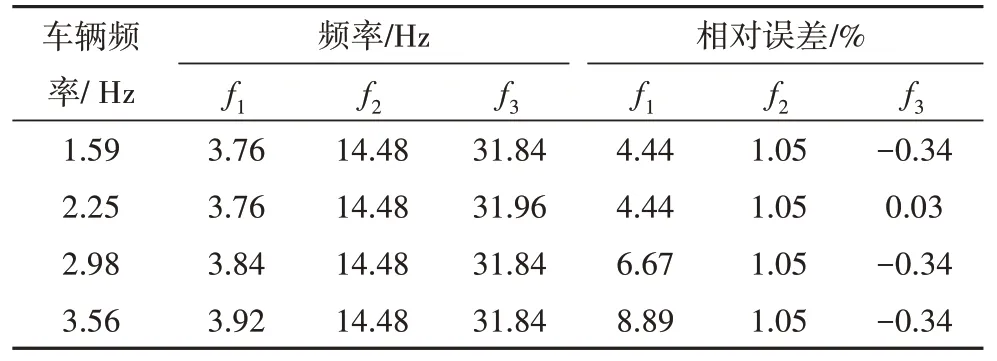
表4 不同车辆频率(刚度)下桥梁频率识别结果Tab.4 Identified frequencies of bridge under different vehiclular frequencies(stiffness)
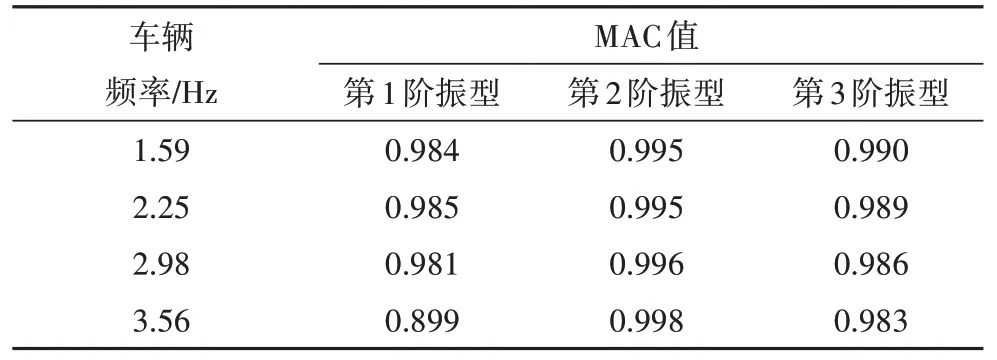
表5 车辆频率对桥梁识别振型MAC值的影响Tab.5 Influence of vehicular frequency on MAC of bridge identified modes
从表4 可见,当车辆频率(刚度)增加时,桥梁基频识别误差逐渐从4.44%增加到8.89%,其余各阶频率识别误差无明显变化.从表5 中可看出,随着车辆频率(刚度)增加,第1阶振型MAC 值呈下降趋势,当车辆频率(3.56 Hz)接近桥梁频率(3.60 Hz)时,1 阶振型MAC 值变为0.899;第3 阶振型MAC 值也呈下降趋势.表明当车辆和桥梁频率接近或重叠时,本文所提出的盲源分离方法有效性将受到影响,在确定检测车辆设计参数时应尽量使车辆频率远离桥梁频率范围.
3.4 车辆行驶速度的影响
采用和前述算例相同的桥梁和车辆参数,在车速10 km/h、30 km/h、50 km/h 情况下采用前述方法获得桥梁的频谱如图14 所示.可见随着车速增加,桥梁频谱变得更为粗糙,但仍可通过峰值位置识别各阶频率,但桥梁基频识别误差随着车速提高而增大.这主要是由车速增大后车辆所采集到的响应信号长度变短、包含的桥梁振动信息变少所致,建议实际应用时控制车速不超过30 km/h为宜.
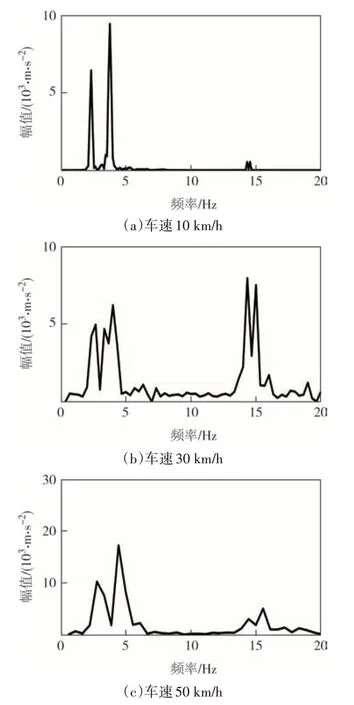
图14 不同车速下识别的桥梁频谱图Fig.14 Spectrum diagram of bridge at different speed
4 结论
将盲源分离理论应用于间接测量中,提出了基于车辆响应的桥梁模态识别方法.依托数值算例对所提出方法的适用性和有效性进行了验证,系统分析了多种参数对方法适用性的影响,得到以下结论:
1)所提出的基于二阶盲识别(SOBI)进行车辆响应处理方法,可有效滤除桥面不平度影响,且滤除效果不受桥面不平度等级影响.
2)针对所提模态识别方法的影响参数分析结果表明:车辆间距和桥面不平度状况对桥梁模态识别结果基本无影响;当车辆频率接近桥梁频率时,桥梁模态识别精度明显下降,建议通过设计测试车辆的频率远离桥梁频率来保证模态识别精度;测试车辆车速不宜过高,建议不超过30 km/h为宜.
3)基于车辆响应盲源分离策略的桥梁模态识别方法,考虑不同车辆间距、桥面不平度等级和车辆频率条件下都具有良好的适用性和鲁棒性,可实现桥梁多阶模态较高精度的识别.
