桥梁车辆荷载效应外推组合极值方法适用性比较研究
2023-06-02赵鑫莹金泽人
阮 欣, 赵鑫莹, 金泽人
(同济大学 土木工程学院,上海 200092)
中小跨径桥梁跨度小、桥面宽度窄,加载范围内车流场景较单一[1]。对于这类由单一加载车流产生的荷载效应,传统的极值计算方法有较好的适用性[2-4]。随着跨径的增长和桥面宽度的增加,桥上车辆荷载的分布趋于复杂,多个车流加载事件的混合逐渐成为车辆荷载效应极值的主要控制因素。多事件混合影响下的车辆荷载效应呈现非同一分布特征,采用单一极值分布无法准确拟合混合车流下荷载效应的底分布,从而引起极值外推结果的较大误差。针对这种复杂情况,组合极值推定方法被提出。
组合极值方法将复杂样本划分为多个符合单一极值分布的子样本的组合,通过组合概率理论计算复杂样本的分布模型,并由此外推极值。组合极值方法能够很好的解决传统极值理论不适用于非同一底分布样本的问题[5-11]。Caprani等[8]结合若干理论实例,验证了组合广义极值法(combined generalized extreme value method,CGEV)方法对混合车流下中小跨桥车载效应极值计算的适用性,但是缺乏对长加载长度情况的讨论。Zhou等[9]提出组合广义帕累托分布法(combined generalized pareto distribution,CGPD),结合理论算例和实际车辆荷载效应对比不同的极值分布参数估计方法对结果准确性的影响,但研究仅与传统超阈值方法进行了比较。周军勇等[10-11]通过具有理论解的数值算例证明,两种组合极值方法均能很好地适应多事件混合影响下的车辆荷载效应极值推定,并且相比于传统方法误差更小,但其未针对极值推定影响因素等方面进行深入探讨。
综上研究,目前国内外相关研究尚缺少对考虑加载长度影响的组合极值方法适用范围的讨论。本文针对组合极值方法在大跨径桥梁中的应用问题进行研究,首先对组合广义极值法和组合广义帕累托方法进行回顾,对其理论基础和应用到大跨径桥梁时的核心问题进行讨论。以某悬索桥为例,计算得到不同加载长度下两种组合方法的极值推定结果,考虑影响结果准确性的主要因素,并基于理论探究和结果比较分析两种方法的适用性。
1 研究背景
1.1 组合极值推定方法回顾
组合广义极值法和组合广义帕累托方法是两种基本的组合极值推定方法,“组合”体现在:对于某一荷载效应样本Xi,可认为其由k个加载事件组成,其中k=1,2,...,nt,nt表示最多的可能加载事件数量。所有加载事件作用下效应样本Xi不超过某一分位值s的概率P[Xi≤s]可根据全概率公式计算如下:
式中:Fk(·)表示第k个加载事件效应样本的累积分布函数,ϕk为第k个事件在总体中所占的比重。
两种组合方法均要求所划分的加载事件相互独立且满足同分布假定,但方法针对的样本及其拟合分布存在差异。CGEV 方法以效应的区间最大值Ŝ为样本,以经典极值理论[11]为基础,组合分布模型依赖于各事件对应的广义极值分布Gk(s)。而CGPD方法以大于某一固定大值u的效应超出量X̂为样本,以超阈值理论为基础,组合分布模型依赖于各事件对应的广义帕累托分布Hk(x)。式(2)~式(3)分别为Gk(s)、Hk(x)的表达式。式中:s和x分别为区间最大值样本Ŝ、超出量样本X̂对应的某一分位值;u为样本阈值;μk、σk、ξk依次为位置参数、比例参数和形状参数,由第k个加载事件对应的样本拟合确定。
考虑到直接运用式(1)计算所有事件作用下的样本组合概率分布较繁琐,部分学者结合不同样本及其分布特性提出简化的组合概率方法。Caprani等[8]将CGEV方法中组合最大值分布模型的计算简化为式(4),前提是要满足样本符合极值分布或者区间内样本数足够大的充要条件。Zhou等[10]将CGPD方法中组合超出量分布模型的计算简化为式(5),但要求阈值足够大表示。
通过上述分析可知,两种方法在应用时均有其适用条件。CGEV 方法对样本数的要求,本质上是对底分布拟合误差的限制。加载事件单独作用下样本分布的拟合误差会传递至组合分布模型中,因此有必要检验荷载效应样本,要求各加载事件下的样本服从单峰分布且具有一定拟合优度。CGPD方法对阈值选取有一定要求,较高的阈值能够保证样本独立性,但样本量减少使拟合误差增大;较低的阈值虽然保证参数估计的稳定性,但样本独立性降低,同样会导致结果误差。因此,研究阈值对外推极值的影响并选取合适的阈值,对CGPD 方法中极值的计算至关重要。
1.2 分析采用的车流特性
CGEV与CGPD方法中均要求所划分的加载事件相互独立,且各事件引起的荷载效应满足同分布假定。根据研究[10]:不同加载事件产生的荷载效应有很大差异,大跨径桥梁的加载事件可根据交通状态确定。
桥梁在某一时段内的交通流状态可分为正常交通和高峰交通,本文参考珠三角、长三角等国内8地实测WIM数据,基于车流、车辆信息统计,通过相关性分析与K均值聚类形成不同交通状态对应的车流参数体系。相关性分析可简化参数量,得到用于聚类的特征参数;交通样本聚类则为确定交通类型提供了可行的途径。具体过程如下所述:
(1)针对统计得到的流量系列参数、车重系列参数以及车速系列参数,通过计算相关系数分析变量间的线性相关性。分析得知:同系列参数的相关性高,不同系列之间的相关性低,因此每个系列至少各选一项作为特征参数。但经敏感性分析发现车速的影响较小,故以流量和车重作为聚类特征。
(2)根据相关性结果,同时考虑到车重应兼顾平均水平和峰值水平,本文最终选择流量、车重均值、车重0.95 分位值作为聚类特征。采用K均值方法将WIM数据聚为若干类,选取产生效应最不利的一类进行分析。统计相应的车流参数(如车重、车速分布等),并根据桥上实际情况确定正常和高峰状态的交通量。
(3)基于上述参数采用元胞自动机方法[3]生成各交通状态对应的随机车流。
两种交通状态下的车流统计特征见表1,表中的事件1对应正常状态车流,事件2对应高峰状态车流。两类车流具有相同的车重比例,车流时长均为21d。在相同时段内,高峰期的车辆荷载分布更加密集,其车流的平均密度和平均集度更大。随机车流的生成综合了多地实测数据以及桥梁自身交通量,并考虑到可能出现的正常和高峰两种实际交通状态,因此既能反映该桥交通特性,同时也具有代表性。

表1 不同交通状态下随机车流统计特征Tab.1 Statistical characteristics of random traffic flow in different traffic environments
1.3 分析采用的典型效应
为了进一步说明组合极值推定方法对不同加载长度效应的适用性,本文选择某悬索桥中两个加载长度差异较大的效应分别进行加载,效应影响线如图1 所示。其中,主缆轴力效应的影响线遍布全跨且较为平缓,在全加载区间内对荷载敏感,其加载长度为1 208m;跨中吊杆轴力效应的影响线具有突出的峰值,荷载只在构件临近区域内对构件效应有较大影响,其加载长度约为250m。
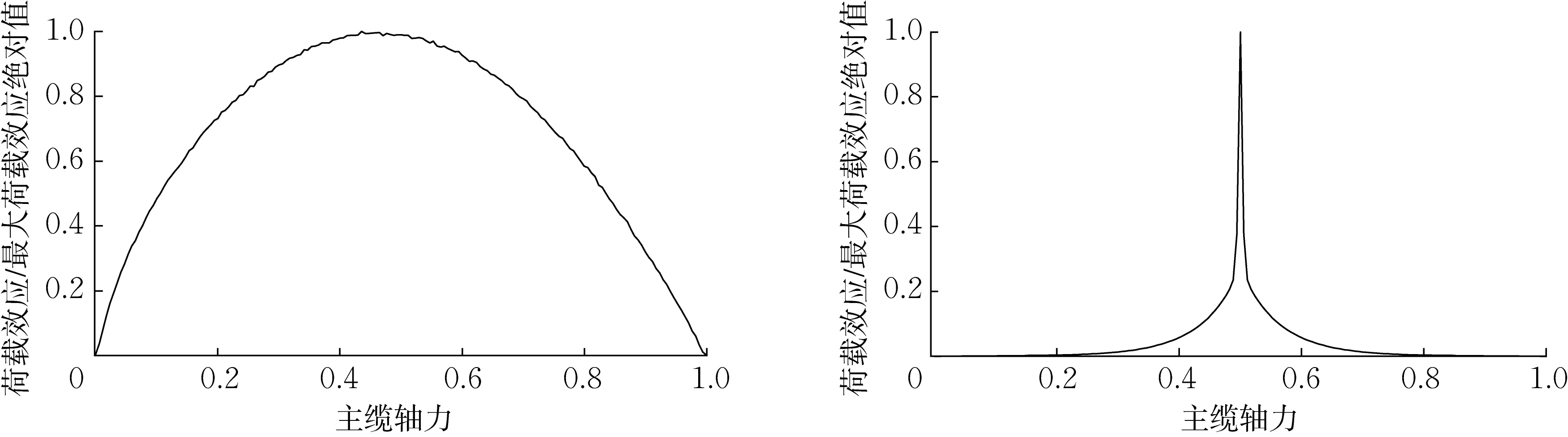
图1 不同加载长度荷载效应影响线Fig.1 Influence lines of load effect with different loading lengths
根据模拟的随机车流对影响线进行加载,生成车辆荷载效应。观察效应概率密度分布,如图2 所示。由图可知,主缆轴力效应和吊杆轴力效应均呈现多峰分布特征,不符合经典极值理论或超阈值理论假定,但各加载事件下的荷载效应满足单峰分布。可见,大跨径桥梁车辆荷载效应极值推定不适合用传统的极值外推方法,需要采用组合极值方法进行极值外推。
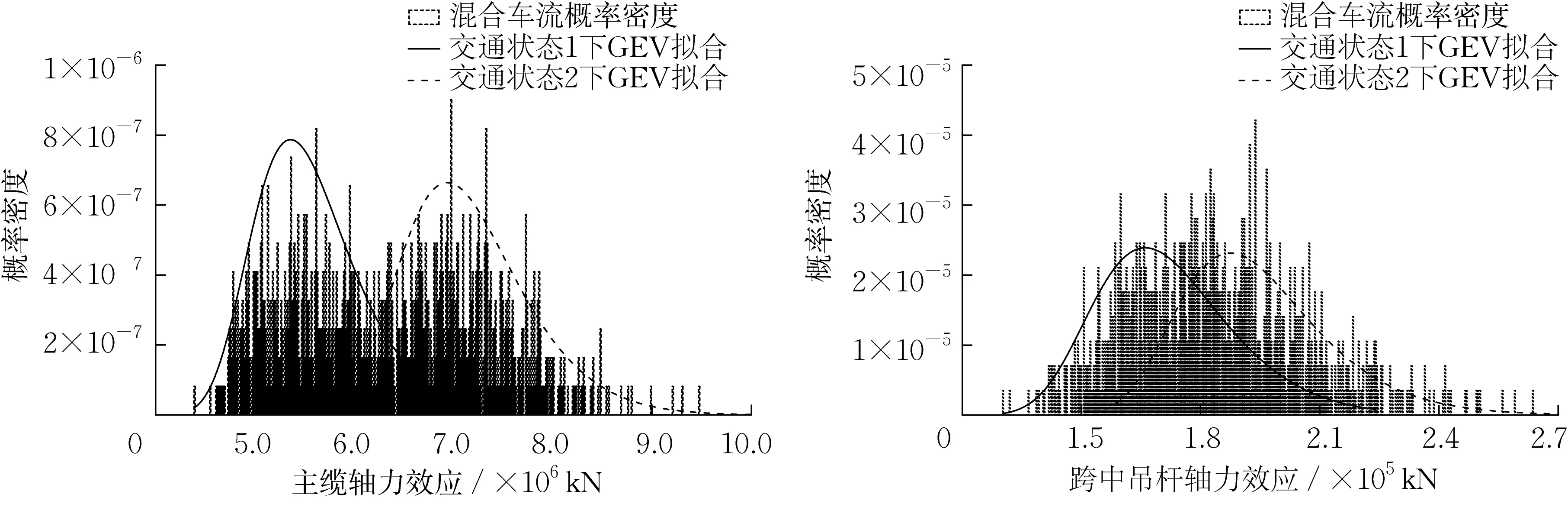
图2 车辆荷载效应概率密度图Fig.2 Probability density diagram of vehicle load effect
下面将以主缆轴力和吊杆轴力效应为例比较分析两种组合极值方法的外推结果和影响因素。
2 组合广义极值法适用性分析
2.1 充分样本量下的极值外推
首先采用CGEV方法进行充分样本量情况下的极值推定。以h 为区间长度单位,经检验:h 区间最大值样本满足独立性假定。采用广义极值(generalized extreme value,GEV)分布对样本数据进行拟合,其参数通过极大似然估计[12]计算。将所有加载事件k(k=1,2)对应的GEV参数ξk,σk,μk代入式(2)和式(4),获得多事件混合下的荷载效应最大值分布P[Ŝ≤s],由此即可外推任意给定评估周期下的效应极值公式如下:
式中:P—1(·)为混合事件下荷载效应最大值分布的反函数;T为荷载效应的重现期(单位为年)。
将各独立加载事件以及混合事件的拟合曲线、外推极值绘制于Gumbel概率纸,如图3所示。可以看出对于大跨径桥梁车辆荷载效应极值推定,经典极值理论的计算结果较CGEV方法小。将组合外推极值与各事件单独作用时的极值进行比较,发现如下规律:主缆轴力效应在各事件单独作用下的GEV拟合曲线没有交叉区域,其组合外推结果与事件2(高峰状态)单独作用下的结果相同,考虑多事件混合的主缆轴力效应极值直接由控制性事件2产生的效应决定。而吊杆轴力效应在各事件单独作用下的GEV拟合曲线之间可能存在相交,无法通过某一事件的GEV外推结果确定效应极值。
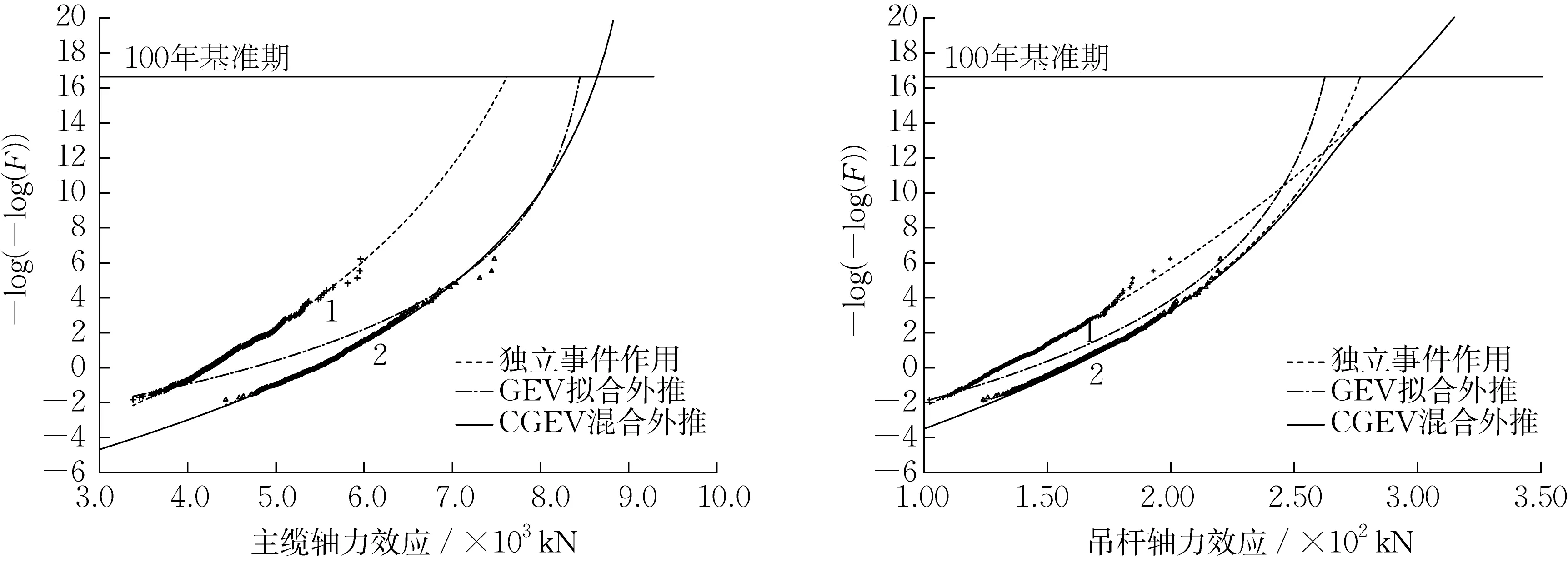
图3 小时区间最大值样本及其CGEV拟合外推Fig.3 Hourly maximal load effects and their CGEV models fitting on individual and mixed traffic flow
2.2 有限样本量下的极值外推
为了进一步分析CGEV方法的适用范围,对最大值样本量进行调整。以日为区间长度单位,经检验:日区间最大值样本同样满足独立性假定。与小时区间相比,日区间最大值样本的样本量显著减少。为了能更直观的观察样本量对极值结果的影响,分别下调2和4个样本量作为两组样本对照。仍采用GEV分布对样本数据进行拟合,通过极大似然估计[12]计算参数ξk,σk,μk并代入式(2)和式(4),根据得到的组合最大值分布即可外推任意给定评估周期下的效应极值。
将各独立加载事件以及混合事件的拟合曲线、外推极值绘制于Gumbel概率纸,如图4所示。当以d为区间长度单位时,通过CGEV方法计算的主缆轴力极值与小时区间的外推极值有差异。此时样本量的微小变动会立即引起各加载事件下GEV分布拟合结果的较大波动,甚至产生对控制性加载事件的误导,体现出CGEV方法在有限样本量下的局限性。
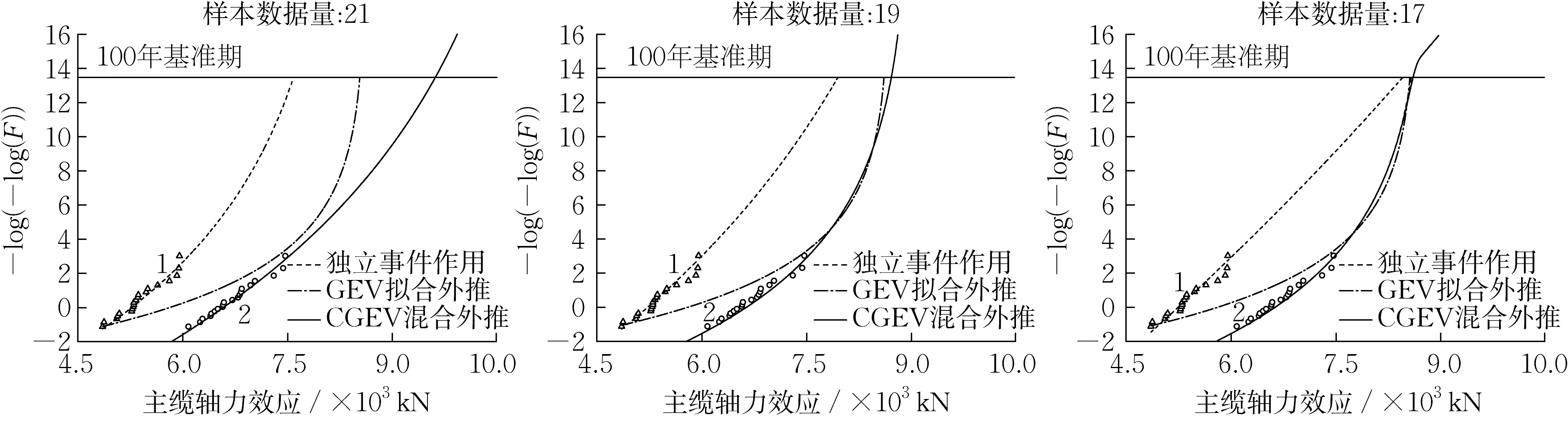
图4 不同样本量的日区间最大值样本及其CGEV拟合外推Fig.4 Daily Maximal load effects and their CGEV models fitting under individual and mixed traffic flow
2.3 样本量与底分布影响分析
以上采用CGEV方法对不同样本量的效应样本进行极值推定,下面将从底分布的角度对样本量变化引起极值结果变动的原因进行分析验证。图5为各事件作用下不同样本量对应的主缆轴力效应底分布及其拟合,表2列出了相应的均方误差与CGEV外推结果。
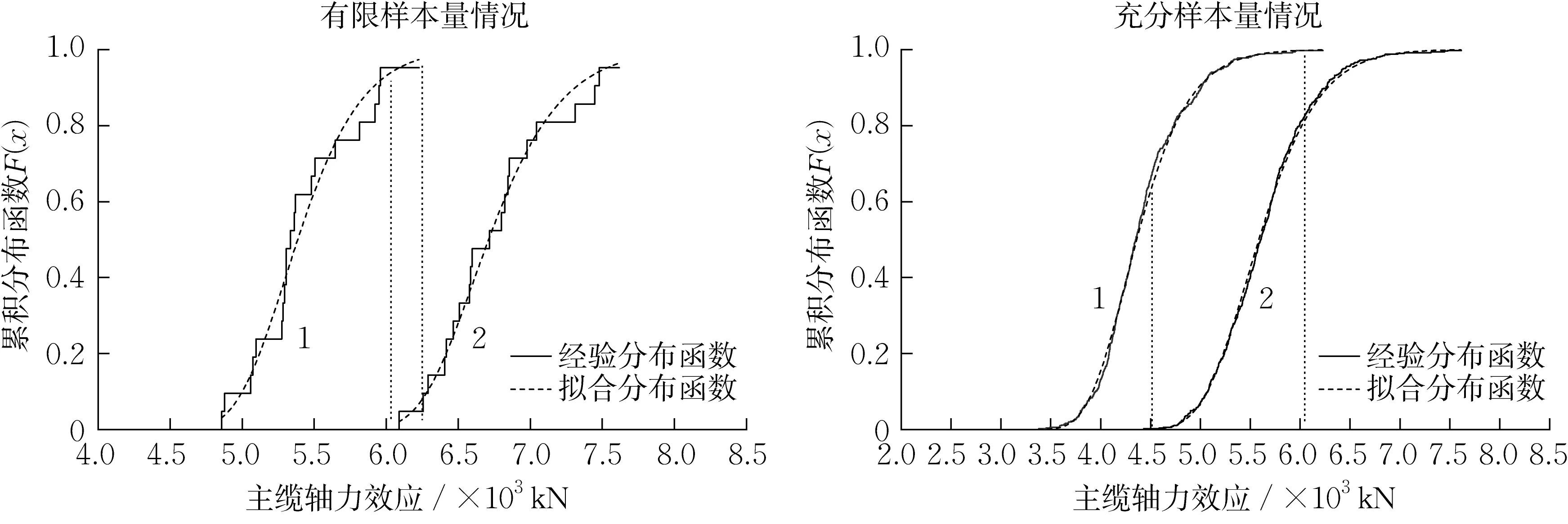
图5 不同区间最大值样本底分布及拟合Fig.5 Bottom distribution and simulation of maximum samples in different blocks

表2 不同样本量下的均方误差与极值比较Tab.2 Simulation fitness and comparison of CGEV extrapolation results in different sample sizes
由表2数据可知,样本量减少会明显增大底分布的拟合误差。结合图5可分析造成这种差异的原因:在最大值样本有限的情况下,底分布数据较零散,无法采用一种极值分布来描述数据的特征。考虑到CGEV方法本质上不会改变极值特性,所以当用式(2)组合各效应分布时,组合最大值分布仍会保留各事件底分布的拟合误差,影响极值推定结果的准确性。
结合式(2)对不同加载长度效应组合外推结果产生差异的原因进行分析,组合广义极值方法中组合最大值分布模型是单独加载事件下累积分布函数的乘积。累积分布函数具有单调递增性,且区间范围为[0,1]。只有在任意事件下累计分布函数值均处于区间(0,1)时,才能同时考虑到不同事件的影响。图5 中这个重合段即为两条虚线之间的区域。区域范围越宽,CGEV 极值外推时不同事件单独作用下拟合曲线相交的概率就越高。反之,区域范围越窄,甚至区域不存在时,CGEV极值外推的结果将由其中的控制性事件所决定。
3 组合广义帕累托法适用性分析
3.1 较高阈值下的极值外推
首先采用CGPD方法进行较高阈值情况下的极值推定。由于不同加载事件下的阈值存在差异,在CGPD法中以各独立加载事件阈值的最大值为其共同的阈值u。采用GPD 分布对样本超出量进行拟合,其参数通过概率权重矩法[13]计算。将所有加载事件k(k=1,2)对应的概率ϕk和GPD 参数ξk,σk,u代入式(3)和式(5),获得多事件混合下的样本超出量分布P[X̂≤x],由此即可外推任意给定评估周期下的效应极值,表达如下:
式中:P—1(·)为混合事件下样本超出量分布的反函数;nd为车辆荷载效应时程的天数;nPOT为超阈值样本总量;u为样本阈值。
将各独立加载事件以及混合事件的拟合曲线、外推极值绘制于Gumbel概率纸,如图6所示。对于大跨径桥梁的效应极值推定,CGPD 法外推结果与传统超阈值理论计算极值存在一定偏差,但其与充分样本量下的CGEV外推极值相似。
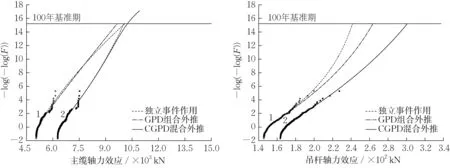
图6 较高阈值下的样本及其CGPD拟合外推Fig.6 Samples with high threshold and their CGPD models fitting on individual and mixed traffic flow
3.2 较低阈值下的极值外推
为进一步分析CGPD 方法的适用范围,基于KS检验方法对阈值进行调整。K-S检验通过比较拟合结果与实际结果的最极端差分值D与检验标准Ds,判断分布函数拟合值与样本真值的近似程度。当两者误差达到最小,即满足|Ds-D|=min时,拟合值与真值最接近。D、Ds的表达式为
式中:Hk为超出量样本所属的帕累托分布;F为给定分布;n为样本数量;α为置信度。
图7 为事件1 作用下主缆轴力和跨中吊杆轴力效应拟合的K-S检验结果。当D曲线与Ds曲线相交时,拟合累积分布函数曲线与实际的车辆荷载效应经验累积分布之间的误差最小,此时参数估计的稳定性最优。
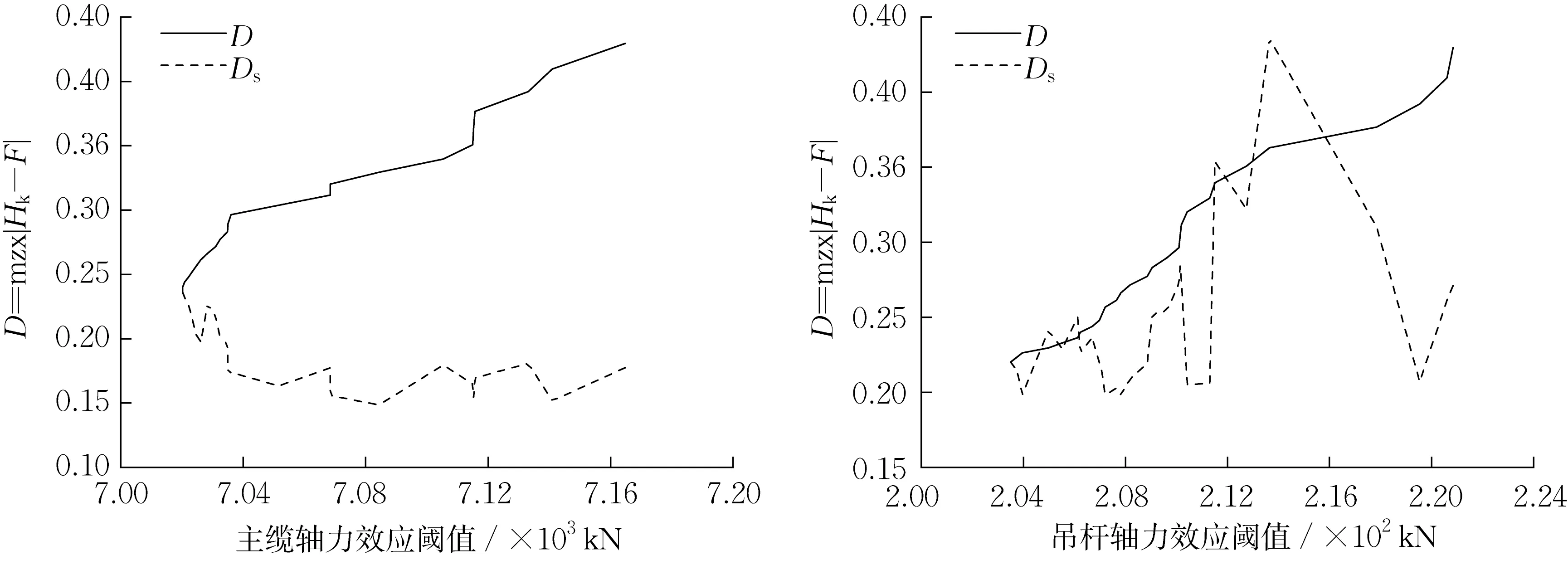
图7 不同阈值超出量样本的K-S检验Fig.7 K-S test of different threshold samples
将各独立加载事件以及混合事件的拟合曲线、外推极值绘制于Gumbel概率纸,如图8所示。
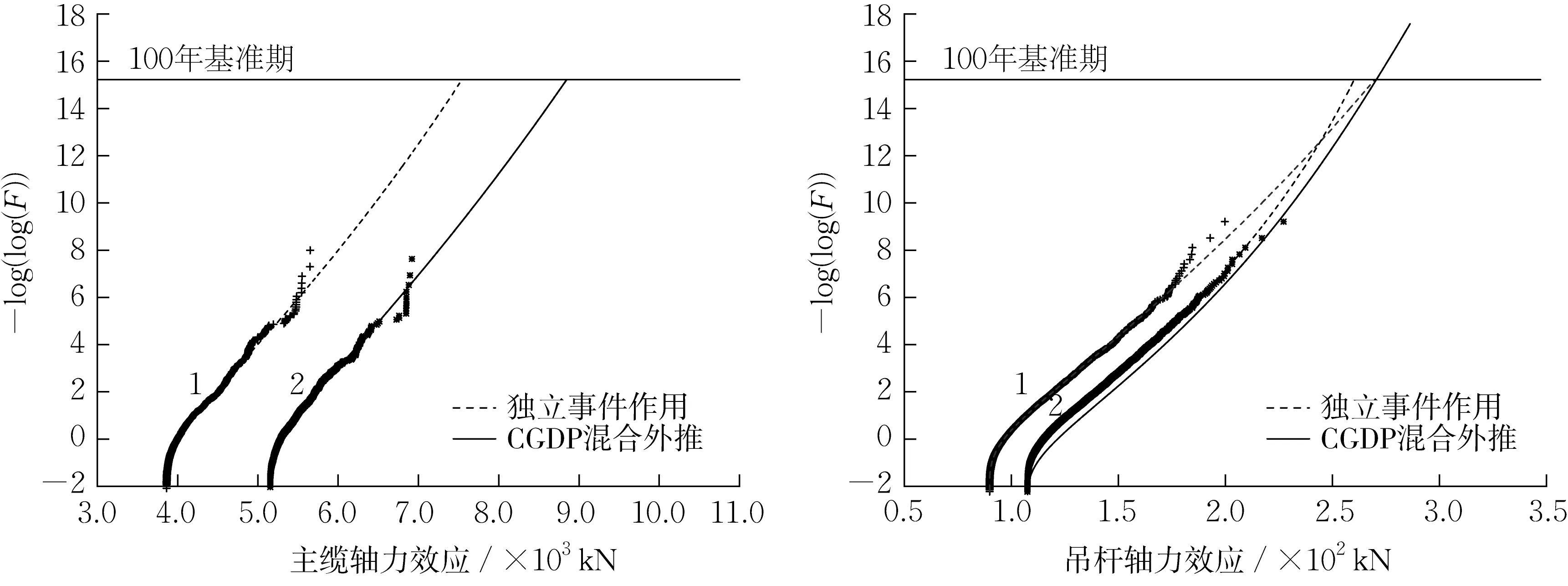
图8 较低阈值下的样本及其CGPD拟合外推Fig.8 Samples with low threshold and their CGPD models fitting on individual and mixed traffic flow
对比图6和图8可以看出,不同阈值下通过CGPD方法计算的主缆轴力效应极值仅存在约5%的偏差,吊杆轴力效应极值存在约10%的偏差。综合分析图8和图3发现,当面对不同加载长度的荷载效应时,CGPD方法存在与CGEV方法相似的规律。
3.3 阈值影响分析
根据第1节中的分析,在选取超阈值样本时,过高的阈值会减少样本量,使拟合的准确性下降;而过低的阈值虽然保证了参数估计的稳定性,但样本的独立性无法满足。以上分别对较高阈值以及阈值选取使样本满足最佳稳定性两种情况下的效应极值进行了计算,对其结果(见表3)进行比较。

表3 不同阈值对应样本的CGPD外推结果比较Tab.3 Comparison of CGPD extrapolation results of samples with different thresholds
随着阈值上移,超阈值样本量大幅减小,|Ds-D|值显著增大,但CGPD 方法的外推极值变化幅度仍限制在10%范围内。因此,可推测CGPD方法对由阈值选取引起的样本量变化敏感性小,适用于有限样本量下的极值外推。
4 比较与讨论
采用CGEV和CGPD两种组合极值方法推定大跨径桥梁中主缆轴力效应和吊杆轴力效应极值,与传统极值理论计算的极值相比较,结果列于表4。
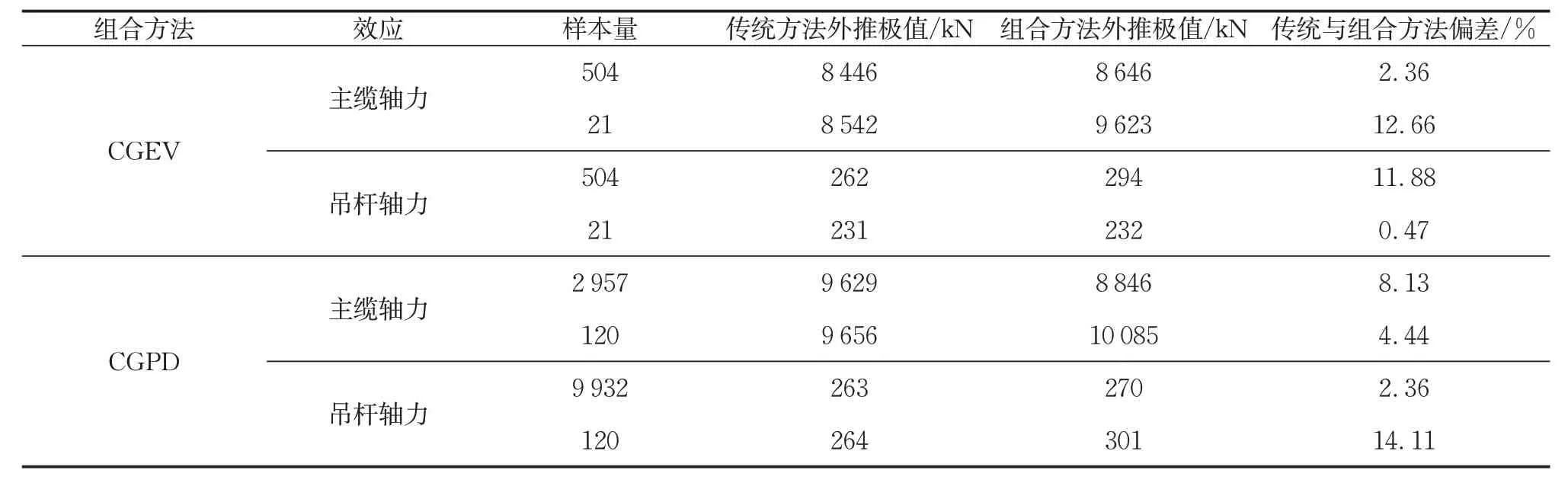
表4 组合极值方法与传统极值方法结果比较Tab.4 Comparison between combined extreme value method and traditional extreme value method
对于大跨径桥梁,采用不同的传统极值推定方法计算极值,其结果具有较大差异;采用两种组合极值方法计算极值,在充分样本量情况下的极值推定结果一致。这说明大跨径桥梁更适合用组合极值推定方法计算车辆荷载效应极值。当样本量大幅下降时,CGEV法的外推极值发生较大变化,而CGPD法的外推极值变化幅度基本小于10%,相对更为稳定。可认为,在有限样本量情况下适合采用CGPD 方法推定极值。
另一方面,根据前文分析归纳了以下规律:两种组合极值推定方法在面对充分样本量的长加载长度效应时,各事件单独作用下的分布拟合曲线一般不存在交叉区域,其组合外推结果直接由控制性事件(高峰状态车流)产生的效应决定。图9通过主跨分别为700m和1 490m的悬索桥案例证明该规律对于不同大跨径桥梁具有同样的适用性。
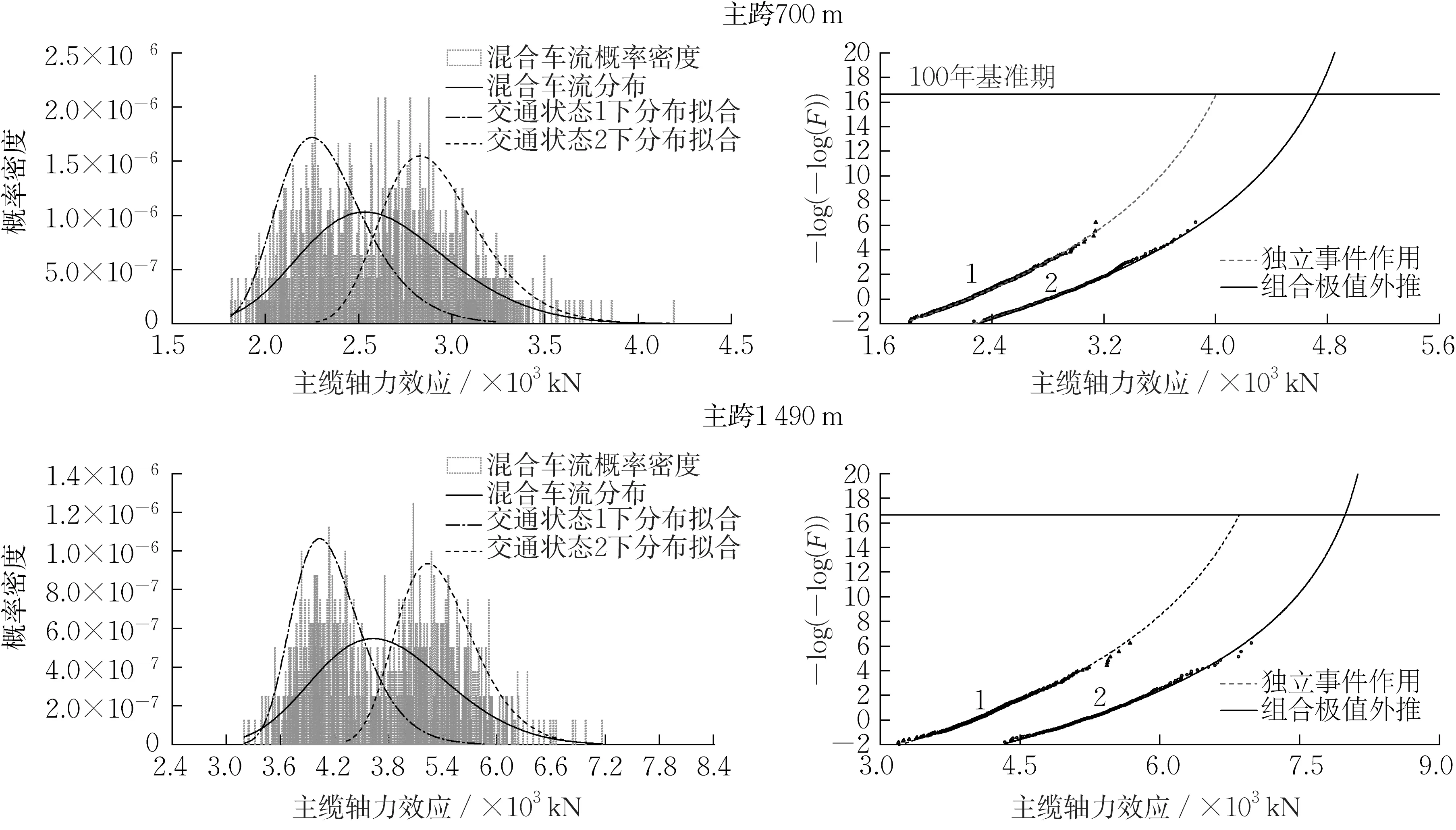
图9 不同跨径悬索桥主缆轴力和效应外推Fig.9 Extrapolation of axial force effect of main cable of suspension bridges with different span
5 结论
本文对目前桥梁汽车荷载效应的组合极值外推方法进行了综述,介绍了组合广义极值法和组合广义帕累托方法在大跨径桥梁不同加载长度效应极值推定中的应用,并对影响外推结果的样本量、底分布和阈值等关键参数以及方法适用范围进行了分析。论文主要得到以下结论:
(1)传统极值方法在大跨径桥梁效应极值分析中具有明显局限性,大跨径桥梁应采用组合极值推定方法计算车辆荷载效应极值。
(2)样本量对CGEV 计算结果的影响本质上是对底分布拟合误差的反映。当样本量较少时,底分布数据较零散,无法采用一种极值分布来描述数据的特征,故外推的极值准确性差。在CGPD方法中,随着阈值的上移,超阈值样本量大幅减小,|Ds-D|值显著增大,但CGPD 法的外推极值变化幅度在10%范围内,计算结果更为稳定。
(3)在有限样本量情况下,推荐采用CGPD方法外推效应极值。在充分样本量情况下,CGEV 法与CGPD 法的外推极值基本一致,但CGPD 方法在阈值选取方面较复杂,故推荐采用CGEV方法。
(4)长加载长度效应的极值推定具有规律性:当样本量充足时,长加载长度效应极值推定中各事件单独作用下的分布拟合曲线不存在交叉区域,其在多事件混合情况下的组合外推极值直接由控制性事件(高峰状态)产生的效应决定。
作者贡献声明:
阮欣:方法构思、模型设计、论文写作与修改;
赵鑫莹:模型推导、数据处理与分析,论文写作与修改;
金泽人:车流仿真,论文修改。
