基于DQN和K-means聚类算法的天然气站场仪表智能识别研究

黄知坤，文 炜，刘 明，张香怡，刘凯书，黄 腾，顾继俊

(1.国家管网集团川气东送天然气管道有限公司，武汉 430074；2.中国石油大学(北京)机械与储运工程学院，北京 102200)

0 引言

随着国内输油气管道与沿途站场规模的不断增长，利用机器人替代人工巡检成为当下研究重点。四足机器人具备高机动性与良好的越障能力，在油气站场巡检方面具有良好的应用前景。需要机器人根据现场环境变化与巡检指令进行自主多自由度组合控制，因此需要为机器人设计出顶层决策控制系统替代人工控制。

指针式仪表由于造价较低，结构简单，使用方便，结实耐用等原因[1]，大量存在于工业环境、生活环境、农业生产、医疗设备、国家航空等领域，在这些行业发挥着至关重要且基础的作用。是实时检测环境、检测数据、收集数据的一种好工具，具有非常广泛的应用场景。

目前，机器学习(ML)技术在大数据分析、图像识别、自动驾驶等人工智能领域表现出卓越的性能，使四足机器人的自主决策成为可能。深度强化学习(DRL)作为机器学习的重要分支，它既具备深度学习(DL)对复杂环境状态的拟合与刻画能力，又能够像强化学习(RL)一样对智能体施加动作决策，在一些控制领域其表现已经高于人类水平[2-4]。仪表读数识别算法得到了一定的发展，大多将机器视觉和人工智能结合起来，但是依旧有很多问题都没有被解决，因此导致了没有一套成熟的算法可以大规模的推广应用，只能在某些小规模、定制化的场景下使用，鲁棒性和普适性都不高。再者，油气田站场等室外环境的仪表自动读数会受光照条件、天气状况的影响，容易造成读数失败[5]。因此，需要研发出更加具有普适性的读表算法来解决这些问题。

本文针对天然气站场指针式仪表智能识别追踪，包括以下几个部分：仪表目标追踪、仪表定位、仪表配准、示数识别，流程见图1所示。

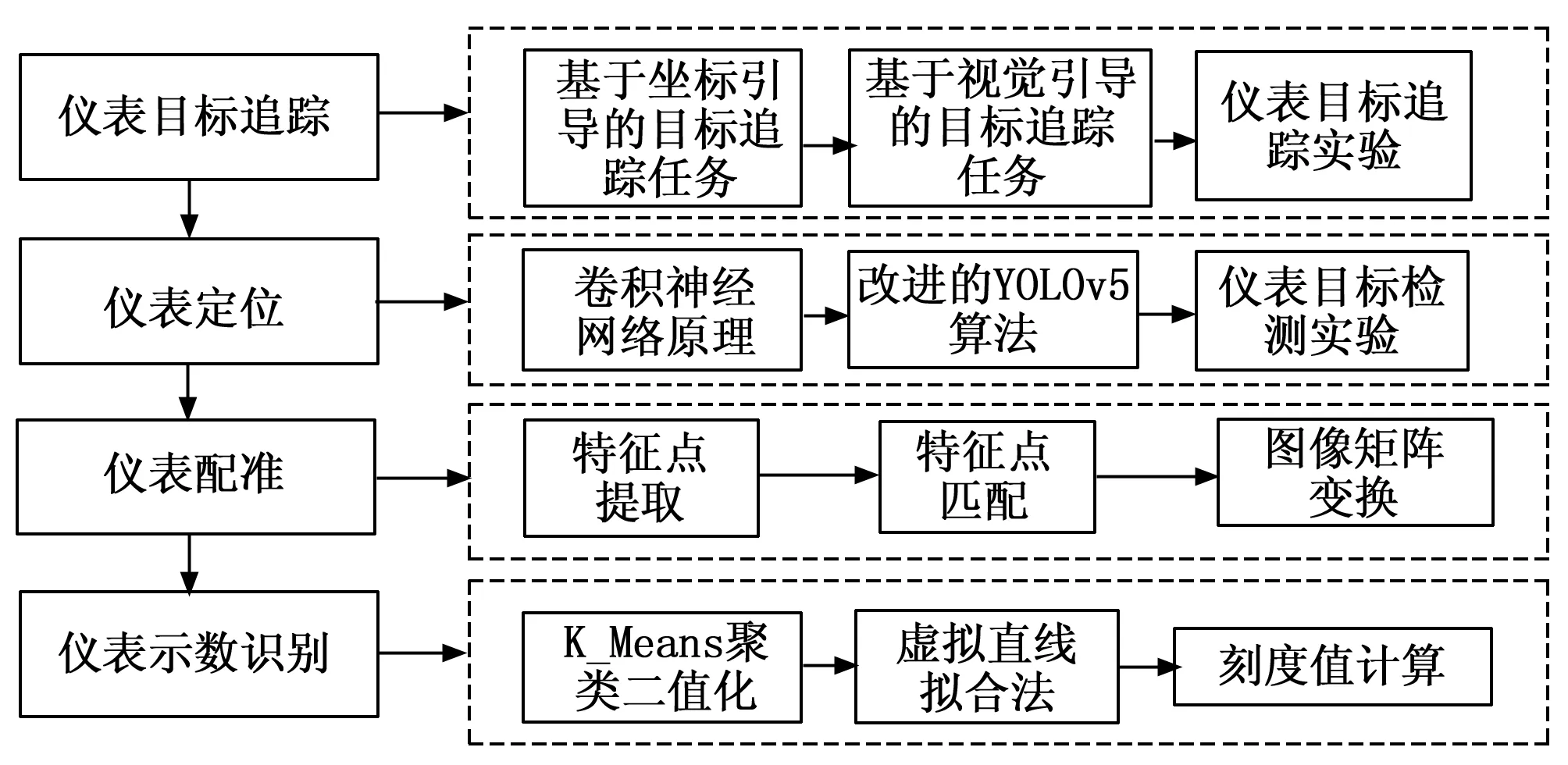
图1 仪表追踪及读数方法研究内容

本文在目标追踪方面，将采用DQN实现四足机器人在油气站场巡检进行仪表目标追踪仿真过程，通过基于坐标引导的目标追踪任务和基于视觉引导的目标追踪任务两种子任务，验证DQN在四足机器人运动控制上的性能表现，以达到仪表目标追踪的结果。在仪表智能检测方面，采用基于改进的YOLOv5算法，在卷积神经网络的基础上，自制仪表样本数据集并训练模型文件、优化权重文件；再通过YOLOv5算法识别四足机器人定点采集的图像中的仪表，并标出仪表位置。在角度调整方面，采用了基于改进的SIFT的图像配准算法，得到高质量的利于仪表示数读取的图像。在仪表示数读取方面，利用K_means聚类的二值化算法得到指针信息突出的表盘，并通过角度与仪表盘示数的关系，得到仪表示数。

1 基于深度强化学习的机器人单任务运动控制

为解决巡检过程中仪表目标实时追踪，本文提出了基于DQN模型的目标追踪算法，可实现定位系统、机器人视觉与运动控制融为一体。首先通过将仪表目标追踪任务分为基于坐标引导的目标追踪和基于视觉引导的目标追踪两个子任务，其次在第一个子任务中，通过四足机器人本身、传感器仪表目标的定位及DQN模型，实现目标的粗追踪。受定位传感器测量精度影响，子任务一难以达到规定精度，因此在第二个子任务中，设定机器人足端保持静止，通过视觉引导，控制机身做上下俯仰和左右扭转做高精度目标追踪。

1.1 基于坐标引导的目标追踪任务

四足机器人头部安装深度相机，可控制自身旋转速度使位于正前方4米处的管道仪表进入视野，如图2所示。任务中，仿真环境反馈机器人机身和目标仪表的三维坐标，与机器人机身欧拉角，同类型参数在现实环境可通过UWB定位系统和IMU测得。

1.1.1 模型搭建

该任务的环境参量为机器人与仪表空间坐标、机器人机身倾角，动作参量为两个正负相反数值相同的角加速度，此外，累加每轮动作执行的角加速度可间接得到机器人角速度作为环境参量的补充。由此可见，环境空间参量均为连续变量，即环境空间连续，而动作空间为离散参量，可以根据状态查表方式选择当前状态下价值最高的动作，传统Q学习算法无法解决连续状态空间问题，因此针对该任务选择DQN算法作为训练模型。训练模型如图3所示

图3 DQN算法模型

深度Q网络(DQN)是在Q学习算法基础上增加神经网络的学习方法，利用神经网络可以较好地处理连续状态空间问题。图中，环境对应仿真环境，经验池用以存储训练过程中采集的状态、动作、奖励和更新后的状态，目标网络与在线网络组成DQN模型中的深度神经网络部分，损失函数用以计算实际价值与预测价值的误差并更新神经网络参数。至于参数，s与s，为机器人状态向量，a为机器人所执行动作，r为状态s时刻机器人采取动作a所获得的实际回报，Q(s，a；θ)表示参数为θ的神经网络预测动作a的价值。

状态向量s包含9个元素，其形式如下：

(1)

式(1)中前3个元素为机器人机身坐标，中间3个元素为目标仪表坐标，最后3个元素分别表示机器人在Pitch轴和Roll轴倾角以及机器人围绕水平面旋转的目标速度，最后一组元素描述机器人机身稳定性，由于机身旋转速度过快会造成摔倒，故将累加产生的目标速度也作为状态参量。同时由于目标位置固定，为防止训练过程动作的选取依赖世界坐标系，故Yaw轴转角不计入状态参量。

1.1.2 训练测试与结果分析

任务训练在Pybullet仿真环境进行，将DQN训练程序与机器人控制程序分为两个线程进行。线程将每次任务训练从开始至结束定义为一回合，期间累加选择动作的次数作为机器人运动时间衡量，每轮回合结束分为3种情况：

1)机器人通过运动满足完成条件，任务成功；

2)机器人运动中途摔倒，任务失败；

3)机器人运动次数超过上限将视为超时。

另外，训练次数等于DQN模型更新次数，当训练次数超过规定上限立即保存参数模型结束训练。任务执行过程回放如图4所示。

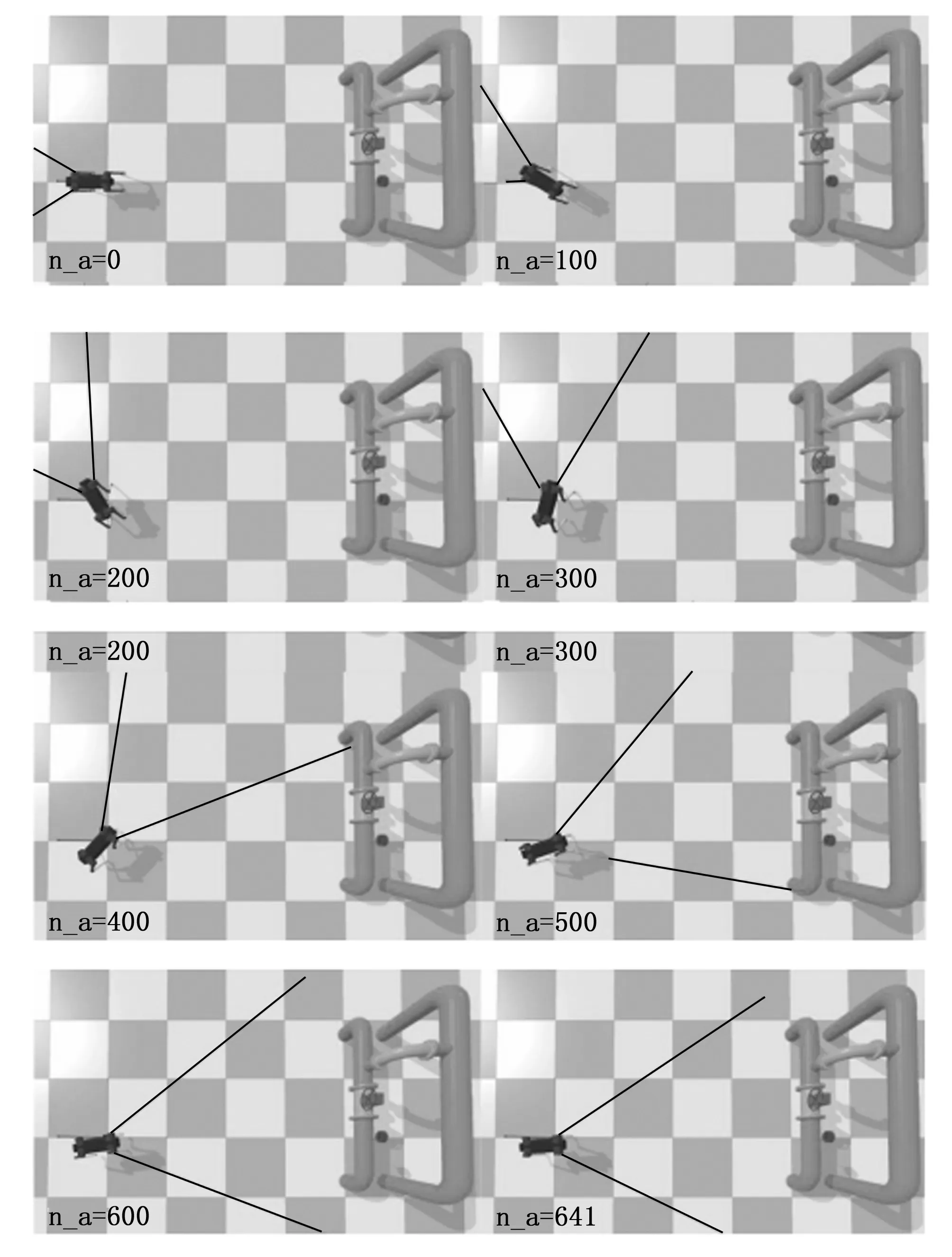
图4 DQN任务执行过程回放

DQN模型初始化参数设置如下：最大训练次数10 000，学习率0.01，折扣因子0.9，贪心因子0.9，神经网络复制间隔500周期。同时，每隔1 000次训练记录模型损失并保存保存该时刻模型参数，结果如图5所示。可见随着训练进行模型损失曲折下降，损失逐渐收敛趋势，训练前期模型损失下降较快，当训练至第6 000轮时模型损失达到最小，而后损失稍有上升并小幅波动。

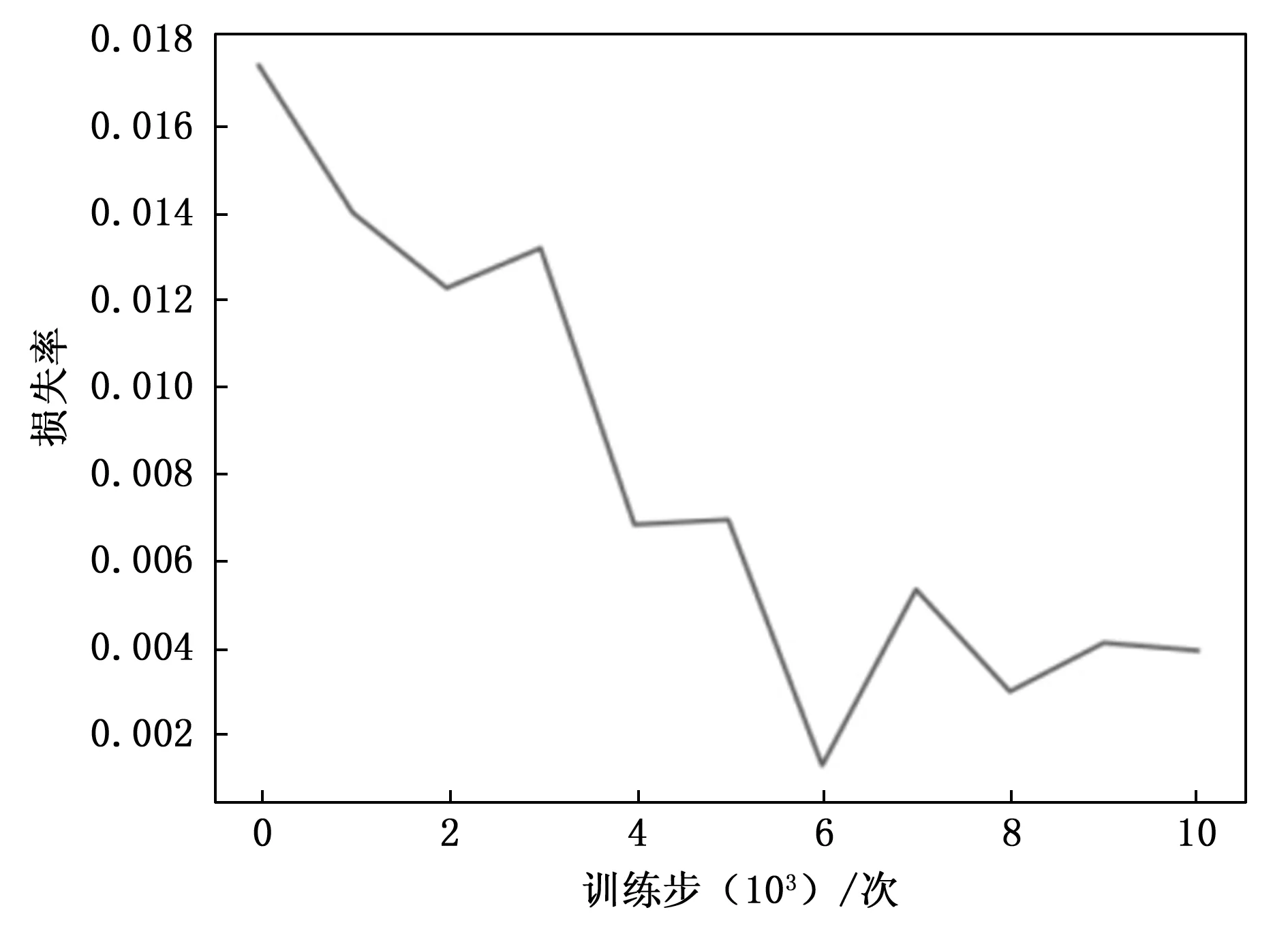
图5 损失函数曲线图

1.2 基于视觉引导的目标追踪任务

第二个子任务主要在第一个子任务基础上进行，设定机器人通过自身旋转运动已经将仪表纳入摄像机视野，同时机器人与目标仪表的距离也进入了摄像头的视距范围，此时需要将仪表.影响移动至摄像机画面中央(图6)，以便后续读取仪表示数。

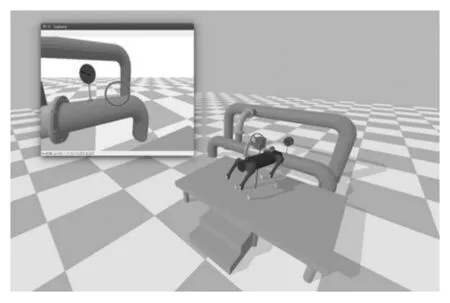
图6 任务仿真环境

本任务的环境状态s将不再包括位置坐标，取而代之的是机载相机的视觉画面，这要求机器人能够“看懂”画面内容并引导自身朝向目标方向调整姿态。同时，为防止目标位姿超出机器人活动空间，也需将目标位姿作为极限位置参考加入环境观测量。机器人方面，实现机器人在全运动空间内的位姿调整。

对于模型的搭建大体上与前节任务相同，根据任务内容变化做如下调整：环境状态定义如下：

s=[Mphoto，θt_p，θt_y]

(2)

式(2)中Mphoto为摄像机单帧图片矩阵，原图为640×480的三通道彩色图片，为降低神经网络权重数量提高训练速度同时便于经验存储，将原图转换为单通道灰度图片，并将原二维像素矩阵压缩重构至长度为48×64的一维向量。θt_p和θt_y是机器人在Pitch和Yaw旋转轴上的目标角度。

本任务的状态观测量为二维矩阵与一维向量的组合形式，考虑到需处理图片数据，网络模型主体应包含卷积神经网络(CNN)，同时需对网络模型进行调整以兼容一维状态参数。受InceptionV3模型启发，建立并联式强化学习在线/目标网络模型如图7所示。

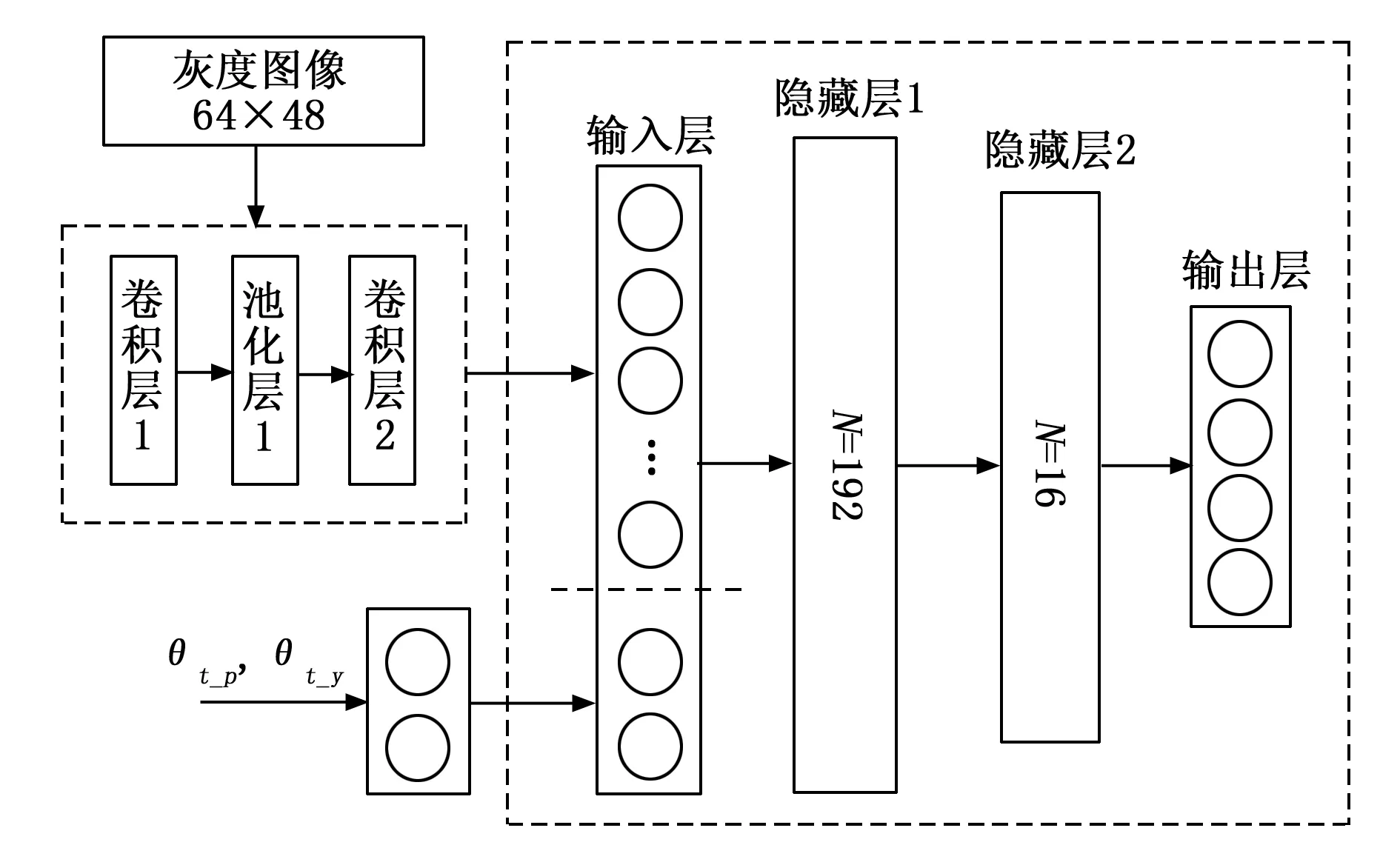
图7 改进后DQN的深度网络部分模型

该模型首先对输入的灰度图像做卷积、池化处理减少网络节点数量，而后设置四层全连接神经网络，将卷积处理产生的一维图像参数与一维位置参数拼接合并作为全连接网络的输入层，最终通过正向传播输出4种动作的概率分布。在全连接层部分，隐藏层之间采用Relu函数做非线性激活，隐藏层至输出层采用Softmax函数激活确保所有输出动作概率和为1。

1.2.1 训练测试与结果分析

DQN模型初始化参数设置如下：最大训练次数10 000，学习率0.06，折扣因子0.9，贪心因子0.9，神经网络复制间隔50周期。每回合训练开始时，机器人Yaw轴角度随机设置在正负30°的区间内，保证表盘完整出现在相机视野中。同时，每隔1 000次训练记录模型损失并保存保存该时刻模型参数，结果如图8所示。与任务一的训练结果相似，前1 000轮训练过程模型快速收敛，之后模型损失趋于稳定并伴随小幅波动，当训练结束即训练至第10 000轮时，模型损失降至最低。任务执行过程回放如图9所示。

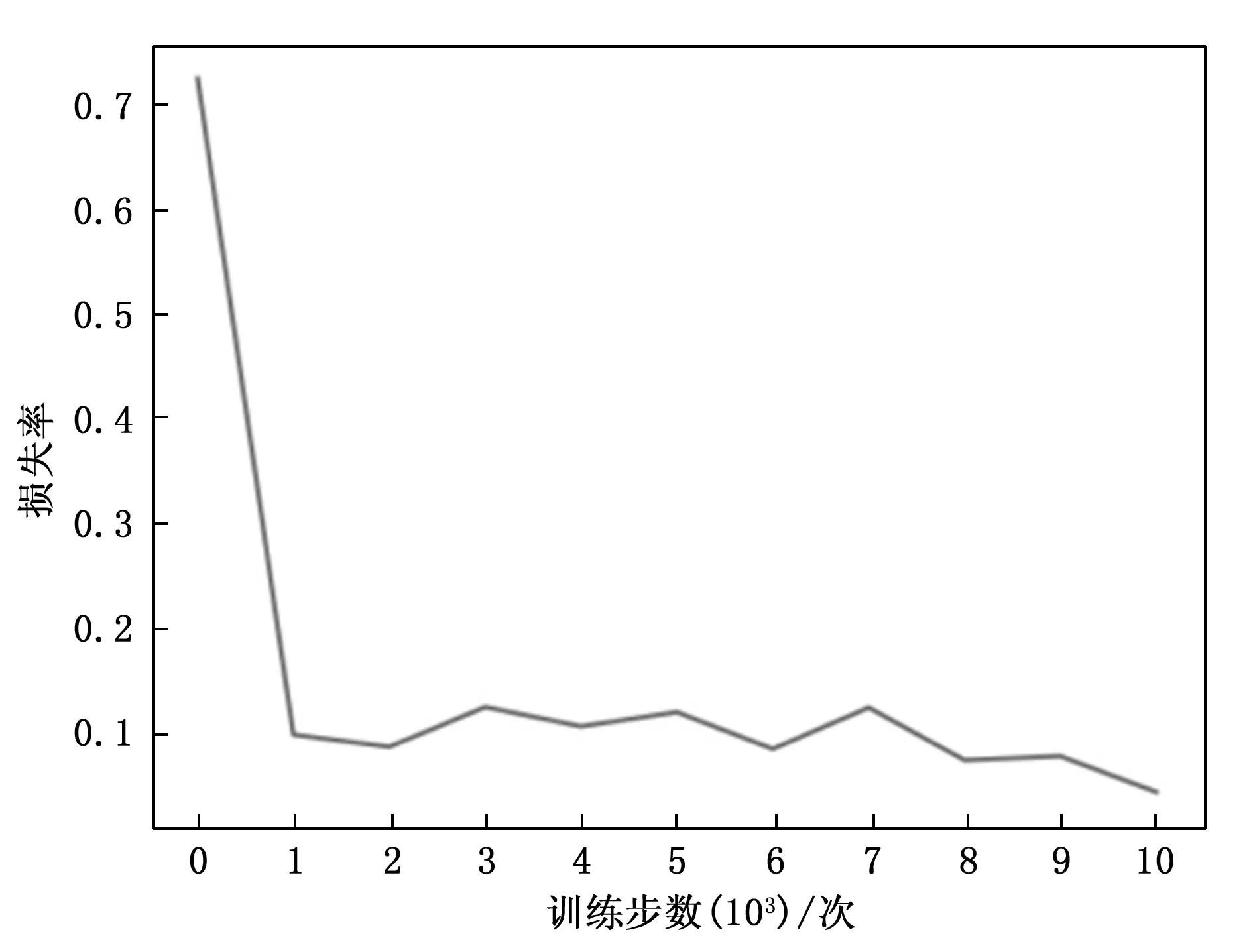
图8 损失函数曲线图

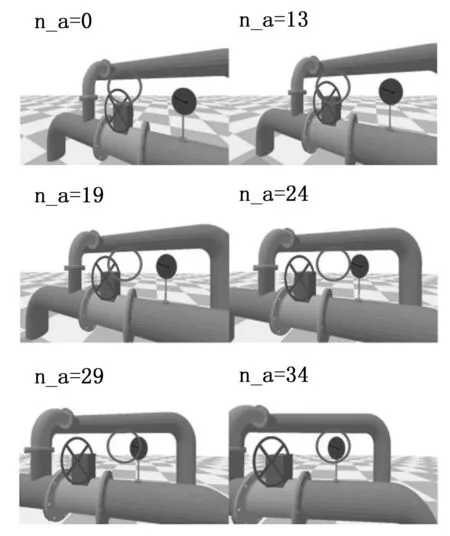
图9 任务执行过程回放

通过两个子任务证明，采用DQN算法能够将机器人视觉与运动控制融为一体，机器人能够根据任务奖励条件对输入图片进行自主分析处理，形成稳定的动作策略，人员通过调整奖励条件即可指导机器人学习，无需涉足图片分析过程，便可达到对仪表的目标追踪。

2 指针仪表定位及配准

本文采用卷积神经网络算法作为仪表定位的基础，由于基于深度学习的卷积神经网络的基础是大量的数据。本文利用COCO数据集进行数据处理，该数据集包含了生活当中常用的大部分物体的样本集以及对应的标注集。根据2018年的数据[6]，目前公开的数据当中并不能够找到有关仪表的训练样本集，因此，从天然气站场实地拍摄了大量的仪表图像作为基础，并完成图像的标注和反复迭代的训练任务，生成识别所需要的数据样本集。

在样本数据集的基础上，使用YOLOv5算法进行仪表识别，识别效果见图10。

图10 仪表识别效果图

由图10可以看出，识别效果较好，仪表识别出来的置信度较高。

摄像头在固定位置检测到仪表模块后，需要将检测到的仪表模块修正为模板视角。只有经过修正的图像才能够继续进行下一步示数的读取，否则很容易因为图像拍摄角度等原因造成采集到的仪表存在倾斜问题，造成读数存在误差。因此本文针对仪表倾斜问题使用改进的SIFT算法进行仪表图像的修正运算。修正步骤如图11所示。

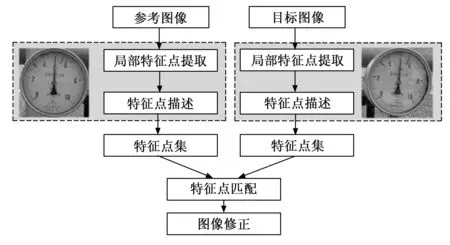
图11 仪表配准步骤

3 指针仪表示数识别

由于指针式仪表都需要读取指针，对于直线检测的研究从未间断。目前识别指针的方法主要有Hough算法[7]及其改进算法、Bresenham[8]算法、最小二乘法等。Hough变换可以读到边界，但是仪表识别过程中线条并不单一，难以分类，且并不能够读到仪表指针的长度。Bresenham算法和最小二乘法都无法过滤噪声，在考虑光照环境和外界天气条件时，处理结果并不理想。

本文提出了一种新的仪表示数读数方法，该方法对计算机的要求较低，不需要深度学习网络，只需要简单的算法就可以进行仪表的识别，识别流程见图12。

图12 仪表示数识别流程图

针对修正后的图像，需要对表盘进行处理后再读取指针，由于天然气站场环境复杂，背景杂乱，直接对图像进行简单的二值化处理后进行读数会加大计算的难度。本文通过K-means聚类并保留内切圆的方法对图像进行二值化处理，得到表盘清晰的图像后，用虚拟直线拟合法添加一根过中点的直线，旋转360度得到与指针重合度最高的角度，从而得到指针的角度，最终得到指针指向的刻度。

3.1 图像二值化

图像二值化是指给彩色的图像设置阈值，大于阈值的所有像素点的灰度值都设置为255(白色)，小于阈值的所有像素点的灰度值都设置为0(黑色)，将整个图像变为黑白图像[9]。可以使图像的数据量大幅度减少，减少运算的负担。

为了突出仪表中的主要因素，例如：刻度、数字、圆心、表盘等。本文针对机器人识别的两幅仪表图像做二值化处理，中值分别取80和127。针对图13中的1图和2图分别作不同参数的二值化处理，见图13。

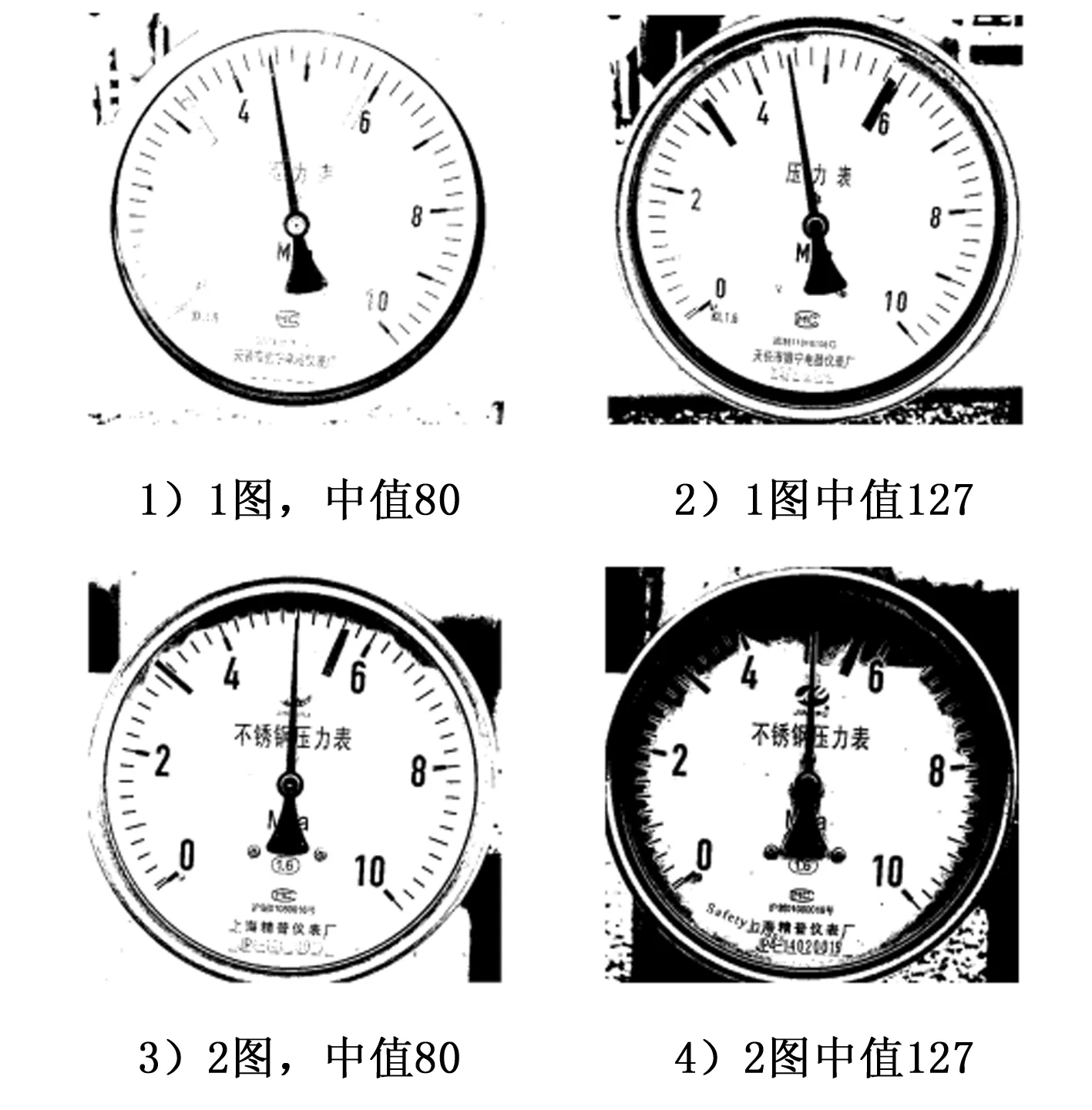
图13 不同中值的二值化效果

中值80是指将灰度值大于80的部分设定为白色，灰度值小于80的部分设定为黑色；中值127是指将灰度值大于127的部分设定为白色，灰度值小于127的部分设定为黑色[10]；将图像调整为只有黑白的效果。

针对光线较强的1图，中值为80时表盘信息较弱，有可能丢失重要信息；中值为127时，表盘信息较为清晰，可用作后续处理。

针对光线较暗的2图，中值为80时表盘清晰，可以用作后续处理，但是中值为127时，表盘黑色部分较多，有可能丢失重要信息。

若在程序中人为的设定中值，在不同的光线条件下，处理效果不同，可能会导致结果的偏差。

3.2 K-means聚类二值化

分为了使图像二值化的更加智能，使其无论在怎样的背景下都能有好的处理效果，本文采用K-means聚类二值化来处理图像。

K-means算法是一种基于距离的聚类方法，评价不同像素点的相似性的评价指标是距离。距离越近的对象，说明其相似度越大[11-14]。各个像素点数据事先并没有类别之分，该方法的核心思想是通过迭代寻找m个类簇，得到这m个类簇的灰度值的均值来代表各自的样本，使得各个样本的误差和达到最小。也就是各聚类点的灰度值本身要尽可能的紧凑，而各聚类之间要尽可能的远离[15-18]。

该算法的基础是每个类别的每一个参数与该类别的均值做差的平方和加上其他所有类的平方和的总和要达到最小。即最小误差平方和准则。

(3)

式中，μc(i)表示第i个聚类的均值。

各类别的样本越相似，与该类别的均值间的误差平方和越小。当平方和达到最小时，就认为聚类为最优解。

算法流程图如图14所示。

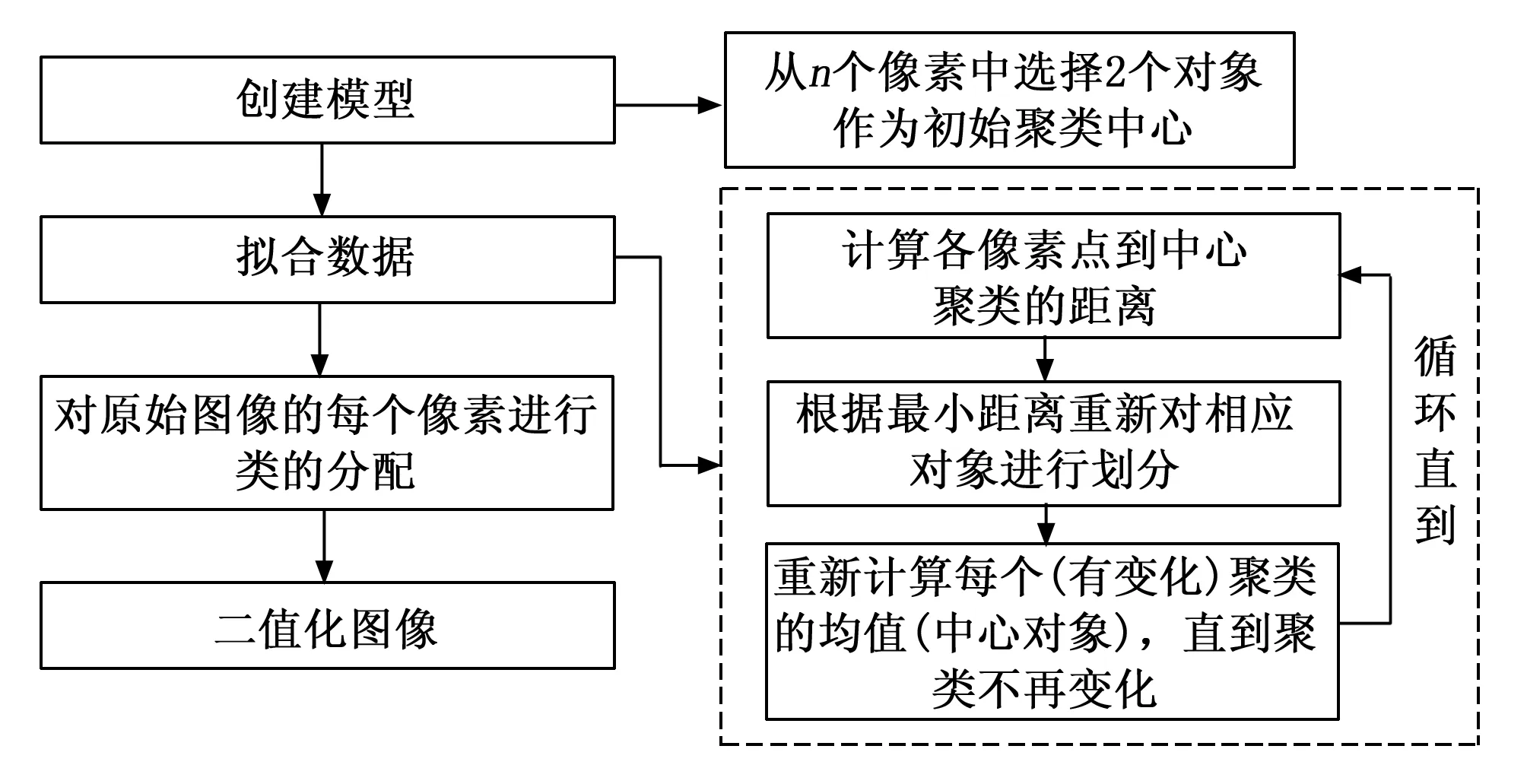
图14 K-means二值化算法流程图

由于图像是由RGB三个通道的图像组成，所以图像被分为两个类簇后，得到的聚类中心为2×3的矩阵。第一类簇偏向白色；第二类簇偏向黑色。

聚类方法[19-20]使得图像迭代多次后自动筛选出白色的类簇和黑色的类簇，如图15所示。

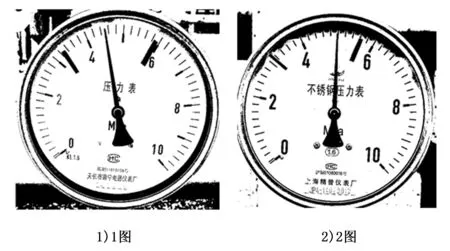
图15 k-means二值化效果图

不论是图15中的1图还是2图，图像的二值化效果都不错，可以大大提高仪表识别的精度，降低图像数据量，提高识别速度。

由于重要的信息如均在表盘上，为了进一步简化数据量，采用内切圆算法，将表盘以外的所有像素点清除，流程图如图16所示。

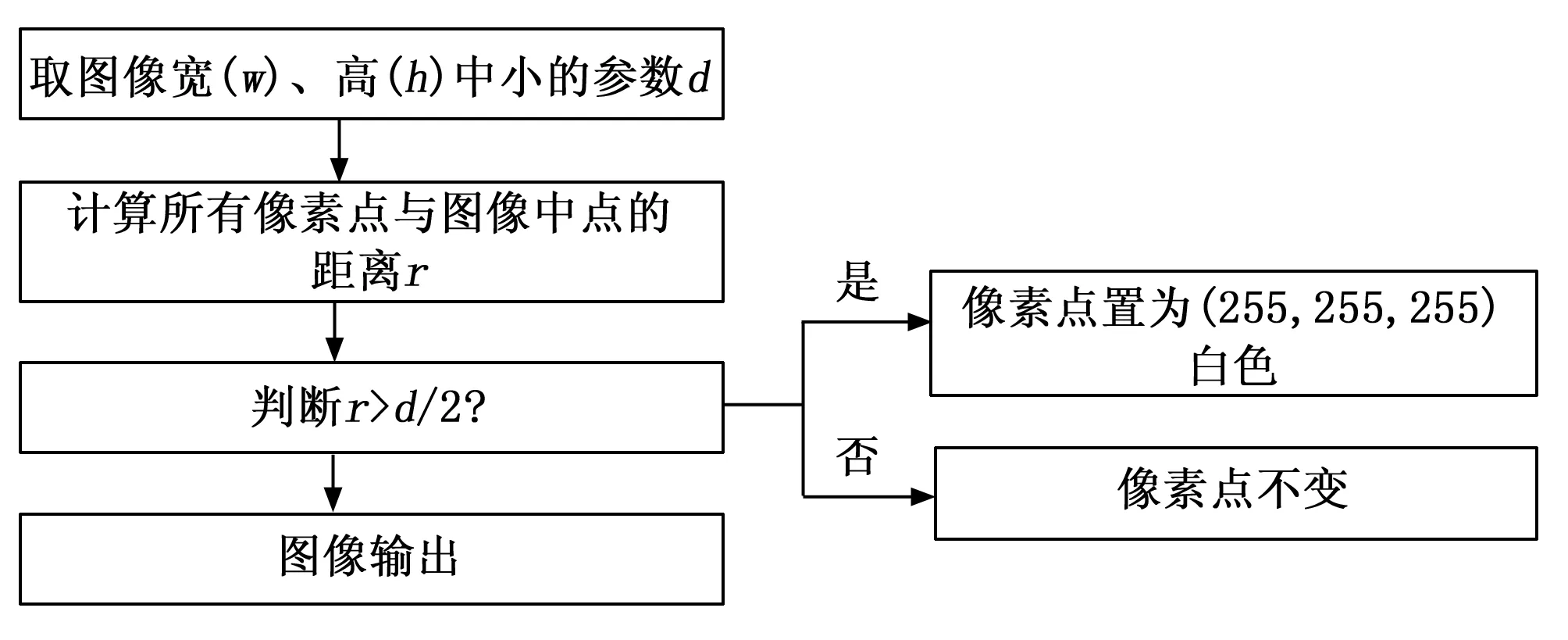
图16 内切圆算法流程图

要得到图像的内切圆，首先需要将图像较短的一条边记为d，再遍历图像中所有的像素点与图像中点的距离r，比较d/2与r的长度，如果r较大，说明该像素点处在表盘之外，置为白色即可；如果r较小，说明该像素点处在表盘之内，则不必更改该像素点灰度值。该算法得到的图像数据量小，且重要信息都得到了有效的保留，去除背景信息，使其应对复杂背景也拥有一定的鲁棒性，为后续的处理提供了重要保障。

经过内切圆算法处理的效果如图17所示。

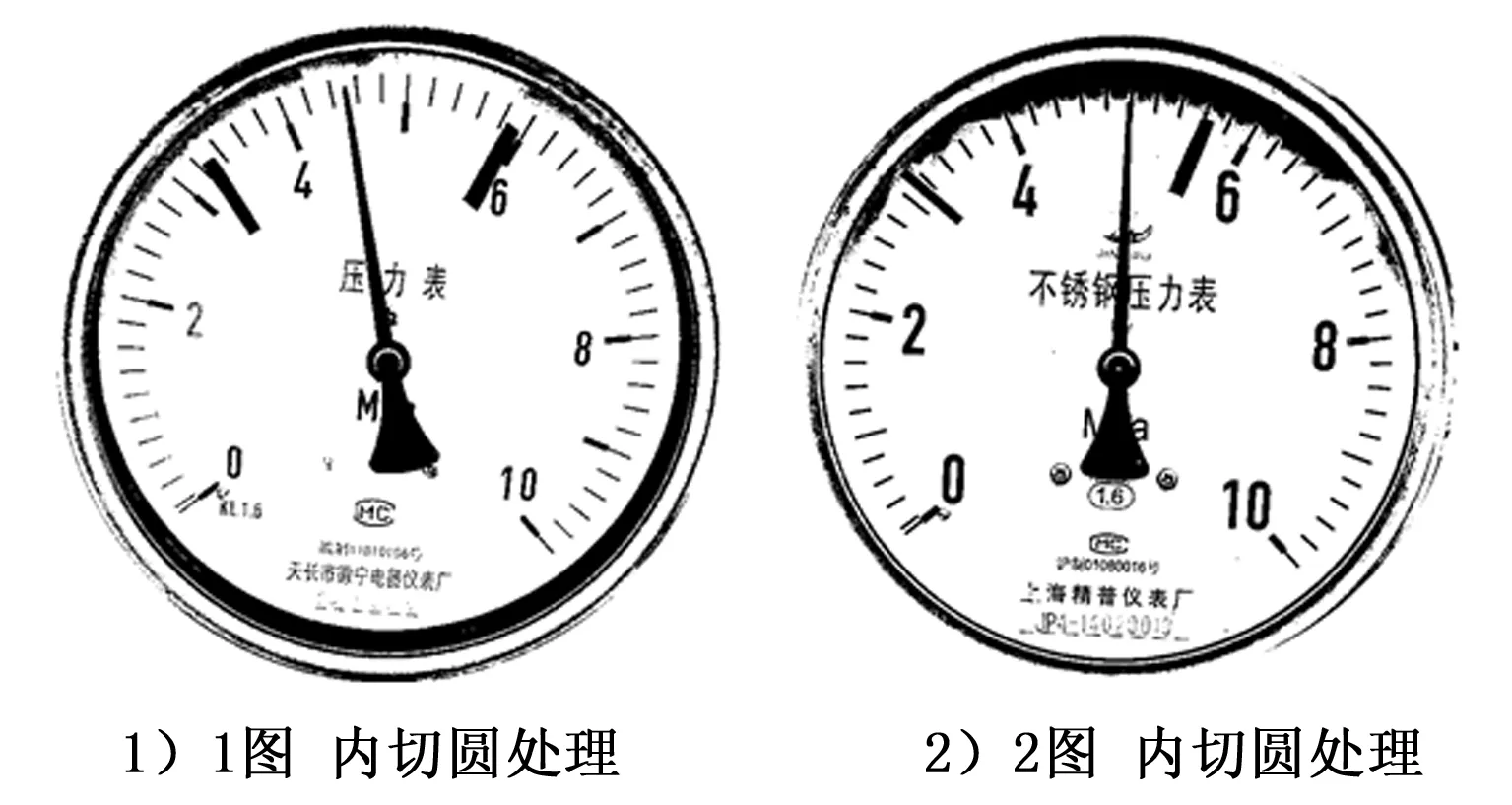
图17 内切圆仪表效果图

内切圆算法使得图像重要信息得到保留的基础上，降低了数据量。

3.3 虚拟直线拟合法

在识别仪表的过程中，最重要的一步是要识别指针的角度，在通过角度换算得到仪表的示数。

本文采用旋转的虚拟直线拟合法，添加一条直线从图像中点指向表盘刻度，直线从右边的0度位置顺时针绕着图像中点旋转，见下图。

图18中的红色直线为虚拟直线，该直线通过表盘中点，长度设为表盘半径的十分之九，由零度位置旋转360度。

图18 虚拟直线旋转360度

图19为直线零度位置示意图，红色直线旋转过程中精确计算直线与表盘指针的重合度，图20反映了红线在旋转过程中与图18的表盘中的黑色像素点重合的数量。重合度最高的点所对应的角度数就是表盘指针的角度。

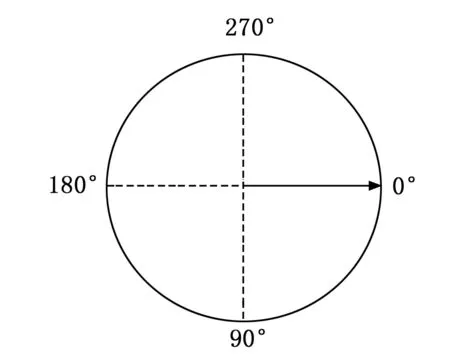
图19 度数示意图

图20 直线与表盘黑色像素点重合数量

通过观察上图可以发现重合度在270°左右达到最高点，93°左右是次高点，符合仪表状态，最高点是指针指向的度数，次高点是指针后端指向的度数。此时程序认为270°即为仪表指向的角度。

3.4 计算刻度值

取得仪表指针指向的角度并不能够知道仪表指针的刻度值，需要进行相应的计算。本文选择将度数与特殊刻度值一一对应，选定的刻度值有：0、1、2、3、4、5、6、7、8、9、10。选定圆心坐标为(121，116)，半径为99，同时需要得到0刻度对应的角度以及最大刻度对应的角度。

本文所用案例的0刻度对应的角度为135度，10刻度对应的角度为45度，0～10之间刻度均匀分布，可计算每一个刻度之间相隔度数°。0刻度和10刻度之间间隔90°，剩余度数为360°-90°=270°，那么每一个刻度之间的间隔度数为270°/10=27°。根据对应的角度，计算出X、Y坐标，对应的坐标计算结果如下表，刻度值用k表示，对应角度用v表示。由于9刻度和10刻度对应的角度跨过了0度线，所以需在在对应度数的基础上减去360度。具体对应关系见表1。

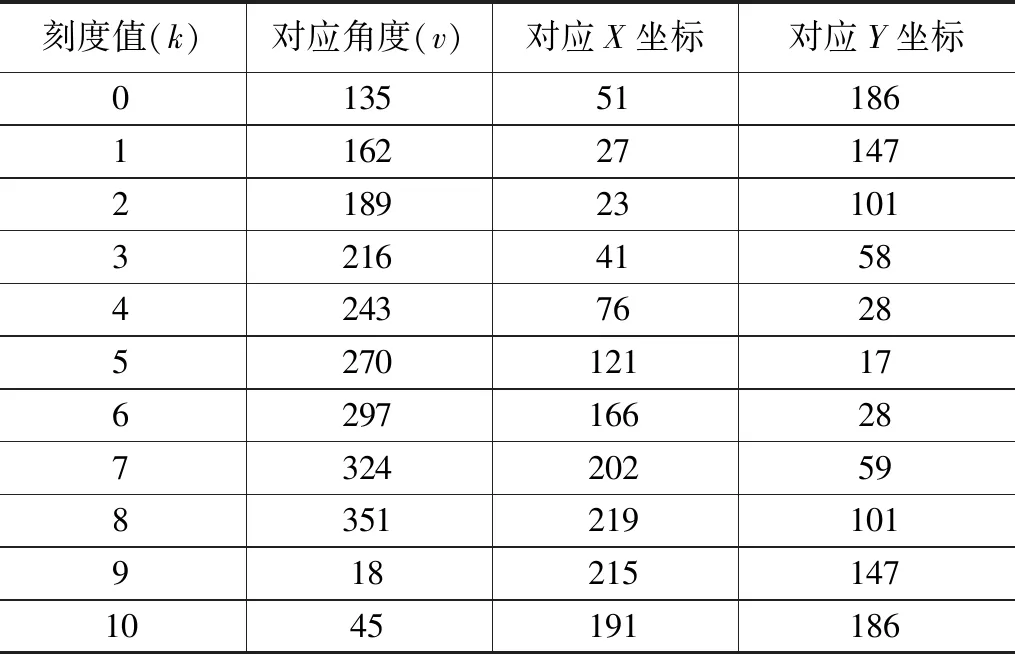
表1 刻度与角度对应关系

开始计算3.3节传回的仪表指向的角度r所对应的刻度值。

1)先计算传回的角度r对应刻度值的整数部分，定义整数部分为变量m。

刻度k[]与v[]存在一一对应的关系，定义函数result[k]=v。通过将r与上表中的对应角度v依次做对比，若r>v，则将m置为v对应的刻度值k，继续下一行比较，直到r<=v，跳出循环。此时的m为实际刻度的整数部分。

2)计算传回的角度r对应刻度值的小数部分，定义小数部分为变量t，小数部分所占角度为d，见图21。

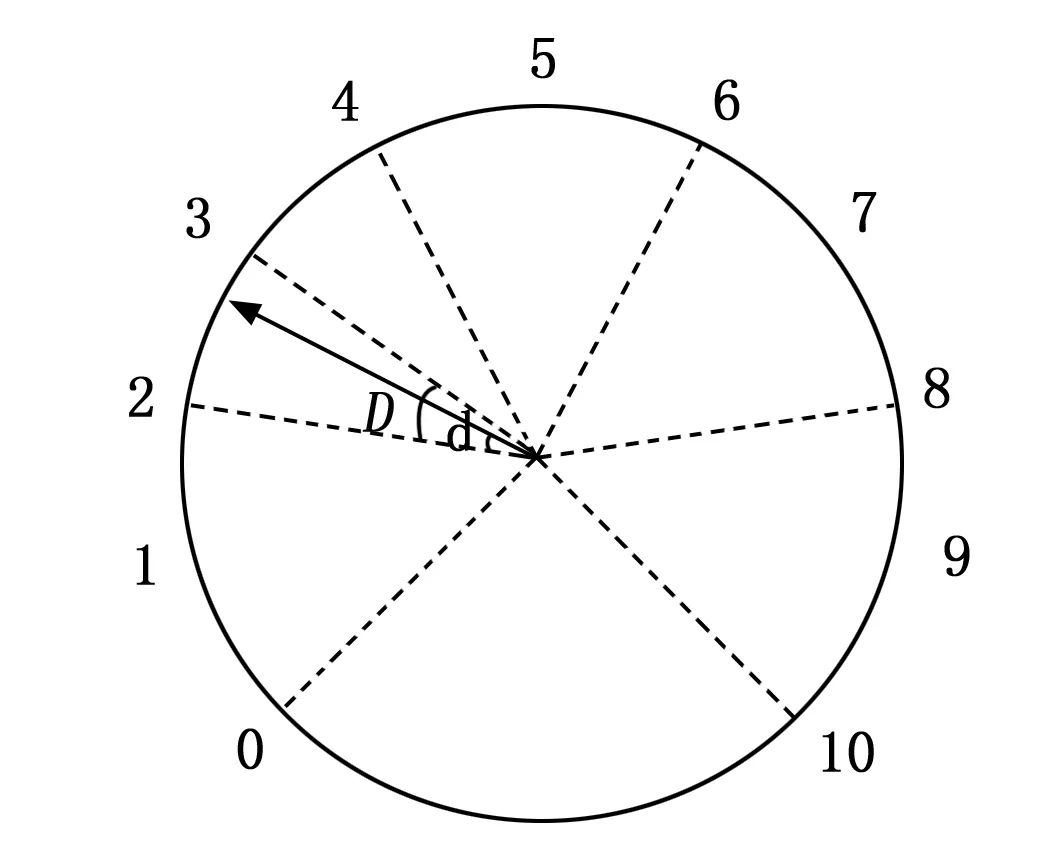
图21 小数部分刻度关系图示

可知，仪表盘中相邻两个数之间所占得小格子为10个，要得到小数部分，必须知道小数部分占了几个格子。

t=0.1×d/(D÷10)

(4)

D÷10为每个格子所占得角度，d/(D÷10)计算结果为小数部分占几个小格，一个小格为0.1。上式可以简化为

t=d/D

(5)

仪表的刻度总数P可用下式表示：

P=m+t

(6)

4 实验

4.1 实验硬件

本文使用的四足机器人巡检平台如图22所示，机器人机身内置1台惯性测量单元，头部面板处安装2台Intel Realsense深度摄像机，用于充当机器人的眼睛采集图像，在本文中重点采集待检测仪表的图像。

图22 巡检机器人巡检平台

图23 UWB定位系统

在室外的天然气站场真实环境，依靠UWB定位系统，提供给子任务一所需要的机器人及仪表所处的全局坐标，传感器精度可达到厘米级，误差小。

在室外的天然气站场，巡检机器人到达巡检的指定位置后，拍摄视野中的图像，并传到机器人的主控端进行识别。该巡检机器人上安装的摄像机为Intel Realsense深度相机，里面包含的摄像机参数如表2所示。

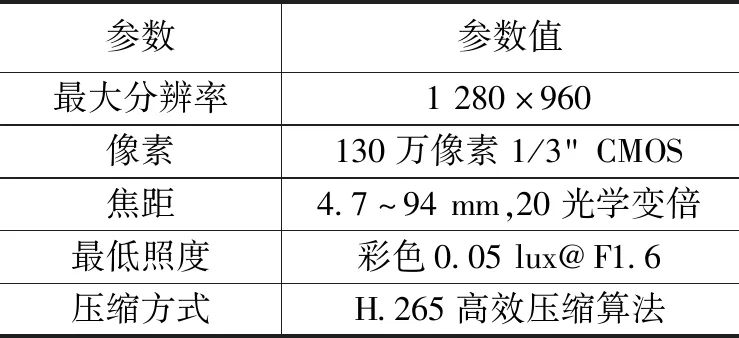
表2 摄像机参数

本次仪表检测的四足机器人环境为：Ubuntu操作系统，Python语言，OpenCV开源库。在Anaconda平台上开展深度学习的神经网络算法的训练，安装了CUDA运算平台，以Tensorflow作为深度学习算法框架。训练算法的实验硬件平台为：Intel(R)Core(TM)i7-9700 CPU @ 3.00 GH，8核16 G 内存，NVIDIA GeForce GTX 2070 GPU，4 G独立显存。

4.2 实验效果

本文按照子任务一和子任务二进行联合训练测试，运动过程如图所示，对四足机器人运动过程中训练轮数及平均执行动作数进行分析，结果见图24～25。

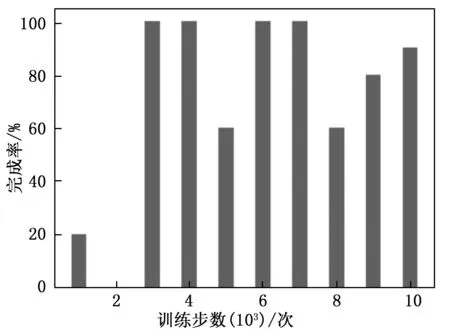
图24 任务完成率

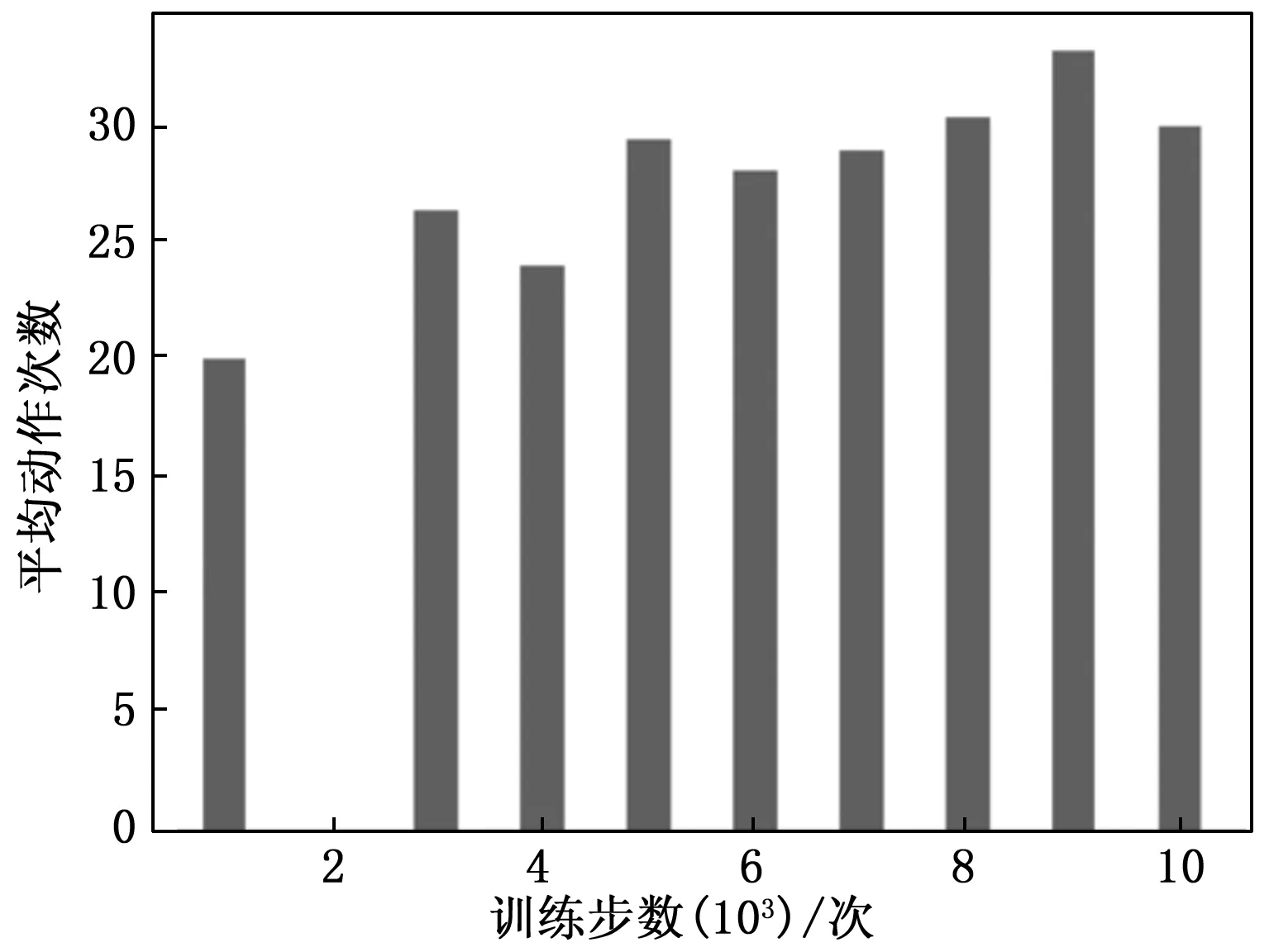
图25 平均动作次数

由图可知，前2 000轮训练内，机器人尚未完全“理解”任务规则，大部分回合因机身目标姿态超出运动空间而失败，仅有的成功是由于初始化时仪表恰处于画面中心位置，因此该阶段数据不具有参考性。随后的训练中机器人表现逐渐稳定，从第3 000轮至第7 000轮训练机器人基本能以百分之百的成功率将相机镜头对准仪表，并且平均执行动作数在25步到30步之间。

本文按照虚拟直线拟合法进行测试，在图像的左上角输出读到的指针参数，见图26。

图26 识别效果

由图26可以看出，在不同环境背景下，仪表识别的结果都与仪表实际的示数相近，本文使用了20张不同环境下的不同仪表图像进行仪表识别算法，识别结果如表3所示。

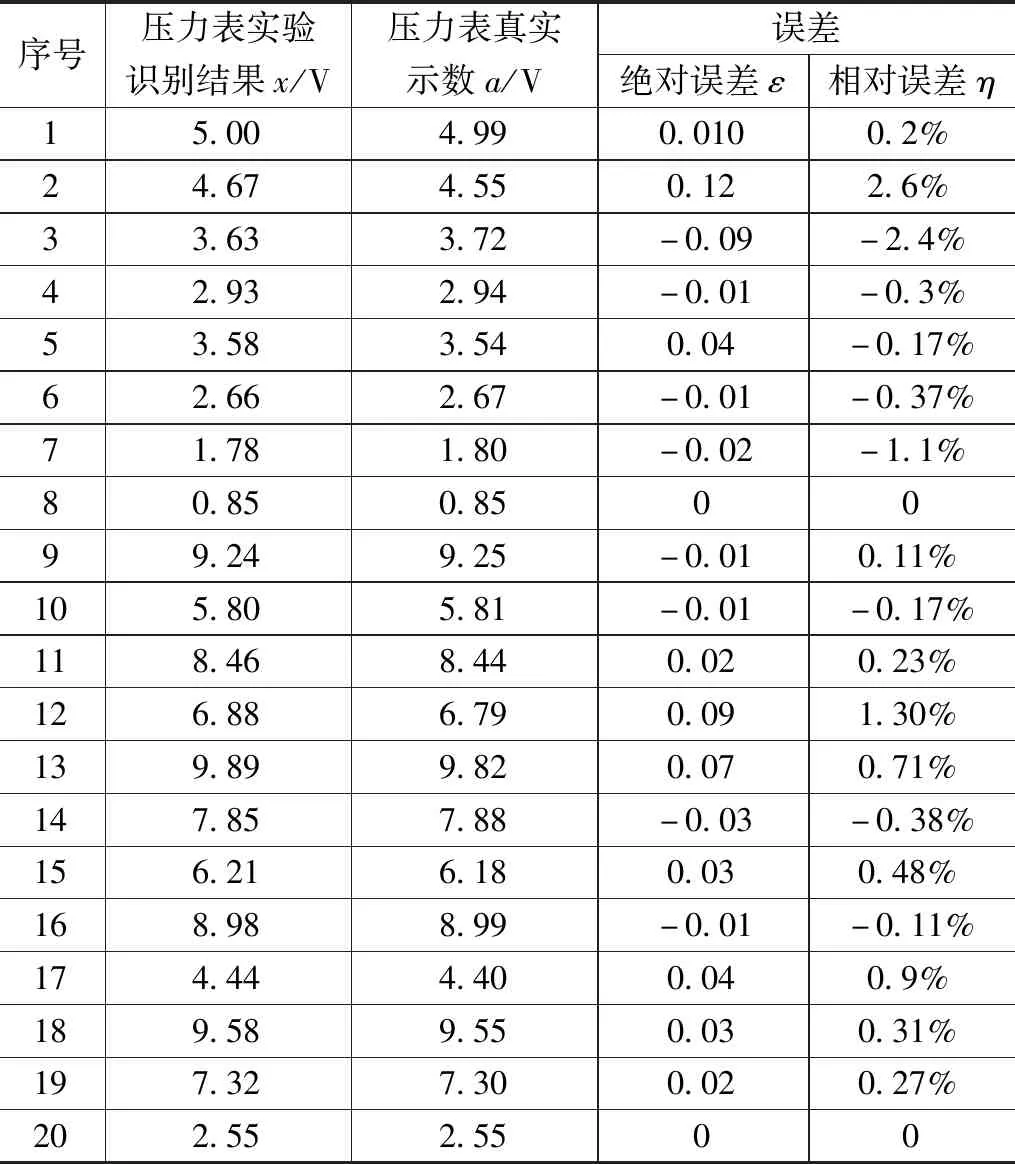
表3 仪表识别结果

绝对误差表达式见下式：

ε=x-a

(7)

相对误差表达式为下式：

(8)

由表3可以看出，本文论述的指针式仪表读数方法识别的指针读数绝对误差都在0.12 V以下，相对误差都在2.6%以下，该参数比较依赖真实数值a的大小，若真实电压值较小，那么相对误差很容易大。整体来看，仪表示数的读取准确率较高，能够正确的读取示数服务于站场的巡检工作。

5 结束语

本文提出了一种基于四足机器人作为载体运动控制，并通过深度强化学习(DQN)进行目标追踪任务和图像处理来读取仪表示数的新方法。首先通过改进的DQN算法的深度网络模型，根据仿真的环境中机器人学习效果，设计并调整动作奖励函数，设计机器人顶层决策控制系统。实现一维与二维状态参数输入下的仪表目标追踪任务。其次在仪表定位和仪表配准的基础上，通过K-means聚类二值化处理得到刻度分明的表盘；将图像进行内切圆处理，清除表盘以外的背景信息，降低图像数据量的同时保证图像质量，再在图像中间添加一根指针进行旋转，旋转过程中精确计算指针与表盘重合度最高的角度来得到对应刻度。

本文算法可实现运动过程中仪表目标的精准追踪和降低计算时间，并大大提高了仪表追踪与识别的精度和效率，为天然气站场的仪表安全监控提供了有效保障。